射频网课第三章学习(功率增益设计)

射频放大器功率增益设计：

引言：从"做什么"到"怎么做"

放大器的功率增益 是指放大器输出功率与输入功率的比值，用于衡量放大器对信号功率的放大能力。该指标通常以分贝（dB）为单位表示，计算公式如下：

GdB=10log⁡10(PoutPin)G_{dB} = 10 \log_{10} \left( \frac{P_{out}}{P_{in}} \right)GdB=10log10(PinPout)

其中，PoutP_{out}Pout 是输出功率，PinP_{in}Pin是输入功率。

这一章我们的目标就是对放大器的功率增益进行优化。具体来说，就是如何通过设计输入和输出匹配网络，来最大化放大器的功率增益 。

这部分内容将回答一个根本性问题：在琳琅满目的"增益"定义中，我们究竟要最大化哪一个？(优化谁)，也就是回答"是什么"和"为什么"

第一部分：明确设计变量与核心参数

在开始设计前，我们必须清晰地定义系统中所有重要的阻抗和反射系数点，并分清哪些是固定属性 ，哪些是可设计的变量 ，更重要的还有一点，方向性。

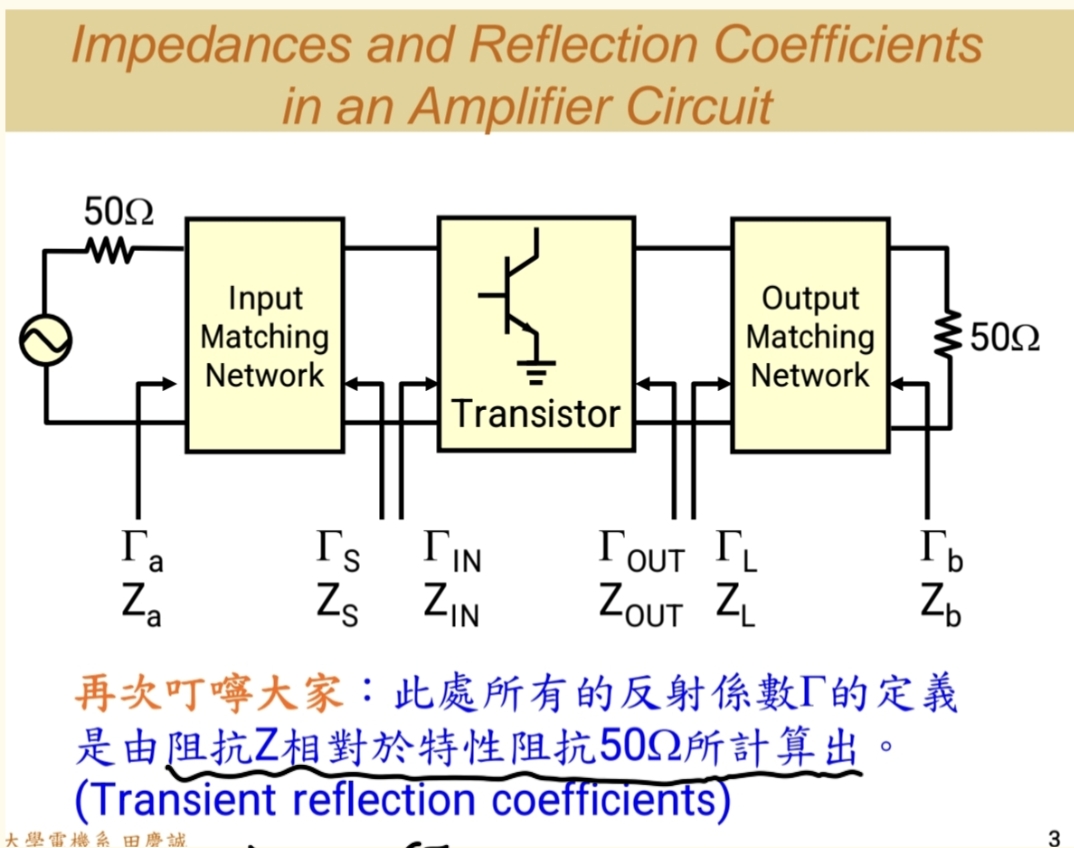
1.1 系统关键节点定义

ΓAΓ_AΓA(或 S11S_{11}S11of the entire amplifier)

定义：从整个放大器最左端 看进去的反射系数。它包含了输入匹配网络、晶体管、输出匹配网络和负载的所有影响。
计算基准 ：相对于50Ω。(为什么是50欧姆？ 这就像一个标准的计量单位（如"米"、"千克"），为了全世界的工程师能有统一的交流语言和测试基准，我们约定俗成地选择了50欧姆作为射频系统的特征阻抗。下面所有的参数也都是参照50Ω进行设计)
计算公式 ：假如从最左端看进去的负载，我们定义为ZaZ_{a}Za的话，ΓA=Za−50Za+50Γ_A = \frac{Z_{a} - 50}{Z_{a} +50}ΓA=Za+50Za−50

ΓSΓ_SΓS（s代表source的意思）

定义：从输入匹配网络的输出端 往左看，看向源方向（通常是一个50Ω的系统源）的反射系数。它包含了源阻抗和输入匹配网络的联合效应。
计算基准：相对于50Ω。
通过设计输入匹配网络 ，可以改变ΓSΓ_SΓS的值。

ΓinΓ_{in}Γin

定义：从晶体管的输入端 往右看进去的反射系数。它包含了晶体管自身、输出匹配网络和负载的所有影响。
计算基准：相对于50Ω。
常见误区 ：ΓinΓ_{in}Γin ≠ 晶体管的S11S_{11}S11 ,晶体管的S11S_{11}S11是在其输出端接50Ω时测得的。一旦输出端接了非50Ω的负载（输出匹配网络），ΓinΓ_{in}Γin就会变化。但两者是有关系的(后面还会进一步详细讲解)，具体公式为：

ΓinΓ_{in}Γin = S11S_{11}S11 + S12S21ΓL1−S22ΓL\frac{S_{12}S_{21}Γ_L}{1-S_{22}Γ_L}1−S22ΓLS12S21ΓL

这个公式体现了双向性效应(S12S_{12}S12) 的重要性。

ΓoutΓ_{out}Γout

定义：从晶体管的输出端 往左看进去的反射系数。它包含了晶体管自身、输入匹配网络和源的所有影响。
计算基准：相对于50Ω。
公式：

ΓoutΓ_{out}Γout = S22S₂₂S22 + S12S21ΓS1−S11ΓS\frac{S₁₂ S₂₁ Γ_S}{1 - S₁₁ Γ_S}1−S11ΓSS12S21ΓS

同样受双向性效应影响。

ΓLΓ_LΓL(L代表load,负载的意思)

定义：从输出匹配网络的输入端 往右看，看向负载方向（通常是50Ω的系统负载）的反射系数。它包含了负载阻抗和输出匹配网络的联合效应。
计算基准：相对于50Ω。
通过设计输出匹配网络 ，可以改变ΓLΓ_LΓL的值。

ΓbΓ_bΓb ( S22S_{22}S22 of the entire amplifier)

定义：从整个放大器最右端 看进去的反射系数。它包含了输出匹配网络、晶体管、输入匹配网络和源的所有影响。
计算基准：相对于50Ω。
重要性：这是网络分析仪在放大器输出端口实际测量到的S₂₂。

1.2 核心设计变量：ΓSΓ_SΓS 和 ΓLΓ_LΓL

从以上定义中，可以得出一个极其重要的结论：

在一个给定的晶体管（固定S参数）和固定的系统阻抗（50Ω）前提下，放大器所有其他节点的反射系数（ΓaΓ_aΓa, ΓinΓ_{in}Γin,ΓoutΓ_{out}Γout, ΓbΓ_bΓb）都是两个变量的函数，这两个变量就是：

源端(包含信号源，50Ω电阻，输入匹配网络)的反射系数 ΓsΓ_sΓs
负载端(包含输出匹配网络，50Ω电阻)的反射系数 ΓLΓ_LΓL

为什么？
ΓinΓ_{in}Γin 和 ΓoutΓ_{out}Γout 通过公式直接依赖于 ΓSΓ_SΓS 和 ΓLΓ_LΓL
ΓaΓ_aΓa 是从最左端看进去的，它必然受到右边一切电路的影响，而这些影响最终都通过 ΓinΓ_{in}Γin 和 ΓSΓ_SΓS 的相互作用体现出来。同理，ΓbΓ_bΓb 也依赖于 ΓLΓ_LΓL 和 ΓoutΓ_{out}Γout

因此，射频放大器的增益设计，本质上就是为给定的晶体管，寻找最优的 ΓSΓ_SΓS 和 ΓLΓ_LΓL 组合 ，使得我们想要的某种增益（通常是 Transducer Gain, GTG_TGT）达到最大。输入和输出匹配网络，就是实现我们计算出的最优 ΓSΓ_SΓS 和 ΓLΓ_LΓL 的物理电路。

第二部分：系统分析的通用语言------信号流图

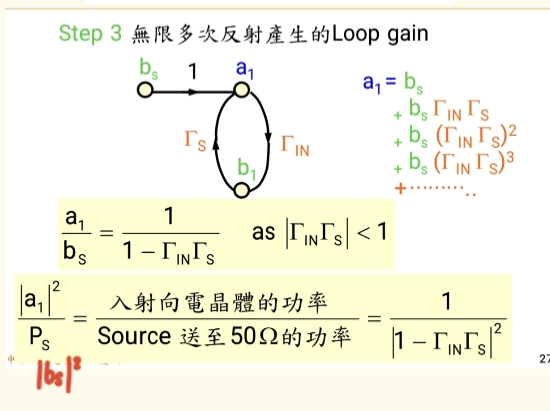
当我们有了这么多相互关联的反射系数和S参数时，如何系统地分析它们之间的功率流动？答案是使用信号流图 。这是射频领域一个非常强大且通用的工具，尤其适合于分析存在多次反射的复杂系统。

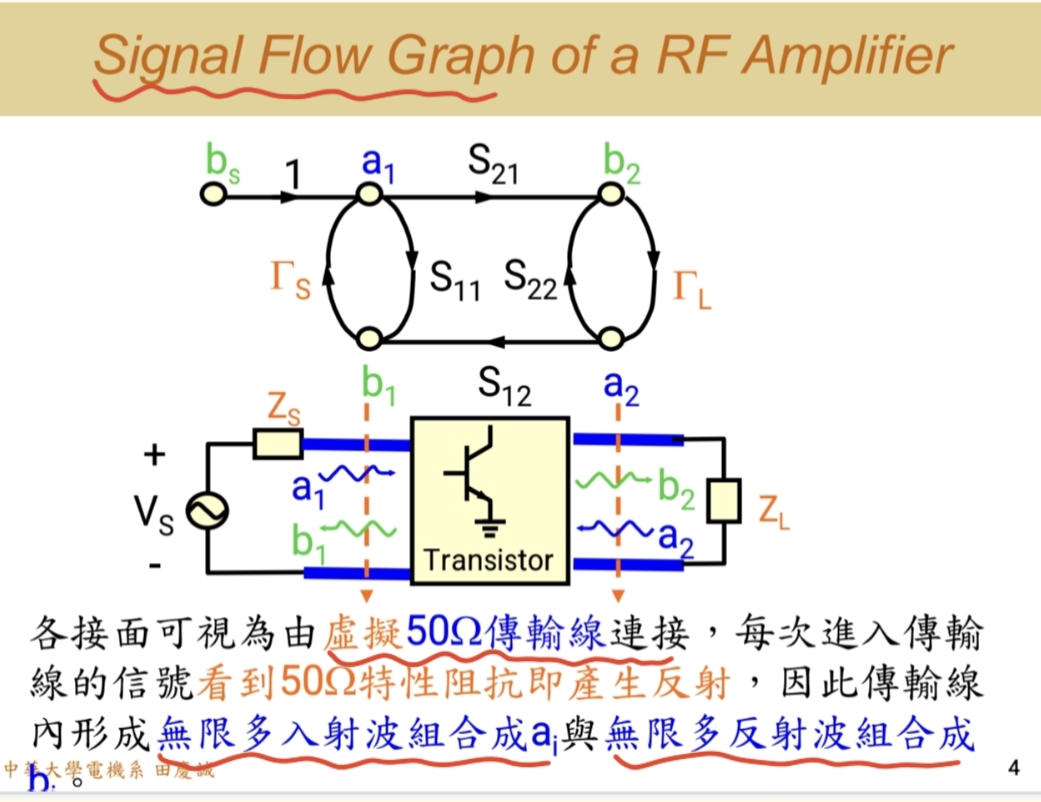
2.1 信号流图的基本规则

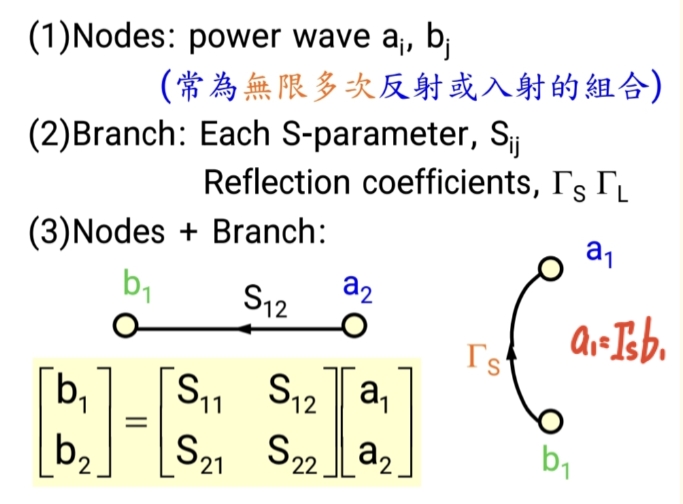
节点：代表功率波。分为两类：
- aiaᵢai：指向器件端口的入射波。
- bibᵢbi：从器件端口出来的反射波或输出波。
- 这里的aiaᵢai 和 bibᵢbi是稳态解 ，已经包含了系统中所有可能发生的无限多次反射叠加后的总效果。
支路：连接两个节点的有向线段，代表一种传输关系 ，上面标有系数。
- 系数可以是S参数 （如 S11,S21,S12,S22S₁₁, S₂₁, S₁₂, S₂₂S11,S21,S12,S22），表示信号通过晶体管的行为。
- 系数也可以是反射系数 （如 ΓS,ΓLΓ_S, Γ_LΓS,ΓL），表示信号在端口处的反射。
核心法则 ：进入一个节点的功率波，等于所有指向该节点的支路 的（来源节点功率波 × 支路系数）之和。

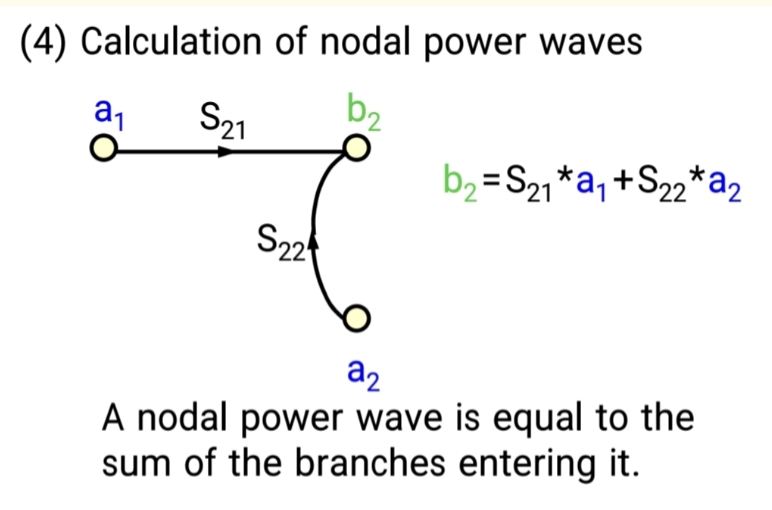
2.2 构建晶体管的信号流图

让我们根据S参数的定义来构建晶体管的信号流图。

S参数方程是：

b1=S11a1+S12a2b₁ = S₁₁ a₁ + S₁₂ a₂b1=S11a1+S12a2
b2=S21a1+S22a2b₂ = S₂₁ a₁ + S₂₂ a₂b2=S21a1+S22a2

根据法则，我们可以画出如下流图：

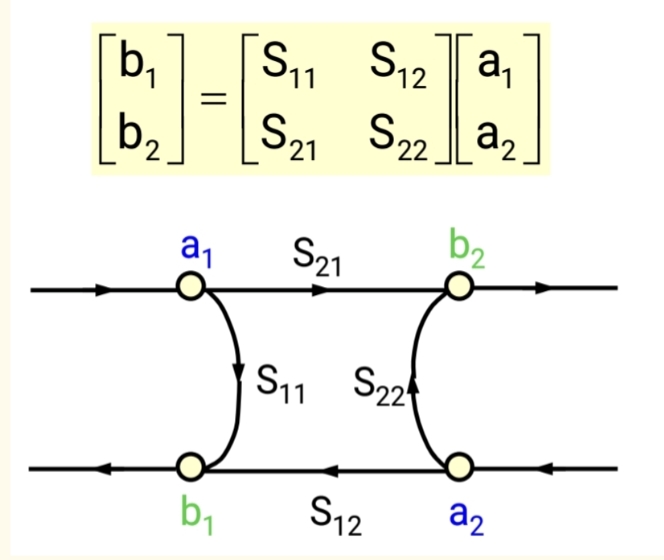
解读：

节点 b1b₁b1有两个来源：一是a1a₁a1经过 S11S₁₁S11 支路而来，二是 a2a₂a2 经过 S12S₁₂S12 支路而来。这正好对应 b1=S11a1+S12a2b₁ = S₁₁ a₁ + S₁₂ a₂b1=S11a1+S12a2。
节点b2b₂b2也有两个来源：一是a1a₁a1经过S21S₂₁S21支路而来，二是a2a₂a2经过 S22S₂₂S22支路而来。这正好对应 b2=S21a1+S22a2b₂ = S₂₁ a₁ + S₂₂ a₂b2=S21a1+S22a2。

这个流图完美地可视化了晶体管的双向性。

2.3 构建源和负载的信号流图

负载 (ΓLΓ_LΓL) ：比较简单。负载上的关系是：a2=ΓLb2a₂ = Γ_L b₂a2=ΓLb2。意思是"入射到负载的波 aaa₂，等于从负载反射回来的波 b2b₂b2 乘以负载的反射系数 ΓLΓ_LΓL"。所以在流图上，是一个从 b2b₂b2 指向 a2a₂a2 的支路，系数为 ΓLΓ_LΓL。
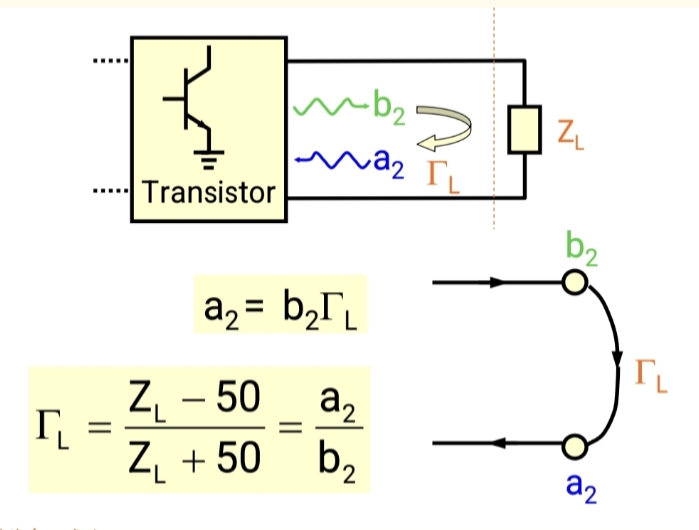
源 (含匹配网络) ：这是最难理解的部分。对于负载端 来说，有多少个入射波就有多少个反射波，这是一一对应的，但是源端并不是一一对应的关系.
- 我们定义一个量 bSb_SbS 。它的物理意义是：当源端完美匹配（没有反射）时，源能够发送到50Ω传输线中的入射波 。
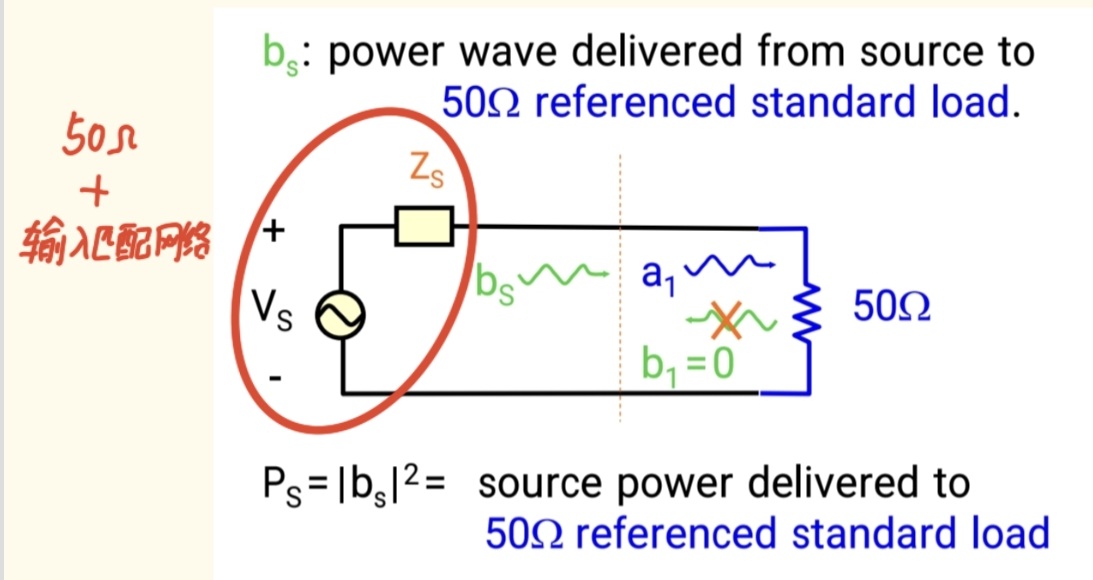
- 在实际系统中，源端存在反射 ΓSΓ_SΓS。那么，最终进入系统(晶体管)的总入射波 a1a₁a1 是多少呢？它由两部分组成：
  1. 源直接发出的波 bSb_SbS。
  2. 从系统(晶体管)反射回来的波 b1b₁b1，碰到源端后，再次被反射进系统，形成 ΓSb1Γ_S b₁ΓSb1。
- 因此，a1=bS+ΓSb1a₁ = b_S + Γ_S b₁a1=bS+ΓSb1。
- 在流图上，这表现为：一个独立的源节点 bSb_SbS，通过系数为1的支路指向 a1a₁a1；同时，从 b1b₁b1 有一个系数为 ΓSΓ_SΓS的支路指回 a1a₁a1。

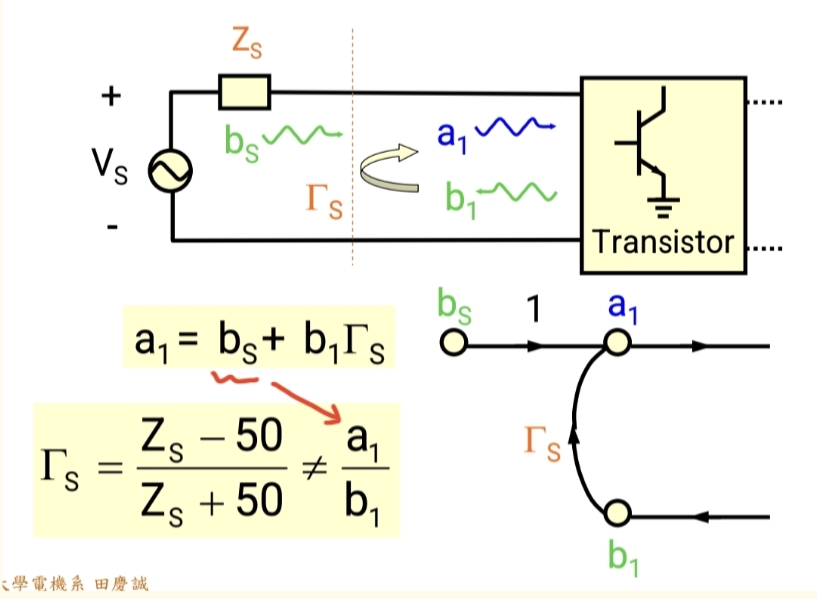
2.4 完整的系统信号流图

将晶体管、源、负载的流图连接起来，就得到了一个完整的、描述放大器功率流动的系统级流图：

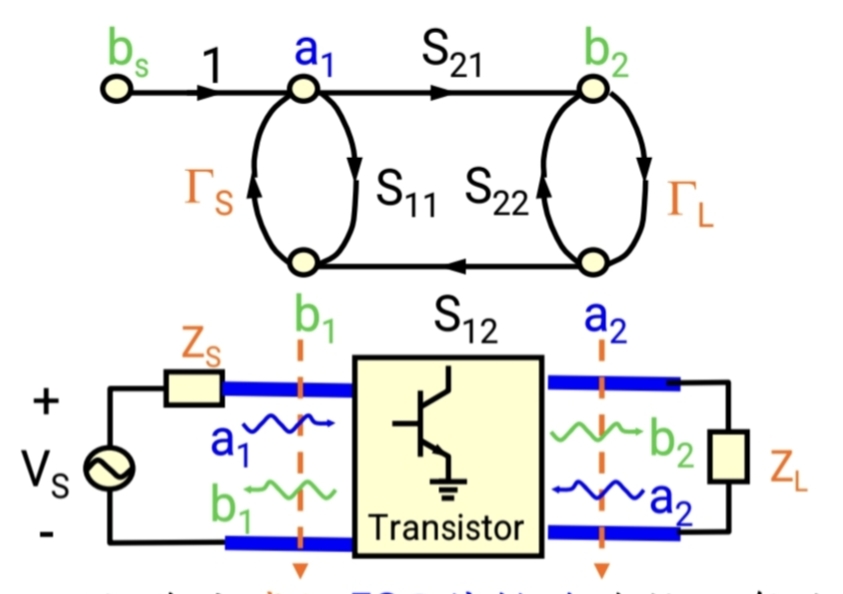
它清晰地展示了信号流动的所有路径
它解释了"稳态"值的由来 。a1,b1,a2,b2a₁, b₁, a₂, b₂a1,b1,a2,b2这些节点的值，是信号在图中所有路径中无限循环叠加后达到的稳定值。这比我们手动计算无限多次反射要方便得多。
它是数学分析的基础 。基于这个流图，我们可以直接推导出一些重要的公式，比如下面我们将要通过信号流图，推导出Γin\Gamma_\text{in}Γin的计算公式:
Γin\Gamma_\text{in}Γin表示输入端稳态下的总反射系数，包含无限多次反射的叠加结果。其核心公式是输入端的反射波b1b_1b1与入射波a1a_1a1的比值：
Γin=b1a1 \Gamma_\text{in} = \frac{b_1}{a_1} Γin=a1b1
a1a_1a1：仅包含一次入射信号（从50Ω电缆输入）。
b1b_1b1：从信号流图中我们可以清晰的看出，从共有两个来源，一是直接反射S11S_{11}S11(直接反射项)，二是经过负载多次反射后返回的叠加信号 。

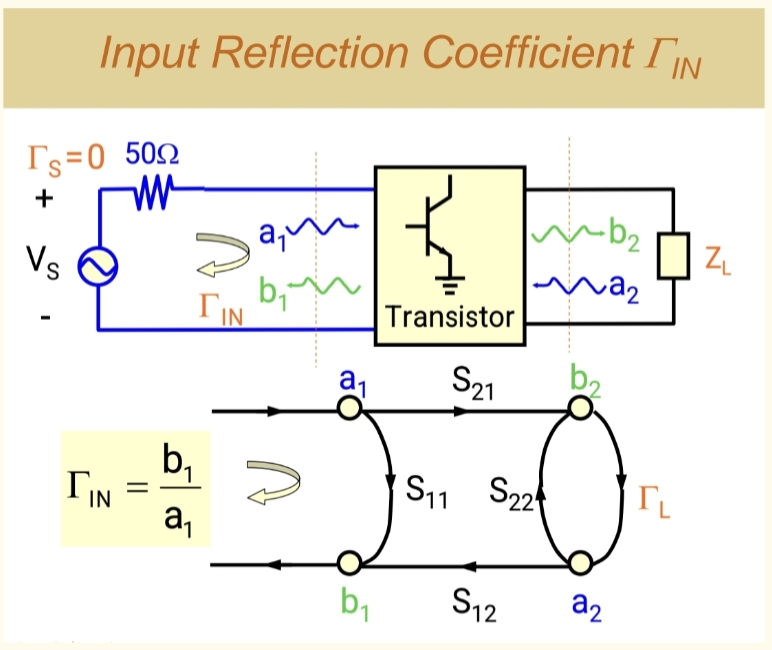
信号通过晶体管正向增益S21S_{21}S21到达负载ΓL\Gamma_LΓL，再通过反向隔离S12S_{12}S12返回输入端。

而通过信号流图不难看出，在a2a_2a2节点时，信号可以绕一圈，甚至绕几圈回路才回去，每次绕行负载回路时，都会额外引入回路增益（公比）：
公比=S22ΓL \text{公比} = S_{22} \Gamma_L 公比=S22ΓL

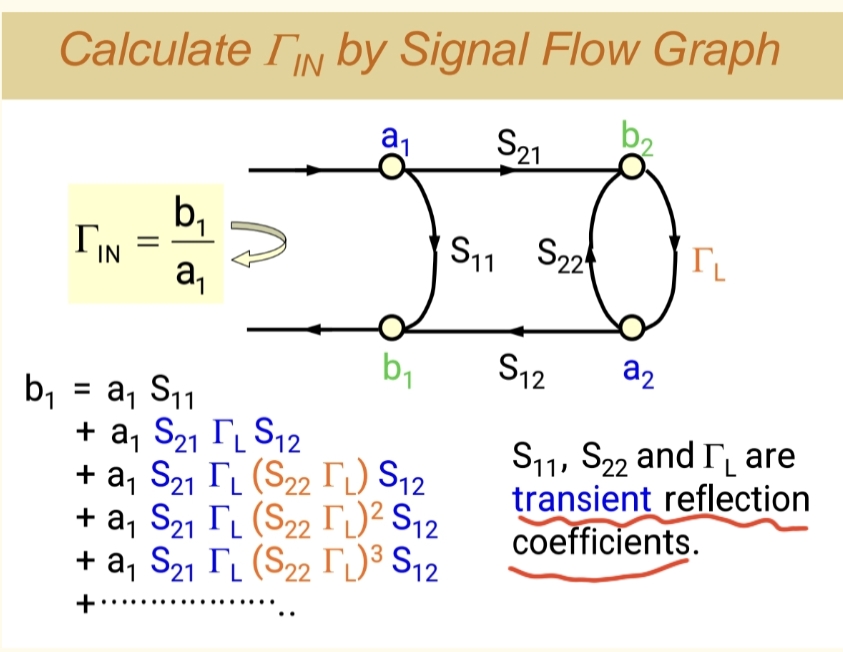
于是我们通过等比级数求和公式不难得到:
Γin=S11+S21ΓLS121−S22ΓL \Gamma_\text{in} = S_{11} + \frac{S_{21} \Gamma_L S_{12}}{1 - S_{22} \Gamma_L} Γin=S11+1−S22ΓLS21ΓLS12

注意事项

1.单行道假设：信号从输入端进入后，仅能通过负载回路反射，不能逆向返回。

2.稳态条件：公比需满足∣S22ΓL∣<1|S_{22} \Gamma_L| < 1∣S22ΓL∣<1，否则级数发散（物理上系统不稳定，也就是会发生振荡 ）。

3.负载影响：输入阻抗受负载匹配（ΓL\Gamma_LΓL）影响，即使S12S_{12}S12较小也不可忽略，我们把S12=0S_{12} = 0S12=0的元件称之为单向元件 ，反之，称为双向元件 。

具体我们来讨论下面两种情况:

1.双向元件的匹配:

即使通过匹配电路使S11S_{11}S11=0，若后级负载ΓLΓ_LΓL≠0，前端的Γin\Gamma_{in}Γin将受反向传输参数S12S_{12}S12影响而失配。此时匹配仅在后级为50欧姆时成立，后级调整会破坏前级匹配状态 。

2.单向元件的匹配:

当电晶体为单向器件S12S_{12}S12=0，逆向增益为零，ΓinΓ_{in}Γin公式简化为：
Γin=S11Γ_{in} = S_{11}Γin=S11

此时前级匹配S11S_{11}S11=0不受后级负载变化影响，ΓinΓ_{in}Γin恒为0。实际设计中需验证S12S_{12}S12是否可忽略以简化匹配。

2.5 隔离度

但现实中，晶体管并非绝对是一个单向型或者是一个双向型的元件，更多时候，应该处于两者之间，那我们如何衡量一个晶体管前后级的隔离程度 呢？于是我们定义了一个叫做隔离度的参数.

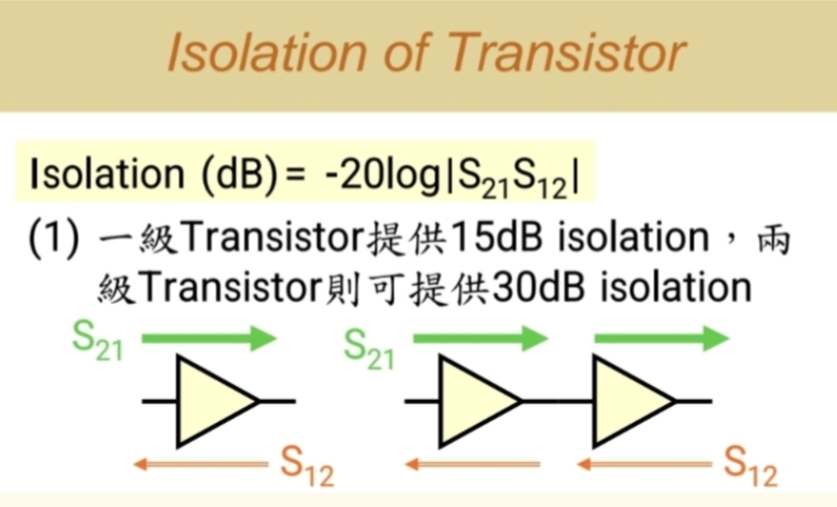
隔离度的定义与目的
目的：防止信号从输出端反射回输入端，确保信号单向传输。
定义：在最坏情况（全反射）下，衡量信号从输出端泄漏回输入端的程度。隔离度越好，泄漏回来的信号越少。
隔离度的量化与计算
核心参数 ：使用S参数进行量化。
S21S_{21}S21：表示正向传输增益（信号"过去"）。
S12S_{12}S12：表示反向传输增益（信号"回来"）。
计算公式 ：Isolation=−20log(Isolation = -20log(Isolation=−20log(S21S_{21}S21× S12S_{12}S12) (S参数为电压参数，所以为20log,为保证隔离度是一个正数，因此前面加上一个负号)
理解：该公式计算的是在全反射的最坏情况下，泄漏回来的信号总损耗。值越大，代表隔离效果越好。
级联系统的隔离度
当两级相同的电路级联时，总隔离度会增加,如果单级隔离度为X dB，则两级级联后的隔离度近似为 2X dB。这是因为信号需要经过两次"过去"和两次"回来"的衰减，数值相乘，在dB值上表现为相加。
实现隔离的两种常见电路
缓冲级：利用晶体管本身的单向性提供隔离。
衰减器：由三个电阻构成的T型或π型网络，通过引入固定的信号损耗来改善阻抗匹配，从而实现隔离。
隔离度的主要应用场景
减少振荡器的负载牵引效应 ：负载变化会改变振荡器的谐振频率，导致频率不稳定。
解决方案 ：在振荡器和负载之间加入缓冲放大器。放大器允许信号单向通过，但能阻止负载反射回来的信号影响振荡器，从而稳定频率。

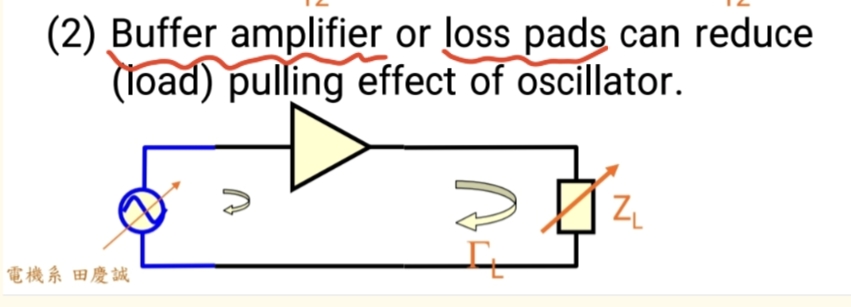
改善混频器的电压驻波比 ：混频器的输入端口VSWR较差（如VSWR=4），会导致其前级放大器工作异常。

解决方案：在放大器和混频器之间插入一个衰减器。衰减器通过两次衰减（正向信号和反射信号）来降低有效的反射系数，从而改善系统整体的VSWR。但这需要以牺牲增益（功率）为代价 。

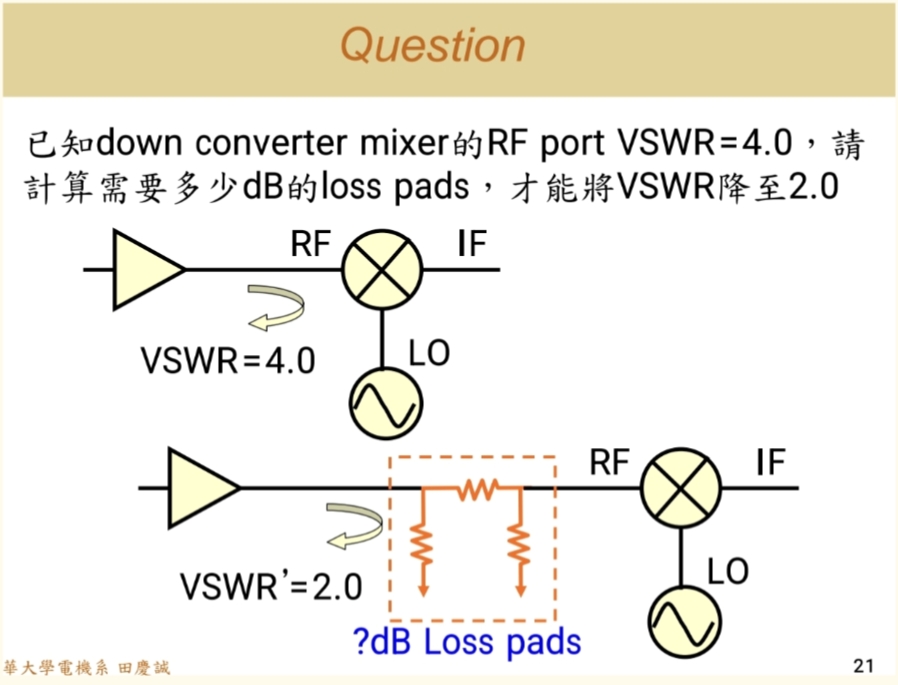
简化计算示例 ：将不良VSWR（4）对应的反射系数dB值，与目标VSWR（2）对应的反射系数dB值相减，估算出所需衰减器的衰减量（如~2.55 dB）。提示： 问题中提供的衰减器计算方法是一种简化的粗略估算 ，因为它忽略了相位的影响。在实际工程中，最终设计必须使用网络分析仪 或仿真软件 进行验证和优化。

第三部分：不匹配因子 (Mismatch Factor) M

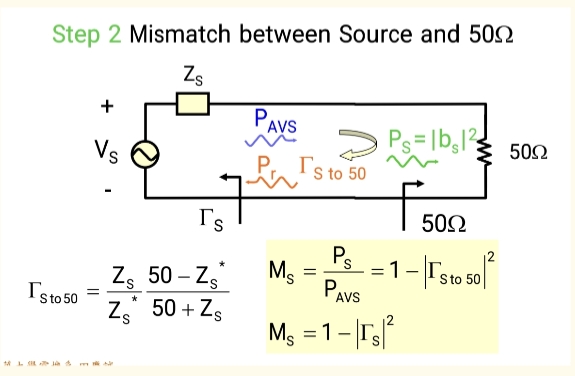
在我们讨论如何让放大器获得高增益之前，必须首先回答一个更根本的问题：当任意两个复数阻抗 直接相连时，它们之间的最大可能功率传输效率 是多少？这个问题的答案就是不匹配因子 M 。它是理解后续所有增益和匹配概念的基石。

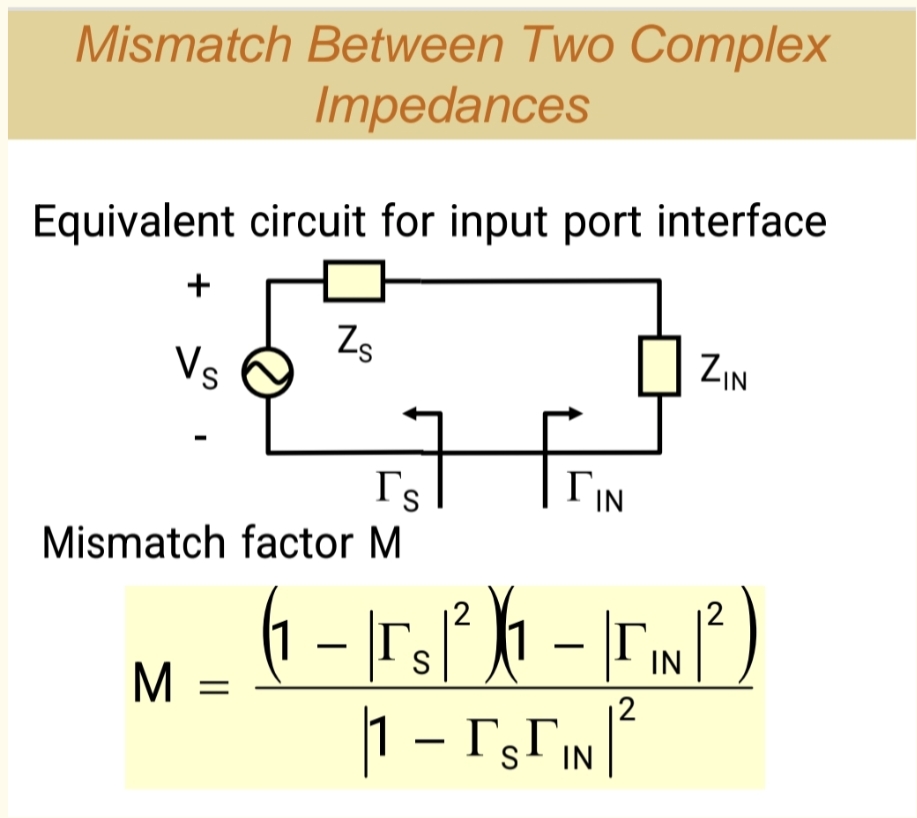
3.1 M 因子的物理场景

考虑一个具有内阻抗 ZSZ_SZS（反射系数为 ΓS\Gamma_SΓS）的源，直接连接到一个负载阻抗 ZINZ_{IN}ZIN（反射系数为 ΓIN\Gamma_{IN}ΓIN）。需要注意的是，ΓS\Gamma_SΓS 和 ΓIN\Gamma_{IN}ΓIN 都是相对于同一个参考阻抗如50Ω)来定义的 。

不匹配因子 M 的精确定义是：实际送达负载的功率 与 如果源和负载是共轭匹配时所能送达的最大功率 的比值。它的公式是：
M=(1−∣ΓS∣2)(1−∣ΓIN∣2)∣1−ΓSΓIN∣2M = \frac{(1 - |\Gamma_S|^2)(1 - |\Gamma_{IN}|^2)}{|1 - \Gamma_S \Gamma_{IN}|^2}M=∣1−ΓSΓIN∣2(1−∣ΓS∣2)(1−∣ΓIN∣2)

3.2 公式的深度分解：三个关键物理效应

这个看似复杂的公式，可以完美地分解为三个连续的物理过程：

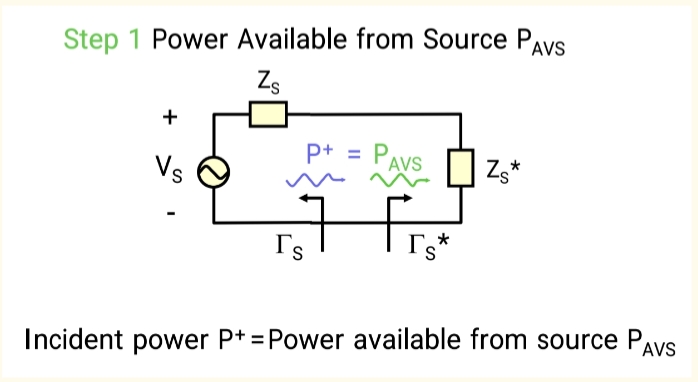
源端失配损耗MsM_ sMs ：(1 - ∣ΓS∣2|\Gamma_S|^2∣ΓS∣2)
- 意义：这代表了由于源阻抗 (ZSZ_SZS) 不等于系统参考阻抗（50Ω）而造成的初始损耗。它描述了源"激发"信号到传输系统中的能力。即使负载完美匹配到50Ω，这部分功率也因为源自身的不匹配而无法被有效送出。
- 比喻：就像一个水压不足的水泵（源不匹配），即使水管（传输线）和水桶（负载）都很完美，初始的出水量就已经受限了。
环路增益：(1∣1−ΓSΓIN∣2\frac{1}{|1 - \Gamma_S \Gamma_{IN}|^2}∣1−ΓSΓIN∣21)
- 意义：这是最精妙、最核心 的部分。它描述了信号在源和负载之间无限次反射后产生的净效应。
- 推导过程:晶体管并非可以直接完全等效于负载，入射波a1除了等于源端发射来的bsb_sbs之外，bsb_sbs也会在晶体管内部反射回来，经过源端反射后，又重新入射回负载(晶体管)，而这个过程可以循环很多次，最终得到的依旧是一个无穷等比级数
- 建设性干涉 ：当 ΓSΓIN\Gamma_S \Gamma_{IN}ΓSΓIN 的相位为 0°0°0°（一个正实数）时，分母 ∣1−ΓSΓIN∣2|1 - \Gamma_S \Gamma_{IN}|^2∣1−ΓSΓIN∣2 小于 111。这意味着多次反射的信号在负载端同相叠加，反而提升了总的传输效率，使得 MMM 大于前两个因子的简单乘积。
  破坏性干涉 ：当 ΓSΓIN\Gamma_S \Gamma_{IN}ΓSΓIN 的相位为 180°180°180°（一个负实数）时，分母 ∣1−ΓSΓIN∣2|1 - \Gamma_S \Gamma_{IN}|^2∣1−ΓSΓIN∣2 大于 111。这意味着多次反射的信号在负载端反相抵消，降低了总的传输效率，使得 MMM 小于前两个因子的简单乘积。
- 比喻：在两个镜子（源和负载）之间来回反射的光线。如果镜子的曲率和距离正好，光会相互增强（建设性干涉，房间更亮）；如果不对，光就会相互抵消（破坏性干涉，房间变暗）。
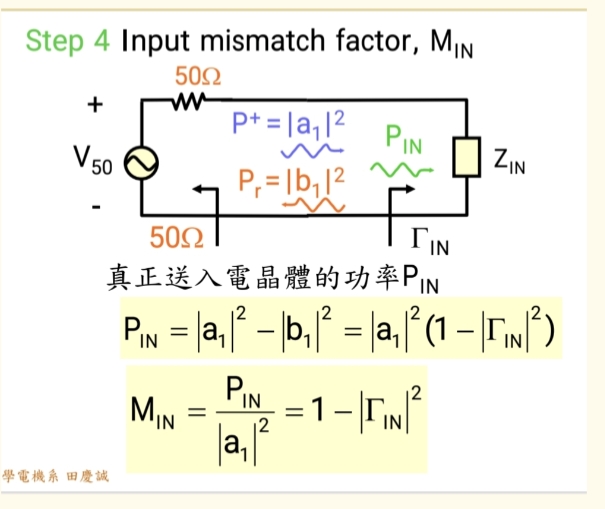
负载端失配损耗MinM_ {in}Min ：(1 - ∣ΓIN∣2)|\Gamma_{IN}|^2)∣ΓIN∣2)
- 意义：这代表了由于负载阻抗(ZIN)(Z_{IN})(ZIN) 不等于系统参考阻抗（50Ω）而造成的终端损耗。它描述了负载"吸收"来自传输系统信号的能力。即使源完美匹配到50Ω，送到负载的能量也会因为负载不匹配而被反射掉一部分。
- 比喻：就像一个形状很奇特的水桶（负载不匹配），即使水泵和水管都很完美（供水没有问题），我们也无法有效地接住所有来的水，总有一些水洒出去。
最后不匹配因子M就等于上述三个因子的乘积

3.3 验证共轭匹配时，M=1

让我们用这个万能的公式来验证射频设计的黄金法则：共轭匹配。

当实现共轭匹配时，即 (ZIN=ZS∗Z_{IN} = Z_S^*ZIN=ZS∗)，对应的反射系数关系为 (ΓIN=ΓS∗\Gamma_{IN} = \Gamma_S^*ΓIN=ΓS∗)。

我们将 (ΓIN\Gamma_{IN}ΓIN = ΓS∗\Gamma_S^*ΓS∗) 代入 M 的公式：

M = (1−∣ΓS∣2)(1−∣ΓS∗∣2)∣1−ΓSΓS∗∣2\\frac{(1 - \|\\Gamma_S\|\^2)(1 - \|\\Gamma_S\^\*\|\^2)}{\|1 - \\Gamma_S \\Gamma_S\^\*\|\^2}∣1−ΓSΓS∗∣2(1−∣ΓS∣2)(1−∣ΓS∗∣2)

M = (1−∣ΓS∣2)2∣1−∣ΓS∣2∣2\\frac{(1 - \|\\Gamma_S\|\^2)\^2}{\|1 - \|\\Gamma_S\|\^2\|\^2}∣1−∣ΓS∣2∣2(1−∣ΓS∣2)2

因为 (1−∣ΓS∣2)(1 - |\Gamma_S|^2)(1−∣ΓS∣2) 是正实数，所以绝对值等于自身：

M = (1−∣ΓS∣2)2(1−∣ΓS∣2)2=1\\frac{(1 - \|\\Gamma_S\|\^2)\^2}{(1 - \|\\Gamma_S\|\^2)\^2} = 1(1−∣ΓS∣2)2(1−∣ΓS∣2)2=1

结论：在共轭匹配时，不匹配因子 M = 1。这意味着尽管源和负载本身都可能不匹配于50Ω，但由于它们彼此之间是"完美搭档（共轭转置）"，它们之间的功率传输效率达到了理论最大值100%。所有的初始失配和干涉效应被完美地补偿了。这完美地证明了我们一直追求的"共轭匹配"目标的正确性

3.4 例题

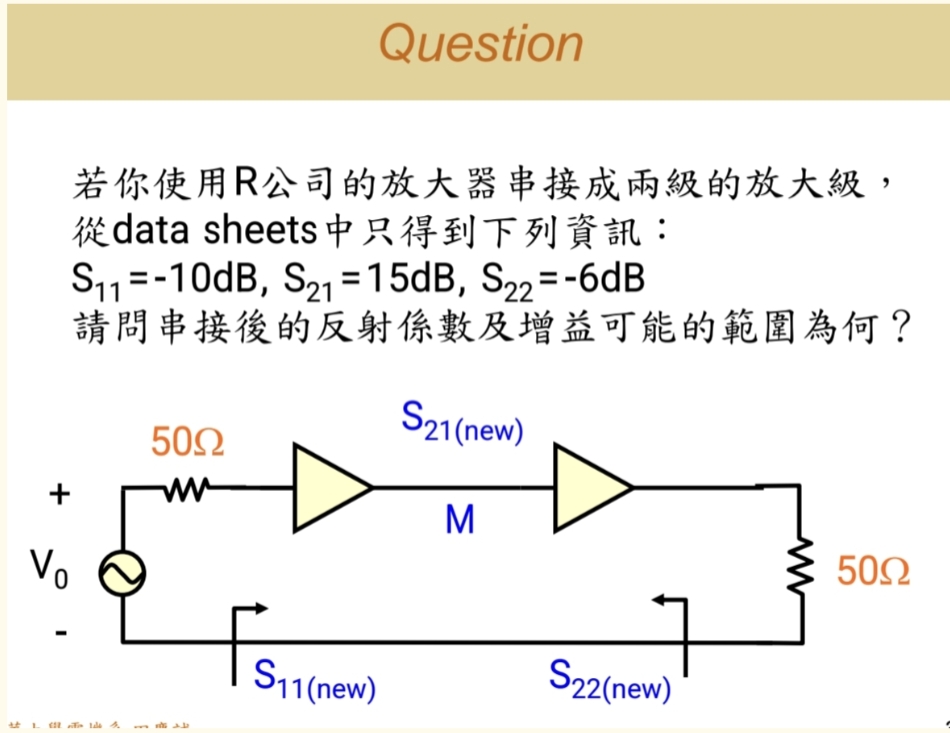
首先，我们假设晶体管的 S₁₂ 反向传输系数为零，即采用单向化模型。基于这个假设，信号反馈路径被切断，这能够大大简化分析。

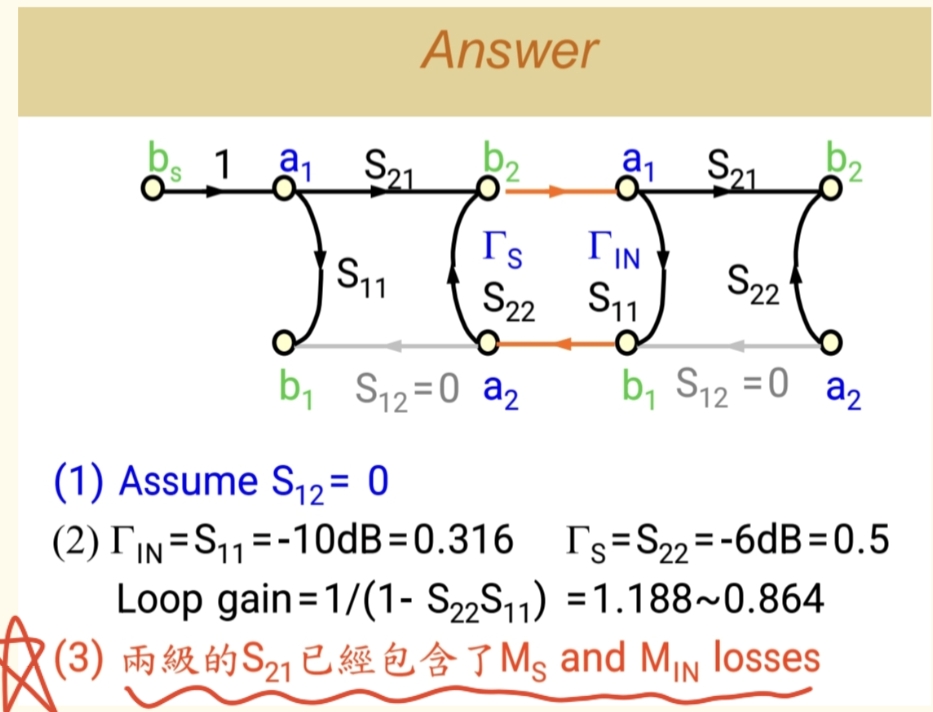
1.输入反射系数 (ΓinΓ_{in}Γin) ：当输出端完美匹配（接50欧姆负载）时，从输入端看进去的反射系数就是放大器自身的 S₁₁。因为负载无反射回来，单向元件（S₁₂= 0），信号不会从输出端反射回来影响输入。因此，ΓinΓ_{in}Γin = S₁₁ 。
输出反射系数 (ΓSΓ_{S}ΓS) ：同理，当输入端完美匹配（接50欧姆源）时，从输出端看进去的反射系数就是放大器自身的 S₂₂。因为假设 S₁₂ = 0，信号无法从输入端反馈回来。因此，ΓSΓ_{S}ΓS = S₂₂ 。根据给定参数换算成线性值：S₁₁ = 0.316，S₂₂ = 0.501

2.当两级放大器串联时，第一级的输出（由 S₂₂ 表征）连接到第二级的输入（由 S₁₁ 表征）。这会形成一个潜在的反射环路，其 环路增益 为 S₂₂ × S₁₁。这个环路增益的大小取决于 S₂₂ 和 S₁₁ 的相位关系：- 建设性干涉 ：当相位相加为0°时，信号正向叠加，可能使总体增益增大。- 破坏性干涉 ：当相位相反为180°时，信号相互抵消，可能导致总体增益减小。因此，环路增益 1 / (1 - S₂₂ × S₁₁) 是一个变量，它会放大或衰减级联系统的总增益。

关键概念：S₂₁ 已包含失配损耗在计算级联总增益时，一个至关重要且容易出错的概念是：单个放大器的 S₂₁ 是在输入端接50欧姆源、输出端接50欧姆负载 的标准条件下测得的。这个测量值已经计入了该放大器自身的 S₁₁（输入失配）和 S₂₂（输出失配）在标准环境下的净效应。因此，当我们使用 S₂₁进行计算时：- 不需要也不应该 再为每一级单独计算源失配因子 (MSM_SMS) 或负载失配因子 (MLM_LML)。- 这些失配影响已经隐含在各自的 S₂₁ 数值之中 。我们唯一需要额外考虑的，是两级连接时新产生 的失配，即由前述环路增益 所表征的效应。
因此，两级放大器总增益（线性值）的完整计算公式为：GtotalG_{total}Gtotal = |S₂₁|² × |环路增益效应| × |S₂₁|²代入数值并进行计算，在考虑环路增益的波动后，总增益的可能范围大约在 28.73dB 到 31.5 dB 之间 。这与简单将两级增益相加（15 dB + 15 dB = 30 dB）相比，存在约 ±1.5 dB 的误差 ，这个误差完全是由两级间的环路增益（多次反射）造成的。

5.当单个放大器的 S₁₁ 或 S₂₂ 很差（即反射系数模值很大）时，级联后的环路增益效应会非常显著。其影响是增强还是削弱，取决于无法预知的相位，这会带来很大的不确定性。- 最佳情况 ：如果两个放大器本身的 S₁₁ 和 S₂₂ 都非常小（即匹配良好），那么环路增益效应接近于1，可以忽略不计。此时，总增益就近似等于两级 S₂₁ (dB值) 的简单相加。在极端情况下，如果相位导致180°的破坏性干涉，即便两级放大器本身性能很好，总增益也可能会意外地下降多达3 dB 。

Ps:我们的整个分析基于 S₁₂ = 0 的假设。在实际应用中，S₁₂ 并不为零，因此实际情况会更复杂。要获得精确结果，必须使用完整的S参数并进行详细仿真。

【第三部分小结与衔接】
不匹配因子 M 是我们整个性能分析大厦的基石。 它告诉我们，两个阻抗之间的功率传输，不是简单的"1-反射功率"，而是一个包含初始损耗和复杂干涉效应的动态过程。我们的终极目标，是通过设计使得 M=1。现在，我们拥有了M这个强大的分析工具，就可以开始用它来构建和理解射频放大器最核心的性能指标------功率增益(Gain)。

第四部分：核心性能------深入理解功率增益 (Gain)

放大器，顾名思义，它最重要的功能就是放大，那你做的放大器和我做的放大器，哪个更好呢？如何刻画放大器放大的本领？于是我们用增益来刻画。所以，增益是我们追求的第一个核心性能指标。而基于对 M 因子的理解，我们就能深刻洞察各种增益定义的由来和意义。

4.1 为什么增益定义不止一种？

你可能会疑惑，增益不就是输出功率除以输入功率吗？在射频领域，事情没那么简单。原因主要有两个，一是因为存在不匹配 ，由于不匹配，所以"输入"到底是什么，"输出"是什么，就有了不同的定义，进而引出了几种不同的增益定义。二是我们设计的目标不同 ，我们需要不同的增益，来适用于不同场景。当然，本质上我们所有的这些定义，都是在衡量不同节点之间的 M 因子的组合。

4.2 不同功率定义

我们先来看第一个问题，究竟会有哪些输入，和有哪些输出，明确几个核心的功率定义，这是理解所有增益计算的基础：
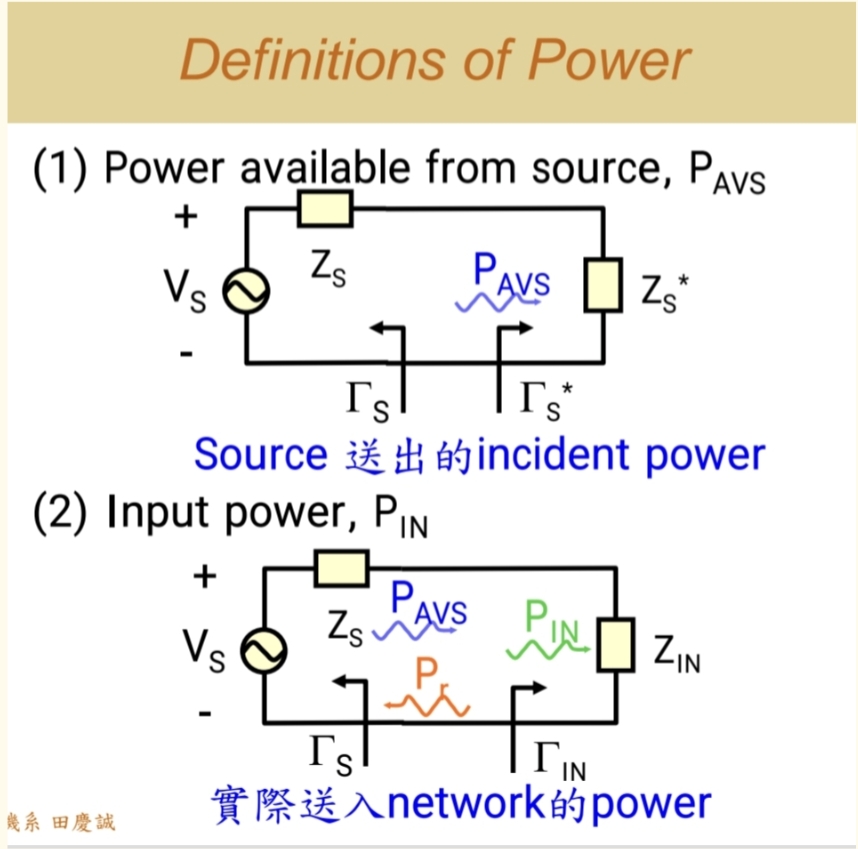
PAVSP_{AVS}PAVS 源可用功率：当源端实现共轭匹配时，它能送出的最大入射功率(incident power)。这代表了源的潜力。
PINP_{IN}PIN - 输入功率：信号源实际送入放大器输入端的功率。由于输入失配 ，它等于入射功率减去反射功率，因此 PINP_{IN}PIN ≤ PAVSP_{AVS}PAVS。

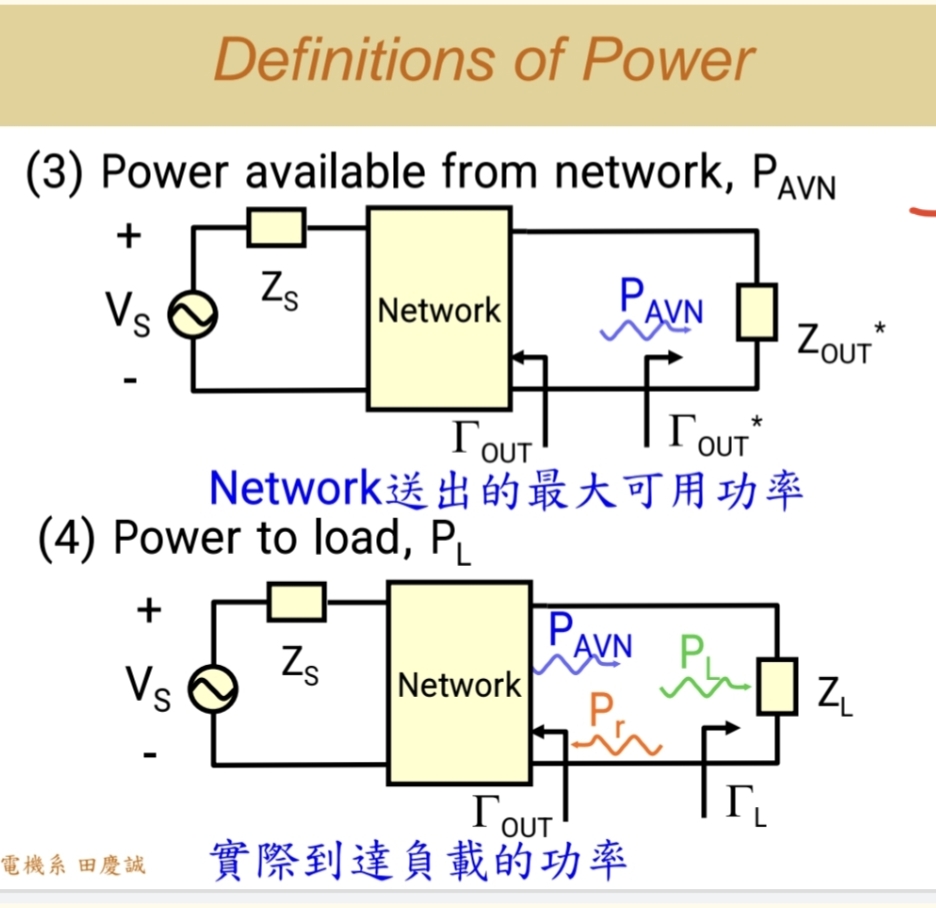
PAVNP_{AVN}PAVN - 网络可用功率：当放大器输出端实现共轭匹配时，它能送出的最大功率。这代表了放大器的输出潜力。
PLP_{L}PL - 负载功率：放大器实际送入负载的功率。由于输出失配，PLP_{L}PL ≤ PAVNP_{AVN}PAVN。

4.3 不同增益定义

有了功率定义后，我们就可以来定义不同的增益，值得再次强调，失配与否是推导这些计算公式的根本由来，而定义不同增益的目的，是为了适用于不同的场景。

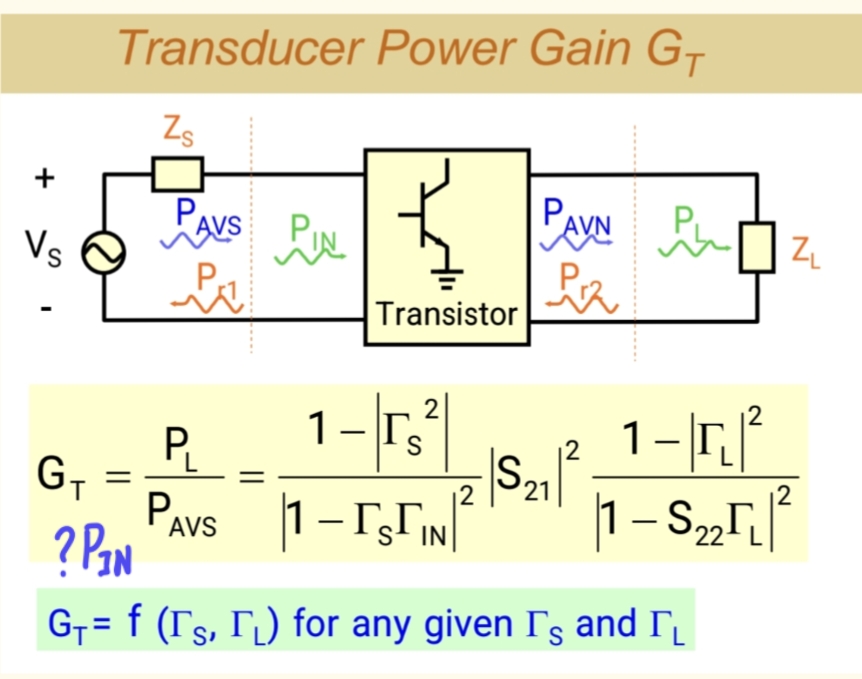
转换功率增益 (Transducer Power Gain, (GTG_TGT))
- 定义 : ( GT=PLPavsG_T = \frac{P_L}{P_{avs}}GT=PavsPL)
  - (PLP_LPL)：实际送达负载的功率。
  - (PAVSP_{AVS}PAVS)：源能够提供的最大可用功率。
- 为什么增益定义为 PL/PAVSP_L /P_{AVS}PL/PAVS，而不是 PL/PINP_L / P_{IN}PL/PIN？
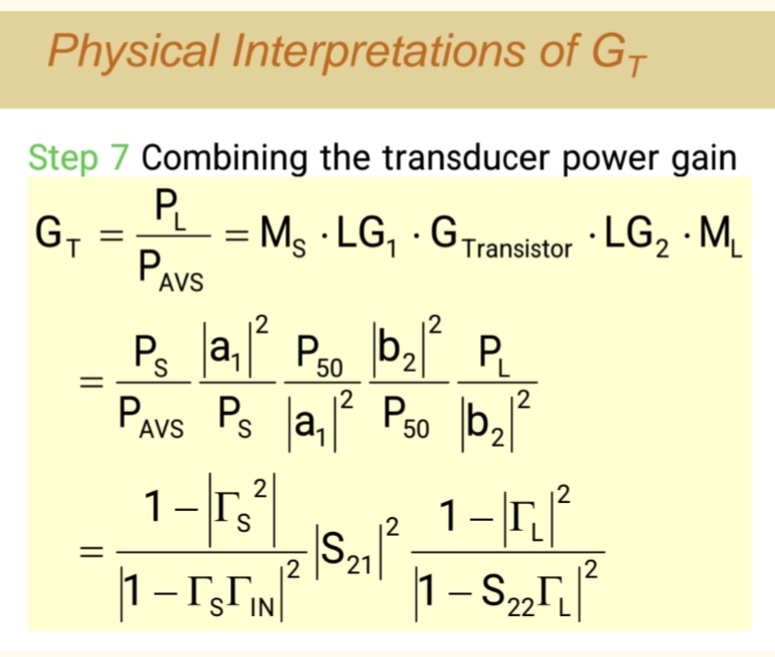
  因为在S参数体系（包括网络分析仪）中，增益的参考基准是入射功率(a₁)，而非实际进入网络的功率。PINP_{IN}PIN是入射功率减去反射功率，如果用PINP_{IN}PIN作分母，就等于让放大器为前级的失配"背锅"，这会虚高增益值。失配的责任应归于系统设计，而非放大器本身。
- 计算公式总共分为五大核心：GT=MS×LoopGain1×∣Gtransistor∣2×LoopGain2×MLG_T = M_S × Loop Gain_1 × |G_{transistor}|² × Loop Gain_2×M_LGT=MS×LoopGain1×∣Gtransistor∣2×LoopGain2×ML

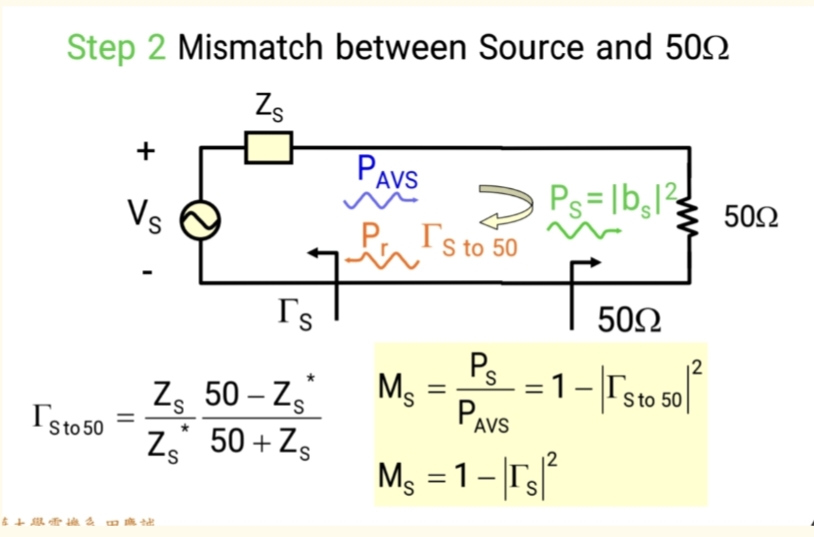
源失配损耗MSM_SMS

源试图把它的最大可用功率(PavsP_{avs}Pavs)送出去。但由于源自身的阻抗((ZSZ_SZS))和50欧姆传输线不匹配，会产生反射。一部分功率在出发时就被浪费了。
数学因子 : (1−∣ΓS∣21 - |\Gamma_S|^21−∣ΓS∣2) (这正是M因子公式中的源失配项)
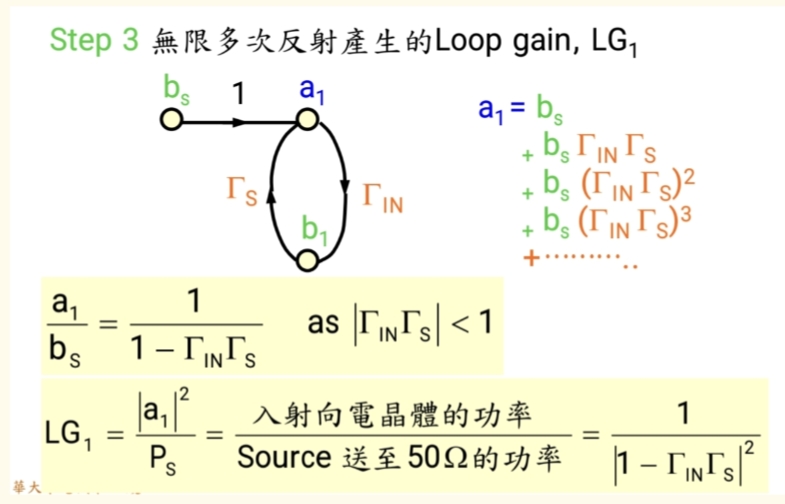
输入环路干涉Loop Gain_1
- 成功进入传输线的信号到达放大器输入端。由于输入端也不是完美匹配(ΓinΓ_{in}Γin ≠ 0)，一部分信号被反射回源端。源端又会再次反射这部分信号... 如此往复，形成无限次反射。这些反射波在输入端叠加，可能增强也可能削弱最终的入射信号。
- 数学因子 : ( 1∣1−ΓinΓS∣2\frac{1}{|1 - \Gamma_{in}\Gamma_S|^2}∣1−ΓinΓS∣21) (这正是M因子公式中的干涉效应项，与源失配项结合，构成了源与放大器输入端之间的完整M因子)
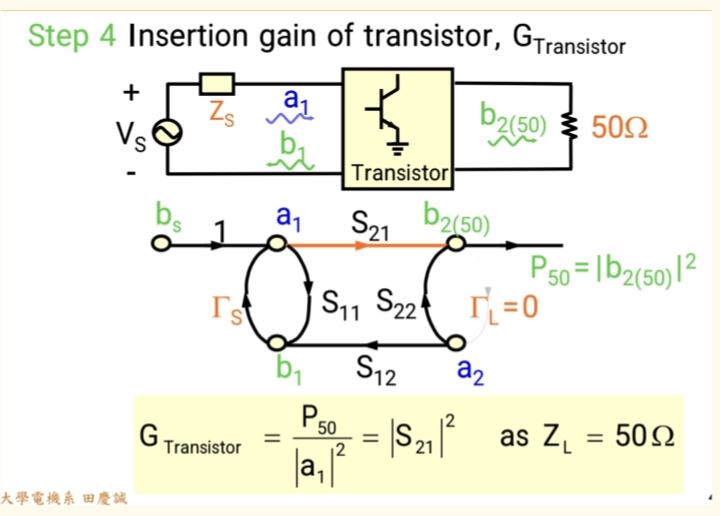
晶体管本征放大∣Gtransistor∣2|G_{transistor}|²∣Gtransistor∣2
- 最终在输入端稳定下来的入射波，进入晶体管的核心，被其放大。这是放大器的"本职工作"。
- 数学因子 : ( ∣S21∣2|S_{21}|^2∣S21∣2 ) (注意：这个在50Ω系统下测得的S₂₁，本身已经包含了在标准测试环境下输入输出的失配损耗 )
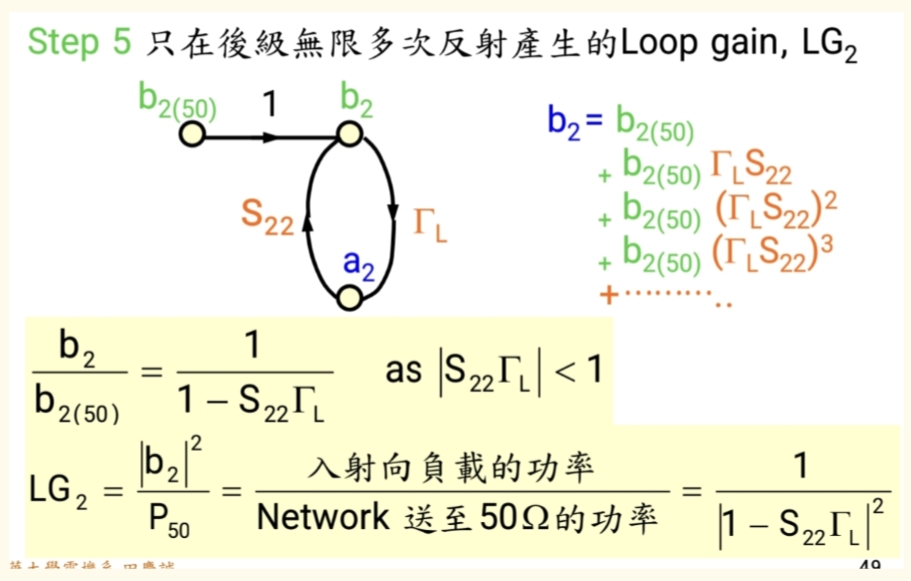
输出环路干涉Loop Gain_2
- 放大后的信号在输出端和负载之间经历多次反射和干涉。
- 数学因子 : ( 1∣1−S22ΓL∣2\frac{1}{|1 - S_{22}\Gamma_L|^2}∣1−S22ΓL∣21) (这是输出端M因子中的干涉效应项)
负载失配损耗MLM_LML
- 最终，从输出环路稳定下来的信号，要送入负载(ZLZ_LZL)。同样因为阻抗不匹配，最后一部分能量在这里被反射掉，无法被负载利用。
- 数学因子 : (1−∣ΓL∣21 - |\Gamma_L|^21−∣ΓL∣2) (这是输出端M因子中的负载失配项)
  
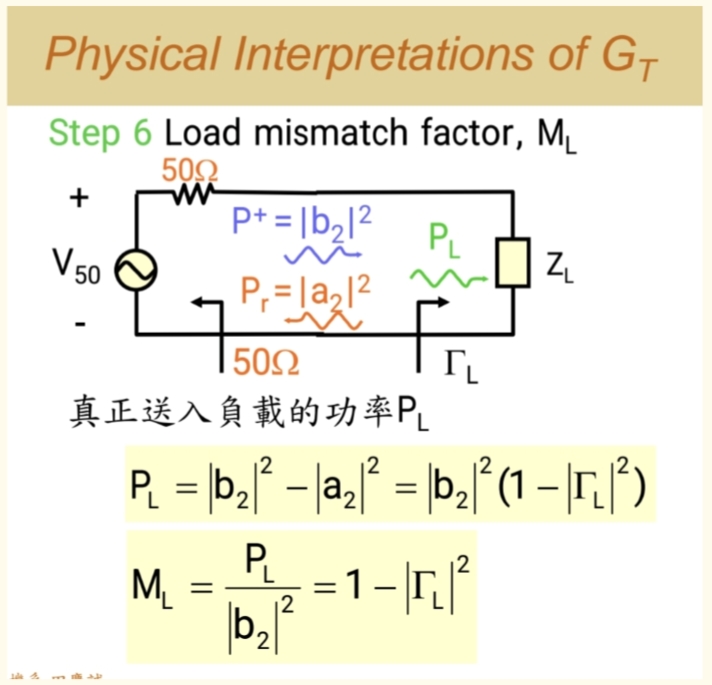
  总增益(GTG_TGT)就是这五项的乘积！ 设计高增益放大器，就是要最大化每一步的功率传输。可以看到，(GTG_TGT)的核心就是由多个"不匹配因子M"的物理过程构成的。

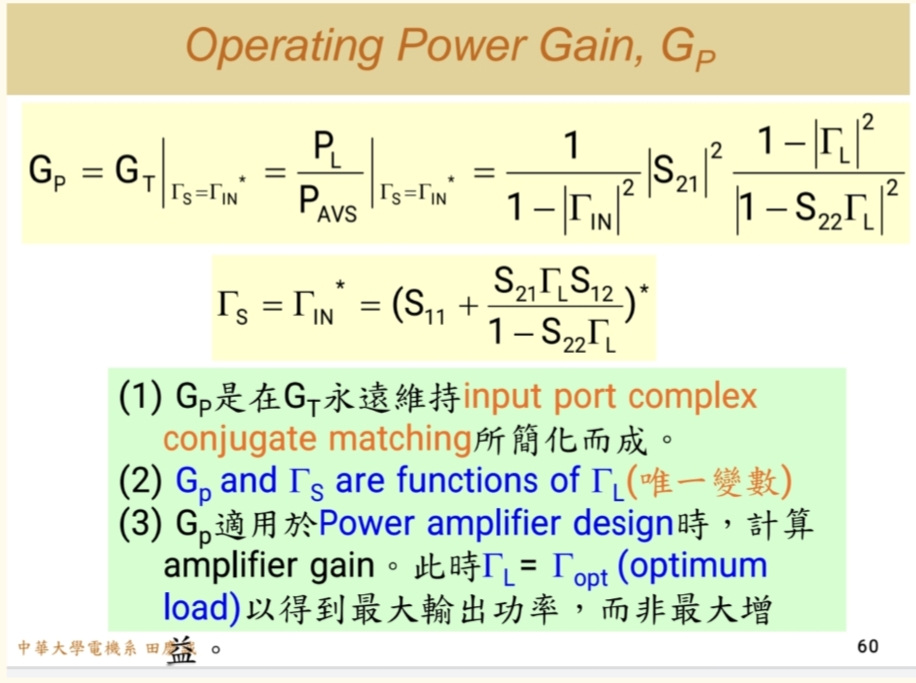
操作功率增益 (Operating Power Gain, (GPG_PGP))
- 定义 : (GP=PLPinG_P = \frac{P_L}{P_{in}}GP=PinPL)
  - (PinP_{in}Pin)：实际送入放大器输入端的功率。
- 适用场景 ：GPG_PGP描述的是，在给定负载端匹配(ΓLΓ_LΓL) 的情况下，放大器对实际输入功率的放大能力。它的核心在于输入端总是自动假设为共轭匹配(ΓS=ΓinΓ_S = Γ_{in}ΓS=Γin*)。
为何用于功率放大器？ 在PA设计中，我们最关心的是输出到负载的绝对功率(PLP_LPL) ，而不是增益。最大输出功率通常发生在负载阻抗为某个特定ΓoptΓ_{opt}Γopt（最佳功率匹配点）时，这通常不是共轭匹配点。此时，ΓLΓ_LΓL被固定了（由功率输出能力决定），我们通过设计输入匹配网络来确保尽可能多的功率进入放大器（即输入端共轭匹配）。G_P的定义完美契合了这一场景：ΓLΓ_LΓL固定（由功率决定），输入端共轭匹配（最大化输入功率） 。因此，GPG_PGP是衡量PA性能的常用指标 。
可用功率增益 (Available Power Gain, (GAG_AGA))
- 定义 : (GA=PavnPavsG_A = \frac{P_{avn}}{P_{avs}}GA=PavsPavn)
  - (PavnP_{avn}Pavn)：放大器 能够提供的最大可用输出功率（当负载与放大器输出共轭匹配时）。
- 适用场景 ：GAG_AGA描述的是，在给定源端匹配(ΓSΓ_SΓS) 的情况下，放大器自身能向外提供的最大功率能力。它的核心在于输出端总是自动假设为共轭匹配(ΓL=ΓoutΓ_L = Γ_{out}ΓL=Γout*)。
- 为何用于低噪声放大器？
  在设计LNA时，我们的首要目标是最小化噪声系数，而不是最大化增益。晶体管的噪声系数主要取决于源阻抗(ΓSΓ_SΓS)。为了达到最低噪声，我们必须将ΓSΓ_SΓS设置为一个特定的值ΓoptΓ_{opt}Γopt（最佳噪声匹配点），这通常不是最大增益所需的共轭匹配点。
  此时，ΓSΓ_SΓS被固定了，我们唯一能优化的就是输出匹配网络。而GAG_AGA的定义正好契合了这一场景：ΓSΓ_SΓS固定（由噪声决定），输出端共轭匹配（最大化输出功率） 。因此，GAG_AGA是衡量LNA性能的天然指标 。
  当用于设计lna的时候，GAG_AGA又被称为associated gain

【第四部分小结与衔接】

我们明白了增益有多种定义，而(GTG_TGT)是核心，它描述了功率传输的完整链条，而这个链条的本质是一系列M因子的串联 ，这也能够通过我们整个推导过程中能体现出来。而出于不同的设计目的，我们学习新的功率增益来利用，比如设计lna，我们前级匹配电路 并非寻找共轭入射系数，而是寻找最小化噪声的反射系数，于此同时，后级匹配电路 则是设计为完美匹配，于是我们学习新的功率增益GAG_AGA。

第五部分：理想与现实

在实际工程中，一个常见且令人困惑的问题是：为什么我用软件仿真计算出的转换功率增益（GTG_TGT），和用网络分析仪实际测量到的结果，总是对不上？

这个问题的根源在于：理论仿真模型与现实物理电路之间存在一个关键的"理想化 gap"------即匹配网络的损耗。

5.1 理论仿真（软件计算）的"理想世界"

当你在仿真软件（如ADS、Cadence）中计算GTG_TGT时，过程是这样的：

输入：晶体管的S参数，以及你设定的源反射系数（ΓSΓ_SΓS）和负载反射系数（ΓLΓ_LΓL）。
输出：软件根据GTG_TGT的经典公式，直接算出一个增益值。

关键局限 ：软件默认你提供的 ΓSΓ_SΓS 和 $Γ_L$ 是直接、无损耗地 加在晶体管端口上的。它完全没有考虑 你是通过一个由实际元件（电感、电容、传输线）构成的、必然存在损耗 的匹配网络来实现这些 ΓSΓ_SΓS和 ΓLΓ_LΓL 的。

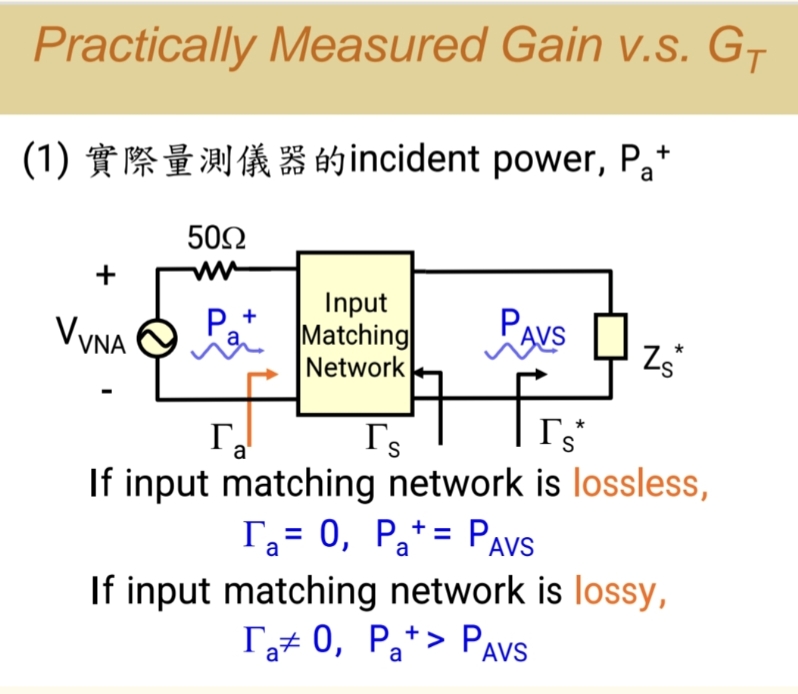
5.2 实际测量（网络分析仪）的"现实世界"

当你制作出实际的放大器电路并用网络分析仪测量时：

网络分析仪的输出端口提供一个50Ω的源，它送出一个入射功率（a₁）。
这个信号必须先经过你设计的输入匹配网络，才能到达晶体管。
同样，晶体管放大后的信号，也必须先经过输出匹配网络，才能被网络分析仪的输入端口接收。

5.3 损耗如何导致误差：核心机制

现在，我们来看有损匹配网络如何系统地导致实测增益低于仿真增益。

在输入端：
- 仿真假设 ：源的最大可用功率（PAVSP_{AVS}PAVS）无损地送达晶体管输入端。
- 现实情况 ：输入匹配网络存在损耗（电阻、介质损耗等）。网络分析仪送出的功率，一部分被匹配网络自身消耗，另一部分甚至被反射。因此，真正到达晶体管输入端的 PAVSP_{AVS}PAVS(实际) 要小于仿真中使用的 PAVSP_{AVS}PAVS(理想)。
- 对增益的影响 ：GTG_TGT = PLP_LPL / PAVSP_{AVS}PAVS。分母（实际值） < 分母（理想值） 。
在输出端：
- 仿真假设 ：晶体管送出的功率（PAVNP_{AVN}PAVN）无损地送达负载。
- 现实情况 ：输出匹配网络也会消耗一部分功率。因此，最终到达网络分析仪的 PLP_LPL(实际) 要小于仿真计算的 PLP_LPL(理想)。
- 对增益的影响 ：分子（实际值） < 分子（理想值） 。

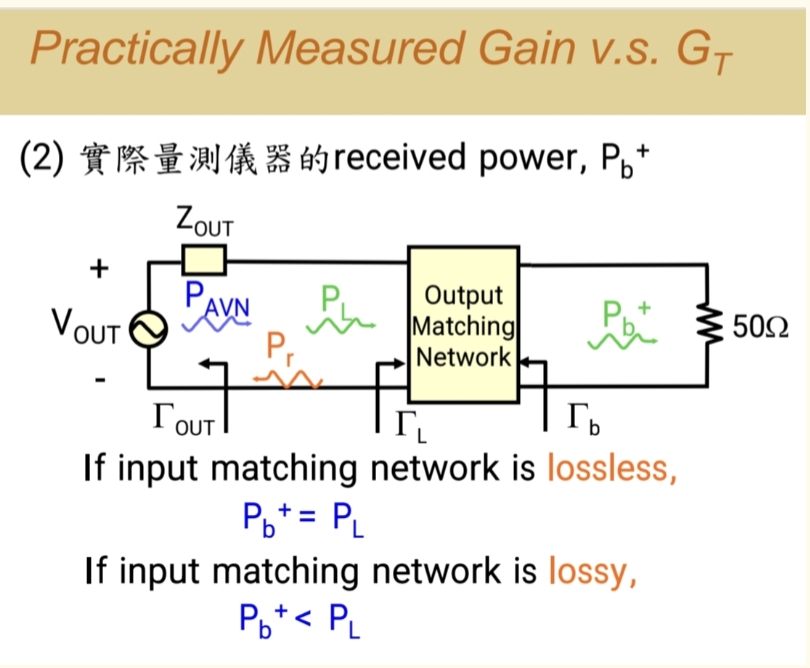
综合效应 ：一个有损的系统，使得增益公式中的分子和分母同时变小 。在绝大多数情况下，这个净效应会使得 GTG_TGT(实测) < GTG_TGT(仿真) 。你仿真时觉得性能很好，一做出来实测就"掉增益"，根本原因就在于此。

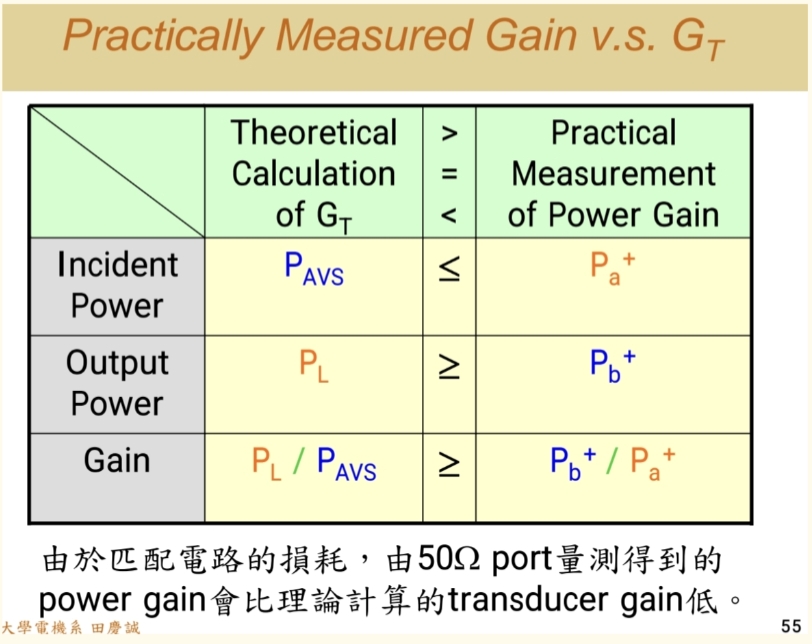
5.4 给工程师的关键工作流程与建议

因此，一个可靠的设计流程绝不能止步于理论计算：

第一步：理论计算与初步设计
- 使用晶体管的S参数，基于GTG_TGT公式进行初步计算和优化，找到最优的 ΓSΓ_SΓS 和 ΓLΓ_LΓL。这是一个重要的起点。
第二步:包含真实模型的协同仿真
- 将带有实际损耗模型的匹配电路（包括电感Q值、电容损耗、传输线损耗等）与晶体管模型一起，在仿真软件中构建完整的放大器电路。
- 然后，在这个完整电路的输入和输出端接上50Ω端口，进行S参数仿真。这时仿真得到的S₂₁，才是网络分析仪真正会测量到的结果。
- 只有这个仿真结果，才能准确预测实测性能。

结论：

不要认为软件计算GTG_TGT的结果就是最终电路的性能。那个结果是理想上限 。你必须通过包含所有寄生效应和损耗的系统级仿真 来桥接理想与现实。记住这句忠告："你还要把匹配电路放进去再仿真一次S₂₁，这个才是网络分析仪最终看到的（结果）。" 这样才能避免"仿真一时爽，实测火葬场"的尴尬局面。

第六部分：最大增益的实现

前面我们学习了GTG_TGT,并在第三部分知道了当反射系数达到共轭匹配的时候，不匹配因子M=1,此时能够输出最大功率增益，那这个最大功率增益为多少呢？这就是我们本节要研究的内容。

6.1 最大转换功率增益与同时共轭匹配

目标：找到一组唯一的 ΓSΓ_SΓS和ΓLΓ_LΓL，使得GTG_TGT达到其理论最大值，记为GTmaxG_{Tmax}GTmax或MAG。
条件：实现GTmaxG_{Tmax}GTmax的条件是同时共轭匹配：
- 输入端 ： ΓS=ΓinΓ_S = Γ_{in}ΓS=Γin*
- 输出端 ： ΓL=ΓoutΓ_L = Γ_{out}ΓL=Γout*
挑战与求解 ：由于双向性效应（ΓinΓ_{in}Γin是ΓLΓ_LΓL的函数，ΓoutΓ_{out}Γout是ΓSΓ_SΓS的函数），这两个方程是耦合的。通过联立求解，可以得到一组唯一的解ΓMSΓ_{MS}ΓMS和ΓMLΓ_{ML}ΓML。现代EDA软件（如ADS）可以一键计算出这些值。在求解出对应的唯一解ΓMSΓ_{MS}ΓMS和ΓMLΓ_{ML}ΓML后，再从50欧姆往后退设计出对应的匹配网络。
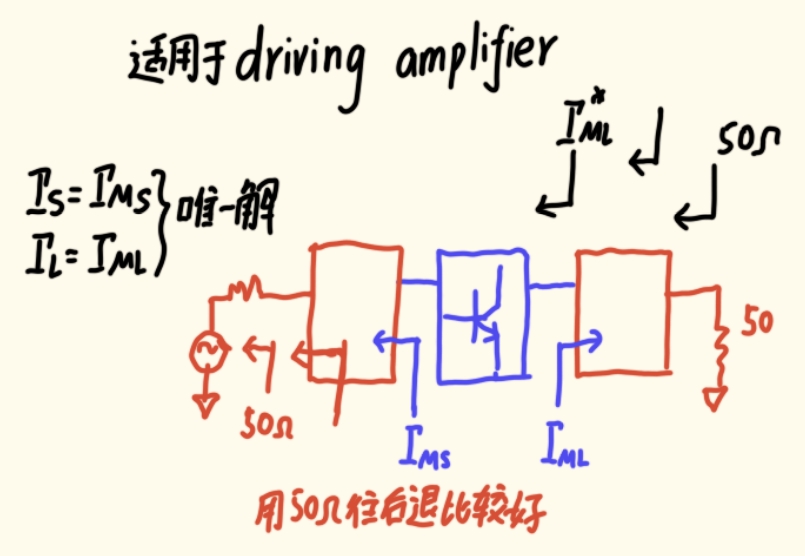
前提条件 ：只有当晶体管是 unconditional stable (K>1) 时，这组解才存在且物理可实现。

6.2 最大稳定增益MSG

问题：如果晶体管是潜在不稳定的(K<1)，则不存在实现同时共轭匹配的物理解，因而MAG也不存在。
解决方案 ：此时，我们通过在外围添加电阻等损耗元件，来"吃掉"多余的增益，强制使电路变得稳定(K≥1)。这个过程称为稳定化。
最大稳定增益 ：定义为当K=1时所能达到的增益。其计算公式为： $MSG=∣S21∣∣S12∣MSG = \\frac{\|S_{21}\|}{\|S_{12}\|}MSG=∣S12∣∣S21∣$ (由定义我们也可以看出，MSG始终要比MAG要大)
物理意义 ：MSG是一个晶体管在稳定前提下所能提供增益的理论上限。任何稳定化设计后的实际增益都不会超过MSG。
工程应用 ：MSG是一个极其有用的快速评估工具 。拿到一个晶体管的数据手册，你可以立即用(∣S21∣)(|S_{21}|)(∣S21∣)和(∣S12∣)(|S_{12}|)(∣S12∣)的dB值估算出MSG≈(∣S21∣dB−∣S12∣dB)MSG ≈ (|S_{21}|{dB} - |S{12}|_{dB})MSG≈(∣S21∣dB−∣S12∣dB) / 2。这让你在深入设计前就能判断该晶体管能否满足你的增益需求。

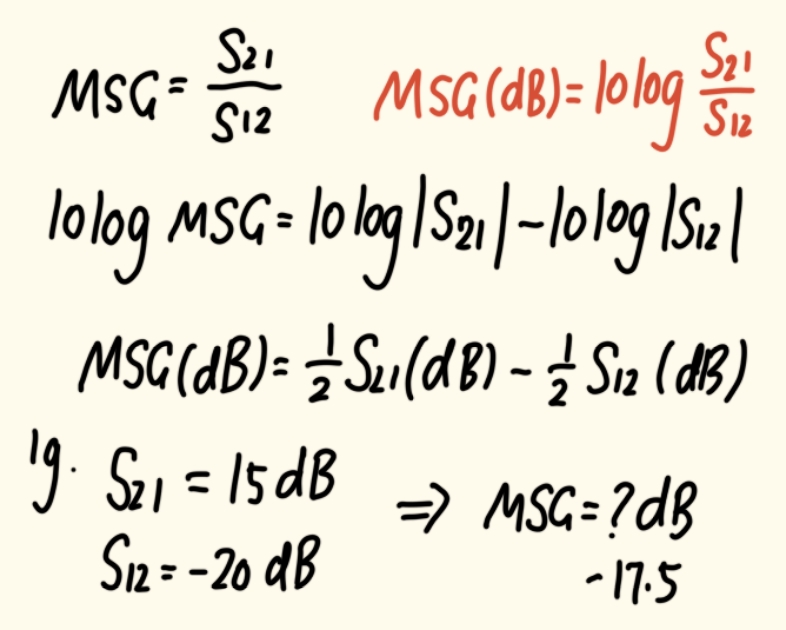
6.3 单向性设计GTUG_{TU}GTU

理想假设 ：如果晶体管是单向的 ，即S₁₂ = 0（反向传输为零），那么双向性效应消失。此时，Γin=S11，Γout=S22Γ_{in} = S₁₁，Γ_{out} = S₂₂Γin=S11，Γout=S22。
带来的简化 ：
1. 输入输出解耦 ：输入和输出匹配可以完全独立地进行设计(但尽量少用，大多数元件都不是单向元件)。
2. 增益计算简化 ：总增益G_TU等于三项的乘积： $GTU=1−∣ΓS∣2∣1−S11ΓS∣2×∣S21∣2×1−∣ΓL∣2∣1−S22ΓL∣2\]\[ G_{TU} = \\frac{1 - \|\\Gamma_S\|\^2}{\|1 - S_{11}\\Gamma_S\|\^2} \\times \|S_{21}\|\^2 \\times \\frac{1 - \|\\Gamma_L\|\^2}{\|1 - S_{22}\\Gamma_L\|\^2}\]\[GTU=∣1−S11ΓS∣21−∣ΓS∣2×∣S21∣2×∣1−S22ΓL∣21−∣ΓL∣2$ 第一项是输入匹配网络的增益，第三项是输出匹配网络的增益，中间是晶体管的本征增益。
3. 最大增益 ：当ΓS=S11Γ_S = S₁₁ΓS=S11*且ΓL=S22Γ_L = S₂₂ΓL=S22*时，GTUG_{TU}GTU达到最大。
现实与误差 ：没有晶体管是完美单向的。但若S₁₂足够小，可以近似为单向。引入单向化优值因数 可以估算由此带来的增益误差。当误差很小时，采用单向化设计可以大大简化过程。
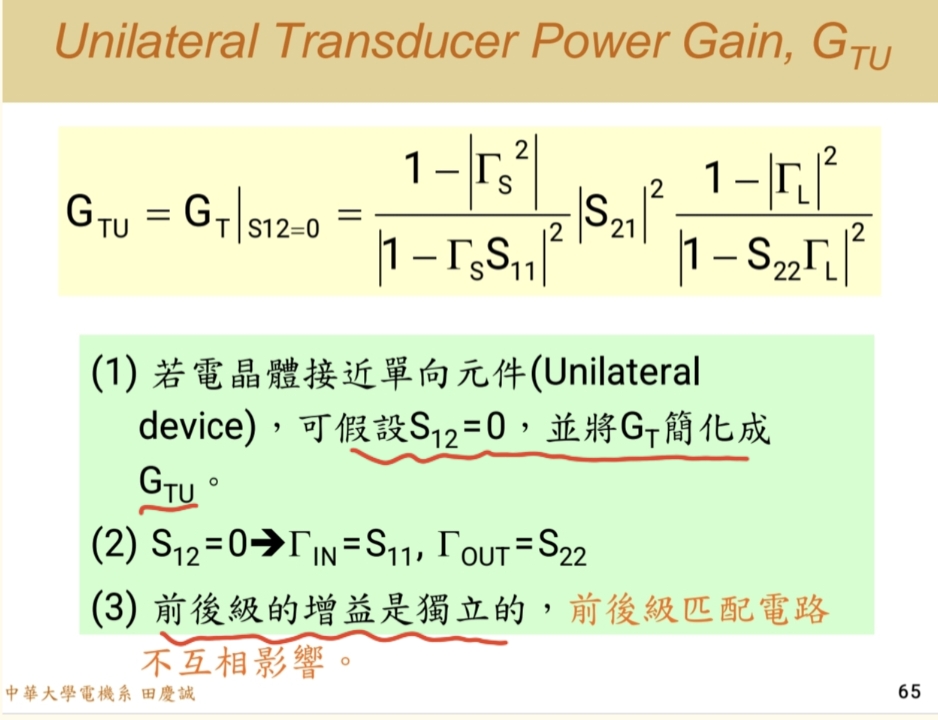
最大增益 ：类似的，当前后级共轭匹配时，有最大的增益输出GTU,MAXG_{TU,MAX}GTU,MAX

第七部分：频率极限与工程实践

剩下就是补充一些关于频率的定义。

7.1 关键频率指标的定义

fₛ - 单位电流增益频率
- 定义：当晶体管的电流增益 下降到 1 (0 dB) 时的频率。
- 重要性：这个参数现在较少使用，知道这个概念即可。
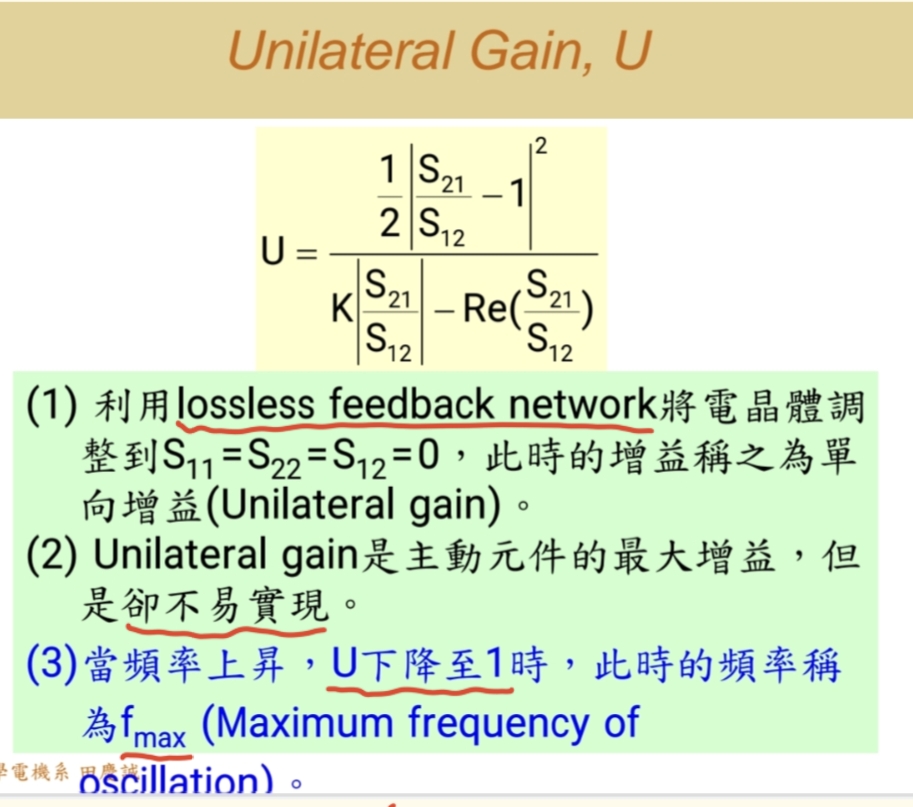
U - 单向化增益
- 目标：通过复杂的外部电路（如无损反馈、输入输出匹配），人为地将一个非单向性晶体管（S12≠0S₁₂ ≠ 0S12=0）改造为"理想单向"器件。改造目标是使其 S11=0,S22=0,S12=0S₁₁ = 0, S₂₂ = 0, S₁₂ = 0S11=0,S22=0,S12=0 ，只剩下 S21S₂₁S21。
- 定义：在上述理想条件下能够实现的最大增益，即为单向化增益 U。
- 现实意义 ：这个目标在现实中极难实现 ，尤其需要"无损反馈"电路，因此 U 主要是一个理论上的极限值。
fₘₐₓ - 最大振荡频率
- 定义：晶体管的单向化增益 U 下降到 1 (0 dB) 时的频率。
- 物理意义 ：这是晶体管能够产生振荡的绝对上限频率 。超过 fₘₐₓ，即使使用最理想的反馈和匹配电路，也无法让电路产生振荡或提供任何增益。

7.2 工程实践中的简化：从 U 到 MSG/MAG

由于单向化增益 U 不切实际，所以我们常用的还是上一部分提到的MSG 和MAG。

MSG - 最大稳定增益
- 当晶体管潜在不稳定（稳定因子 K = 1）时，它能提供的最大增益称为 MSG。
MAG - 最大可用增益
- 当晶体管绝对稳定（稳定因子 K > 1）时，通过共轭匹配能在输入输出端同时获得的最大增益称为 MAG。

核心关系 ：MSG/MAG 的曲线是工程师真正依赖的设计工具。U 的理论曲线和 MSG/MAG 的实测曲线在形状和数值上通常非常接近。因此，在实践中，我们直接观察 MSG/MAG 曲线 ，并定义：
fmaxfₘₐₓfmax(工程定义) ≈ MAGMAGMAG下降到 1 (0 dB) 时所对应的频率。

7.3 如何从图表中快速估算 fmaxfₘₐₓfmax

当网络分析仪的频率范围无法直接测量到 fₘₐₓ 时（例如仪器上限13.5 GHz，但 fₘₐₓ 在24 GHz），我们可以通过图表外推：

识别曲线拐点：在 MSG/MAG 曲线上，找到其开始以稳定斜率下降的区段（通常对应 K 因子开始趋近或大于1的区域）。
确定下降斜率 ：在该区段，增益通常以 每倍频 6 dB 或 每十倍频 20 dB 的规律下降。
图形外推：沿着这个确定的斜率向下画延长线，直到与 0 dB 增益线相交，交点对应的频率即为估算的 fₘₐₓ。

举例：如图表所示，在频率超过约6 GHz后，蓝色 MAG 曲线开始以固定斜率下降（在K≤1时，MAG根本不存在，因此软件直接将MAG和MSG曲线重合绘制）。将此直线延长至与0 dB线相交，即可估算出 fₘₐₓ 约为 24 GHz。

问题：已知某晶体管的 fₘₐₓ 为 24 GHz，请问要设计一个增益为 10 dB 的放大器，其最高工作频率大约是多少？

解答：

增益从 0 dB (在 fₘₐₓ 处) 增加到 10 dB，需要提升 10 dB。根据 -6 dB/倍频程的规律，频率需要向回找。10 dB 大约是 6 dB 的 1.67倍。因此，频率比例关系为 ( 2(10/6)≈21.67≈3.22^{(10/6)} \approx 2^{1.67} \approx 3.22(10/6)≈21.67≈3.2)。所以，最高工作频率 ≈ fₘₐₓ / 3.2。
计算结果 ：24 GHz / 3.2 ≈ 7.5 GHz。