🟢 写在前面:为什么你必须懂加法器?
各位老铁好,我是你们的底层技术搭子。
很多写业务代码的同学可能会觉得:"我就是一个调包侠,int a = b + c 这一行代码,CPU 到底怎么跑的关我什么事?"
如果你只想做个 CRUD 工程师,那确实没关系。但如果你想成为架构师,想理解并发原本 ,想知道为什么整数溢出会导致安全漏洞,甚至想理解为什么 CPU 的主频卡在 5GHz 很难再上去了,那你必须得懂加法器。
加法器(Adder)是 CPU 中 ALU(算术逻辑单元) 的心脏。你以为 CPU 真的很智能吗?其实它最擅长的事情只有一个:做加法。减法是加法(补码),乘法是累加,除法是累减。搞懂了加法器,你就搞懂了计算机运算能力的基石。

一、 拆解需求:我们在设计什么?
在开始画电路图之前,我们先回到小学数学课堂。
假设我们要计算 7+12=197 + 12 = 197+12=19。
在计算机内部,这其实是两个 8-bit(或 n-bit)二进制数的运算:
000001112+000011002=00010011200000111_2 + 00001100_2 = 00010011_2000001112+000011002=000100112
1.1 加法器的基本黑盒模型
从宏观上看,1 无论是 8086 还是最新的 i9 处理器,加法器的输入输出接口模型是固定的:
-
输入(Input):
-
被加数 AAA(n bit)
-
加数 BBB(n bit)
-
低位进位 CinC_{in}Cin(1 bit,通常最低位为0,但在级联时很重要)
-
-
输出(Output):
-
和 SSS(n bit,运算结果)
-
进位输出 CoutC_{out}Cout(1 bit,表示结果是否超出了 n bit 的表示范围)
-
我们的目标,就是设计一个由逻辑门(AND, OR, NOT, XOR)组成的电路,填满这个黑盒子。
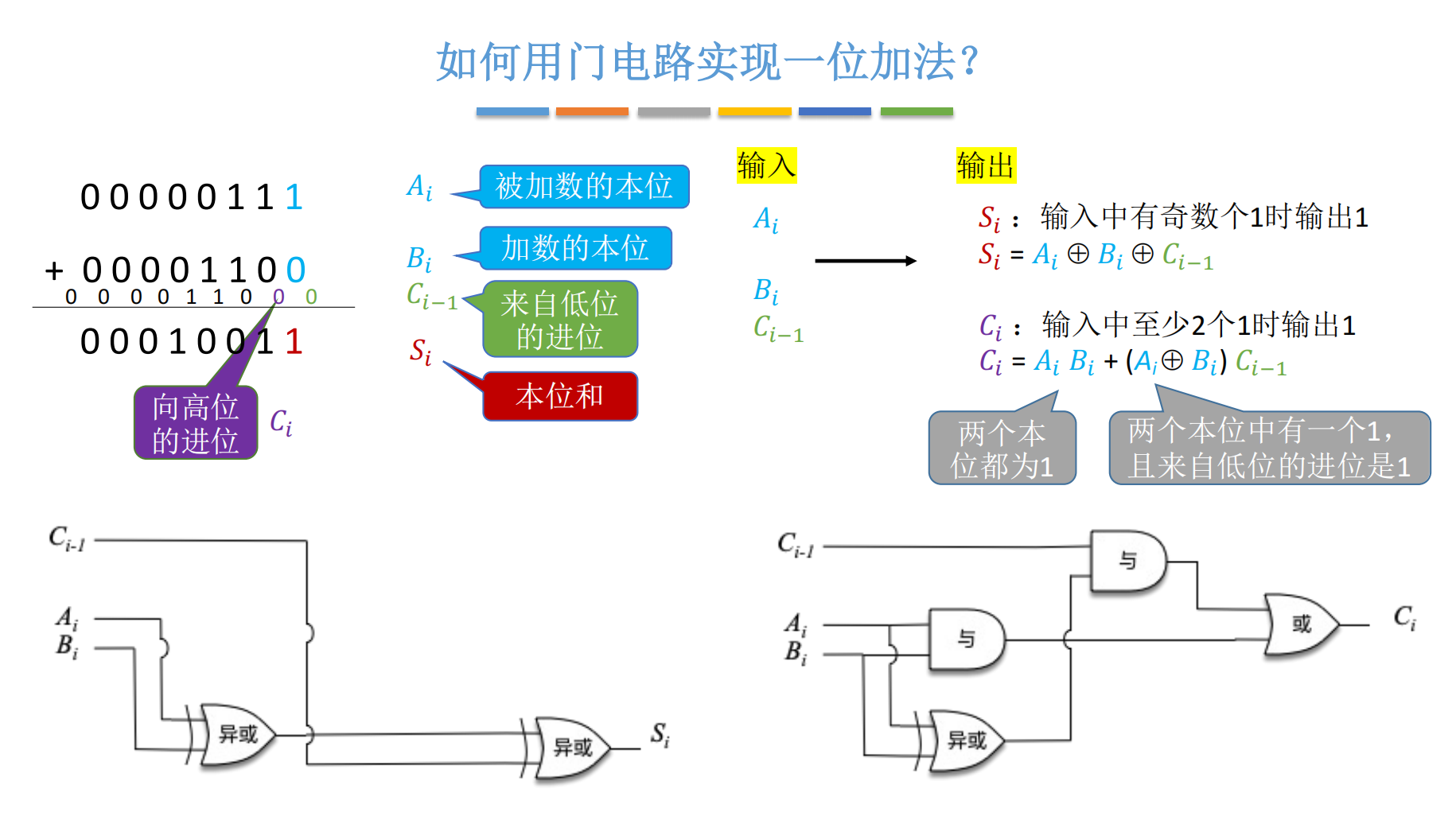
二、 从零开始:一位全加器(FA)的设计
罗马不是一天建成的,n 位加法器也是由 1 位加法器拼出来的。我们先把目光聚焦到某一个比特位的运算上。
2.1 什么是"全"加器?
为什么叫"全加器"(Full Adder, FA)?
-
半加器(Half Adder): 只管两个本位 AiA_iAi 和 BiB_iBi 相加,不考虑低位进位。这显然是不够的,除了最低位,其他位都要处理进位。
-
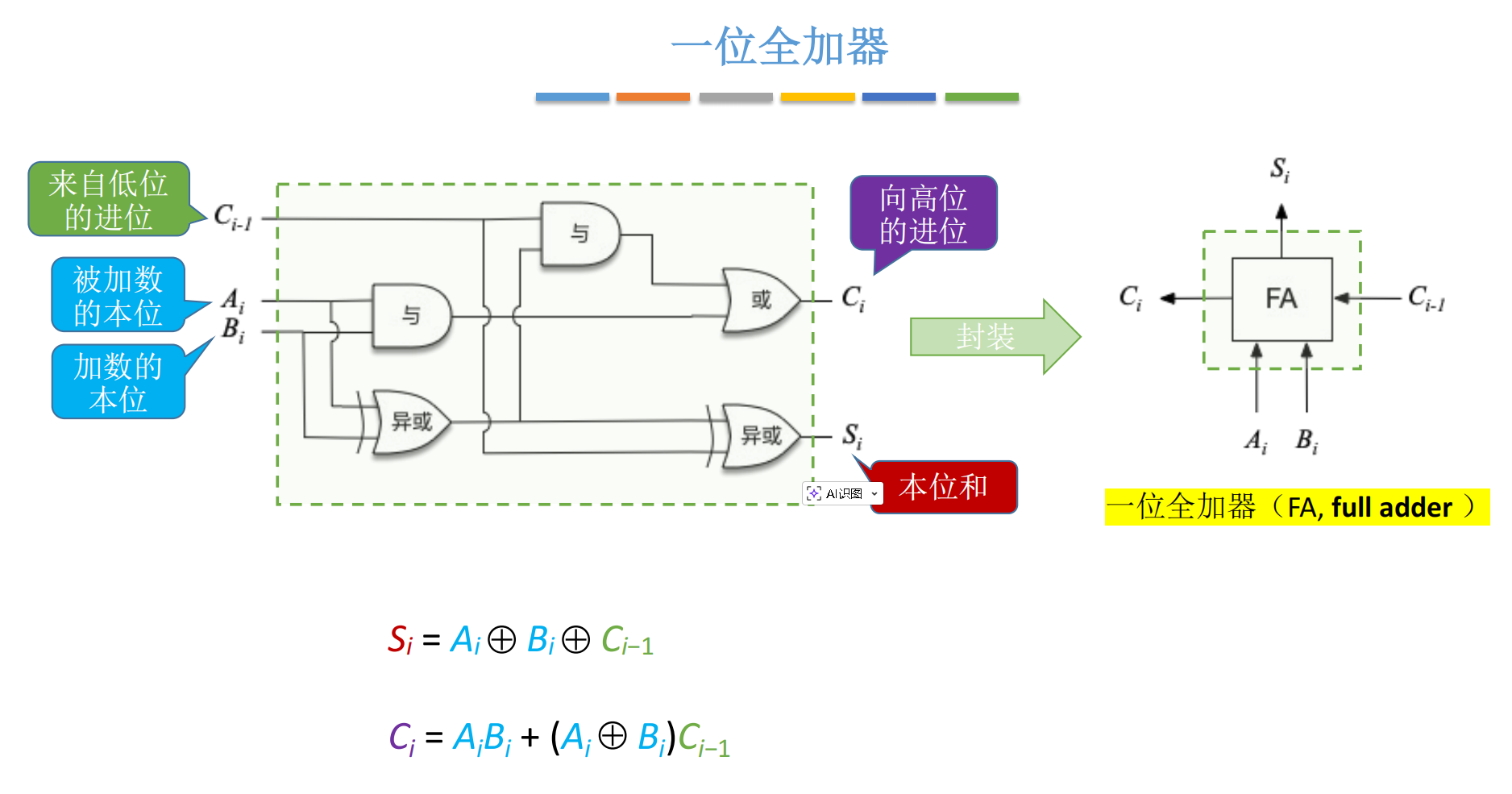
全加器(Full Adder): 考虑了三个输入------本位被加数 AiA_iAi、本位加数 BiB_iBi、来自低位的进位 Ci−1C_{i-1}Ci−1。 2
2.2 逻辑推导:像机器一样思考
对于第 iii 位的运算,我们需要输出两个值:本位和 SiS_iSi 和向高位的进位 CiC_iCi。
(1) 本位和 SiS_iSi 的逻辑
想象一下二进制相加:
-
如果 Ai,Bi,Ci−1A_i, B_i, C_{i-1}Ai,Bi,Ci−1 中有 0个 或 2个 是 1,和为 0。
-
如果 Ai,Bi,Ci−1A_i, B_i, C_{i-1}Ai,Bi,Ci−1 中有 1个 或 3个 是 1,和为 1。
这本质上是一个"奇偶校验"逻辑!
只要输入中 1 的个数是奇数,输出就是 1。在数字逻辑中,完美的对应运算就是 异或(XOR, ⊕\oplus⊕)。
因此,本位和的逻辑表达式为:3
Si=Ai⊕Bi⊕Ci−1S_i = A_i \oplus B_i \oplus C_{i-1}Si=Ai⊕Bi⊕Ci−1
(2) 进位输出 CiC_iCi 的逻辑
什么时候我们需要向高位进位(即 Ci=1C_i = 1Ci=1)?
很简单,三个输入里,只要有 两个或两个以上 为 1,就得进位。这是一次"少数服从多数"的投票。
我们可以拆解为两种情况:
-
自带进位: AiA_iAi 和 BiB_iBi 都是 1。此时不管低位有没有进位,我都要进位。即 Ai⋅BiA_i \cdot B_iAi⋅Bi。
-
传递进位: AiA_iAi 和 BiB_iBi 中有一个是 1,且低位进位 Ci−1C_{i-1}Ci−1 也是 1。即 (Ai⊕Bi)⋅Ci−1(A_i \oplus B_i) \cdot C_{i-1}(Ai⊕Bi)⋅Ci−1。
合并起来,逻辑表达式为:4
Ci=AiBi+(Ai⊕Bi)Ci−1C_i = A_i B_i + (A_i \oplus B_i)C_{i-1}Ci=AiBi+(Ai⊕Bi)Ci−1
👨💻 博主注:
很多教科书会把第二项写成 (Ai+Bi)Ci−1(A_i + B_i)C_{i-1}(Ai+Bi)Ci−1。但在实际电路设计中,复用 SiS_iSi 计算中已经产生的 Ai⊕BiA_i \oplus B_iAi⊕Bi 信号可以节省逻辑门数量。这就是工程优化的细节。
我们将这个电路封装起来,就得到了一个标准的 FA(Full Adder) 模块。5
三、 暴力美学:串行进位加法器(RCA)
有了 FA 模块,要实现 n bit 加法器最简单的办法是什么?
套娃。
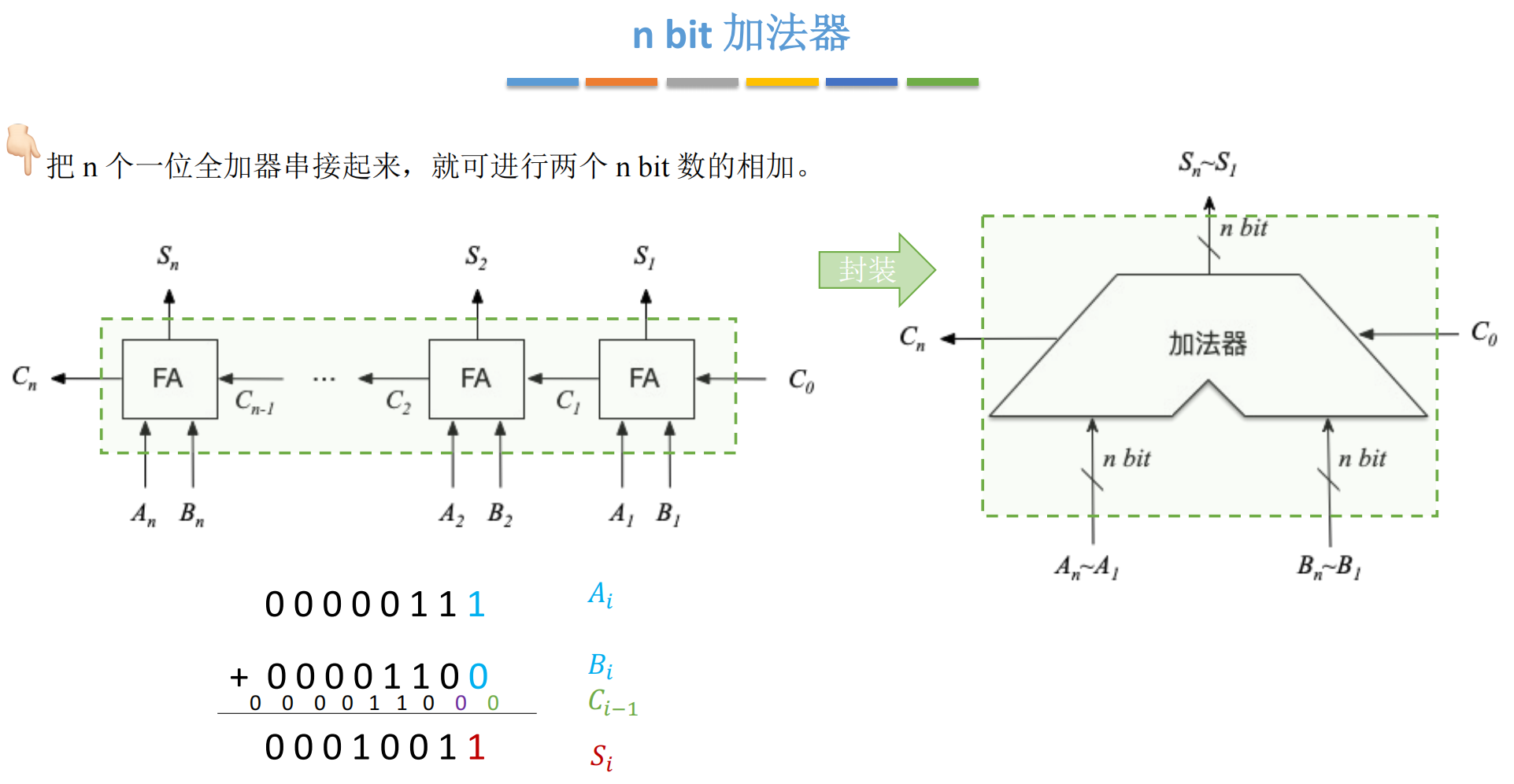
3.1 串联原理
像多米诺骨牌一样,我们将 n 个 FA 首尾相连:
-
第 0 位的 CoutC_{out}Cout 连到第 1 位的 CinC_{in}Cin。
-
第 1 位的 CoutC_{out}Cout 连到第 2 位的 CinC_{in}Cin。
-
...以此类推。
这种结构被称为 串行进位加法器(Ripple Carry Adder, RCA),又叫行波进位。6666
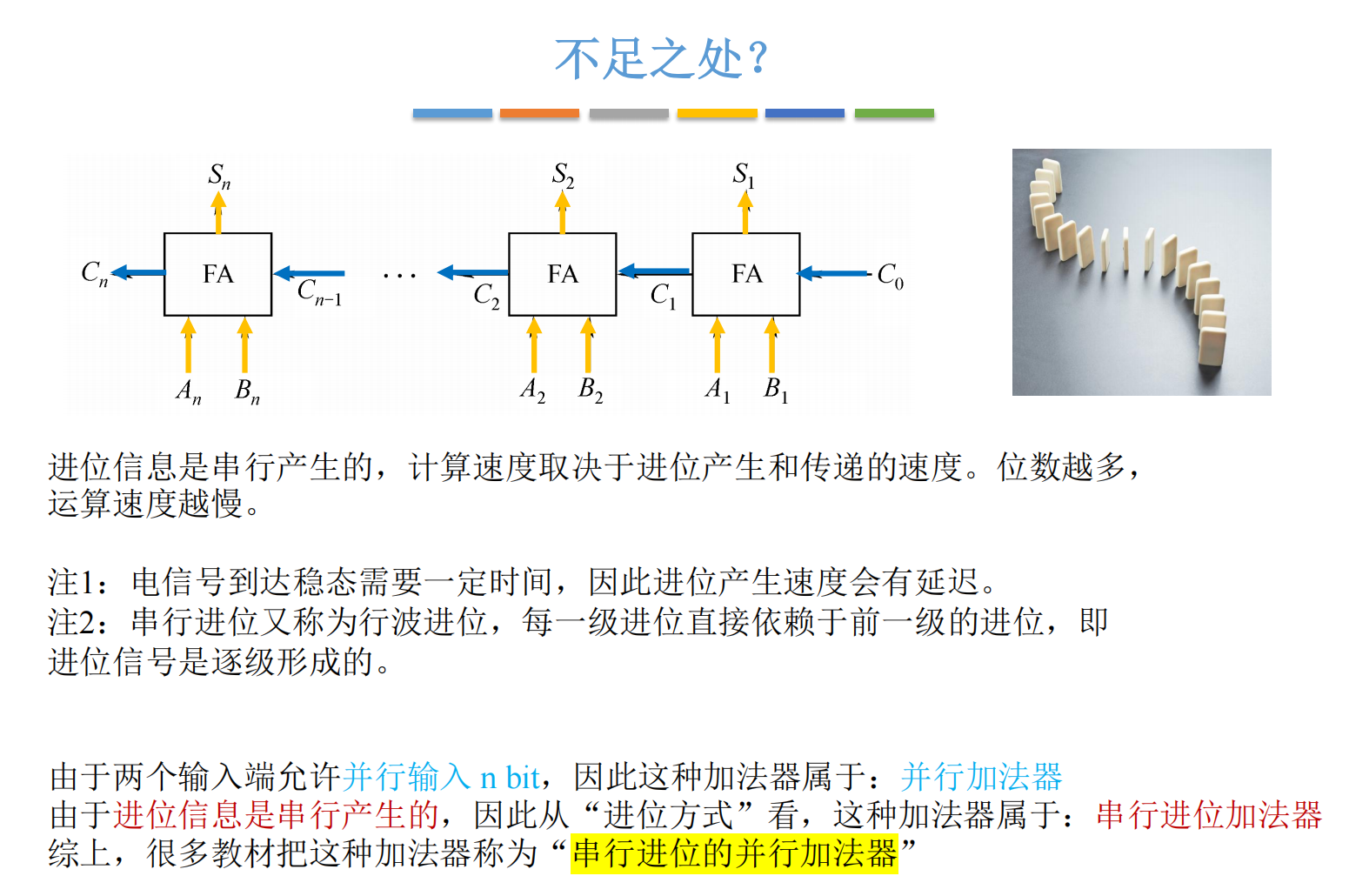
3.2 致命缺陷:速度的瓶颈
这个设计有一个致命的问题:延迟(Delay)。 777777777
请注意,第 iii 位的 FA 必须等待第 i−1i-1i−1 位计算出 Ci−1C_{i-1}Ci−1 之后,才能计算出它自己的 CiC_iCi。
这就好比排队报数,最后一个人必须等前面所有人都报完数,才能知道结果。
让我们算一笔账:
假设一个逻辑门的延迟是 TTT。生成一个进位信号大约需要 2级门延迟(2T2T2T)。
如果是 64 位的 CPU:
Total Delay≈64×2T=128T\text{Total Delay} \approx 64 \times 2T = 128TTotal Delay≈64×2T=128T
这就是为什么早期的 CPU 频率上不去的核心原因之一。 这种线性的延迟随着位数的增加而变得不可接受。
四、 速度的革命:并行进位加法器(CLA)
为了解决"等进位"的问题,天才的工程师们想:我们能不能在运算开始的瞬间,就直接预判出所有位的进位信息?
这就是 超前进位加法器(Carry Lookahead Adder, CLA),也就是笔记中提到的"并行进位的并行加法器"。
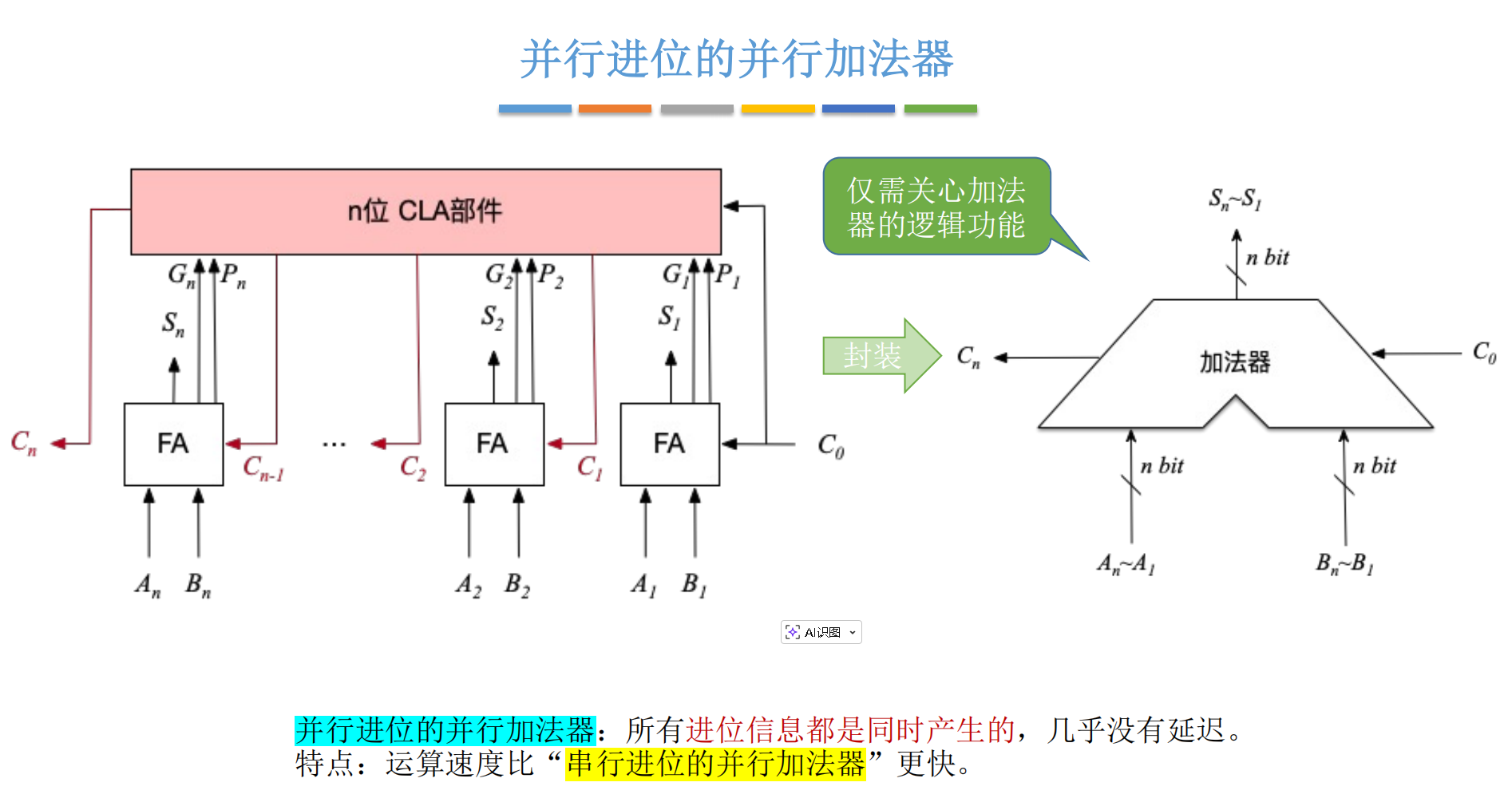
4.1 预判的艺术:G 和 P
我们要引入两个核心概念:
-
进位生成函数 (Generate, GiG_iGi):
Gi=Ai⋅BiG_i = A_i \cdot B_iGi=Ai⋅Bi含义:如果 AiA_iAi 和 BiB_iBi 都是 1,那么这一位一定会产生进位,不管低位是什么。
-
进位传递函数 (Propagate, PiP_iPi):
Pi=Ai⊕BiP_i = A_i \oplus B_iPi=Ai⊕Bi
含义:如果 AiA_iAi 和 BiB_iBi 中有一个是 1,那么它会将低位的进位原封不动地传递给高位。
4.2 展开递归(高能预警)
有了 GGG 和 PPP,我们可以重写进位公式:
Ci=Gi+Pi⋅Ci−1C_i = G_i + P_i \cdot C_{i-1}Ci=Gi+Pi⋅Ci−1
现在,我们来玩一个"套娃展开"的游戏(这是 CLA 的灵魂):
-
第 1 位进位 C1C_1C1:
C1=G0+P0C0C_1 = G_0 + P_0 C_0C1=G0+P0C0
-
第 2 位进位 C2C_2C2:
C2=G1+P1C1=G1+P1(G0+P0C0)=G1+P1G0+P1P0C0C_2 = G_1 + P_1 C_1 = G_1 + P_1(G_0 + P_0 C_0) = G_1 + P_1 G_0 + P_1 P_0 C_0C2=G1+P1C1=G1+P1(G0+P0C0)=G1+P1G0+P1P0C0
-
第 3 位进位 C3C_3C3:
C3=G2+P2C2=G2+P2G1+P2P1G0+P2P1P0C0C_3 = G_2 + P_2 C_2 = G_2 + P_2 G_1 + P_2 P_1 G_0 + P_2 P_1 P_0 C_0C3=G2+P2C2=G2+P2G1+P2P1G0+P2P1P0C0
-
第 4 位进位 C4C_4C4:
C4=G3+P3G2+P3P2G1+P3P2P1G0+P3P2P1P0C0C_4 = G_3 + P_3 G_2 + P_3 P_2 G_1 + P_3 P_2 P_1 G_0 + P_3 P_2 P_1 P_0 C_0C4=G3+P3G2+P3P2G1+P3P2P1G0+P3P2P1P0C0
看懂了吗?
C4C_4C4 的表达式里,只包含 G0...G3G_0...G_3G0...G3、P0...P3P_0...P_3P0...P3 和最初的 C0C_0C0。
这些参数在 T=0T=0T=0 时刻都是已知的!我们不需要等待 C1,C2,C3C_1, C_2, C_3C1,C2,C3 算出来,我们可以直接用一堆与门和或门,一次性算出 C4C_4C4!10
4.3 性能 vs 成本的博弈
这种设计通过增加 CLA 部件 (一大坨复杂的逻辑门电路),实现了所有进位信息的并行产生。11111111
-
优点: 延迟几乎是常数级,不再随位数线性增加,极大提升了运算速度。12
-
缺点: 电路变得非常复杂,晶体管数量暴增(芯片面积变大,发热变大)。
👨💻 架构师视角:
现实中的 CPU(如 x86)通常采用折中方案:在 4位 或 8位 内部使用 CLA 并行进位,而在这 4-bit 组之间采用串行或其他优化进位。这是空间换时间的经典案例。
五、 赋予灵魂:带标志位的加法器
到目前为止,我们的加法器只能算出一串 0 和 1。但对于程序员来说,我们更关心这些数字背后的逻辑意义:结果是不是 0?有没有溢出?是不是负数?
这就需要我们在加法器的输出端,外挂一些逻辑电路来生成 状态标志位(Status Flags) 。这些标志位将被存入 CPU 的 程序状态字寄存器(PSW) 中,用于控制 if-else 跳转。13131313
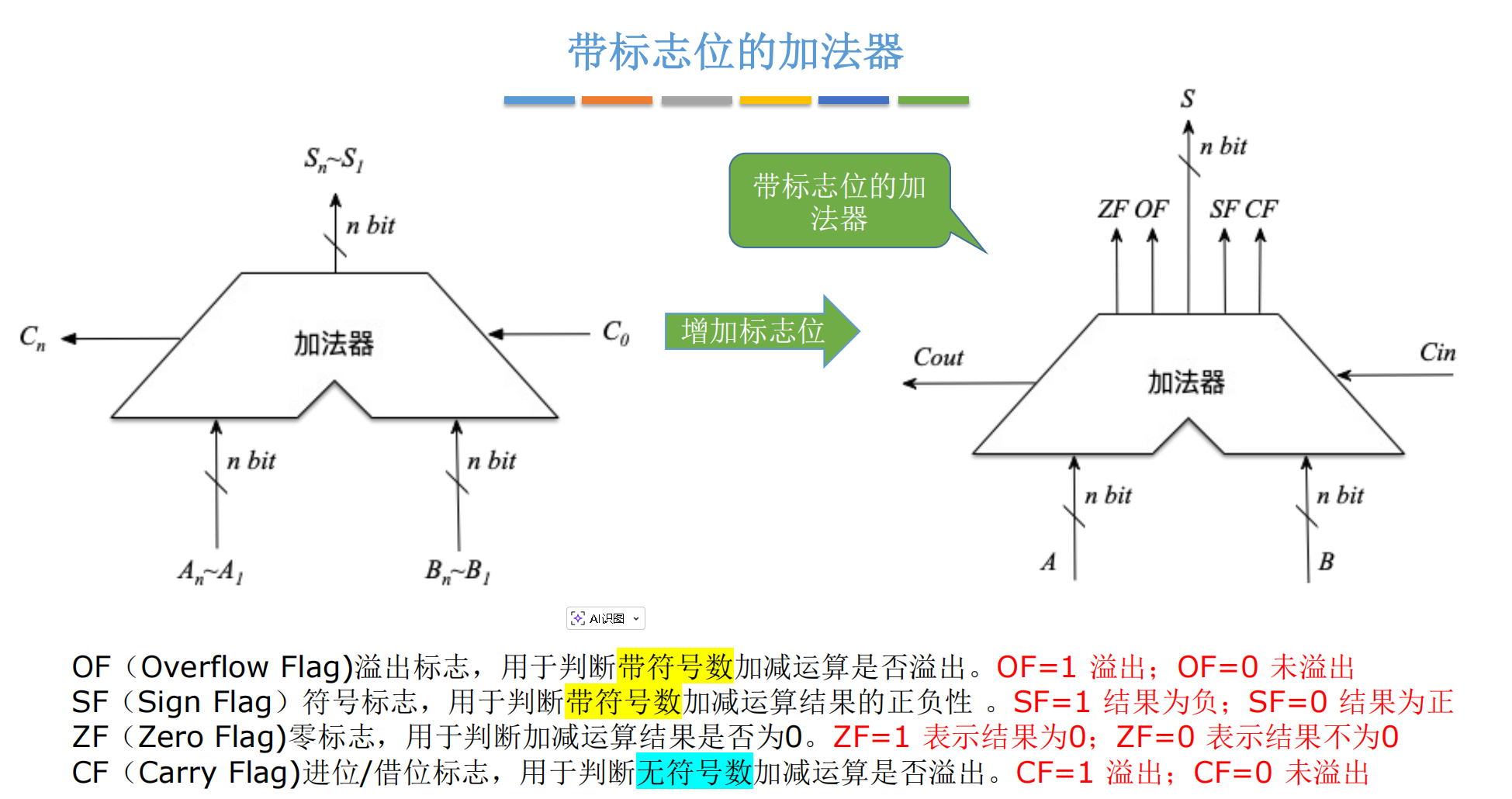
我们需要关注四个核心标志位:OF, SF, ZF, CF。
5.1 OF (Overflow Flag) - 溢出标志
-
作用: 专门用于 带符号数(Signed Integer) 的运算。判断结果是否超出了补码能表示的范围。14141414
-
原理: 只有"正+正"或"负+负"才可能溢出。
-
硬件逻辑:
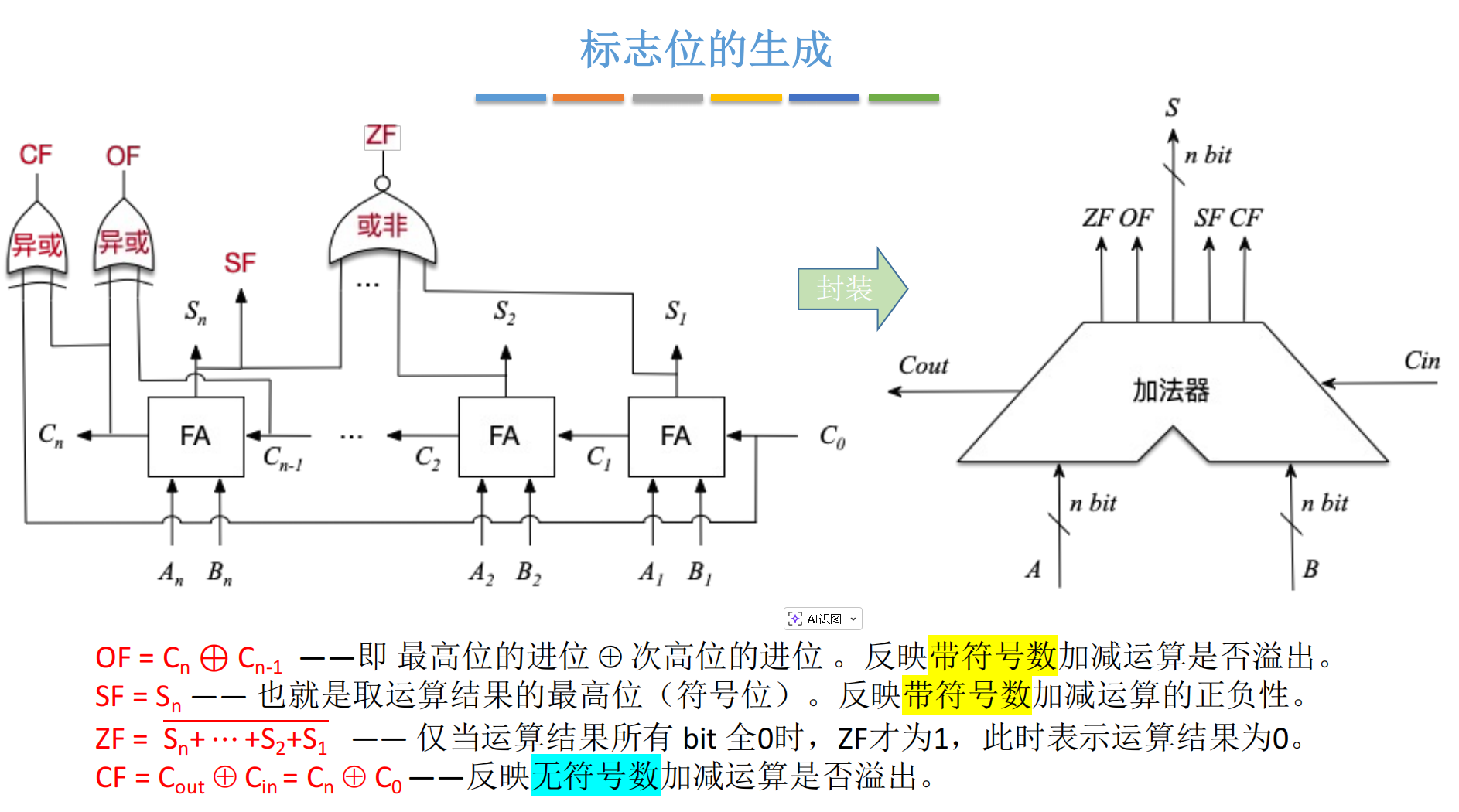
这也是考试常考点!判断逻辑非常巧妙:最高位的进位 CnC_nCn 异或 次高位的进位 Cn−1C_{n-1}Cn−1。15
OF=Cn⊕Cn−1OF = C_n \oplus C_{n-1}OF=Cn⊕Cn−1
-
OF=1OF=1OF=1:溢出(例如 127 + 1 = -128,崩了)。
-
OF=0OF=0OF=0:正常。
-
5.2 SF (Sign Flag) - 符号标志
-
作用: 判断结果是正数还是负数(仅对带符号数有意义)。16
-
硬件逻辑:
简单粗暴,直接取结果的最高位(Most Significant Bit, MSB)。17
SF=SnSF = S_nSF=Sn
-
SF=1SF=1SF=1:结果为负。
-
SF=0SF=0SF=0:结果为正(或0)。
-
5.3 ZF (Zero Flag) - 零标志
-
作用: 判断结果是否为 0。这是很多循环结束条件(如
i == 0)的判断依据。18 -
硬件逻辑:
如果要结果为 0,那么 S1S_1S1 到 SnS_nSn 必须全部为 0。我们可以用一个巨大的 或非门(NOR) 来实现。19
ZF=S1+S2+...+Sn‾ZF = \overline{S_1 + S_2 + ... + S_n}ZF=S1+S2+...+Sn
-
ZF=1ZF=1ZF=1:结果全为 0。
-
ZF=0ZF=0ZF=0:结果不为 0。
-
-
注意: ZF 标志位通吃有符号数和无符号数,通用性最强。20
5.4 CF (Carry Flag) - 进位标志
-
作用: 专门用于 无符号数(Unsigned Integer) 的运算。判断是否发生了进位或借位溢出。21212121
-
硬件逻辑:
根据提供的笔记资料,CF 的生成逻辑定义为:22
CF=Cout⊕CinCF = C_{out} \oplus C_{in}CF=Cout⊕Cin
即最高位进位输出与加法器初始进位输入的异或。
-
CF=1CF=1CF=1:无符号运算溢出。
-
CF=0CF=0CF=0:正常。
-
⚠️ 高手进阶(易混淆点):
很多同学搞不清 OF 和 CF 的区别。
如果你定义变量是
int(带符号),CPU 看 OF。如果你定义变量是
unsigned int(无符号),CPU 看 CF。CPU 其实不知道你存的是什么,它会同时算出 OF 和 CF,具体信哪个,取决于你的汇编指令(是
JG还是JA)!
六、 总结与展望
通过这一通操作,我们从最简单的异或门开始,一步步搭建出了一个支持 n 位并行计算、并行进位、且具备完善状态检测功能的现代加法器。
知识点浓缩表
| 概念 | 核心关键词 | 优缺点/特征 | 公式/逻辑 |
|---|---|---|---|
| 一位全加器 (FA) | 本位和, 进位 | 基础单元 | Si=Ai⊕Bi⊕Ci−1S_i = A_i \oplus B_i \oplus C_{i-1}Si=Ai⊕Bi⊕Ci−1 Ci=AiBi+(Ai⊕Bi)Ci−1C_i = A_i B_i + (A_i \oplus B_i)C_{i-1}Ci=AiBi+(Ai⊕Bi)Ci−1 |
| 串行进位 (RCA) | 行波进位, 延迟 | 结构简单,但慢 | 延迟 ∝n\propto n∝n (位数) |
| 并行进位 (CLA) | 提前预判, CLA部件 | 快,但电路复杂 | Gi,PiG_i, P_iGi,Pi 展开,同时产生进位 |
| OF (溢出) | 带符号数 | 最高位进位 ≠\neq= 次高位进位 | OF=Cn⊕Cn−1OF = C_n \oplus C_{n-1}OF=Cn⊕Cn−1 |
| CF (进位) | 无符号数 | 进位输出检测 | CF=Cout⊕CinCF = C_{out} \oplus C_{in}CF=Cout⊕Cin |
| ZF (零) | 全0检测 | 通用 | NOR(所有位) |
 |
🚀 博主想对你说
这就是计算机组成的魅力。看似简单的 1+1=21+1=21+1=2,底层却是无数逻辑门的精密协作。
下次当你按下键盘上的 Build 键,看着进度条飞快走动时,请记得:这背后是数十亿个微小的晶体管,正在以 CLA 的逻辑疯狂地进行着并行进位。
👉 下一步行动:
理解了加法器,减法器怎么设计?难道真的要重新设计电路吗?
剧透一下:不需要! 只需要利用补码特性,给加法器加几个非门就能变身减法器。
我们下篇文章再见!