Python数学：统计运算

文章目录

• [一、 描述统计](#一、 描述统计)
• • [1. 基本概念](#1. 基本概念)
  • [2. 使用方法](#2. 使用方法)
  • • [使用 NumPy 和 pandas 进行描述统计](#使用 NumPy 和 pandas 进行描述统计)
    • [使用 SciPy 计算偏度和峰度](#使用 SciPy 计算偏度和峰度)
  • [3. 应用场景](#3. 应用场景)
  • • 数据探索性分析（EDA）
    • 异常值检测
• [二、 概率运算](#二、 概率运算)
• • [1. 基本概念](#1. 基本概念)
  • [2. 使用方法](#2. 使用方法)
  • • [使用 SciPy 处理概率分布](#使用 SciPy 处理概率分布)
    • 二项分布和泊松分布
    • 贝叶斯定理应用
  • [3. 应用场景](#3. 应用场景)
  • • 蒙特卡洛模拟
    • 风险评估
• [三、 总结](#三、 总结)
• [四、 相关文章](#四、 相关文章)

---

统计运算是使用数学方法对数据进行收集、整理、分析和解释的过程。本篇介绍描述统计和概率运算。

一、 描述统计

描述统计是对数据进行整理、概括和可视化的过程，目的是用少量指标描述数据集的主要特征。

描述统计的核心是"用数说图"，将复杂数据简化为可理解的指标。

1. 基本概念

核心概念：集中趋势、离散程度、分布形状

直观理解：

• 集中趋势 = 数据的"中心"在哪里
• 离散程度 = 数据"分散"的程度
• 分布形状 = 数据"长得像什么"

关键理解：

• 均值是"平衡点"
• 方差是"平均偏差的平方"
• 偏度和峰度描述分布的"不对称性"和"尖峭度"

2. 使用方法

使用 NumPy 和 pandas 进行描述统计

import numpy as np
import pandas as pd

# 创建示例数据
data = np.random.randn(100)  # 100个标准正态分布随机数
df = pd.DataFrame(data, columns=['value'])

# 基本统计量
print("均值:", df['value'].mean())
print("中位数:", df['value'].median())
print("标准差:", df['value'].std())
print("方差:", df['value'].var())
print("最小值:", df['value'].min())
print("最大值:", df['value'].max())
print("四分位数:")
print(df['value'].quantile([0.25, 0.5, 0.75]))

# 使用 describe() 概览
print(df.describe())

使用 SciPy 计算偏度和峰度

from scipy.stats import skew, kurtosis

# 偏度和峰度
print("偏度:", skew(data))
print("峰度:", kurtosis(data))  # Fisher定义，正态分布为0

3. 应用场景

数据探索性分析（EDA）

id,age,gender,salary,department,join_date,satisfaction,is_manager
1,28,Male,55000,IT,2020-03-15,7,No
2,34,Female,72000,HR,2018-07-22,8,Yes
3,22,Male,48000,Marketing,2021-01-10,5,No
4,45,Female,95000,Finance,2015-11-05,9,Yes
5,31,Male,60000,IT,2019-09-18,6,No
6,29,Female,52000,Marketing,2020-06-30,7,No
7,38,Male,82000,Finance,2017-04-12,8,No
8,41,Female,110000,HR,2014-08-25,9,Yes
9,26,Male,49000,IT,2021-03-08,6,No
10,33,Female,78000,Marketing,2018-12-14,7,Yes
11,50,Male,120000,Finance,2012-05-20,10,Yes
12,27,Female,53000,HR,2020-09-05,5,No
13,36,Male,75000,IT,2019-01-30,8,No
14,44,Female,105000,Finance,2016-07-11,9,Yes
15,30,Male,58000,Marketing,2021-08-19,7,No
16,32,Female,68000,HR,2019-11-22,6,No
17,48,Male,115000,Finance,2013-09-08,10,Yes
18,25,Female,46000,IT,2022-02-14,4,No
19,39,Male,88000,Marketing,2018-03-27,8,Yes
20,42,Female,98000,Finance,2015-12-03,9,No

import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


def explore_data(df, column):
    """对指定列进行探索性分析"""
    print(f"=== {column} 分析 ===")
    print("样本数:", len(df))
    print("缺失值:", df[column].isnull().sum())
    print("唯一值数:", df[column].nunique())

    # 统计量
    stats = df[column].describe()
    print("\n基本统计量:")
    print(stats)

    # 可视化
    fig, axes = plt.subplots(1, 2, figsize=(10, 4))
    axes[0].hist(df[column].dropna(), bins=30, edgecolor='black')
    axes[0].set_title('分布直方图')

    axes[1].boxplot(df[column].dropna())
    axes[1].set_title('箱线图')

    plt.tight_layout()
    plt.show()


# 示例
import pandas as pd

df = pd.read_csv('data.csv')  # 假设有数据文件
explore_data(df, 'age')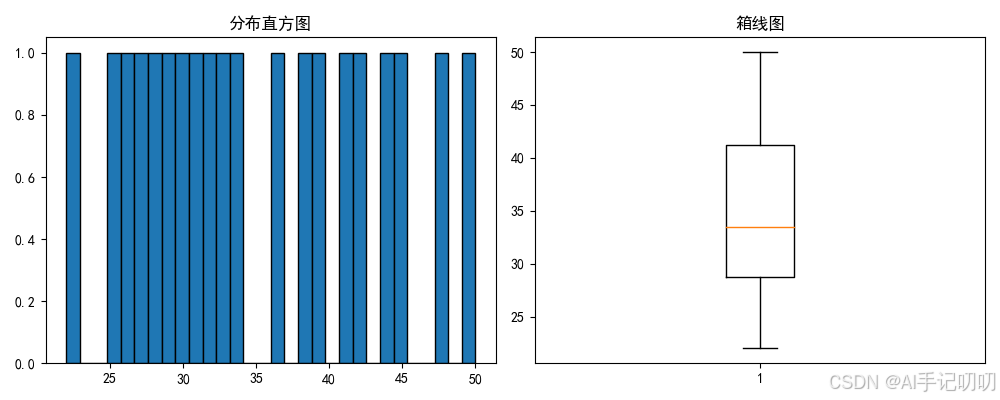

异常值检测

def detect_outliers_iqr(data, column):
    """使用IQR方法检测异常值"""
    Q1 = data[column].quantile(0.25)
    Q3 = data[column].quantile(0.75)
    IQR = Q3 - Q1
    
    lower_bound = Q1 - 1.5 * IQR
    upper_bound = Q3 + 1.5 * IQR
    
    outliers = data[(data[column] < lower_bound) | (data[column] > upper_bound)]
    return outliers, (lower_bound, upper_bound)

# 使用示例
outliers, bounds = detect_outliers_iqr(df, 'salary')
print(f"异常值数量: {len(outliers)}")
print(f"边界范围: [{bounds[0]:.2f}, {bounds[1]:.2f}]")

二、 概率运算

概率运算是研究随机现象数量规律的数学分支，为统计学提供理论基础。

概率运算的核心是"不确定性中的规律性"

1. 基本概念

核心概念：概率分布、期望、方差、条件概率、贝叶斯定理

直观理解：

• 概率分布 = 随机变量所有可能取值的"可能性地图"
• 期望 = 长期平均结果
• 条件概率 = 已知某些信息时的概率

关键理解：

• 概率是长期频率的极限
• 独立事件的概率相乘
• 贝叶斯定理是"用新证据更新信念"

2. 使用方法

使用 SciPy 处理概率分布

from scipy.stats import norm, binom, poisson, expon
import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 正态分布
mu, sigma = 0, 1
x = np.linspace(-4, 4, 100)
pdf = norm.pdf(x, mu, sigma)  # 概率密度函数
cdf = norm.cdf(x, mu, sigma)  # 累积分布函数

fig, axes = plt.subplots(1, 2, figsize=(10, 4))
axes[0].plot(x, pdf, 'b-', lw=2)
axes[0].set_title('正态分布PDF')
axes[0].grid(True)

axes[1].plot(x, cdf, 'r-', lw=2)
axes[1].set_title('正态分布CDF')
axes[1].grid(True)

plt.tight_layout()
plt.show()

# 计算概率
print("P(X ≤ 1):", norm.cdf(1, mu, sigma))
print("P(X > 1):", 1 - norm.cdf(1, mu, sigma))
print("P(-1 ≤ X ≤ 1):", norm.cdf(1, mu, sigma) - norm.cdf(-1, mu, sigma))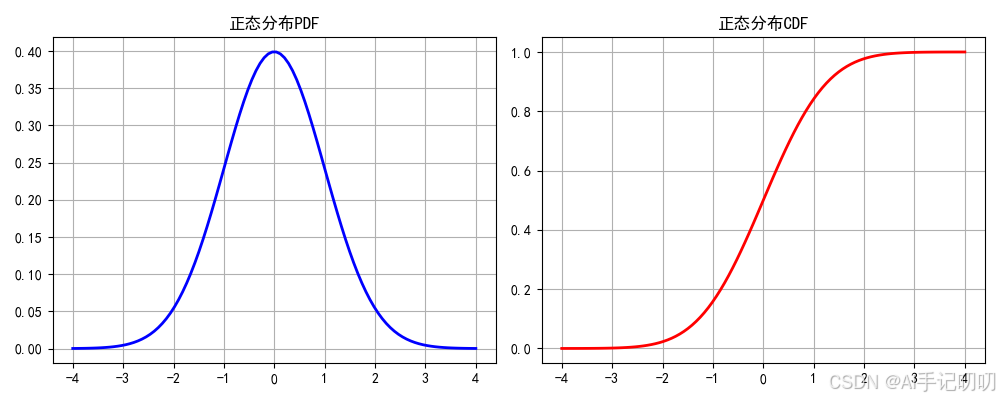

二项分布和泊松分布

from scipy.stats import norm, binom, poisson, expon
import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
n, p = 10, 0.5
k_values = np.arange(0, n + 1)
binom_probs = binom.pmf(k_values, n, p)

print("二项分布概率:")
for k, prob in zip(k_values, binom_probs):
    print(f"P(X={k}) = {prob:.4f}")

# 泊松分布
lam = 3  # 平均发生率
poisson_probs = poisson.pmf(k_values, lam)

# 可视化
fig, axes = plt.subplots(1, 2, figsize=(10, 4))
axes[0].bar(k_values, binom_probs)
axes[0].set_title(f'二项分布 B({n},{p})')

axes[1].bar(k_values, poisson_probs)
axes[1].set_title(f'泊松分布 Pois({lam})')

plt.tight_layout()
plt.show()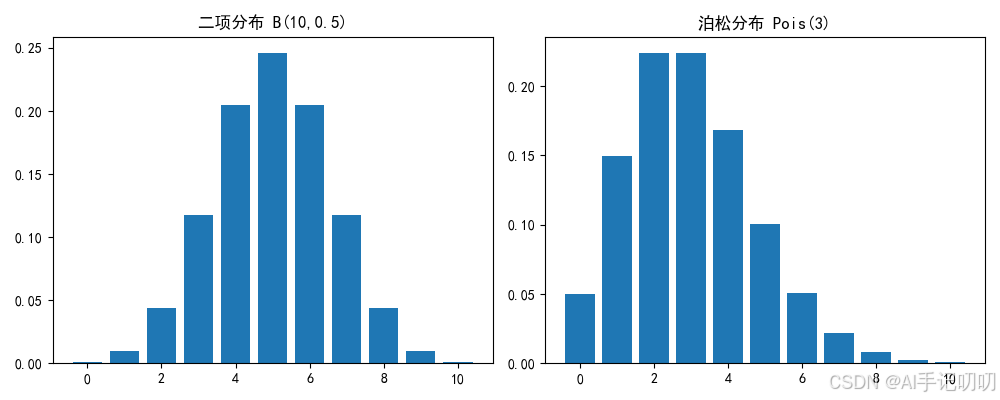

贝叶斯定理应用

def bayes_theorem(p_a, p_b_given_a, p_b_given_not_a):
    """计算 P(A|B)"""
    p_not_a = 1 - p_a
    p_b = p_b_given_a * p_a + p_b_given_not_a * p_not_a
    p_a_given_b = (p_b_given_a * p_a) / p_b
    return p_a_given_b

# 示例：疾病检测
p_disease = 0.01  # 患病率
p_positive_given_disease = 0.99  # 敏感性
p_positive_given_no_disease = 0.05  # 假阳性率

p_disease_given_positive = bayes_theorem(
    p_disease, 
    p_positive_given_disease, 
    p_positive_given_no_disease
)

print(f"检测阳性时真正患病的概率: {p_disease_given_positive:.4f}")

3. 应用场景

蒙特卡洛模拟

import numpy as np


def monte_carlo_pi(num_samples=100000):
    """用蒙特卡洛方法估计π值"""
    x = np.random.uniform(-1, 1, num_samples)
    y = np.random.uniform(-1, 1, num_samples)

    inside_circle = (x ** 2 + y ** 2) <= 1
    pi_estimate = 4 * np.sum(inside_circle) / num_samples

    return pi_estimate


# 不同样本量的估计
for n in [100, 1000, 10000, 100000]:
    pi_est = monte_carlo_pi(n)
    print(f"样本数 {n:6d}: π ≈ {pi_est:.6f} (误差: {abs(pi_est - np.pi):.6f})")

样本数    100: π ≈ 3.240000 (误差: 0.098407)
样本数   1000: π ≈ 3.040000 (误差: 0.101593)
样本数  10000: π ≈ 3.155200 (误差: 0.013607)
样本数 100000: π ≈ 3.134360 (误差: 0.007233)

风险评估

import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

def value_at_risk(returns, confidence_level=0.95):
    """计算在险价值（VaR）"""
    var = np.percentile(returns, (1 - confidence_level) * 100)
    return var

# 模拟投资回报
np.random.seed(42)
daily_returns = np.random.normal(0.001, 0.02, 1000)  # 日回报率

# 计算VaR
var_95 = value_at_risk(daily_returns, 0.95)
var_99 = value_at_risk(daily_returns, 0.99)

print(f"95%置信水平的VaR: {var_95:.4%}")
print(f"99%置信水平的VaR: {var_99:.4%}")

# 可视化
plt.hist(daily_returns, bins=50, edgecolor='black', alpha=0.7)
plt.axvline(var_95, color='red', linestyle='--', label=f'95% VaR = {var_95:.2%}')
plt.axvline(var_99, color='orange', linestyle=':', label=f'99% VaR = {var_99:.2%}')
plt.xlabel('日回报率')
plt.ylabel('频数')
plt.title('投资回报分布与VaR')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()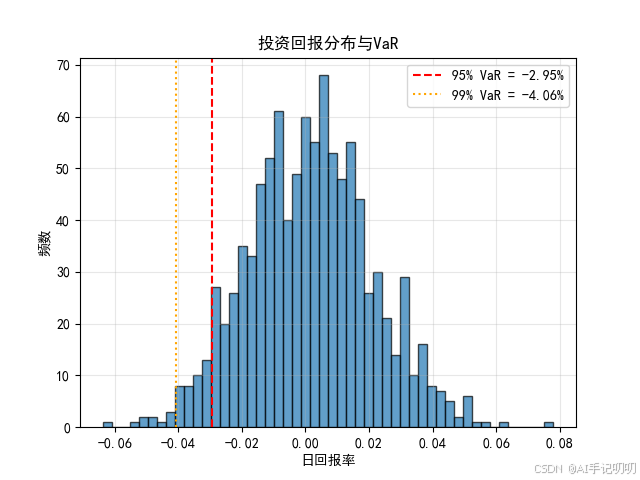

三、 总结

统计类型	主要方法	适用场景
描述统计	pandas.describe(), scipy.stats.skew()	数据探索、异常检测
概率运算	scipy.stats模块、贝叶斯公式	风险评估、蒙特卡洛模拟

基础统计用pandas，概率计算用SciPy，可视化用matplotlib/seaborn。

四、 相关文章

Python数学：幂运算与根式运算
Python数学：函数运算
Python数学：几何运算

---

鼓起勇气求关注......（悄悄点一下就好，谢谢你💐）