宽搜bfs与深搜dfs

今天这章因为期末周拖了几天，就算熬夜写也不能再拖到明天了；今日事，今日毕，最近的时间得好好安排下了/(ㄒoㄒ)/~~

宽搜

以今天写的代码展开详细描述与解释,并附上题目

cpp 复制代码

const int N = 10;
string a, b;
int n;
unordered_map<string, int> dist;
string x[N], y[N];

int bfs()
{
    if (a == b) return 0;
    queue<string> q;
    q.push(a);
    dist[a] = 0;
    while (q.size())
    {
        string s = q.front(); q.pop();
        if (dist[s] >= 10) return -1;
        for (int i = 0; i < n; i++)
        {
            int pos = 0;
            while (s.find(x[i],pos) != -1)
            {
                pos = s.find(x[i],pos);
                string tmp = s.substr(0, pos) + y[i] + s.substr(pos + x[i].size());
                pos++;//从下一个位置开始找，如若不++，就会一直死循环
                if (dist.count(tmp)) continue;
                q.push(tmp);
                dist[tmp] = dist[s] + 1;
                if (tmp == b) return dist[tmp];
            }
        }
    }
    return -1;
}

int main()
{
    cin >> a >> b;
    while (cin >> x[n] >> y[n]) n++;
    int ret = bfs();
    if (ret == -1) cout << "NO ANSWER!" << endl;
    else cout << ret << endl;
    return 0;
}

这是一道在洛谷上写的题目，所以使用全局的变量更加方便，根据输入要求，我直接把数组设置的足够大，那么就不用考虑越界的问题

题目的主要实现逻辑在于bfs函数，针对这个函数的逻辑与变量参数都要仔细理解

a代表着初始字串，b代表的是目标字串；在一进入函数之后就需要判断a是否和b完全相同，如若相同，就可以不用继续执行之后的逻辑，减小消耗

队列q：在这个算法中，队列是作用是存储在遍历字串a时，找到的所有可能的变换，存在队列q的字串中，可能有已经经过一次、两次变换不等，如若变化了十次，就需要直接返回-1，以示错误(因为当第一个10出现后，之后的字串至少为10变化，所以继续遍历毫无意义)

哈希表dist：它的第一个参数类型是string->用于存储所有的变换；第二个参数类型是int ->用于存储在某种路径下，变成字串q.front()此时所需的次数

for循环与pos变量：for循环是遍历所有变换规则，在变换出所有可能的字串；pos变量++操作是为了不让while死循环；如果pos不++，那么接口find(x[i],pos)的使用，就会一直查询同一个位子，致使while死循环

substr的使用：是用于查找在a中可能存在的变换规则，如果找到就返回当前的位置，并且更新pos；如若没找到就返回-1，并且直接跳出循环

注意：substr接口的数字接口是左闭右开的！！！

临时变量tmp：dist.count(tmp)判断的是该临时字串是否已经出现过了，如若出现过了，就跳出本次while循环(因为是出现过一次，如果再继续变换，就会重复之前的变换，使得时间复杂度大大增加，避免这种情况，直接跳出循环即可)；再把符合条件的tmp放入队列中，继续可能到达目标字串的变化

*剪枝：在函数的最后有一个if判断，如若此时的tmp就是我们所需要的目标字串，就不需要再继续遍历队列了，徒增复杂度，直接在原地返回就可以获得最终的答案了

深搜(Ⅰ---种类问题型)

以以前写的代码展开详细描述与解释,并附上题目

cpp 复制代码

const int N = 7;
int dx[4] = { 0,0,-1,1 };
int dy[4] = { -1,1,0,0 };
int a, b;
int ret = 0;
bool st[N][N];

void dfs(int i,int j)
{
    if (i < 1 || i >= a || j < 1 || j >= b)
    {
        ret++;
        return;
    }
    st[i][j] = true;
    for (int k = 0; k < 4; k++)
    {
        int x = i + dx[k], y = j + dy[k];
        if (!st[x][y])
        {
            st[x][y] = true;
            dfs(x, y);
            st[x][y] = false;
        }
    }
    st[i][j] = false;
}

int main()
{
    cin >> a >> b;
    //行
    for (int i = 1; i < a; i++)
    {
        st[i][0] = true;
        dfs(i,1);
        st[i][0] = false;
    }
    //列
    for (int j = 1; j < b; j++)
    {
        st[0][j] = true;
        dfs(1,j);
        st[0][j] = false;
    }
    cout << ret << endl;
    return 0;
}

这是一道在洛谷上写的题目，所以使用全局的变量更加方便，根据输入要求，我直接把数组设置的足够大，那么就不用考虑越界的问题

题目的主要实现逻辑在于dfs函数，针对这个函数的逻辑与变量参数都要仔细理解

本道题需要一定的问题转化能力，若单纯把它，看成一个矩形去举例，那么这道题的难度将大大增加，所以，需要把它转化成从一个起点出发，寻找合适的终点问题

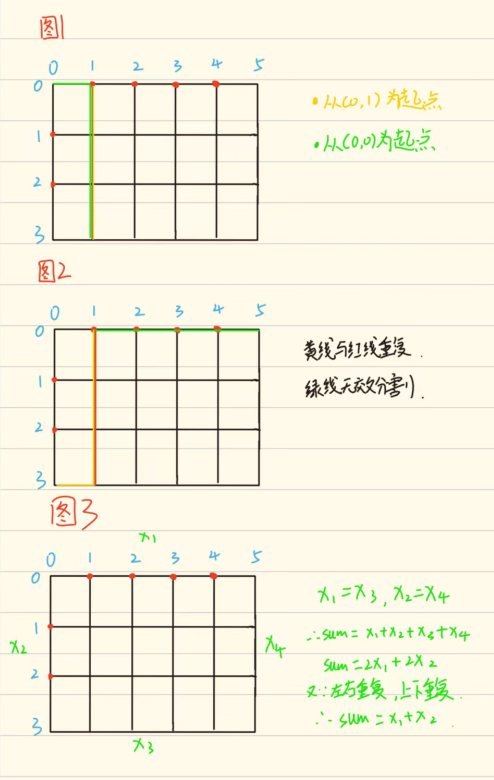
以一个3x5的矩阵为例

问题1：如何确定起点？

以(0，0)与(0，1)为例，如若分别以两个点为起点，则会出现如上图1的情况，即出现同一种情况，就会使得复杂度大大增加，不利于AC，所以我们在选取起点时不取四个顶点与方格内的点

问题二：如何确定终点？

如图二，若以四角为终点，就会出现情况重复 || 不符合规则两种情况；

同理在，选取终点时，不选四角为终点

问题三：如何优化？

如图三，由等式可知，我们从上面和下面各点为起点时各种情况重复，同理以左右面的各点为起点时方案同样相同(对称性原理)，所以看似有总共的 x1+x2+x3+x4种方案，实际上只有2x1+2x2种方案；注意：又因为左右与上下的情况完全相同，最终，总方案数=x1+x2种

细节与算法

(1)方向数组：dx与dy数组是在解决二维空间问题中常用的方法，dx[k]与dy[k] 分别对应着[i,j]这个点的上下左右这四个点(同理，也有着八个方向的数组，原理相同)

(2)bool数组st：依旧经典小连招，在递归的过程中，标记已经走过的位置，防止重复遍历，致使死循环

(3)dfs函数：是本道题的主要逻辑，在递归的过程中，找到合适的位置继续递归，在进入函数前要设置状态为true，并且在递归回来之后要恢复现场，是确保答案正确的规范操作

深搜(Ⅱ---最大/最小路径问题型)

以以前写的代码展开详细描述与解释,并附上题目

cpp 复制代码

class Solution 
{
    int dx[4]={-1,1,0,0};
    int dy[4]={0,0,-1,1};
    bool vis[101][101]={false};
    int m,n;
public:
    int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) 
    {
        int row=entrance[0];
        int col=entrance[1];
        m=maze.size(),n=maze[0].size();
        int ret=0;
        queue<pair<int,int>> q;
        q.push({row,col});
        vis[row][col]=true;
        while(q.size())
        {
           ret++;
           int sz=q.size();
           for(int i=0;i<sz;i++)
           {
            auto[a,b]=q.front();
            q.pop();
            for(int j=0;j<4;j++)
            {
                int x=a+dx[j],y=b+dy[j];
                if(x>=0 && x<m && y>=0 && y<n && maze[x][y]=='.' && !vis[x][y])
                {
                    if(x==0 || x==m-1 || y==0 || y==n-1)
                    {
                        return ret;
                    }
                    q.push({x,y});
                    vis[x][y]=true;
                }
            }
           }
        }
        return -1;
    }
};

这是一道在leetcode上写的题目，所以使用全局的变量更加方便，根据输入要求，我直接把数组设置的足够大，那么就不用考虑越界的问题

题目的主要实现逻辑在于利用队列进行层层拓展，以找到最终的结果，针对这个算法的逻辑与变量参数都要仔细理解

row与col变量：表示的是起点位于哪个位置

队列q：它的类型是pair<int,int>,是一个pair类型变量，这个类型可以同时存储两个变量(本题用于存储一对坐标，利于遍历)；对于队列本身，用于存储有效的坐标即非边界坐标与非障碍坐标；每次遇到符合条件的坐标都需要push进队列

while循环：是用于统计最终步数的主要逻辑，但是需要搭配第一个for循环使用，每次进入while循环都算是一次层拓展，即步数加1；在上一回合被放入队列的坐标，都是需要相同的步数才能达到，都是相同层；所以需要使用sz变量，在每次在提取出队列元素时，都需要将上一层的坐标全提取出来，确保答案正确性

auto[x,y]变量：结构化绑定，是c++17提出的新的语法特性；即自主推导变量类型，对于vector、pair类型等，我们就可以轻松使用(pair的第一个变量需要使用first()接口，而第二个变量需要使用second()接口)；上述代码中a表示横坐标，b表示列坐标

bool数组vis：依旧经典小连招，在递归的过程中，标记已经走过的位置，防止重复遍历，致使死循环