CCF编程能力等级认证GESP---C++7级---20251227
- [单选题(每题 2分,共 30分)](#单选题(每题 2分,共 30分))
- [判断题(每题 2分,共 20分)](#判断题(每题 2分,共 20分))
- 编程题 (每题 25分,共 50分)
-
- [3.1 编程题 1 城市规划](#3.1 编程题 1 城市规划)
- [3.2 编程题 2 学习小组](#3.2 编程题 2 学习小组)
单选题(每题 2分,共 30分)
1、下面关于C++中形参、实参和定义域的说法中,正确的一项是( )。
cpp
A.形参是函数定义时所指定的变量,它只在函数内部有效。
B.在函数内部,可以修改传入的形参的值,即使该形参是一个常量引用。
C.实参和形参的类型必须完全一致,否则会导致编译错误。
D.使用指针作为形参时,形参是指向实参的地址,因此对该指针赋值会影响实参。正确答案:A
2、已知三个序列: s1 = {3, 1, 8, 2, 5, 6, 7, 4} , s2 = {1, 5, 1, 8, 6, 4, 7, 5, 6} , s3 = {1, 8, 3, 5, 7, 6, 2, 4} 。以下哪个序列是它们的最长公共子序列( )。
cpp
A. {1, 8, 5, 6}
B. {1, 5, 6, 7}
C. {1, 8, 6}
D. {1, 5, 7, 4}正确答案:A
3、现有一个地址区间为0 ~ 10的哈希表,当出现冲突情况,会往后找第一个空的地址存储(到10冲突了就从0开始往后),现在要依次存储(1,3,5,7,9) ,哈希函数为 h ( x ) = ( x 2 + x ) m o d 11 h(x) = (x^2 + x) mod 11 h(x)=(x2+x)mod11。其中9存储在哈希表哪个地址中 ( )。
cpp
A.1
B.2
C.3
D.4正确答案:D
4、在0/1背包问题中,给定一组物品,每个物品有一个重量和价值,背包的容量有限。假设背包的最大容量为w,物品的数量为n,其中第 个物品的重量为w[i],价值为v[i]。以下关于0/1背包问题的描述,正确的是( )。
cpp
A.在解决0/1背包问题时,使用贪心算法可以保证找到最优解,因为物品只能放入一次。
B. 0/1背包是P问题(多项式时间可解问题),它可以在 的时间复杂度内解决。
C. 0/1背包问题中,动态规划解法的空间复杂度为 ,但可以通过滚动数组技巧将空间复杂度优化到 。
D. 0/1背包问题中,每个物品只能选择一次,并且子问题之间是独立的,无法重用计算结果。正确答案:C
5、一棵深度为6(根节点深度为1)的完全二叉树,节点总数最少有( )。
cpp
A. 31
B. 32
C. 63
D. 64正确答案:B
6、对于如下二叉树,下面关于访问的顺序说法错误的是( )。
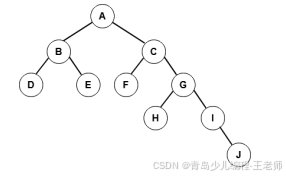
cpp
A. D E B F H J I G C A 是它的后序遍历序列。
B. A B C D E F G H I J 是它的广度优先遍历序列。
C. A B D E C F G H I J 是它的先序遍历序列。
D. D B E A F C H G J I 是它的中序遍历序列。正确答案:C
7、下面程序的运行结果为( )。
cpp
#include <iostream>
int query(int n, int *a, int x) {
int l = 0, r = n;
while (l < r) {
int mid = l + (r - l) / 2;
if (a[mid] >= x) r = mid;
else l = mid + 1;
}
if (l == n) return -1;
return l;
}
int main() {
int n = 10;
int x = 3;
int num[] = {1, 2, 2, 3, 3, 4, 5, 5, 6, 7};
std::cout << query(n, num, x) << "\n";
return 0;
}
cpp
A. 2
B. 3
C. 4
D. 5正确答案:C
8、下面程序中,函数 query 的时间复杂度是( )。
cpp
#include <iostream>
int query(int n, int *a, int x) {
int l = 0, r = n;
while (l < r) {
int mid = l + (r l) / 2;
if (a[mid] >= x) r = mid;
else l = mid + 1;
}
if (l == n) return -1;
return l;
}
int main() {
int n = 10;
int x = 3;
int num[] = {1, 2, 2, 3, 3, 4, 5, 5, 6, 7};
std::cout << query(n, num, x) << "\n";
return 0;
}
cpp
A.O(1)
B.O(logn)
C.O(n)
D.O(nlogn)正确答案:无
9、有5个字符,它们出现的次数分别为2次、2次、3次、3次、5次。现在要用哈夫曼编码的方式来为这些字符进 行编码,最小加权路径长度WPL(每个字符的出现次数 它的编码长度,再把每个字符结果加起来)的值为( )。
cpp
A. 30
B. 34
C. 43
D. 47正确答案:B
10、下面程序的运行结果为( )。
cpp
#include <iostream>
using namespace std;
int f(int n) {
if (n <= 2) return n * 2;
return f(n - 1) + f(n - 2);
}
int main() {
cout << f(5) << endl;
return 0;
}
cpp
A. 10
B. 16
C. 26
D. 30正确答案:C
11、一个简单无向图 有36条边,且每个顶点的度数都为4,则图 的顶点个数为( )。
cpp
A. 9
B. 12
C. 18
D. 36正确答案:C
12、下面关于二叉树的说法正确的是( )。
cpp
A.任意二叉树的中序遍历与后序遍历必定不相同。
B.对任意二叉树,若已知先序遍历与后序遍历,则该二叉树唯一确定。
C.若二叉树有 个结点,根节点高度为 ,则其高度满足:
D.在二叉树的先序遍历中,根后紧跟的结点一定是根的左孩子。正确答案:无
13、假设一个算法时间复杂度的递推式是 ( 为正整数),和 ,那么这个算法的 时间复杂度是( )。
A. O ( n n ) O(n\sqrt{n}) O(nn )
B. O ( n n l o g n ) O(n\sqrt{n}logn) O(nn logn)
C. O ( n 2 ) O(n^2) O(n2)
D. O ( n 2 l o g n ) O(n^2logn) O(n2logn)
正确答案:无
14、下面哪一个可能是下图的深度优先遍历序列( )。
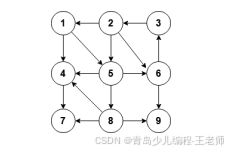
cpp
A. 1, 5, 6, 3, 2, 8, 9, 4, 7
B. 1, 5, 8, 9, 7, 4, 6, 3, 2
C. 3, 2, 1, 4, 7, 6, 9, 5, 8
D. 2, 5, 6, 3, 8, 7, 9, 4, 1正确答案:A
15、下面这个有向图的强连通分量的个数是( )。
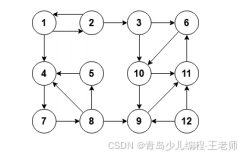
cpp
A. 3
B. 4
C. 5
D. 6正确答案:A
判断题(每题 2分,共 20分)
1、C++语言中,表达式 3 ^ 2 的结果类型为 int ,值为 9 。( )
正确答案:错误
2、使用 cmath 头文件中的正弦函数,表达式 sin(90) 的结果类型为 double ,值约为 1.0 。( )
正确答案:错误
3、使用 strcmp("10", "9") 比较两个字符串,返回值大于0,说明 "10" 比 "9" 大。( )
正确答案:错误
4、选择排序是一种不稳定的排序算法,而冒泡排序是一种稳定的排序算法。( )
正确答案:正确
5、求两个长度为 序列的最长公共子序列(LCS)长度时,可以使用滚动数组将空间复杂度从 O ( n 2 ) O(n^2) O(n2)优化到 O ( n ) O(n) O(n) 。( )
正确答案:正确
6、在无向图中,所有顶点的度数之和等于边数的两倍。( )
正确答案:正确
7、使用邻接矩阵存储一个有V个顶点、E条边的图,对该图进行一次完整的BFS遍历,时间复杂度为 O ( V + E ) O(V+E) O(V+E)。( )
正确答案:错误
8、在图像处理或游戏开发中,泛洪(flood fill)算法既可以用BFS实现,也可以用DFS实现。( )
正确答案:正确
9、使用链地址法处理冲突的哈希表,当所有元素都映射到同一个槽位时,查找操作的最坏时间复杂度为O(n), 其中 为元素个数。( )
正确答案:正确
10、一个包含V个顶点的连通无向图,其任何一棵生成树都恰好包含V-1条边。( )
正确答案:正确
编程题 (每题 25分,共 50分)
3.1 编程题 1 城市规划
【问题描述】
A国有 座城市,城市之间由 条双向道路连接,任意一座城市均可经过若干条双向道路到达另一座城市。城市依 次以 编号。第 ( )条双向道路连接城市 与城市 。
对于城市 和城市 而言,它们之间的连通度 定义为从城市 出发到达城市 所需经过的双向道路的最少条 数。由于道路是双向的,可以知道连通度满足 ,特殊地有 。
现在 A国正在规划城市建设方案。城市 的建设难度为它到其它城市的最大连通度。请你求出建设难度最小的城 市,如果有多个满足条件的城市,则选取其中编号最小的城市。形式化地,你需要求出使得 最小的 ,若存在多个可能的 则选取其中最小的。
【输入格式】
第一行,两个正整数 ,表示 A国的城市数量与双向道路数量。
接下来 行,每行两个整数 ,表示一条连接城市 与城市 的双向道路。
【输出格式】
输出一行,一个整数,表示建设难度最小的城市编号。如果有多个满足条件的城市,则选取其中编号最小的城市。
【样例输入 1】
3 3
1 2
1 3
2 3【样例输出 1】
1【样例输入 2】
4 4
1 2
2 3
3 4
2 4【样例输出 2】
1【数据范围】
对于 的测试点,保证 。
对于所有测试点,保证 , , 。
【参考程序】
cpp
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 2005;
int n, m;
vector<int> e[N];
int d[N], mx[N], q[N];
void bfs(int u) {
for (int i = 1; i <= n; i++) d[i] = n + 1;
d[u] = 0;
q[1] = u;
int ql = 1, qr = 1;
while (ql <= qr) {
int x = q[ql++];
for (auto y : e[x])
if (d[x] + 1 < d[y]) {
d[y] = d[x] + 1;
q[++qr] = y;
}
}
mx[u] = d[q[qr]];
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int u, v;
scanf("%d%d", &u, &v);
e[u].emplace_back(v);
e[v].emplace_back(u);
}
int ans = 1;
for (int i = 1; i <= n; i++) {
bfs(i);
if (mx[i] < mx[ans]) ans = i;
}
printf("%d\n", ans);
return 0;
}3.2 编程题 2 学习小组
【问题描述】
班主任计划将班级里的 名同学划分为若干个学习小组,每名同学都需要分入某一个学习小组中。班级里的同学依 次以 编号,第 名同学有其发言积极度 。
观察发现,如果一个学习小组中恰好包含编号为 的 名同学,则该学习小组的基础讨论积极度为 , 综合讨论积极度为 ,也即基础讨论积极度加上小组内同学的最大 发言积极度与最小发言积极度之差。
给定基础讨论积极度 ,请你计算将这 名同学划分为学习小组的所有可能方案中,综合讨论积极度之 和的最大值。
【输入格式】
第一行,一个正整数 ,表示班级人数。
第二行, 个非负整数 ,表示每位同学的发言积极度。
第三行, 个非负整数 ,表示不同人数学习小组的基础讨论积极度。
【输出格式】
输出一行,一个整数,表示所有划分方案中,学习小组综合讨论积极度之和的最大值。
【样例输入 1】
4
2 1 3 2
1 5 6 3【样例输出 1】
12【样例输入 2】
8
1 3 2 4 3 5 4 6
0 2 5 6 4 3 3 4【样例输出 2】
21【数据范围】
对于 的测试点,保证 。
对于所有测试点,保证 , , 。
【参考程序】
cpp
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 305;
int n;
int c[N], a[N];
int f[N][N];
int ans;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &c[i]);
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
sort(c + 1, c + n + 1);
for (int i = n; i >= 1; i--)
for (int j = 1; j <= n; j++)
for (int k = i; k <= n; k++) {
int diff = 0;
if (i > 1)
diff = c[n j + 1] c[j];
f[j][k] = max(f[j][k], f[j 1][k i] + a[i] + diff);
if (k == n)
ans = max(ans, f[j][k]);
}
printf("%d\n", ans);
return 0;
}