大数据-200 决策树信息增益详解：信息熵、ID3 选特征与 Python 最佳切分实现

TL;DR

场景：用信息熵/信息增益解释决策树为何选择某列切分，并用 Python 复现"最佳切分列"。
结论：最大化信息增益 ⇔ 最小化子节点熵的加权平均；ID3 用贪心递归构建树但易偏好多取值特征。
产出：信息增益推导脉络 + 最佳切分/按列切分/递归建树代码骨架 + 常见坑位速查。

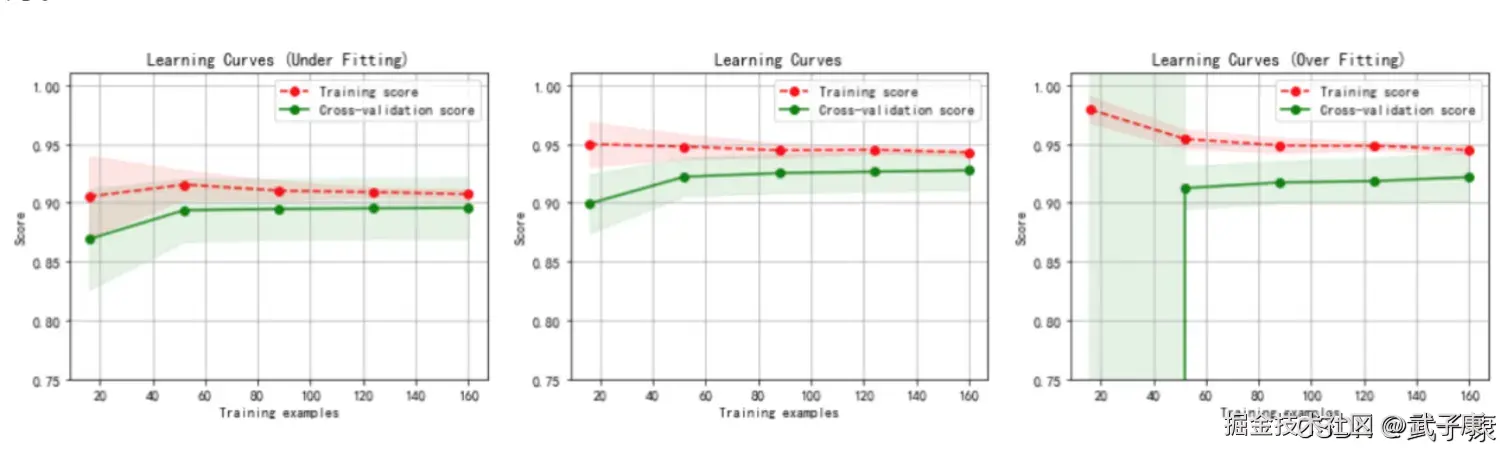
信息增益

决策树最终的优化目标使得叶节点的总不纯度最低，即对应衡量不纯度的指标最低。同时我们知道，全局最优树没有办法简单高效的获得，因此此处我们仍然要以局部最优方法来指导建模过程，并通过优化条件的设置，最终在每一步都是局部最优的条件下逐步接近最可能的全局最优解的结果。而在信息熵指数的指导下，决策树生成过程的局部最优条件也非常好理解：即在选取属性测试条件（attribute test condition）对某节点（数据集）进行切分的时候，尽可能选取使得该节点对应的子节点信息熵最小的特征进行切分。换言之，就是要求父节点信息熵和子节点信息熵之差要最大。

也可以用以下公式：

决策树归纳算法通常选择最大化增益的测试条件，因为对所有的测试条件来说，Ent（D）是一个不变的值，所以最大化增益等价于最小化分支节点的不纯性度量的加权平均值。最后，当选择熵作为公式的不纯性度量时，熵的差就是所谓的"信息增益"，即资讯获利（information gain）。

划分数据集

分类算法除了需要测量信息熵，还需要对数据集进行有效的划分。信息熵是衡量数据集纯度的重要指标，而数据集划分则是构建决策树的关键步骤。

在了解如何计算信息熵之后，我们可以采用信息增益的方法来评估数据集划分的质量。具体步骤如下：

计算当前数据集的总信息熵
对每个候选特征进行以下操作：
- 按照该特征的可能取值将数据集划分为若干子集
- 计算每个子集的信息熵
- 计算划分后的加权平均信息熵
- 计算该特征的信息增益（总信息熵 - 加权平均信息熵）

例如，在判断是否批准贷款的数据集中，可能包含"收入"、"信用记录"等特征。我们需要：

计算原始数据集的信息熵
对"收入"特征：按高、中、低划分数据集，分别计算各子集的信息熵
对"信用记录"特征：按良好、一般、差划分数据集，分别计算各子集的信息熵
比较各特征的信息增益，选择增益最大的特征作为最优划分标准

通过这种基于信息增益的特征选择方法，我们可以确定最佳的划分方式，从而构建出高效的决策树模型。在实际应用中，这种方法被广泛用于客户分类、医疗诊断、风险评估等多个领域。

数据集最佳切分函数

划分数据集的最大准则是选择最大信息增益，也就是信息下降最快的方向。通过手动计算，我们知道：

第 0 列的信息增益为 0.42，第 1 列的信息增益为 0.17
所以我们应该选择第 0 列进行切分数据集

用 Python 可以通过以下代码来输出每一列的信息增益（了解即可）：

python 复制代码

# 定义信息熵
def calEnt(dataSet):
    n = dataSet.shape[0]  # 数据集总行数
    iset = dataSet.iloc[:, -1].value_counts()  # 统计标签的所有类别
    p = iset / n  # 统计每一类标签所占比例
    ent = (-p * np.log2(p)).sum()  # 计算信息熵
    return ent

# 选择最优的列进行切分
def bestSplit(dataSet):
    baseEnt = calEnt(dataSet)  # 计算原始熵
    bestGain = 0  # 初始化信息增益
    axis = -1  # 初始化最佳切分列

    for i in range(dataSet.shape[1] - 1):  # 对特征的每一列进行循环
        levels = dataSet.iloc[:, i].value_counts().index  # 提取出当前列的所有取值
        ents = 0  # 初始化子节点的信息熵

        for j in levels:  # 对当前列的每一个取值进行循环
            childSet = dataSet[dataSet.iloc[:, i] == j]  # 某一个子节点的 dataframe
            ent = calEnt(childSet)  # 计算某一个子节点的信息熵
            ents += (childSet.shape[0] / dataSet.shape[0]) * ent  # 计算当前列的信息熵

        print('第{}列的信息熵为{}'.format(i, ents))
        infoGain = baseEnt - ents  # 计算当前列的信息增益
        print('第{}列的信息增益为{}\n'.format(i, infoGain))

        if infoGain > bestGain:
            bestGain = infoGain  # 选择最大信息增益
            axis = i  # 最大信息增益所在列的索引

    print("第{}列为最优切分列".format(axis))
    return axis

接下来我们验证构造的数据集最佳切分函数返回的结果与手动计算的结果是否一致：

python 复制代码

bestSplit(dataSet)

执行结果如下所示：

也就是说，最大信息熵的所选的特征是分类后熵值最小的特征。分类后熵值最小的特征恰恰是分类结果一致的特征，而分类结果一致的特征必须是两类样本差异最大的特征。

按照给定列切分数据集

通过最佳切分函数返回最佳切分列的索引，我们就可以根据这个索引，构建一个按照给定列切分数据集的函数。

python 复制代码

"""
函数功能：按照给定的列划分数据集
参数说明：
dataSet：原始数据集
axis：指定的列索引
value：指定的属性值
return：redataSet：按照指定列索引和属性值切分后的数据集
"""
def mySplit(dataSet, axis, value):
    col = dataSet.columns[axis]
    redataSet = dataSet.loc[dataSet[col] == value, :].drop(col, axis=1)
    return redataSet

# 验证函数：以 axis=0，value=1 为例
mySplit(dataSet, 0, 1)

执行结果如下图所示：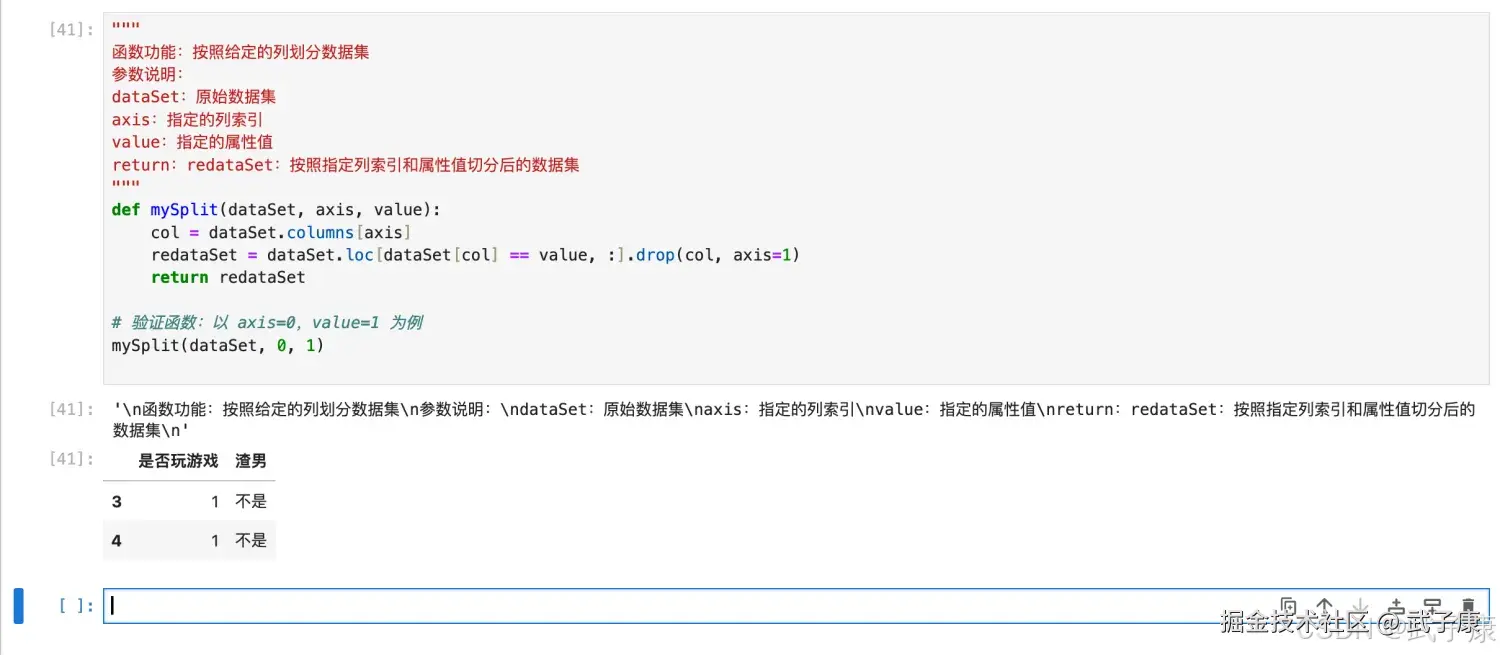

决策树的生成

目前我们已经学习了从数据集构造决策树算法所需要的子功能模块，其工作原理如下：

得到原始数据集，然后基于最好的属性值划分数据集，由于特征可能多于两个，因此可能存在大于两个分支的数据集划分
第一次划分之后，数据集被向下传递到树的分支的下一个节点
在新的节点上，我们可以再次划分数据，因此我们可以采用递归的原则处理数据集。

递归约束的条件是：

程序遍历完所有划分数据集的属性
每个分支下的所有实例都有相同的分类
当前节点包含的样本合集为空，不能划分

在第 2 种情形下，我们把当前节点标记为叶节点，并将其类别设定为该节点所含样本最多的类别，任何到达叶节点的数据必然属于叶节点的分类。在第 3 种情形下，同样把当前节点标记为叶节点，但将其类别设定为其父节点所含样本最多的类别。

ID3算法

ID3 算法原型最早由 J.R. Quinlan 在其1986年的博士论文《Induction of Decision Trees》中提出，这是第一个真正意义上完整、系统的决策树学习算法。该算法基于信息论中的信息增益准则，采用自顶向下的贪心策略递归构建决策树，其理论基础扎实，实现简单直观，因此在机器学习领域获得了广泛应用。

ID3 算法的核心思想是：在决策树的每个非叶节点上，选择当前信息增益最大的属性作为划分标准。具体计算过程如下：

计算数据集的初始熵 H(S)
对每个候选属性 A，计算其信息增益 Gain(S,A) = H(S) - Σ(|Sv|/|S|)*H(Sv)
选择信息增益最大的属性作为当前节点的划分属性
对每个属性值分支递归执行上述过程

然而，ID3 算法存在几个明显缺陷：

倾向于选择取值较多的属性（如"ID"这种唯一标识符）
不能处理连续值属性
没有考虑过拟合问题
不能处理缺失值

针对这些问题，Quinlan 在1993年提出了改进的 C4.5 算法，主要改进包括：

引入增益率（Gain Ratio）替代信息增益，解决属性偏向问题
增加了对连续值属性的处理能力
采用后剪枝策略防止过拟合
增加了对缺失值的处理机制

后续在1998年，Quinlan 又推出了 C5.0 商业版本，进一步提高了算法效率和可扩展性。这种算法演进路径展示了决策树技术从理论到实践的逐步完善过程，也体现了机器学习算法在解决实际问题时的持续优化需求。

ID3 算法的核心是决策树各个节点应用信息增益准则选择特征，递归的构建决策树。具体方法是：

从根节点开始，对节点计算所有可能的特征的信息增益。
选择信息增益最大的特征作为节点的特征，由该特征的不同取值建立子节点。
再对子节点调用以上方法，构建决策树。
直到所有特征的信息增益均很小或没有特征可以选择为止，最后得到一颗决策树。

具体 Python 的代码实现（了解即可）：

python 复制代码

"""
函数功能：基于最大信息增益切分数据集，递归构建决策树
参数说明：
dataSet：原始数据集(最后一列是标签)
return：myTree：字典形式的树
"""
def createTree(dataSet):
    featlist = list(dataSet.columns)  # 提取出数据集所有的列
    classlist = dataSet.iloc[:, -1].value_counts()  # 获取最后一列类标签
    
    # 判断最多标签数目是否等于数据集行数，或者数据集是否只有一列
    if classlist.iloc[0] == dataSet.shape[0] or dataSet.shape[1] == 1:
        return classlist.index[0]  # 如果是，返回类标签
    
    axis = bestSplit(dataSet)  # 确定当前最佳切分列的索引
    bestfeat = featlist[axis]  # 获取该索引对应的特征
    myTree = {bestfeat: {}}  # 采用字典嵌套的方式存储树信息
    
    del featlist[axis]  # 删除当前特征
    valuelist = set(dataSet.iloc[:, axis])  # 提取最佳切分列所有属性值
    
    # 对每一个属性值递归建树
    for value in valuelist:
        myTree[bestfeat][value] = createTree(mySplit(dataSet, axis, value))
    
    return myTree


# 查看运行结果
myTree = createTree(dataSet)
print(myTree)

执行结果如下所示：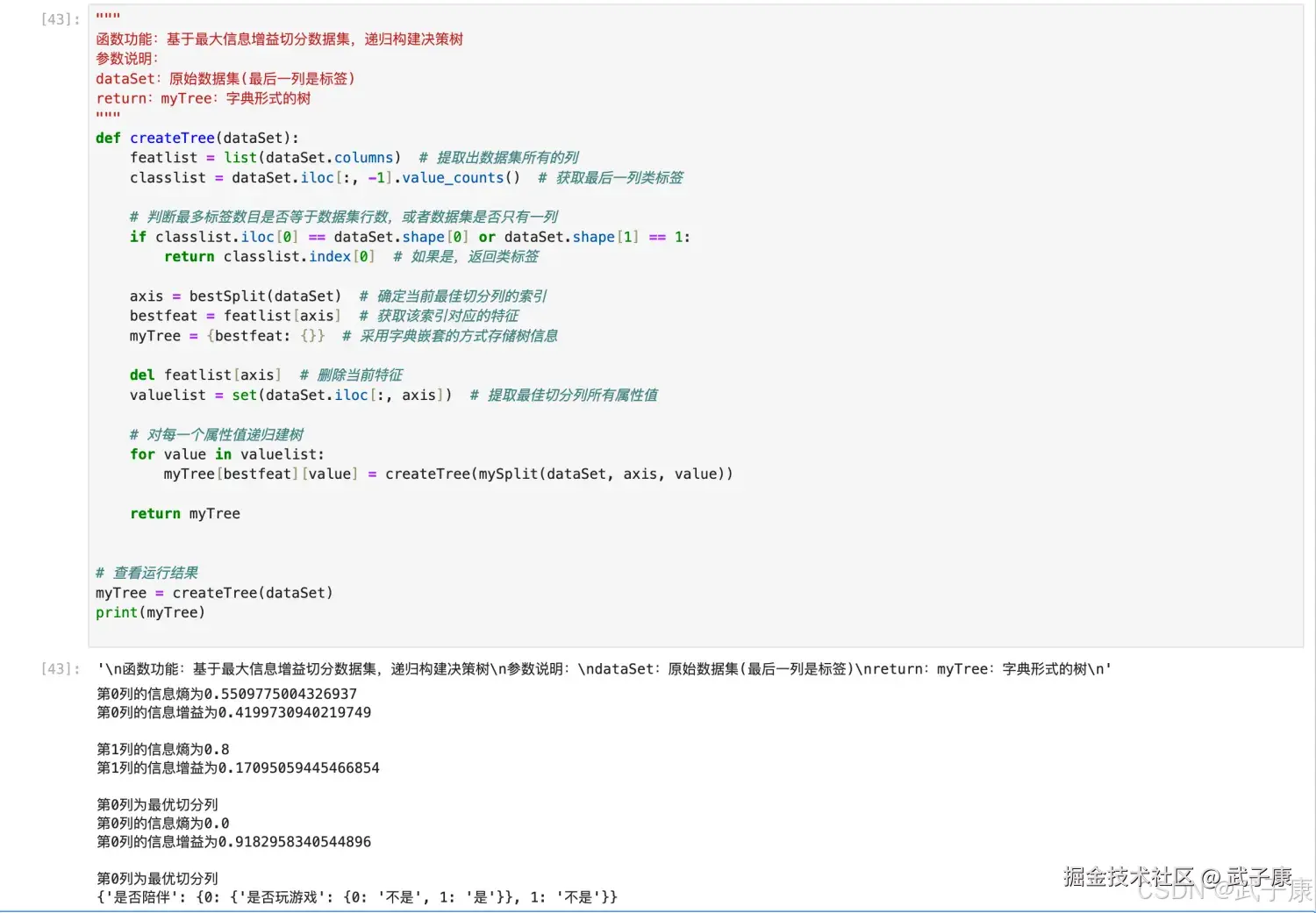

ID3算法局限性

ID3 算法的局限性主要源于局部最优化条件，即信息增益的计算方法，其局限性主要是以下几点：

分支度越高（分类水平越多）的离散变量往往子节点的总信息熵更小，ID3 是按照某一列进行切分，有一些列的分类可能不会对结果有足够好的指示。极端情况下取 ID 作为切分字段，每个分类的纯度都是 100%，因此这样的分类方式是没有效益的。
不能直接处理连续型变量，若要使用 ID3 处理联系型变量，则首先需要对连续变量进行离散化。
对缺失值较为敏感，使用 ID3 之前需要提前对缺失值进行处理。
没有剪枝的设置，容易导致过拟合，即在训练集上表现很好，测试集上表现很差

对于 ID3 的储多优化措施，最终也构成了 C4.5 算法的核心内容。

C4.5算法

C4.5 算法与 ID3 算法相似，C4.5 算法对 ID3 算法进行了改进，C4.5 在生成的过程中，用信息增益比准则来选择特征

错误速查

症状	根因	定位	修复
熵计算得到 nan 或 inf	概率为 0 时 log2(0)	calEnt() 中 p 是否出现 0	过滤 0 概率：p = p[p>0] 后再算；或加极小值 eps
信息增益全为 0/很小	标签列选错、数据被错误过滤导致熵不变	dataSet.iloc[:, -1] 是否真是标签；子集是否为空	明确标签列；检查 childSet.shape[0]；空子集跳过
bestSplit 输出列不稳定	set() 遍历无序、value_counts().index 顺序影响打印观感	levels、valuelist 的来源	用 sorted(levels) 保持确定性；树分支也用排序
drop(..., axis=1) 报参数错误/告警	pandas 版本差异或传参习惯不一致	drop(col, axis=1) 处固定写法	drop(columns=[col])
递归建树后结果异常深/过拟合	无剪枝、离散取值多导致分支爆炸	createTree() 每层划分分支数	引入最小样本数/最大深度/信息增益阈值；或切换 C4.5/剪枝策略
取"ID列/唯一值列"作为最佳特征	信息增益偏好多取值属性	观察某列取值数量远大于其他列	用增益率（C4.5）或预先剔除高基数标识列
连续值特征无法处理	代码按离散取值划分levels = value_counts().index 直接枚举	连续特征	先分箱离散化；或实现阈值切分（排序+枚举切点）

其他系列

🚀 AI篇持续更新中（长期更新）

AI炼丹日志-29 - 字节跳动 DeerFlow 深度研究框斜体样式架私有部署测试上手架构研究 ，持续打造实用AI工具指南！ AI研究-132 Java 生态前沿 2025：Spring、Quarkus、GraalVM、CRaC 与云原生落地

💻 Java篇持续更新中（长期更新）

Java-207 RabbitMQ Direct 交换器路由：RoutingKey 精确匹配、队列多绑定与日志分流实战 MyBatis 已完结，Spring 已完结，Nginx已完结，Tomcat已完结，分布式服务已完结，Dubbo已完结，MySQL已完结，MongoDB已完结，Neo4j已完结，FastDFS 已完结，OSS已完结，GuavaCache已完结，EVCache已完结，RabbitMQ正在更新... 深入浅出助你打牢基础！

📊 大数据板块已完成多项干货更新（300篇）：

包括 Hadoop、Hive、Kafka、Flink、ClickHouse、Elasticsearch 等二十余项核心组件，覆盖离线+实时数仓全栈！ 大数据-278 Spark MLib - 基础介绍机器学习算法梯度提升树 GBDT案例详解