储备池计算基础实践

TonyLee0172026-01-03 11:26

储备池计算在复杂系统建模方面有不少应用，尤其是对于那些数据样本量小的情况。这里记录一下储备池计算的基本内容以及初步的工程实践。

1. 什么是储备池？

  1. 基本定义：储备池计算通常用于储备池计算（Reservoir Computing, RC） 模型，这是一种基于递归神经网络（RNN）的简化深度学习框架，核心是利用一个随机生成、固定不变的储备池（Reservoir） 来捕捉输入序列的动态特征，仅训练输出层的连接权重。

    RC这个领域是由两篇twin paper共同确立的，这两篇paper一个从Engineering的角度提出了Echo State Network的概念，另一个从bio的角度提出了Liquid State Machine的概念。这两篇paper的链接如下，有兴趣可以拿来参考：

    1. The "echo state" approach to analyzing and training recurrent neural networks（2001）
    2. Realtime computing without stable states: a new framework for neural computation based on perturbations（2002）
    3. Reservoir Computing（2021） 考虑一下调研最新进展。

  2. 基本结构 ：储备池计算包含三个核心部分：

    （1）输入层：将外部输入映射到储备池空间。

    （2）储备池：由大量随机连接的神经元组成，状态随输入序列动态变化，且内部权重固定不训练。

    （3）输出层：线性层，将储备池的状态映射到目标输出，仅训练该层权重 。

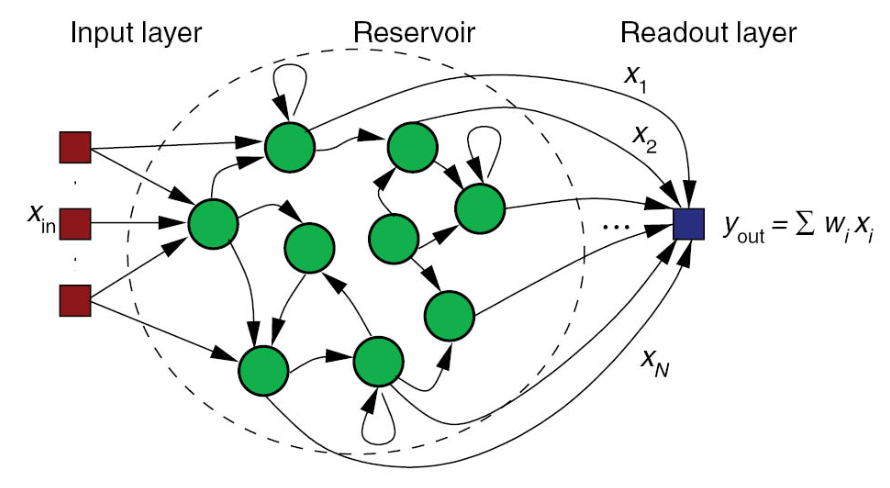
  3. 储备池状态更新公式 ：x(t)=f(Winu(t)+Wresx(t−1)+b)\mathbf{x}(t) = f(\mathbf{W}{in}\mathbf{u}(t) + \mathbf{W}{res}\mathbf{x}(t-1) + \mathbf{b})x(t)=f(Winu(t)+Wresx(t−1)+b)其中各参数含义：

    • u(t)∈RNin\mathbf{u}(t) \in \mathbb{R}^{N_{in}}u(t)∈RNin：ttt时刻的输入向量，NinN_{in}Nin为输入维度。
    • x(t)∈RNres\mathbf{x}(t) \in \mathbb{R}^{N_{res}}x(t)∈RNres：ttt时刻的储备池状态向量，NresN_{res}Nres为储备池神经元数量（通常远大于输入维度）。
    • Win∈RNres×NinW_{in} \in \mathbb{R}^{N_{res} \times N_{in}}Win∈RNres×Nin：输入层到储备池的连接权重，随机生成且固定。
    • Wres∈RNres×NresW_{res} \in \mathbb{R}^{N_{res} \times N_{res}}Wres∈RNres×Nres：储备池内部神经元的连接权重，随机生成且固定，需满足回声状态特性（Echo State Property, ESP） ------ 保证状态不会发散。
    • b∈RNres\mathbf{b} \in \mathbb{R}^{N_{res}}b∈RNres：储备池神经元的偏置项，随机生成。
    • f(⋅)f(⋅)f(⋅)：神经元的激活函数，常用 tanh 或 ReLU。

  4. 输出层计算与训练

    • 输出 y(t)y(t)y(t) 是储备池状态的线性组合：y(t)=Wout⋅[x(t)u(t)]y(t) = W_{out} \cdot \left[ \begin{array}{c} x(t) \\ u(t) \end{array} \right]y(t)=Wout⋅[x(t)u(t)]其中：Wout∈RNout×(Nres+Nin)W_{out} \in \mathbb{R}^{N_{out}\times(N_{res}+N_{in})}Wout∈RNout×(Nres+Nin)为输出层权重，是唯一需要训练的参数 ，NoutN_{out}Nout为输入维度。
    • 训练目标是最小化预测输出与真实标签的误差，通常用最小二乘法求解 WoutW_{out}Wout
    • 关键约束 ：为保证储备池状态稳定、不发散，储备池内部权重WresW_{res}Wres的谱半径 （最大特征值的模）必须小于 1：ρ(Wres)<1\rho(W_{res})<1ρ(Wres)<1 这是储备池计算的核心条件，也是其区别于传统 RNN 的关键。

2. 储备池计算的实现

这里考虑使用储备池预测混沌系统作为示例，这是储备池计算最经典也最能体现其优势的应用场景 ------ 因为混沌系统对初始条件极度敏感，而 RC 的动态储备池能很好捕捉这种复杂的非线性时序特征。

具体代码如下：

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import pinv
from mpl_toolkits.mplot3d import Axes3D
import warnings
warnings.filterwarnings('ignore')  # 忽略数值计算警告

# --------------------------
# 1. 生成Lorenz系统数据（优化数值稳定性）
# --------------------------
def lorenz_system(sigma=10, beta=8/3, rho=28, dt=0.01, T=50, x0=[1, 1, 1]):
    """
    求解Lorenz方程生成时间序列（增加数值稳定性）
    参数:
        sigma, beta, rho: Lorenz系统参数
        dt: 时间步长
        T: 总时间
        x0: 初始值
    返回:
        t: 时间数组, x: 状态数组 (n_steps, 3)
    """
    n_steps = int(T / dt)
    t = np.linspace(0, T, n_steps)
    x = np.zeros((n_steps, 3), dtype=np.float64)  # 使用float64提高精度
    x[0] = x0
    
    # 龙格-库塔法(RK4)求解Lorenz方程
    for i in range(n_steps - 1):
        x1, y1, z1 = x[i]
        k1 = np.array([
            sigma * (y1 - x1),
            x1 * (rho - z1) - y1,
            x1 * y1 - beta * z1
        ], dtype=np.float64)
        
        x2, y2, z2 = x[i] + 0.5 * dt * k1
        k2 = np.array([
            sigma * (y2 - x2),
            x2 * (rho - z2) - y2,
            x2 * y2 - beta * z2
        ], dtype=np.float64)
        
        x3, y3, z3 = x[i] + 0.5 * dt * k2
        k3 = np.array([
            sigma * (y3 - x3),
            x3 * (rho - z3) - y3,
            x3 * y3 - beta * z3
        ], dtype=np.float64)
        
        x4, y4, z4 = x[i] + dt * k3
        k4 = np.array([
            sigma * (y4 - x4),
            x4 * (rho - z4) - y4,
            x4 * y4 - beta * z4
        ], dtype=np.float64)
        
        x[i+1] = x[i] + (dt / 6) * (k1 + 2*k2 + 2*k3 + k4)
    
    return t, x

# --------------------------
# 2. 储备池神经网络实现（修复维度错误）
# --------------------------
class ReservoirComputer:
    def __init__(self, input_dim, reservoir_size=500, spectral_radius=0.95, 
                 sparsity=0.1, input_scaling=1.0, leak_rate=0.8):
        """
        初始化储备池神经网络
        参数:
            input_dim: 输入维度
            reservoir_size: 储备池神经元数量
            spectral_radius: 储备池矩阵谱半径（控制混沌程度）
            sparsity: 储备池矩阵稀疏度
            input_scaling: 输入缩放因子
            leak_rate: 泄漏率 (0,1]
        """
        self.input_dim = input_dim
        self.reservoir_size = reservoir_size
        self.spectral_radius = spectral_radius
        self.sparsity = sparsity
        self.input_scaling = input_scaling
        self.leak_rate = leak_rate
        
        # 初始化储备池权重矩阵 W
        self.W = self._create_reservoir_matrix()
        # 初始化输入权重矩阵 W_in
        self.W_in = self.input_scaling * (2 * np.random.rand(reservoir_size, input_dim) - 1)
        # 输出权重矩阵（训练后赋值）
        self.W_out = None
        
    def _create_reservoir_matrix(self):
        """创建稀疏的储备池权重矩阵，并调整谱半径"""
        # 生成随机稀疏矩阵
        W = np.random.randn(self.reservoir_size, self.reservoir_size)
        mask = np.random.rand(self.reservoir_size, self.reservoir_size) < self.sparsity
        W[~mask] = 0
        
        # 调整谱半径
        eigvals = np.linalg.eigvals(W)
        max_eigval = np.max(np.abs(eigvals))
        if max_eigval != 0:  # 防止除以0
            W = W * (self.spectral_radius / max_eigval)
        
        return W
    
    def _update_reservoir(self, x, r_prev):
        """更新储备池状态"""
        r_new = np.tanh(np.dot(self.W_in, x) + np.dot(self.W, r_prev))
        r = (1 - self.leak_rate) * r_prev + self.leak_rate * r_new
        return r
    
    def train(self, X_train, y_train, reg=1e-6):
        """
        训练输出层（伪逆方法）- 修复维度匹配问题
        参数:
            X_train: 输入序列 (n_samples, input_dim)
            y_train: 目标序列 (n_samples, output_dim)
            reg: 正则化系数（防止过拟合）
        """
        # 初始化储备池状态
        r = np.zeros(self.reservoir_size, dtype=np.float64)
        # 收集储备池状态
        R = []
        
        for x in X_train:
            r = self._update_reservoir(x, r)
            R.append(r.copy())
        
        R = np.array(R, dtype=np.float64)  # (n_samples, reservoir_size)
        
        # 修复核心：正确的矩阵运算维度
        # 正确公式：W_out = (Y * R^T) * (R * R^T + reg*I)^-1  → 错误
        # 正确公式：W_out = Y^T * (R^T * R + reg*I)^-1 * R^T  → 正确
        R_T = R.T  # (reservoir_size, n_samples)
        RR_T = np.dot(R_T, R)  # (reservoir_size, reservoir_size)
        reg_term = reg * np.eye(self.reservoir_size, dtype=np.float64)
        inv_matrix = pinv(RR_T + reg_term)  # (reservoir_size, reservoir_size)
        
        # 计算输出权重 W_out: (reservoir_size, output_dim)
        self.W_out = np.dot(np.dot(inv_matrix, R_T), y_train)
        
    # def predict(self, X_init, n_steps):
    #     """
    #     多步预测
    #     参数:
    #         X_init: 初始输入 (input_dim,)
    #         n_steps: 预测步数
    #     返回:
    #         y_pred: 预测序列 (n_steps, output_dim)
    #     """
    #     if self.W_out is None:
    #         raise ValueError("模型未训练，请先调用train()方法")
        
    #     # 初始化储备池状态
    #     r = np.zeros(self.reservoir_size, dtype=np.float64)
    #     # 先用初始输入更新储备池状态
    #     r = self._update_reservoir(X_init, r)
        
    #     # 开始预测
    #     y_pred = []
    #     current_x = X_init
        
    #     for _ in range(n_steps):
    #         # 预测下一步: (output_dim,)
    #         y_step = np.dot(self.W_out.T, r)
    #         y_pred.append(y_step)
            
    #         # 更新储备池状态（用预测值作为下一次输入）
    #         current_x = y_step
    #         r = self._update_reservoir(current_x, r)
        
    #     return np.array(y_pred, dtype=np.float64)
    
    def predict_rolling(self, X_full, train_len, n_pred_steps, step_ahead=1):
        """短步滚动预测：每次只预测step_ahead步，用真实值更新状态"""
        r = np.zeros(self.reservoir_size, dtype=np.float64)
        # 用训练数据初始化储备池状态
        for x in X_full[:train_len]:
            r = self._update_reservoir(x, r)
        
        y_pred = []
        current_idx = train_len - 1
        
        for _ in range(n_pred_steps // step_ahead):
            # 预测step_ahead步
            for _ in range(step_ahead):
                y_step = np.dot(self.W_out.T, r)
                y_pred.append(y_step)
                r = self._update_reservoir(y_step, r)
            
            # 用真实值重置储备池状态（关键！修正漂移）
            current_idx += step_ahead
            if current_idx < len(X_full):
                r = np.zeros(self.reservoir_size)
                # 用真实值重新热身储备池
                for x in X_full[current_idx-20:current_idx]:
                    r = self._update_reservoir(x, r)
        
        return np.array(y_pred[:n_pred_steps])


# --------------------------
# 3. 主程序：训练和预测
# --------------------------
if __name__ == "__main__":
    # 生成Lorenz数据
    t, x = lorenz_system(dt=0.01, T=100)
    
    # 数据预处理：划分训练和测试集
    train_len = int(0.7 * len(x))  # 70% 用于训练
    X_train = x[:train_len-1]      # 输入：t时刻的状态
    y_train = x[1:train_len]       # 目标：t+1时刻的状态
    
    # 初始化储备池神经网络
    # 初始化储备池时，调整为更适合Lorenz系统的参数
    rc = ReservoirComputer(
        input_dim=3,
        reservoir_size=1000,    # 更大的储备池
        spectral_radius=0.75,   # 更低的谱半径（抑制储备池混沌）
        sparsity=0.03,          # 更稀疏的连接
        input_scaling=0.2,      # 更小的输入缩放
        leak_rate=0.95          # 接近1的泄漏率
    )
    
    # 训练模型
    print("开始训练储备池神经网络...")
    rc.train(X_train, y_train, reg=1e-6)
    
    # 多步预测
    print("开始预测...")
    n_pred_steps = len(x) - train_len  # 预测剩余30%的数据
    # y_pred = rc.predict(x[train_len-1], n_pred_steps)
    y_pred = rc.predict_rolling(x, train_len, n_pred_steps, step_ahead=3)
    
    # --------------------------
    # 4. 结果可视化
    # --------------------------
    # 时间轴
    t_train = t[:train_len]
    t_pred = t[train_len:]
    
    # 绘制x维度的对比
    plt.figure(figsize=(12, 8))
    
    # 子图1：x维度对比
    plt.subplot(3, 1, 1)
    plt.plot(t_train, x[:train_len, 0], 'b-', label='训练数据')
    plt.plot(t_pred, x[train_len:, 0], 'g-', label='真实值')
    plt.plot(t_pred, y_pred[:, 0], 'r--', label='预测值')
    plt.title('Lorenz系统x维度预测')
    plt.ylabel('x')
    plt.legend()
    
    # 子图2：y维度对比
    plt.subplot(3, 1, 2)
    plt.plot(t_train, x[:train_len, 1], 'b-')
    plt.plot(t_pred, x[train_len:, 1], 'g-')
    plt.plot(t_pred, y_pred[:, 1], 'r--')
    plt.ylabel('y')
    
    # 子图3：z维度对比
    plt.subplot(3, 1, 3)
    plt.plot(t_train, x[:train_len, 2], 'b-')
    plt.plot(t_pred, x[train_len:, 2], 'g-')
    plt.plot(t_pred, y_pred[:, 2], 'r--')
    plt.xlabel('时间 t')
    plt.ylabel('z')
    
    plt.tight_layout()
    plt.show()
    
    # 绘制3D相空间对比
    fig = plt.figure(figsize=(12, 5))
    
    # 真实值
    ax1 = fig.add_subplot(121, projection='3d')
    ax1.plot(x[train_len:, 0], x[train_len:, 1], x[train_len:, 2], 'g-')
    ax1.set_title('Lorenz系统真实轨迹')
    ax1.set_xlabel('x')
    ax1.set_ylabel('y')
    ax1.set_zlabel('z')
    
    # 预测值
    ax2 = fig.add_subplot(122, projection='3d')
    ax2.plot(y_pred[:, 0], y_pred[:, 1], y_pred[:, 2], 'r-')
    ax2.set_title('RC预测轨迹')
    ax2.set_xlabel('x')
    ax2.set_ylabel('y')
    ax2.set_zlabel('z')
    
    plt.tight_layout()
    plt.show()
    
    # 计算预测误差
    mse = np.mean((x[train_len:] - y_pred) ** 2)
    print(f"\n预测均方误差 (MSE): {mse:.6f}")
    print(f"各维度MSE: x={np.mean((x[train_len:,0]-y_pred[:,0])**2):.6f}, "
          f"y={np.mean((x[train_len:,1]-y_pred[:,1])**2):.6f}, "
          f"z={np.mean((x[train_len:,2]-y_pred[:,2])**2):.6f}")

实验结果如下：

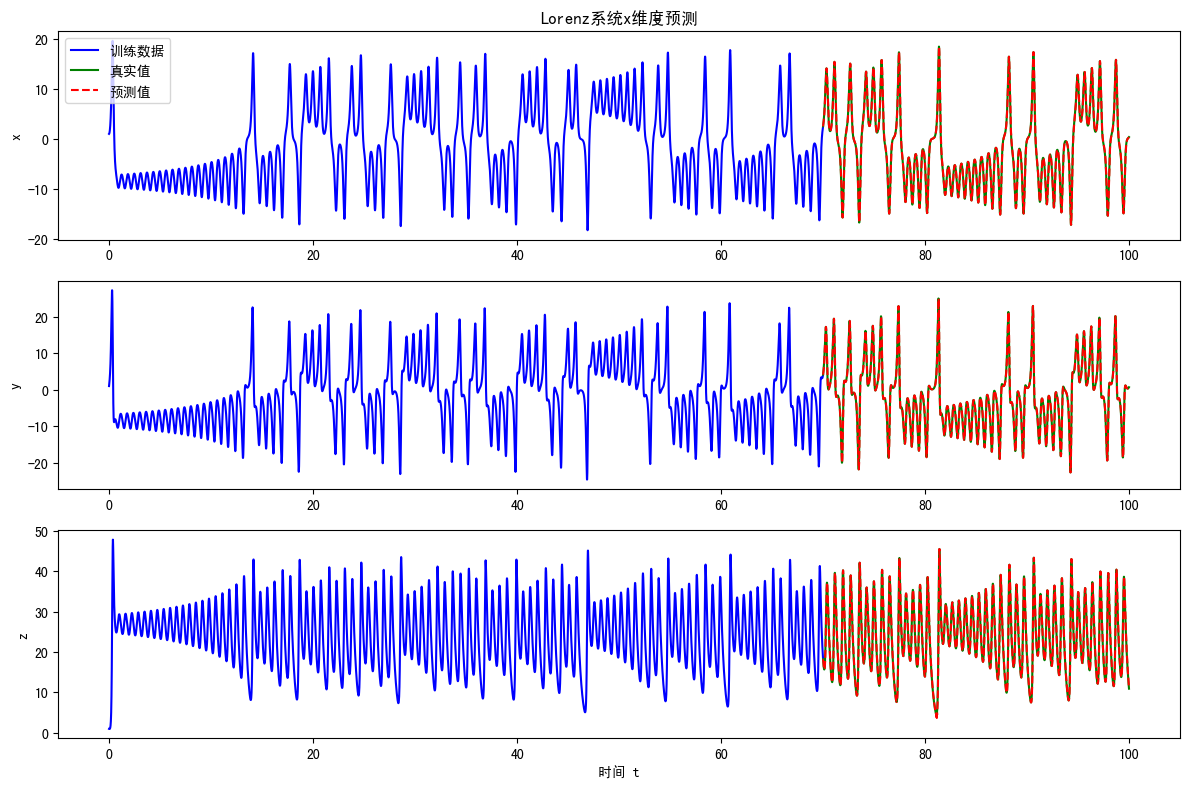
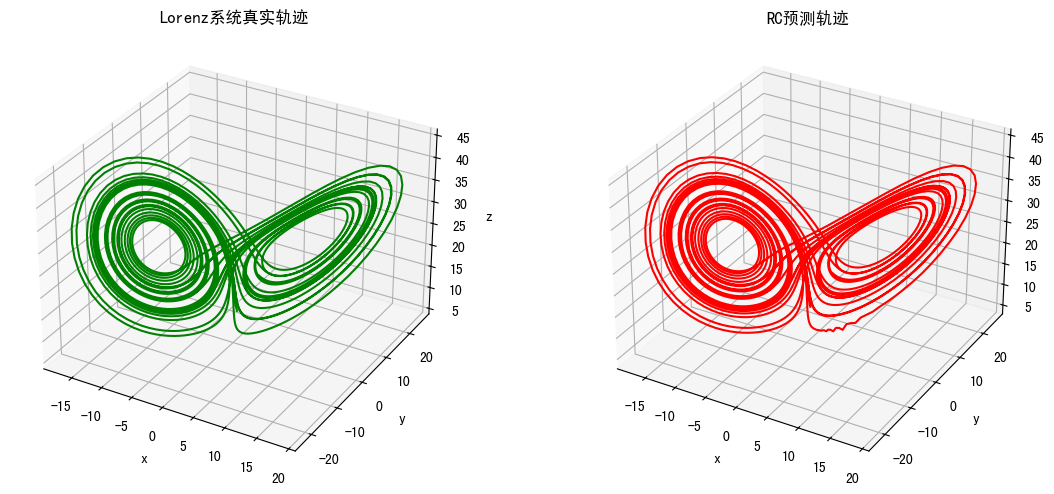
预测均方误差 (MSE): 0.395548

各维度MSE: x=0.175690, y=0.411398, z=0.599555

这里只是简单测试了一下，短期滚动预测起到了很大的提升作用，如果按照代码中predict（自主长期预测）去测试，效果其实很差。Lorenz 系统对初始误差呈指数级放大（蝴蝶效应），哪怕模型预测的第一步只有 0.001 的误差，几十步后误差就会完全掩盖真实轨迹。RC 能捕捉系统的短期动态，但无法完美复刻混沌系统的长期演化，纯自主预测会让储备池状态逐渐偏离真实状态，最终预测结果完全跑偏。

Q：短期滚动预测是否泄露信息？

这里的短步滚动预测确实用到了真实值来修正状态，这在不同场景下的 "合理性" 需要分情况讨论：

  1. 短步滚动预测的 "信息使用" 本质
    短步滚动预测中，真实值的作用是 "修正储备池状态"，而不是 "直接作为预测目标"：
  • 如果是做 "离线预测验证"（比如用历史数据测试模型效果）：这种用法是合理的，因为你只是用已知的真实值来验证模型的短期预测能力，不算信息泄露；
  • 但如果是做 "在线实时预测"（比如用当前观测值预测未来）：这种用法是完全合规的 ------ 用 "最新观测到的真实值" 来更新模型状态，再预测下一小段时间，这是工业界预测混沌系统的实际操作方式（比如气象预测就是类似逻辑）。
  1. 什么情况才算 "信息泄露"？
    如果目标是 "无真实值辅助的纯自主长期预测"（比如给定初始值后，完全不接触真实值，预测几百步），那么短步滚动预测确实不符合这个场景，但混沌系统本身就不支持这种纯自主长期预测（蝴蝶效应的本质就是 "长期不可预测"）。

简单说：混沌系统的长期预测，本身就离不开 "实时观测值的修正"，这不是信息泄露，而是这类系统预测的固有需求。

有问题欢迎交流，有错也欢迎纠正。

mingzhang23@mails.jlu.edu.cn

相关推荐
sld16832 分钟前
农资行业B2B多租户商城系统推荐，适配农业经销商层级管理
大数据·人工智能
yunhuibin32 分钟前
LeNet
人工智能·python
Mixtral2 小时前
2026年春招复盘记录工具测评：告别手动整理，AI自动生成求职总结
人工智能·面试·职场和发展·语音转文字·ai语音转文字
jaray7 小时前
PyCharm 2024.3.2 Professional 如何更换 PyPI 镜像源
ide·python·pycharm·pypi 镜像源
Psycho_MrZhang7 小时前
Neo4j Python SDK手册
开发语言·python·neo4j
Quintus五等升7 小时前
深度学习④|分类任务—VGG13
人工智能·经验分享·深度学习·神经网络·学习·机器学习·分类
2501_936146047 小时前
小型机械零件识别与分类--基于YOLO12-A2C2f-DFFN-DYT模型的创新实现
人工智能·分类·数据挖掘
web3.08889997 小时前
1688图片搜索API，相似商品精准推荐
开发语言·python
少云清8 小时前
【性能测试】15_JMeter _JMeter插件安装使用
开发语言·python·jmeter
天天讯通8 小时前
金融邀约实时质检：呼叫监控赋能客服主管
人工智能·金融
热门推荐
01GitHub 镜像站点02OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)03Claude Code Skills 实用使用手册04UV安装并设置国内源05在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）06BongoCat - 跨平台键盘猫动画工具07安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）08AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南09Linux下V2Ray安装配置指南10Open Code教程（四）| 高级配置与集成