前言
在计算机组成原理或数字逻辑设计课程中,加法器是最基础、也是最重要的算术逻辑单元之一。上一节我们通过串联多个一位全加器(Full Adder, FA),构建了一个简单的串行进位并行加法器 。这种结构虽然实现简单、易于理解,但在实际应用中存在一个致命缺陷------速度慢。
本节我们将深入探讨如何对传统加法器进行优化,引入一种更高效的设计思路:并行进位加法器(Carry Lookahead Adder, CLA)。尽管这部分内容在考试中通常不是重点,但它对于理解现代处理器中高速运算单元的设计思想具有重要意义。即使初次接触时感觉"绕",也请保持耐心------正如古人所言:"心平气和,心如止水",慢慢来,终会豁然开朗。
一、串行进位加法器的性能瓶颈
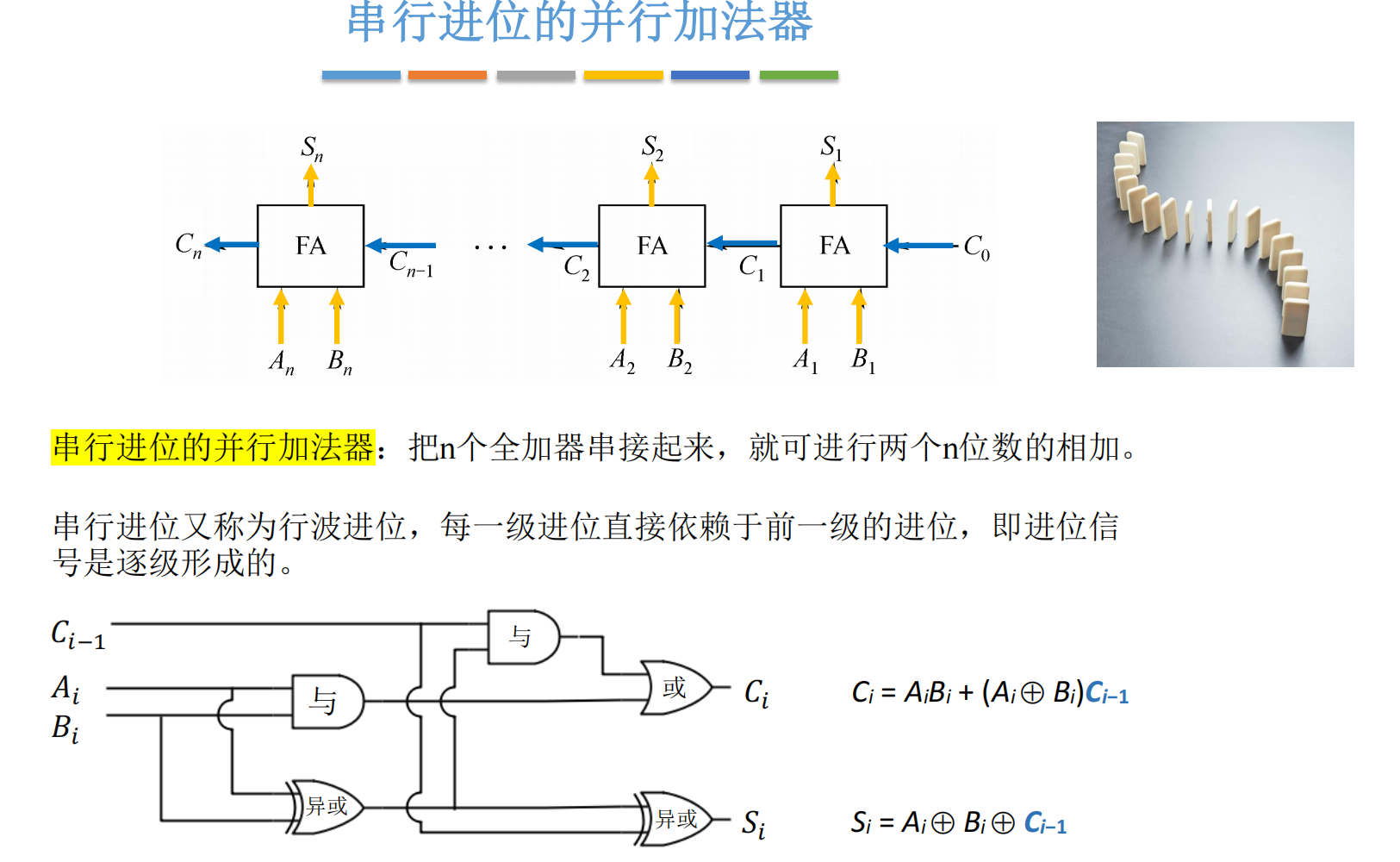
1.1 结构回顾:全加器的级联
在上一节中,我们通过将多个一位全加器首尾相连,构建了一个 n 位的并行加法器。例如,4 位加法器由 4 个 FA 依次连接而成:
- 第 0 位 FA 接收输入 a₀、b₀ 和初始进位 c₀,输出本位和 s₀ 与进位 c₁;
- 第 1 位 FA 接收 a₁、b₁ 和 c₁,输出 s₁ 与 c₂;
- ......
- 第 i 位 FA 的进位输出 c_{i+1} 依赖于前一位的进位 c_i。
这种结构看似"并行"(因为所有位同时参与运算),但实际上进位信号是串行传递的。也就是说,高位的计算必须等待低位进位结果产生后才能开始。
1.2 多米诺骨牌效应:速度受限的根本原因
想象一排多米诺骨牌:只有第一块倒下,第二块才会倒,依此类推。在串行进位加法器中,c₁ 必须先算出,c₂ 才能计算;c₂ 算出后,c₃ 才能启动......最终,第 n 位的和 s_n 要等到所有低位进位逐级传递完毕才能确定。
关键问题:加法器的整体延迟 ≈ n × 单级进位延迟。
当 n 很大时(比如 32 位、64 位),这种延迟会显著拖慢 CPU 的运算速度。因此,我们必须寻找一种方法,让高位进位不再依赖低位逐级传递,而是尽可能"提前知道"或"直接计算"出来。
二、进位生成的数学本质:递归展开与变量抽象
2.1 进位的原始表达式
一位全加器的进位输出公式为:
ci=aibi+(ai⊕bi)ci−1 c_i = a_i b_i + (a_i \oplus b_i) c_{i-1} ci=aibi+(ai⊕bi)ci−1
其中:
- aia_iai、bib_ibi 是第 i 位的加数和被加数;
- ci−1c_{i-1}ci−1 是来自低位的进位;
- "+" 表示逻辑或(OR),"·" 表示逻辑与(AND)。
这个公式告诉我们:当前位是否向更高位产生进位,取决于两个因素:
- 本位是否"自然"产生进位(即 ai=bi=1a_i = b_i = 1ai=bi=1);
- 本位是否"传递"来自低位的进位(即 ai≠bia_i \neq b_iai=bi 且 ci−1=1c_{i-1} = 1ci−1=1)。
2.2 引入抽象变量:G 与 P
为了简化分析,我们引入两个关键抽象变量:
-
生成信号(Generate) :gi=ai⋅big_i = a_i \cdot b_igi=ai⋅bi
表示第 i 位自身就能产生进位,无需依赖低位。
-
传播信号(Propagate) :pi=ai⊕bip_i = a_i \oplus b_ipi=ai⊕bi
表示第 i 位能够将低位进位传递到高位 (当 pi=1p_i = 1pi=1 时,ci=ci−1c_i = c_{i-1}ci=ci−1)。
于是,进位公式可重写为:
ci=gi+pi⋅ci−1 c_i = g_i + p_i \cdot c_{i-1} ci=gi+pi⋅ci−1
这个形式简洁而富有启发性。
2.3 递归展开:从 c₁ 到 c₄
现在,我们尝试将高位进位逐步展开,看看能否找到规律:
- c1=g1+p1c0c_1 = g_1 + p_1 c_0c1=g1+p1c0
- c2=g2+p2c1=g2+p2(g1+p1c0)=g2+p2g1+p2p1c0c_2 = g_2 + p_2 c_1 = g_2 + p_2(g_1 + p_1 c_0) = g_2 + p_2 g_1 + p_2 p_1 c_0c2=g2+p2c1=g2+p2(g1+p1c0)=g2+p2g1+p2p1c0
- c3=g3+p3c2=g3+p3g2+p3p2g1+p3p2p1c0c_3 = g_3 + p_3 c_2 = g_3 + p_3 g_2 + p_3 p_2 g_1 + p_3 p_2 p_1 c_0c3=g3+p3c2=g3+p3g2+p3p2g1+p3p2p1c0
- c4=g4+p4g3+p4p3g2+p4p3p2g1+p4p3p2p1c0c_4 = g_4 + p_4 g_3 + p_4 p_3 g_2 + p_4 p_3 p_2 g_1 + p_4 p_3 p_2 p_1 c_0c4=g4+p4g3+p4p3g2+p4p3p2g1+p4p3p2p1c0
惊人发现 :每一个 cic_ici 都可以直接用 初始输入 (a1a_1a1~aia_iai, b1b_1b1~bib_ibi)和 初始进位 c0c_0c0 表达出来!
这意味着:只要我们知道所有 gjg_jgj 和 pjp_jpj(j ≤ i),就可以立即算出 cic_ici,无需等待 ci−1c_{i-1}ci−1。

三、并行进位的核心思想:先行计算,消除等待
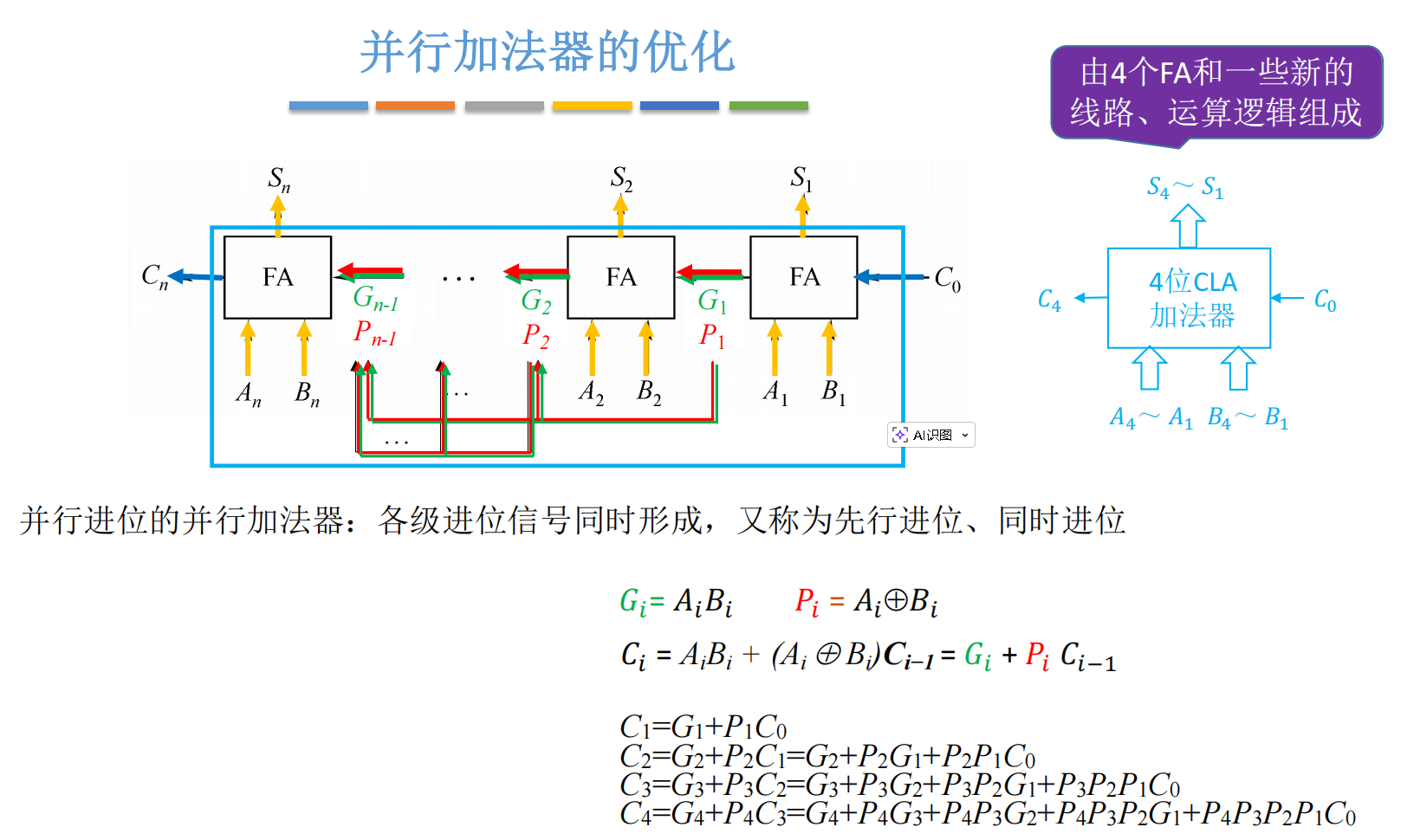
3.1 数据准备阶段:所有原料一开始就齐备
在加法运算开始时,以下信息是已知且稳定的:
- 被加数 A = anan−1...a1a_n a_{n-1} \dots a_1anan−1...a1
- 加数 B = bnbn−1...b1b_n b_{n-1} \dots b_1bnbn−1...b1
- 初始进位 c0c_0c0(通常为 0,除非是带进位加法)
因此,我们可以并行地 计算出所有位的 gig_igi 和 pip_ipi:
- 每一位独立进行 AND 和 XOR 运算;
- 所有 gig_igi、pip_ipi 几乎在同一时刻生成。
3.2 信号广播:G 与 P 的全局共享
关键洞察在于:gjg_jgj 和 pjp_jpj 不仅用于计算 cjc_jcj,还会被所有更高位的进位计算所使用。
例如:
- g1g_1g1 和 p1p_1p1 出现在 c2c_2c2、c3c_3c3、c4c_4c4 的表达式中;
- g2g_2g2 和 p2p_2p2 出现在 c3c_3c3、c4c_4c4 中;
- ......
因此,在硬件设计中,我们需要将每一位生成的 gig_igi、pip_ipi 通过专用布线广播到所有高位的进位逻辑模块中。
3.3 并行生成进位:真正的"同时计算"
以 4 位加法器为例:
- 在 t=0 时刻,输入 A、B、c₀;
- 在 t=Δt 时刻,所有 g1g_1g1$g_4$、$p_1$p4p_4p4 同时生成;
- 在 t=2Δt 时刻,通过组合逻辑电路,c₁、c₂、c₃、c₄ 几乎同时输出!
这与串行进位形成鲜明对比:
- 串行:c₁ → c₂ → c₃ → c₄(4 级延迟)
- 并行:c₁、c₂、c₃、c₄ 同时生成(仅 2~3 级延迟)
这就是"并行进位"或"先行进位"(Carry Lookahead)名称的由来------高位"提前看到"了低位的信息,无需等待。
四、四位 CLA 加法器的硬件实现
4.1 基本组成
一个典型的 4 位 CLA 加法器包含:
- 4 个全加器(FA) :用于计算本位和 si=pi⊕ci−1s_i = p_i \oplus c_{i-1}si=pi⊕ci−1
- G/P 生成模块 :每个位独立计算 gi=aibig_i = a_i b_igi=aibi,pi=ai⊕bip_i = a_i \oplus b_ipi=ai⊕bi
- 先行进位逻辑(Carry Lookahead Logic) :根据 gig_igi、pip_ipi、c0c_0c0 计算 c1c_1c1~c4c_4c4
4.2 进位逻辑电路设计
以 c4c_4c4 为例,其逻辑表达式为:
c4=g4+p4g3+p4p3g2+p4p3p2g1+p4p3p2p1c0 c_4 = g_4 + p_4 g_3 + p_4 p_3 g_2 + p_4 p_3 p_2 g_1 + p_4 p_3 p_2 p_1 c_0 c4=g4+p4g3+p4p3g2+p4p3p2g1+p4p3p2p1c0
该表达式可直接用多级 AND-OR 门实现:
- 第一级:计算所有乘积项(如 p4p3g2p_4 p_3 g_2p4p3g2)
- 第二级:将所有乘积项进行 OR 运算
虽然看起来复杂,但现代 FPGA 或 ASIC 工具可以高效综合此类逻辑。
4.3 性能优势
| 加法器类型 | 进位方式 | 关键路径延迟(以门延迟计) | 适用场景 |
|---|---|---|---|
| 串行进位加法器 | 逐级传递 | O(n) | 小位宽、低成本 |
| 4 位 CLA | 并行生成 | O(1)(常数级) | 高速核心部件 |
对于 4 位运算,CLA 可将延迟从 4 级降至约 2~3 级,提速近 50%。
五、并行进位的局限性
5.1 逻辑复杂度爆炸
虽然 CLA 理论上可以扩展到任意位宽,但表达式长度随位数指数增长:
- c5c_5c5 包含 5 项
- c8c_8c8 包含 8 项
- c16c_{16}c16 包含 16 项......
每一项都是多个信号的 AND,再整体 OR。这导致:
- 电路面积急剧增大;
- 扇入(Fan-in)过高,超出物理门电路的驱动能力;
- 布线复杂,信号延迟反而可能增加。
5.2 实践:分组先行进位(Hierarchical CLA)
为平衡速度与复杂度,实际处理器采用分层设计:
- 底层:使用 4 位或 8 位 CLA 模块;
- 高层:将多个 CLA 模块级联,模块间仍用串行进位,但模块内部并行。
例如,一个 16 位加法器可由 4 个 4 位 CLA 组成:
- 每个 4 位组内部进位并行生成;
- 组与组之间通过"组进位"信号串行传递。
更高级的设计还会引入组生成(Group Generate) 和 组传播(Group Propagate) 信号,实现两级甚至三级先行进位,进一步优化延迟。
5.3 为什么教材只讲到 4 位?
正因上述复杂性,教学中通常以 4 位 CLA 为例,展示先行进位的思想即可。它足够体现核心原理,又不至于让初学者陷入逻辑爆炸的泥潭。
六、总结:从思想到实践的跨越
并行进位加法器的诞生,是数字系统设计中"用空间换时间"的经典范例。它通过增加硬件复杂度(更多逻辑门、更复杂布线),换取了关键路径延迟的大幅降低,从而提升了整体运算速度。
虽然我们在考试中可能只需记住"CLA 比串行快",但理解其背后的数学推导与工程权衡,能帮助我们:
- 更好地理解 CPU 中 ALU 的设计;
- 在 FPGA 开发中合理选择加法器结构;
- 对"延迟 vs 面积"这一永恒矛盾有更深体会。
最后再次提醒:本节内容偏理论,非考试重点 。若一时难以完全掌握,不必焦虑。重要的是抓住核心思想------通过数学展开,将串行依赖转化为并行计算。这种思维方式,在后续学习缓存、流水线、超标量等高性能技术时,依然会反复出现。
延伸思考:
- 如果让你设计一个 8 位 CLA,你会如何划分 G/P 信号?
- 在超大规模集成电路中,如何解决高扇入 OR 门的物理限制?
- 现代 CPU(如 Intel Core 或 ARM Cortex)中的加法器,是否真的使用纯 CLA?还是混合结构?
欢迎在评论区交流你的想法!