一. 前言
在机器学习的核心工作流中,模型评估与选择是确保最终模型泛化能力的关键。当数据有限时,如何准确评估模型性能、避免过拟合成为核心挑战。交叉验证作为一种强大而经典的统计方法,通过最大限度地利用有限数据,为我们提供了对模型性能更稳健、更无偏的估计。它不仅是传统机器学习中模型选择与超参数调优的黄金标准,更以其"重复利用与平均验证"的核心理念,深刻影响了现代机器学习的工作范式。
今天我们将深入浅出地解析交叉验证的思想起源与数学基础,详细剖析k折交叉验证等主流变体的工作机制与实现细节,并系统展示其如何科学地指导模型比较与超参数优化。随着我们进入大模型时代,面对千亿参数与海量数据,交叉验证的传统形式正经历深刻演变。我们将探讨其在大规模预训练、指令微调等新场景下面临的挑战与适应性调整,揭示这一经典方法在现代AI实践中的全新定位与价值延续。从基础原理到前沿应用,构建交叉验证的完整知识体系。

二、什么是交叉验证
当我们开发一个预测模型时,最大的挑战是如何准确判断这个模型在未知数据上的表现。如果仅仅使用单次的数据划分,比如用70%数据训练、30%数据测试,评估结果往往会受到具体划分方式的强烈影响。这种划分可能恰好让模型碰上好运,也可能让模型遭遇不测,从而导致我们对模型性能产生过于乐观或悲观的误判。
交叉验证的精妙之处就在于它采用了一种轮换验证的机制。以最常用的5折交叉验证为例,它将原始数据随机均匀分成5个互斥的子集。在每一轮验证中,其中一个子集扮演验证集的角色,用来测试模型性能,而其余四个子集则共同组成训练集,用于模型构建。这个过程重复进行5次,确保每个数据子集都有机会被用作验证集,最终将5次验证结果进行平均,得到模型的综合性能评分。
这种方法带来了两个关键优势:
- 首先,它极大地降低了评估结果的随机性,使得性能估计更加稳定和可靠。无论数据如何分布,通过这种轮换测试得到的平均成绩都能够更真实地反映模型的泛化能力。
- 其次,它最大限度地利用了有限的数据资源,让几乎所有的样本都既参与了训练又参与了验证,这对于数据稀缺的场景尤其宝贵。
用一个更生活化的例子来通俗的解释交叉验证,如果我们想判断一位家教老师的教学水平如何:
1. 普通的方法,单次测试:
- 假设我们有10套真题,一般我们会让这位老师只用8套真题辅导学生,然后用剩下的2套真题来测试学生成绩。
- 问题:如果测试用的2套题恰好是老师重点讲过的题型,成绩就会虚高;反之,如果全是没讲过的冷门题,成绩就会偏低,这种评估方式非常依赖运气。
2. 交叉验证的方法,轮换测试:
我们可以采用更科学的方式来评估:
- 第一步:准备5套难度相近的测试卷(A、B、C、D、E)。
- 第二步:进行5轮教学测试:
- 第1轮:老师用 B、C、D、E 卷辅导学生,然后用 A卷 测试,记录分数。
- 第2轮:老师用 A、C、D、E 卷辅导学生,然后用 B卷 测试,记录分数。
- 重复这个过程,直到每套试卷都当过一次测试卷。
- 第三步:计算这5个分数的平均值。
这个平均分就能客观、稳定地反映出老师的真实教学水平。
交叉验证体现的价值:
- 评估更公平:不依赖某一次特定的考试运气,结果更具代表性。
- 数据利用更高效:所有试卷都既用于教学又用于测试,物尽其用。
综上所诉,交叉验证就像一套严谨的教师评估体系,通过轮换测试取平均分的方式,确保评估结果的客观性和可靠性,帮助我们做出最佳决策。
三、交叉验证的特点
在理想情况下,我们拥有无限的数据。我们可以将数据分为三部分:
- 训练集:用于构建模型。
- 验证集:用于在训练过程中评估模型,指导模型选择和调参。
- 测试集:用于最终、一次性地评估模型的泛化性能,模拟真实世界应用。
然而,现实是数据通常有限。如果我们简单地使用一个固定的"训练-验证"分割,会引入两个主要问题:
- **1. 评估结果方差高:**模型性能对数据如何分割非常敏感。一次幸运或不幸的分割可能导致我们对模型性能产生过于乐观或悲观的估计。
- **2. 数据利用不充分:**特别是当数据集较小时,留出一部分作为验证集意味着模型无法从这些宝贵的数据中学习,这本身就会导致模型性能下降。
**交叉验证的核心理念:**通过多次、有组织地划分训练集和验证集,让每一份数据都有机会充当训练集和验证集,从而得到多个性能评估值。最终,我们取这些评估值的平均值作为模型性能的最终估计。这种方法显著降低了评估结果的方差,并更充分地利用了数据。
四、k折交叉验证
在众多交叉验证方法中,k折交叉验证 无疑是最常用、最经典的一种。
工作原理:
- **1. 分割:**将原始训练数据集随机、均匀地分割成k个大小相似的互斥子集,称为"折",通常k取5或10。
- **2. 迭代训练与验证:**进行k次迭代。在每一次迭代 i (i=1, 2, ..., k) 中:
- 将第 i 折数据作为验证集。
- 将剩余的 k-1 折数据合并,作为训练集。
- 在训练集上训练模型,并在验证集上评估模型,得到一个性能得分 S_i(如准确率、F1分数等)。
- **3. 性能汇总:**完成k次迭代后,我们会得到k个性能得分 S_1, S_2, ..., S_k。
- **4. 计算最终性能:**将这k个得分取平均值,作为该模型泛化性能的最终估计:
- 最终性能 = (S_1 + S_2 + ... + S_k) / k
- **5. 报告不确定性:**同时,我们还可以计算这k个得分的标准差,以衡量模型性能的稳定性。标准差越小,说明模型对数据分割不敏感,越稳定。
执行过程:
假设 k=5,过程如下所示:
初始数据集: [------------------------------------]
分割为5折: [折1][折2][折3][折4][折5]
迭代1: 训练集:[折2][折3][折4][折5] 验证集:[折1] -> 得分S1
迭代2: 训练集:[折1][折3][折4][折5] 验证集:[折2] -> 得分S2
迭代3: 训练集:[折1][折2][折4][折5] 验证集:[折3] -> 得分S3
迭代4: 训练集:[折1][折2][折3][折5] 验证集:[折4] -> 得分S4
迭代5: 训练集:[折1][折2][折3][折4] 验证集:[折5] -> 得分S5
k值的选择:
- k较小(如k=5):训练成本低,但评估结果的偏差可能略高,因为训练集相对较小。
- k较大(如k=10):评估结果的偏差更低,更接近真实泛化性能,但训练成本是k=5的两倍。
- 留一法交叉验证:k等于样本数N,这是k折交叉验证的极端情况,它能最无偏地估计性能,但计算成本极高,通常只用于极小型数据集。
五、交叉验证在模型选择中的作用
交叉验证本身是一个评估方法,但其威力在模型比较和超参数优化中得以真正体现。
1. 模型选择
假设我们需要在逻辑回归、支持向量机和随机森林中选择一个最佳模型。我们不能直接在测试集上测试并选择最好的,因为这会导致信息泄露,使测试集失去其最终评估的意义。
**正确做法:**对每个候选模型,独立进行一次k折交叉验证,得到各自的平均性能得分,然后选择平均得分最高的模型,这个过程完全在原始训练集内完成,没有动用测试集。
2. 超参数调优
超参数不是从数据中学到的,需要手动设定,寻找最佳超参数组合的过程就是调参,超参数详细内容可参考《六十七、超参数如何影响大模型?通俗讲解原理、作用与实战示例》。
- 网格搜索交叉验证:
- 为每个超参数定义一个候选值列表。
- 这些候选值会组成一个"网格",每个网格点是一组特定的超参数组合。
- 对网格中的每一组超参数组合,执行一次完整的k折交叉验证,计算其平均性能。
- 最终,选择平均性能最高的那组超参数作为最优解。
- 随机搜索交叉验证:
- 与网格搜索不同,它不在一个定义好的网格上搜索,而是从一个指定的概率分布中随机采样一定数量的超参数组合。
- 对每个随机采样的组合执行k折交叉验证。
- 实践证明,随机搜索通常比网格搜索更高效,能以更少的尝试次数找到优秀的超参数。
通过交叉验证选出的最佳模型或最佳参数,其性能是那个平均性能。在完成所有模型选择和调参后,我们通常会用这组最佳参数在整个原始训练集上重新训练一个最终模型,然后用从未参与过任何过程的测试集来报告其最终的、无偏的性能。
六、 使用交叉验证评估分类模型
下面我们演示一个基础示例,使用Scikit-learn库实现k折交叉验证。用交叉验证科学地判断一个模型的好坏,并把它调整到最佳状态。
1. 执行流程
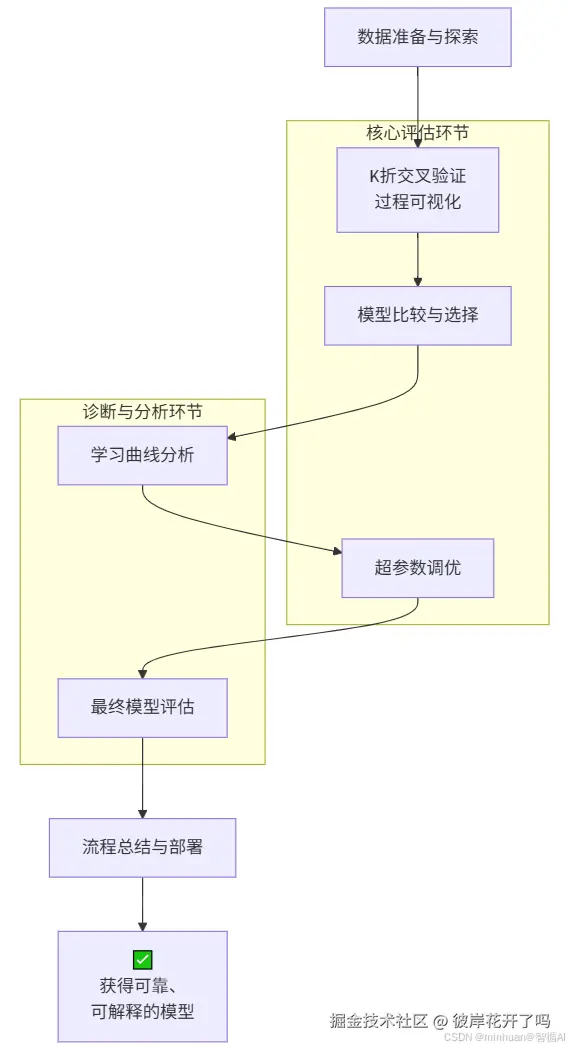
2. 流程概述
- 核心评估环节
- K折交叉验证:通过数据轮换使用,获得稳健的性能评估
- 模型比较与选择:基于交叉验证结果客观选择最佳模型
- 超参数调优:使用交叉验证寻找最优参数组合
- 诊断与分析环节
- 学习曲线分析:诊断模型是否过拟合或欠拟合
- 最终模型评估:在独立测试集上全面检验模型表现
3. 示例分解
3.1 准备环境和数据可视化
示例采用的是scikit-learn库的鸢尾花数据集,数据集包含150个样本,每个样本有4个特征和1个标签,在前期我们讲决策树时我们专门讲解过,这里简单概述一下,需要深入了解请参考《三十五、决策树的核心机制(一):刨根问底鸢尾花分类中的参数推理计算》。
数据集合包含三种鸢尾花:
- **Iris Setosa:**山鸢尾,最容易识别,花瓣短而宽,花萼较大。
- **Iris Versicolor:**变色鸢尾,介于另外两种之间,颜色多变。
- **Iris Virginica:**维吉尼亚鸢尾,最大最壮观,花瓣和花萼尺寸都最大。
4个特征(预测依据):
- sepal length (cm) - 花萼长度
- sepal width (cm) - 花萼宽度
- petal length (cm) - 花瓣长度
- petal width (cm) - 花瓣宽度
1个标签(预测目标):
- species - 品种(0: Setosa, 1: Versicolor, 2: Virginica)
数据集的构成:
整个数据集就是一个大表格,有150行(代表150朵不同的花)和5列。
品种 (标签) 花萼长度 花萼宽度 花瓣长度 花瓣宽度
Iris-setosa 5.1 3.5 1.4 0.2
Iris-versicolor 7.0 3.2 4.7 1.4
Iris-virginica 6.3 3.3 6.0 2.5
python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score, KFold, train_test_split, GridSearchCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.metrics import classification_report, confusion_matrix
import warnings
warnings.filterwarnings('ignore')
# 设置中文字体和图形样式
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
sns.set_style("whitegrid")
# 加载数据
iris = load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
target_names = iris.target_names
print("数据集探索")
print(f"数据集形状: {X.shape}")
print(f"特征: {feature_names}")
print(f"类别: {target_names}")输出结果:
数据集探索
数据集形状: (150, 4)
特征: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
类别: ['setosa' 'versicolor' 'virginica']
3.2 数据分布可视化
在建模之前,先了解我们要处理的数据,通过绘制特征的分布直方图,判断数据质量、特征区分度以及不同类别的分离情况,为后续的模型选择提供初步依据。
scss
# 创建数据分布可视化
def plot_data_distribution(X, y, feature_names, target_names):
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
axes = axes.ravel()
# 特征分布
for i in range(4):
for class_id in range(3):
axes[i].hist(X[y == class_id, i], alpha=0.7, label=target_names[class_id])
axes[i].set_title(f'{feature_names[i]} 分布')
axes[i].set_xlabel('值')
axes[i].set_ylabel('频数')
axes[i].legend()
plt.tight_layout()
plt.show()
plot_data_distribution(X, y, feature_names, target_names)输出结果:
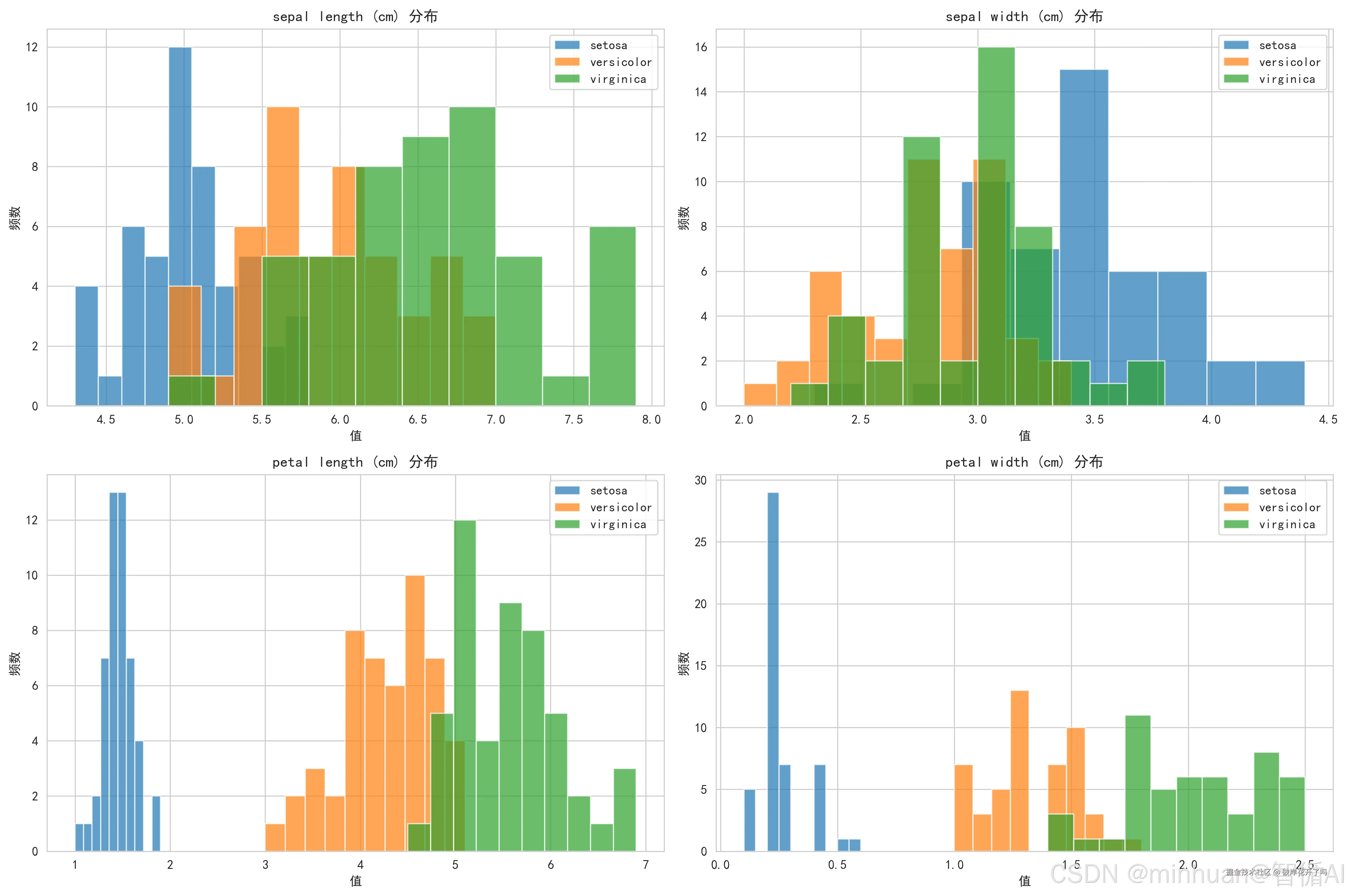
图示内容:
- 显示4个特征(花萼长度、花萼宽度、花瓣长度、花瓣宽度)在3个类别间的分布直方图
- 每个子图展示一个特征,不同类别用不同颜色区分
3.3 k折交叉验证过程可视化
直观演示交叉验证的核心原理,通过图表清晰地展示每一折中,哪些样本用于训练(蓝色),哪些用于验证(红色),并实时显示该折的验证得分,最后使用柱状图汇总对比各折的准确率,使结果一目了然,这可以让我们彻底理解轮"换考试"和"平均分"的概念。
ini
def visualize_kfold_process(X, y, k=5):
"""可视化k折交叉验证的数据分割过程"""
kf = KFold(n_splits=k, shuffle=True, random_state=42)
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
axes = axes.ravel()
fold_scores = []
for fold, (train_idx, val_idx) in enumerate(kf.split(X)):
if fold < 6: # 只显示前6个图
ax = axes[fold]
# 创建分割可视化
split_diagram = np.zeros(len(X))
split_diagram[train_idx] = 1 # 训练集
split_diagram[val_idx] = 2 # 验证集
# 绘制分割图
colors = ['lightgray', 'blue', 'red']
labels = ['未使用', '训练集', '验证集']
for i, color in enumerate(colors):
ax.bar(range(len(split_diagram)),
[1 if x == i else 0 for x in split_diagram],
color=color, label=labels[i])
ax.set_title(f'第 {fold+1} 折数据分割\n训练集: {len(train_idx)}样本, 验证集: {len(val_idx)}样本')
ax.set_xlabel('样本索引')
ax.set_ylabel('数据用途')
ax.legend()
# 训练模型并计算分数
model = RandomForestClassifier(random_state=42)
model.fit(X[train_idx], y[train_idx])
score = model.score(X[val_idx], y[val_idx])
fold_scores.append(score)
# 在图中添加准确率
ax.text(0.5, 0.9, f'准确率: {score:.3f}',
transform=ax.transAxes, ha='center',
bbox=dict(boxstyle="round,pad=0.3", facecolor="yellow", alpha=0.7))
# 在右下角子图绘制各折准确率条形图,并隐藏其他多余子图
summary_ax_index = len(axes) - 1 # 右下角子图索引(2x3 网格中的最后一个)
for i in range(len(axes)):
if i >= k and i != summary_ax_index:
axes[i].set_visible(False)
# 绘制各折准确率条形图
ax_summary = axes[summary_ax_index]
ax_summary.set_visible(True)
bars = ax_summary.bar([f'折{i+1}' for i in range(len(fold_scores))], fold_scores, color='teal', alpha=0.8)
ax_summary.set_title('各折准确率')
ax_summary.set_ylabel('准确率')
ax_summary.set_ylim(0, 1.05)
for bar, score in zip(bars, fold_scores):
height = bar.get_height()
ax_summary.text(bar.get_x() + bar.get_width()/2., height + 0.02, f'{score:.3f}', ha='center', va='bottom')
plt.tight_layout()
plt.show()
return fold_scores
print(" k折交叉验证过程可视化")
fold_scores = visualize_kfold_process(X, y, k=5)输出结果:
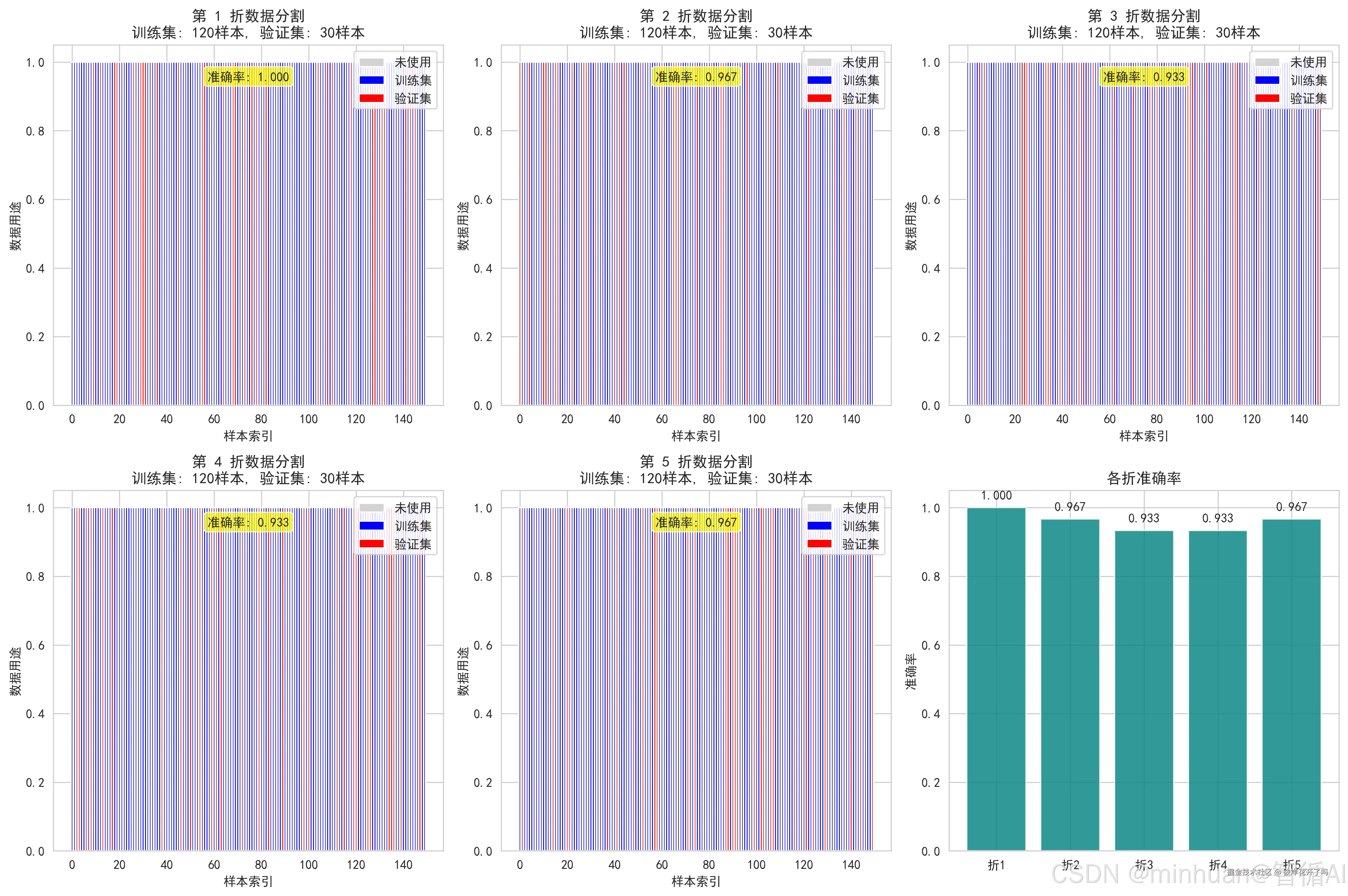
图示内容:
- 展示5折交叉验证中每折的数据分割情况
- 训练集(蓝色)、验证集(红色)的样本分配
- 每折的验证准确率显示
- 各折的准确率综合对比显示
k折交叉验证公式:
设数据集 D = {(x₁,y₁), (x₂,y₂), ..., (x_N,y_N)}
将 D 分割为 k 个互斥子集:D₁, D₂, ..., D_k
对于每个折 i = 1, 2, ..., k:
训练集:D_train⁽ⁱ⁾ = D \ D_i
验证集:D_val⁽ⁱ⁾ = D_i
模型训练:f⁽ⁱ⁾ = train(D_train⁽ⁱ⁾)
性能评估:score⁽ⁱ⁾ = evaluate(f⁽ⁱ⁾, D_val⁽ⁱ⁾)
最终性能:CV_score = (1/k) * Σ_{i=1}^k score⁽ⁱ⁾
性能标准差:CV_std = √[ (1/(k-1)) * Σ_{i=1}^k (score⁽ⁱ⁾ - CV_score)² ]
体现的价值:
- 数据利用最大化:每个样本都参与训练和验证
- 性能估计无偏性:减少单次分割的随机性影响
- 模型稳定性评估:通过标准差衡量模型鲁棒性
3.4 模型比较可视化
科学地回答"哪个模型更好?",通过柱状图(带误差棒)和箱线图,同时比较多个模型(如随机森林、逻辑回归、SVM)的平均性能和稳定性,这不仅看谁的平均分高,还要看谁的表现更稳定(方差小),从而做出稳健的选择。
ini
def compare_models_cv(X, y, models, cv=5):
"""比较不同模型的交叉验证性能并可视化"""
model_names = []
mean_scores = []
std_scores = []
all_scores = []
print(" 模型性能比较")
for name, model in models.items():
# 执行交叉验证
cv_scores = cross_val_score(model, X, y, cv=cv, scoring='accuracy')
model_names.append(name)
mean_scores.append(cv_scores.mean())
std_scores.append(cv_scores.std())
all_scores.append(cv_scores)
print(f"{name:15} | 平均准确率: {cv_scores.mean():.4f} (±{cv_scores.std():.4f})")
# 创建性能比较图
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# 柱状图比较平均性能
bars = ax1.bar(model_names, mean_scores, yerr=std_scores,
capsize=5, alpha=0.7, color=['skyblue', 'lightgreen', 'lightcoral'])
ax1.set_title('模型交叉验证性能比较')
ax1.set_ylabel('平均准确率')
ax1.set_ylim(0.8, 1.0)
# 在柱子上添加数值
for bar, score in zip(bars, mean_scores):
height = bar.get_height()
ax1.text(bar.get_x() + bar.get_width()/2., height + 0.01,
f'{score:.4f}', ha='center', va='bottom')
# 箱线图显示分布
ax2.boxplot(all_scores, labels=model_names)
ax2.set_title('各折准确率分布')
ax2.set_ylabel('准确率')
plt.tight_layout()
plt.show()
# 选择最佳模型
best_idx = np.argmax(mean_scores)
best_model_name = model_names[best_idx]
best_model = models[best_model_name]
print(f"\n 最佳模型: {best_model_name} (准确率: {mean_scores[best_idx]:.4f})")
return best_model_name, best_model, all_scores
# 定义要比较的模型
models = {
'随机森林': RandomForestClassifier(random_state=42),
'逻辑回归': LogisticRegression(random_state=42, max_iter=1000),
'支持向量机': SVC(random_state=42)
}
best_model_name, best_model, all_scores = compare_models_cv(X, y, models)输出结果:
模型性能比较
随机森林 | 平均准确率: 0.9667 (±0.0211)
逻辑回归 | 平均准确率: 0.9733 (±0.0249)
支持向量机 | 平均准确率: 0.9667 (±0.0211)
最佳模型: 逻辑回归 (准确率: 0.9733)
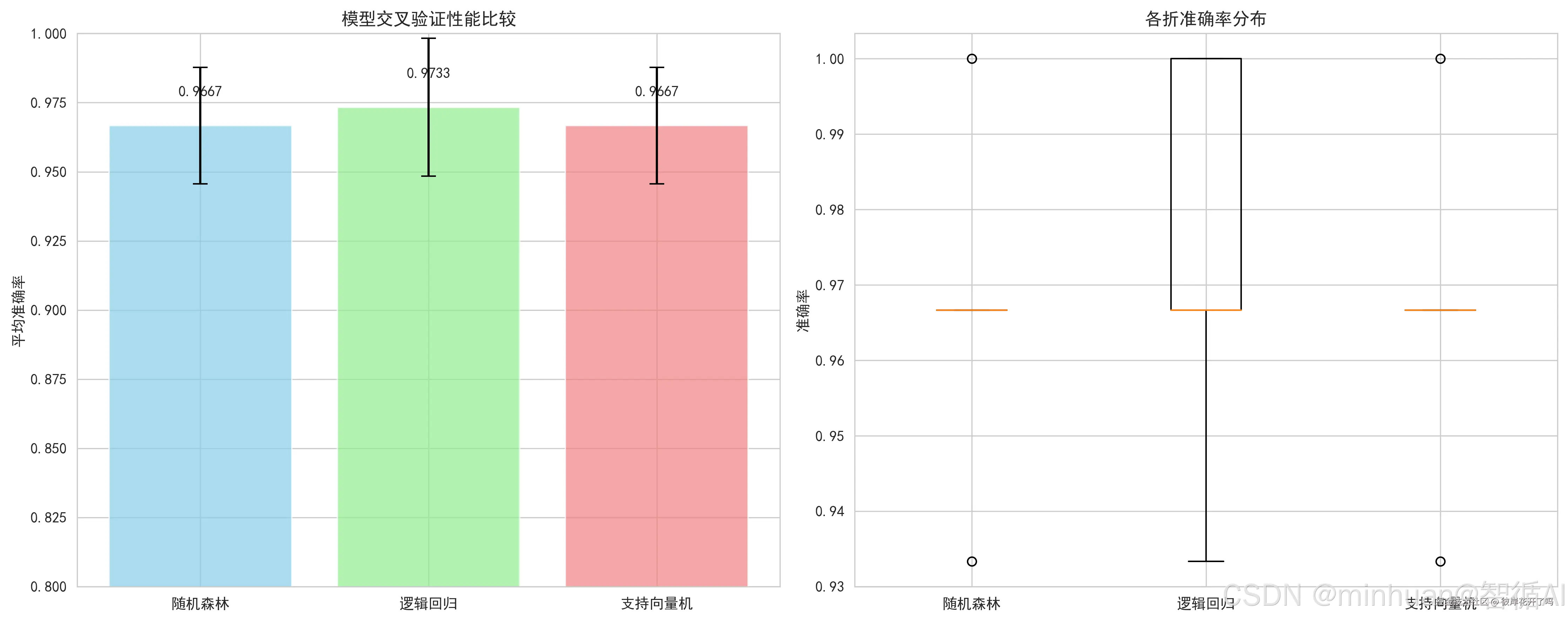
图示内容:
- 左侧柱状图:各模型平均准确率及误差棒(标准差)
- 右侧箱线图:各模型5折交叉验证得分的分布
模型性能比较的统计检验:
设两个模型 A 和 B 的k折得分分别为:
scores_A = [s_A¹, s_A², ..., s_Aᵏ]
scores_B = [s_B¹, s_B², ..., s_Bᵏ]
配对t检验统计量:
t = (mean(scores_A) - mean(scores_B)) / √[ (var(scores_A - scores_B) / k) ]
其中:
var(scores_A - scores_B) = (1/(k-1)) * Σ_{i=1}^k [(s_Aⁱ - s_Bⁱ) - mean(scores_A - scores_B)]²
体现的价值:
- 模型选择依据:基于统计性能选择最佳模型
- 性能稳定性分析:通过分布了解模型鲁棒性
- 统计显著性判断:确定性能差异是否显著
3.5 学习曲线可视化
诊断模型状态的关键工具,通过绘制模型随训练数据量增加时,训练得分和验证得分的变化曲线,可以清晰地判断模型是处于过拟合(训练得分远高于验证得分)还是欠拟合(两者都低)状态,并指导是否需要收集更多数据。
scss
def plot_learning_curve(model, X, y, model_name):
"""绘制学习曲线来观察模型表现"""
from sklearn.model_selection import learning_curve
train_sizes, train_scores, test_scores = learning_curve(
model, X, y, cv=5, n_jobs=-1,
train_sizes=np.linspace(0.1, 1.0, 10),
scoring='accuracy'
)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.figure(figsize=(10, 6))
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1, color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color="r", label="训练得分")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g", label="交叉验证得分")
plt.title(f'{model_name} 学习曲线')
plt.xlabel('训练样本数')
plt.ylabel('准确率')
plt.legend(loc="best")
plt.grid(True)
plt.show()
print("\n 学习曲线分析")
for name, model in models.items():
plot_learning_curve(model, X, y, name)输出结果:
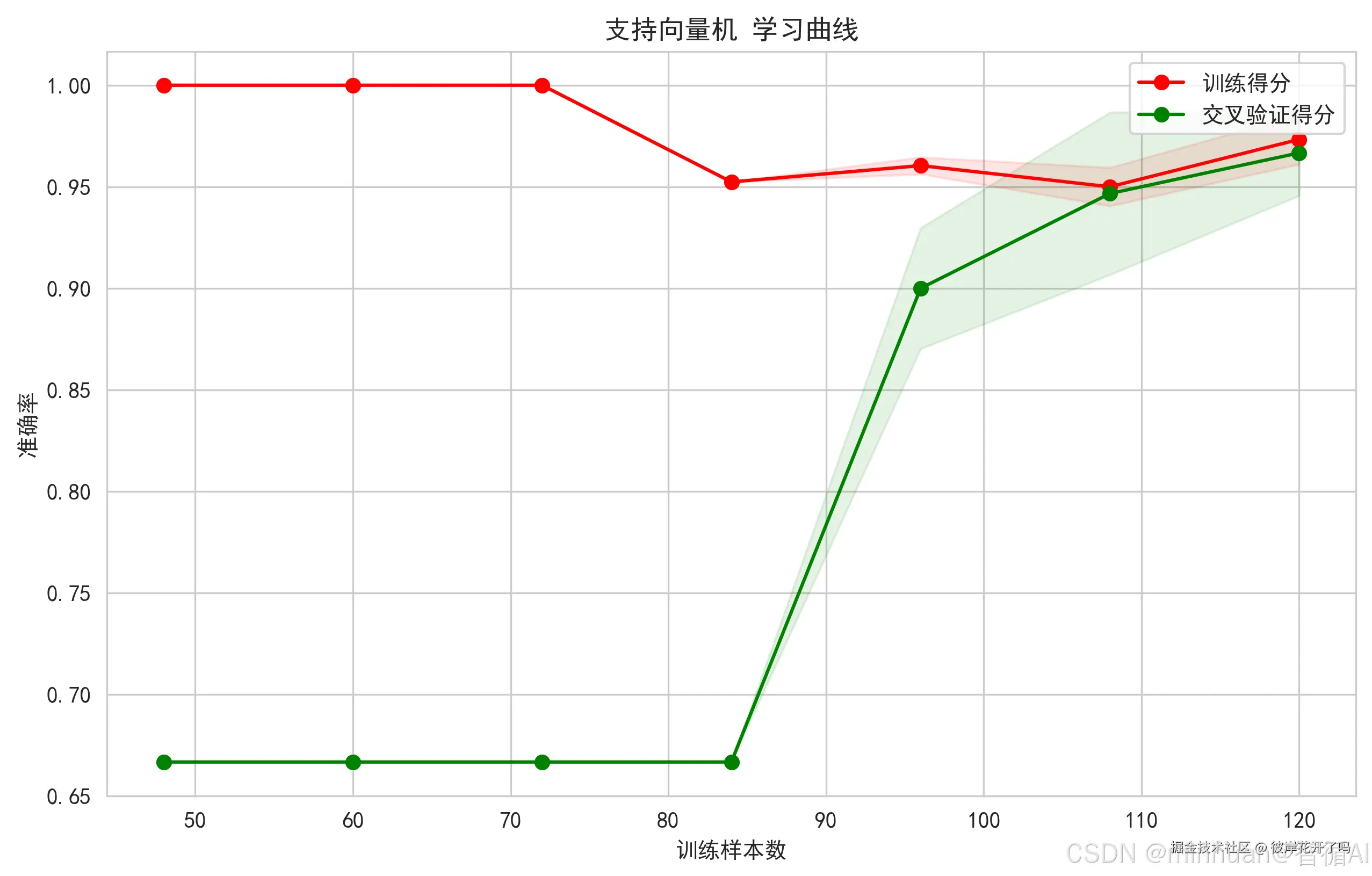
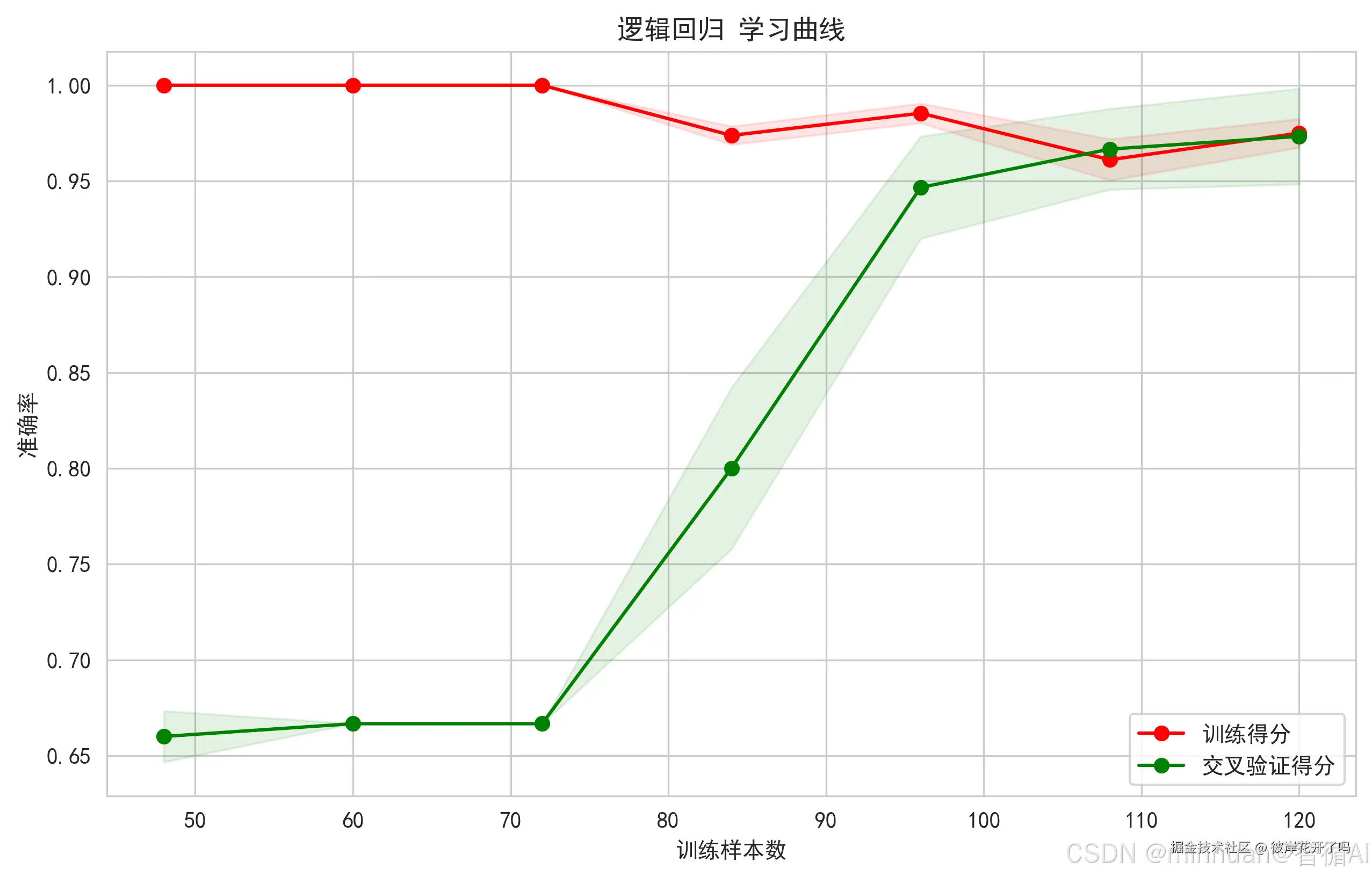
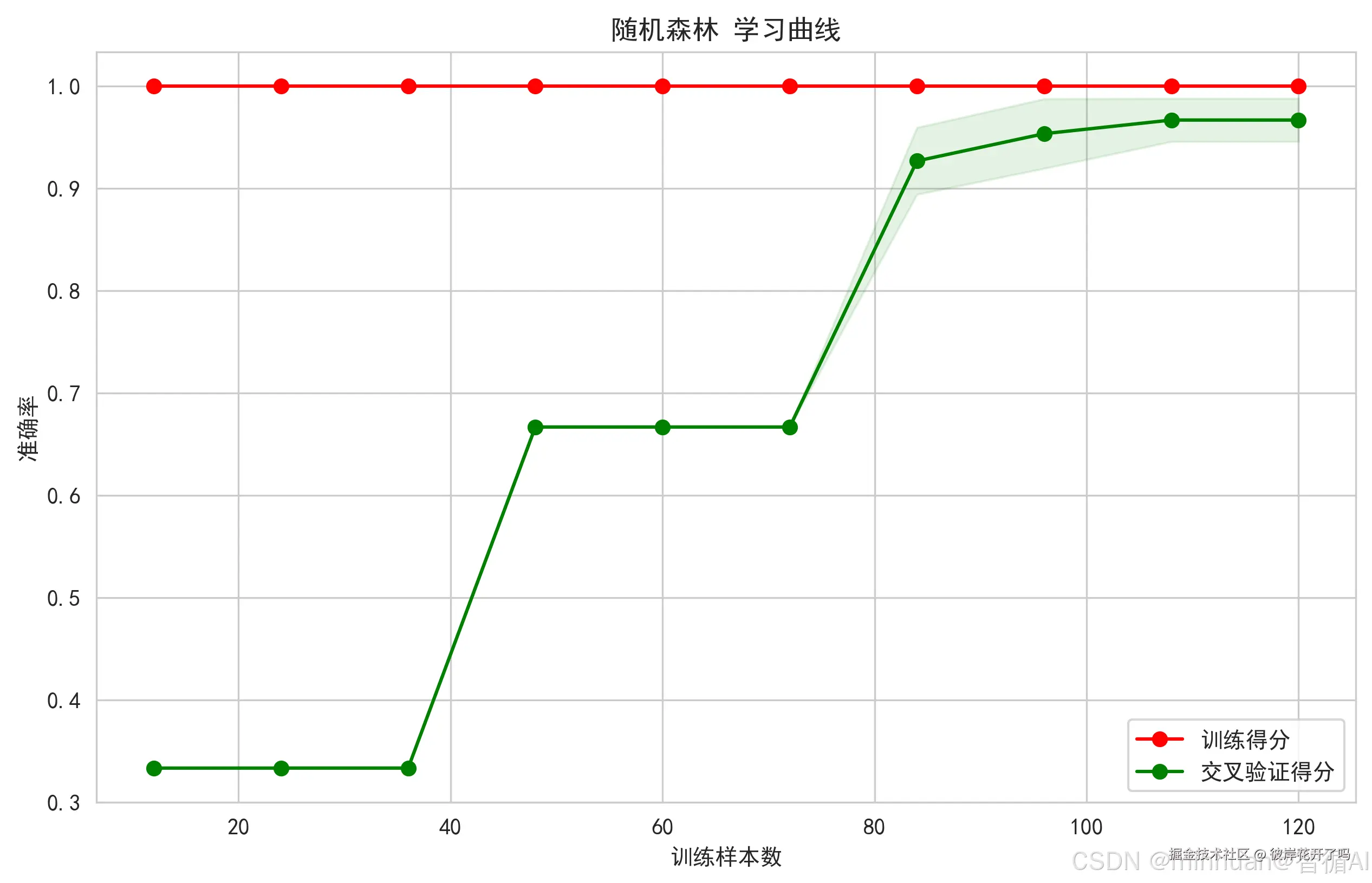
图示内容:
- 训练得分和验证得分随训练样本数量增加的变化
- 阴影区域表示得分的标准差范围
学习曲线理论:
设训练集大小为 m,模型复杂度为 h
训练误差:J_train(m) = (1/m) * Σ_{i=1}^m L(f(x_i), y_i)
验证误差:J_val(m) = (1/k) * Σ_{j=1}^k L(f(x_j), y_j)
随着 m → ∞:
J_train(m) → 模型偏差 + 方差项
J_val(m) → 模型偏差 + 方差项 + 噪声项
其中偏差-方差分解:
E[(y - f(x))²] = Bias[f(x)]² + Var[f(x)] + σ²
体现的价值:
- 过拟合/欠拟合诊断:判断模型是否合适
- 数据量需求评估:确定需要多少训练数据
- 模型容量分析:观察模型的学习能力
3.6 网格搜索调参可视化
科学的调参方式,通过网格搜索交叉验证,系统性地遍历不同的参数组合,并用热力图等形式展示参数如何影响性能。这帮助我们找到真正的最佳参数组合,并理解参数之间的相互作用。
python
def visualize_grid_search(X, y):
"""可视化网格搜索过程"""
# 定义参数网格
param_grid = {
'n_estimators': [50, 100, 200],
'max_depth': [3, 5, None],
'min_samples_split': [2, 5, 10]
}
rf = RandomForestClassifier(random_state=42)
grid_search = GridSearchCV(rf, param_grid, cv=5, scoring='accuracy', n_jobs=-1)
grid_search.fit(X, y)
# 可视化结果
results = pd.DataFrame(grid_search.cv_results_)
# 选择部分参数进行可视化
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# 1. n_estimators 的影响
param1_data = results[results['param_max_depth'].isna() & results['param_min_samples_split'] == 2]
axes[0,0].plot(param1_data['param_n_estimators'], param1_data['mean_test_score'], 'o-')
axes[0,0].set_title('n_estimators 对性能的影响\n(max_depth=None, min_samples_split=2)')
axes[0,0].set_xlabel('n_estimators')
axes[0,0].set_ylabel('平均准确率')
# 2. max_depth 的影响
param2_data = results[results['param_n_estimators'] == 100 & results['param_min_samples_split'] == 2]
axes[0,1].plot([str(x) for x in param2_data['param_max_depth']], param2_data['mean_test_score'], 'o-')
axes[0,1].set_title('max_depth 对性能的影响\n(n_estimators=100, min_samples_split=2)')
axes[0,1].set_xlabel('max_depth')
axes[0,1].set_ylabel('平均准确率')
# 3. 热力图:n_estimators vs max_depth
heatmap_data = results.pivot_table(
values='mean_test_score',
index='param_n_estimators',
columns='param_max_depth',
aggfunc='mean'
)
sns.heatmap(heatmap_data, annot=True, fmt='.3f', cmap='YlOrRd', ax=axes[1,0])
axes[1,0].set_title('参数组合热力图\n(平均准确率)')
# 4. 最佳参数组合
best_params = grid_search.best_params_
best_score = grid_search.best_score_
axes[1,1].text(0.1, 0.8, f'最佳参数组合:', fontsize=14, weight='bold')
axes[1,1].text(0.1, 0.6, f'n_estimators: {best_params["n_estimators"]}', fontsize=12)
axes[1,1].text(0.1, 0.5, f'max_depth: {best_params["max_depth"]}', fontsize=12)
axes[1,1].text(0.1, 0.4, f'min_samples_split: {best_params["min_samples_split"]}', fontsize=12)
axes[1,1].text(0.1, 0.2, f'最佳准确率: {best_score:.4f}', fontsize=14, weight='bold', color='red')
axes[1,1].set_xlim(0, 1)
axes[1,1].set_ylim(0, 1)
axes[1,1].set_title('最佳参数结果', fontsize=14)
axes[1,1].axis('off')
plt.tight_layout()
plt.show()
print(f"\n 网格搜索最佳参数: {grid_search.best_params_}")
print(f"最佳交叉验证得分: {grid_search.best_score_:.4f}")
return grid_search.best_estimator_
print("\n 网格搜索调参可视化")
best_tuned_model = visualize_grid_search(X, y)输出结果:
网格搜索调参可视化
网格搜索最佳参数: {'max_depth': 3, 'min_samples_split': 2, 'n_estimators': 50}
最佳交叉验证得分: 0.9667

图示内容:
- 不同超参数组合对模型性能的影响
- 参数热力图显示最佳组合
- 最佳参数结果总结
超参数优化目标:
设超参数空间为 Θ,性能度量函数为 P
网格搜索目标:找到 θ* ∈ Θ 使得
θ* = argmax_{θ∈Θ} CV_score(θ)
其中:
CV_score(θ) = (1/k) * Σ_{i=1}^k P(f_θ⁽ⁱ⁾, D_val⁽ⁱ⁾)
f_θ⁽ⁱ⁾ 是在超参数 θ 下,在第 i 折训练集上训练的模型
体现的价值:
- 超参数敏感性分析:了解各参数对性能的影响
- 最优配置确定:找到最佳超参数组合
- 参数交互作用:观察参数间的相互影响
3.7 最终模型评估可视化
对最佳模型进行全面的毕业答辩,在独立的测试集上,通过混淆矩阵、特征重要性、分类报告等多种工具,从各个角度评估模型的最终表现,了解其错误类型和决策依据,确保其泛化能力。
ini
def final_evaluation_visualization(model, X, y, model_name):
"""最终模型评估可视化"""
# 分割数据
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42, stratify=y
)
# 训练最终模型
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
# 创建评估图表
fig, axes = plt.subplots(2, 2, figsize=(15, 12))
# 1. 混淆矩阵
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues',
xticklabels=target_names, yticklabels=target_names, ax=axes[0,0])
axes[0,0].set_title('混淆矩阵')
axes[0,0].set_xlabel('预测标签')
axes[0,0].set_ylabel('真实标签')
# 2. 特征重要性(如果是树模型)
if hasattr(model, 'feature_importances_'):
importances = model.feature_importances_
indices = np.argsort(importances)[::-1]
axes[0,1].bar(range(len(importances)), importances[indices])
axes[0,1].set_title('特征重要性')
axes[0,1].set_xlabel('特征')
axes[0,1].set_ylabel('重要性')
axes[0,1].set_xticks(range(len(importances)))
axes[0,1].set_xticklabels([feature_names[i] for i in indices], rotation=45)
# 3. 测试集性能
test_score = model.score(X_test, y_test)
train_score = model.score(X_train, y_train)
scores = [train_score, test_score]
labels = ['训练集', '测试集']
bars = axes[1,0].bar(labels, scores, color=['lightblue', 'lightcoral'])
axes[1,0].set_title('训练集 vs 测试集 性能')
axes[1,0].set_ylabel('准确率')
axes[1,0].set_ylim(0, 1.1)
# 在柱子上添加数值
for bar, score in zip(bars, scores):
height = bar.get_height()
axes[1,0].text(bar.get_x() + bar.get_width()/2., height + 0.02,
f'{score:.4f}', ha='center', va='bottom')
# 4. 分类报告摘要
report = classification_report(y_test, y_pred, target_names=target_names, output_dict=True)
report_df = pd.DataFrame(report).transpose()
# 简化显示主要指标
axes[1,1].axis('off')
axes[1,1].text(0.1, 0.9, '分类报告摘要', fontsize=16, weight='bold')
y_pos = 0.7
for class_name in target_names:
prec = report[class_name]['precision']
rec = report[class_name]['recall']
f1 = report[class_name]['f1-score']
axes[1,1].text(0.1, y_pos, f'{class_name}:', fontsize=12, weight='bold')
axes[1,1].text(0.4, y_pos, f'精确率: {prec:.3f}, 召回率: {rec:.3f}, F1: {f1:.3f}', fontsize=10)
y_pos -= 0.1
axes[1,1].text(0.1, y_pos-0.1, f'总体准确率: {test_score:.4f}',
fontsize=14, weight='bold', color='red')
plt.tight_layout()
plt.show()
print(f"\n 最终模型评估完成!")
print(f"测试集准确率: {test_score:.4f}")
return test_score
print("\n 最终模型评估可视化")
final_score = final_evaluation_visualization(best_tuned_model, X, y, best_model_name)输出结果:
最终模型评估可视化
最终模型评估完成!
测试集准确率: 0.9667
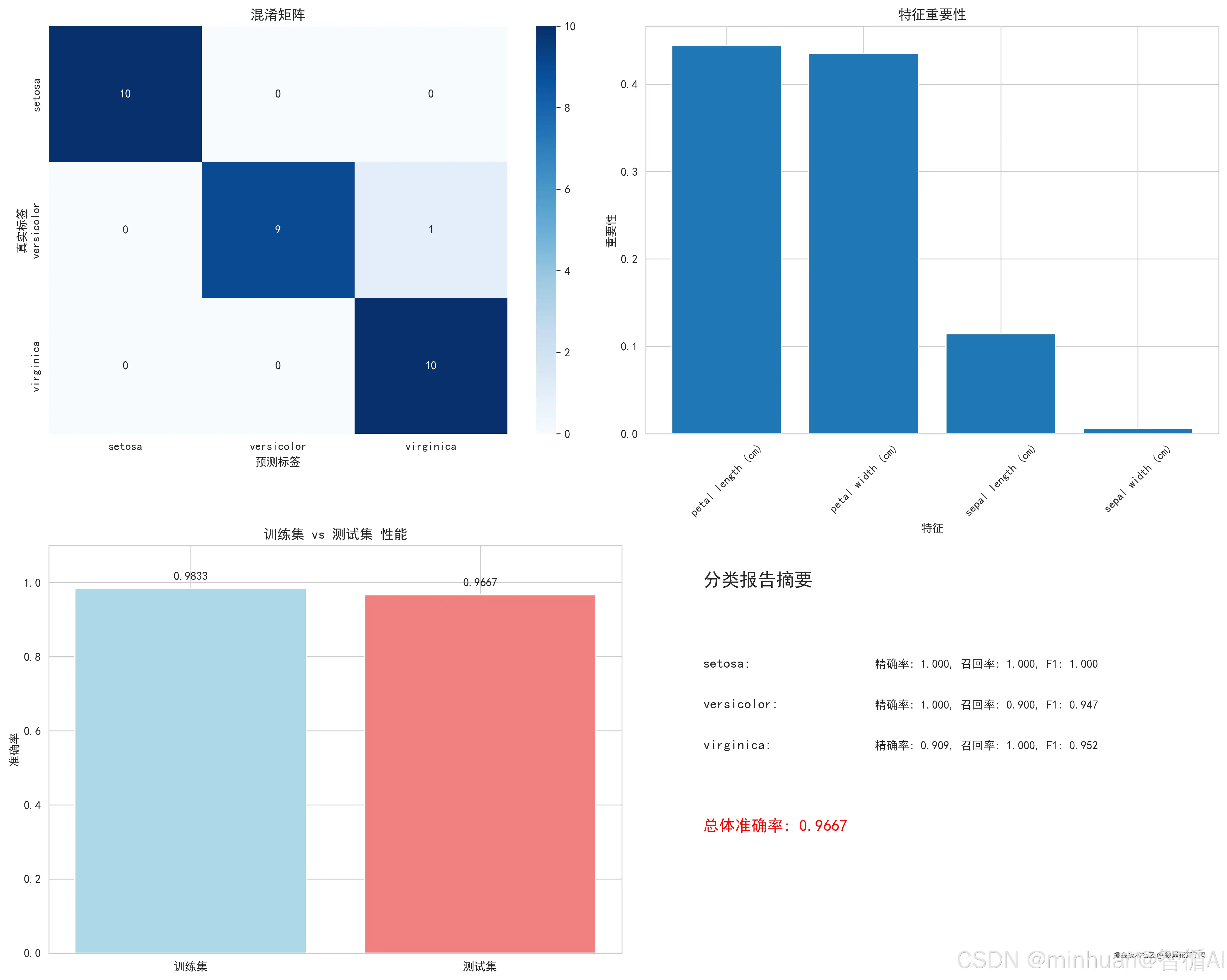
图示内容:
- 混淆矩阵:真实vs预测类别分布
- 特征重要性:各特征对预测的贡献度
- 训练vs测试性能比较
- 详细分类报告
模型评估指标:
对于多分类问题,每个类别 k 的指标:
精确率:Precision_k = TP_k / (TP_k + FP_k)
召回率:Recall_k = TP_k / (TP_k + FN_k)
F1分数:F1_k = 2 * (Precision_k * Recall_k) / (Precision_k + Recall_k)
准确率:Accuracy = (Σ_k TP_k) / N
其中:
TP_k = 真阳性(类别k被正确预测)
FP_k = 假阳性(其他类别被预测为k)
FN_k = 假阴性(类别k被预测为其他)
体现的价值:
- 全面性能评估:多角度评估模型表现
- 错误模式分析:通过混淆矩阵识别常见错误
- 特征贡献度:理解模型决策依据
- 泛化能力验证:比较训练和测试性能
3.8 完整流程总结图
梳理全局,形成方法论,通过一张总结图,将整个流程串联起来,强调每一步的目的和衔接,让我们建立起一个完整、规范的机器学习项目开发观念。
ini
def create_workflow_summary():
"""创建完整的工作流程总结图"""
fig, ax = plt.subplots(figsize=(12, 8))
# 定义流程步骤
steps = [
("1. 数据准备", "加载和探索数据\n数据可视化"),
("2. 交叉验证", "k折数据分割\n模型性能评估"),
("3. 模型比较", "多个模型对比\n选择最佳模型"),
("4. 超参数调优", "网格搜索\n寻找最优参数"),
("5. 最终评估", "测试集验证\n性能可视化"),
("6. 模型部署", "训练最终模型\n投入实际使用")
]
# 绘制流程图
y_positions = [7, 6, 5, 4, 3, 2]
for i, (title, description) in enumerate(steps):
# 绘制方框
box = plt.Rectangle((0.1, y_positions[i]), 0.8, 0.8,
fill=True, color='lightblue', alpha=0.7,
edgecolor='black', linewidth=2)
ax.add_patch(box)
# 添加文本
ax.text(0.5, y_positions[i] + 0.5, title,
ha='center', va='center', fontsize=14, weight='bold')
ax.text(0.5, y_positions[i] + 0.3, description,
ha='center', va='center', fontsize=10)
# 绘制连接箭头
if i < len(steps) - 1:
ax.arrow(0.5, y_positions[i] + 0.1, 0, -0.3,
head_width=0.03, head_length=0.1, fc='black', ec='black')
ax.set_xlim(0, 1)
ax.set_ylim(1, 8)
ax.set_title('机器学习模型开发完整工作流程', fontsize=16, weight='bold', pad=20)
ax.axis('off')
# 添加交叉验证重点说明
ax.text(0.5, 0.8, ' 交叉验证是整个流程的核心环节!',
ha='center', va='center', fontsize=12, weight='bold',
bbox=dict(boxstyle="round,pad=0.3", facecolor="yellow", alpha=0.7))
plt.tight_layout()
plt.show()
print("\n 完整工作流程总结")
create_workflow_summary()输出结果:

完整工作流的数学框架:
完整流程可形式化为:
数据准备:D = {(x_i, y_i)} ∼ P_data
模型选择:M = {m₁, m₂, ..., m_p}
交叉验证:m* = argmax_{m∈M} CV_score(m)
超参数调优:θ* = argmax_{θ} CV_score(m*_θ)
最终评估:Performance = P(m*_θ*, D_test)
部署:f_final = train(m*_θ*, D_all)
这些可视化图表共同构成了一个完整的模型评估和选择框架,每个图表都基于严格的数学原理,提供了从数据理解到模型部署的全方位理解。
七、大模型时代的突破与演进
随着以大语言模型为代表的、参数巨量、训练成本极高的模型出现,经典的k折交叉验证实践面临着严峻挑战:
- **计算成本无法承受:**训练一个大规模的模型需要数月时间和数百万美元的计算资源。进行k次(比如10次)这样的训练来进行交叉验证,在经济和时间上都是不现实的。
- **数据规模巨大:**大模型的训练数据集往往达到TB甚至PB级别。在这种情况下,简单的留出法(例如98%训练,1%验证,1%测试)已经能提供非常稳定和低方差的性能估计。k折交叉验证带来的方差降低收益,与其巨大的计算成本相比,性价比极低。
- **动态训练过程:**大模型的训练不是一次性的,而是涉及复杂的多阶段指令微调、人类反馈强化学习等。验证集在其中扮演着动态监控的角色,用于在单个训练周期内早停、选择检查点等,而非用于多次重新训练。
演进与应对策略:
- **大规模留出法成为主流:**对于预训练和基础模型开发,单一、大规模、高质量的留出验证集是事实上的标准,其规模足以保证评估的稳定性。
- **交叉验证的降级应用:**交叉验证并未完全消失,而是转移到了大模型工作流的下游任务中。
- 提示工程:当为特定任务设计提示时,研究人员可能会在一个较小的示例数据集上使用k折交叉验证来比较不同提示模板的稳定性。
- 超参数微调:在对大模型进行轻量级微调时,学习率、LoRA秩等超参数仍然需要调整。此时,可以在微调数据集上使用交叉验证来寻找最优设置。
- 小样本/少样本学习:在数据极其稀缺的场景下,交叉验证仍然是评估小样本学习策略有效性的重要工具。
- **从"重训练"到"重评估":**理念从"通过多次训练来评估"转向"通过一次训练、在多个维度/数据集上深入评估"。大模型的评估重点不再是单一的准确率,而是涵盖了真实性、毒性、偏见、推理能力、指令遵循能力等更广泛的维度,这需要构建庞大且多样化的评估基准。
扩展说明:
- **大规模留出法:**就像一所拥有数万学生的大学。学校要评估一位教授的教学水平,不需要让所有学生都参加考试。他们只需要随机抽取一个几百人的大班进行统一考试,因为这个班的成绩已经足以稳定、可靠地反映出教授的普遍教学效果。这种方法高效且成本可控。
八、总结
交叉验证作为机器学习模型评估的经典方法,其数学理论基础坚实,实践应用价值显著。它为我们在数据有限的常态下,进行可靠的模型评估、选择和调参提供了坚实的基础。通过系统的可视化分析,我们展示了交叉验证在数据理解、模型比较、超参数优化和最终评估等各个环节的核心作用。
进入大模型时代,虽然其应用场景因计算瓶颈而收缩,但其思想精髓已内化为机器学习工作流的基本逻辑。在资源允许的传统机器学习任务和中下游微调中,它依然是不可或缺的黄金标准;而在大规模基础模型研发中,我们则采用了更符合其经济性的评估范式。理解交叉验证的原理与局限,并能根据具体场景(数据规模、模型复杂度、计算预算)灵活选择最合适的评估策略,是每一位AI从业者必备的核心能力。