1 题目
链表中的 临界点 定义为一个 局部极大值点 或 局部极小值点 。
如果当前节点的值 严格大于 前一个节点和后一个节点,那么这个节点就是一个局部极大值点 。
如果当前节点的值 严格小于 前一个节点和后一个节点,那么这个节点就是一个局部极小值点 。
注意:节点只有在同时存在前一个节点和后一个节点的情况下,才能成为一个 局部极大值点 / 极小值点 。
给你一个链表 head ,返回一个长度为 2 的数组[minDistance, maxDistance] ,其中minDistance是任意两个不同临界点之间的最小距离,maxDistance 是任意两个不同临界点之间的最大距离。如果临界点少于两个,则返回 [-1,-1] 。
示例 1:
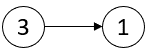
输入:head = [3,1]
输出:[-1,-1]
解释:链表 [3,1] 中不存在临界点。示例 2:

输入:head = [5,3,1,2,5,1,2]
输出:[1,3]
解释:存在三个临界点:
- [5,3,1,2,5,1,2]:第三个节点是一个局部极小值点,因为 1 比 3 和 2 小。
- [5,3,1,2,5,1,2]:第五个节点是一个局部极大值点,因为 5 比 2 和 1 大。
- [5,3,1,2,5,1,2]:第六个节点是一个局部极小值点,因为 1 比 5 和 2 小。
第五个节点和第六个节点之间距离最小。minDistance = 6 - 5 = 1 。
第三个节点和第六个节点之间距离最大。maxDistance = 6 - 3 = 3 。示例 3:
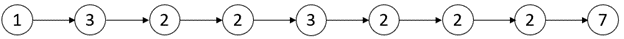
输入:head = [1,3,2,2,3,2,2,2,7]
输出:[3,3]
解释:存在两个临界点:
- [1,3,2,2,3,2,2,2,7]:第二个节点是一个局部极大值点,因为 3 比 1 和 2 大。
- [1,3,2,2,3,2,2,2,7]:第五个节点是一个局部极大值点,因为 3 比 2 和 2 大。
最小和最大距离都存在于第二个节点和第五个节点之间。
因此,minDistance 和 maxDistance 是 5 - 2 = 3 。
注意,最后一个节点不算一个局部极大值点,因为它之后就没有节点了。示例 4:
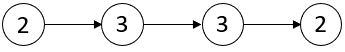
输入:head = [2,3,3,2]
输出:[-1,-1]
解释:链表 [2,3,3,2] 中不存在临界点。2 代码实现
思考
高中导数题目,用链表实现,我看了一下这个题单在链表的遍历里面,最大距离就是第一个临界点和最后的一个临界点之间的距离。最小的距离就是最近的两个临界点距离。
现在要实现的代码有以下难点:
1.如何判断是临界点?
2.怎么存储临界点的"距离"?用数组还是unordered_map?或者用一个count作为计数器?
3.最大的距离或者最小的距离怎么更新?
一点代码都不知道怎么写,只知道循环条件是while ( -> next ! = nullptr)。
这个情况还是先看题解吧(cpp实现)
代码
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
vector<int> nodesBetweenCriticalPoints(ListNode* head) {
// 存储所有临界点的位置(从1开始计数)
vector<int> criticalPositions;
// 边界处理:链表长度小于3时,直接返回[-1,-1]
if (head == nullptr || head->next == nullptr || head->next->next == nullptr) {
return {-1, -1};
}
ListNode* prev = head; // 前一个节点
ListNode* curr = head->next; // 当前节点(从第二个节点开始)
int pos = 2; // 当前节点的位置(第二个节点是位置2)
// 遍历条件:当前节点必须有后一个节点才能判断临界点
while (curr != nullptr && curr->next != nullptr) {
ListNode* nextNode = curr->next;
// 判断是否是局部极大值或极小值
bool isMax = (curr->val > prev->val) && (curr->val > nextNode->val);
bool isMin = (curr->val < prev->val) && (curr->val < nextNode->val);
// 是临界点则记录位置
if (isMax || isMin) {
criticalPositions.push_back(pos);
}
// 指针后移,位置计数+1
prev = curr;
curr = nextNode;
pos++;
}
// 临界点数量不足2个,返回[-1,-1]
if (criticalPositions.size() < 2) {
return {-1, -1};
}
// 计算最大距离:最后一个临界点 - 第一个临界点
int maxDist = criticalPositions.back() - criticalPositions[0];
// 计算最小距离:遍历相邻临界点的差值,取最小值
int minDist = INT_MAX;
for (int i = 1; i < criticalPositions.size(); i++) {
minDist = min(minDist, criticalPositions[i] - criticalPositions[i-1]);
}
return {minDist, maxDist};
}
};3 题解
一、题目理解与核心思路
你一开始提到这道题像高中导数的极值问题,且明确了两个关键结论:
- 最大距离 = 第一个临界点位置 - 最后一个临界点位置;
- 最小距离 = 相邻临界点之间的最小距离;这两个结论是解题的核心,我们的代码也会围绕这个核心展开。
题目核心要求
- 临界点定义:仅存在 "前一个节点" 和 "后一个节点" 的中间节点,且满足 "局部极大值(当前值 > 前后)" 或 "局部极小值(当前值 < 前后)";
- 输出要求:若临界点数量 < 2,返回
[-1,-1];否则返回[最小距离, 最大距离]。
解题关键问题
| 你的疑问 | 解决方案 |
|---|---|
| 如何判断临界点? | 遍历链表时,对每个中间节点(有前驱 + 后继),判断是否满足 "局部极大 / 极小值" 条件 |
| 如何存储临界点? | 用数组(vector)存储临界点的位置索引(从 1 开始计数),无需复杂结构(如 map) |
| 如何更新最小 / 最大距离? | 最大距离:直接取数组首尾元素差值;最小距离:遍历数组计算相邻元素差值的最小值 |
二、完整解题步骤
步骤 1:边界预处理
链表长度 < 3 时(即head/head->next/head->next->next为空),不可能存在临界点,直接返回[-1,-1]。
步骤 2:遍历链表,识别并记录临界点
-
初始化指针:
prev(前驱节点,初始为head)、curr(当前节点,初始为head->next); -
初始化位置计数器:
pos=2(curr是第二个节点,位置从 1 开始); -
遍历条件:
curr != nullptr && curr->next != nullptr(保证当前节点有后继); -
临界点判断:
cppbool isMax = (curr->val > prev->val) && (curr->val > nextNode->val); bool isMin = (curr->val < prev->val) && (curr->val < nextNode->val); -
满足条件则将
pos存入criticalPositions数组。
步骤 3:计算最小 / 最大距离
- 若临界点数量 < 2,返回
[-1,-1]; - 最大距离:
criticalPositions.back() - criticalPositions[0](首尾差值); - 最小距离:遍历数组,计算相邻元素差值的最小值(初始设为
INT_MAX,确保第一次差值能覆盖)。
三、代码逐行解析(结合你的代码框架)
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
#include <vector>
#include <climits> // 提供INT_MAX常量
using namespace std;
class Solution {
public:
vector<int> nodesBetweenCriticalPoints(ListNode* head) {
// 存储临界点的位置(从1开始计数),对应你问的"怎么存储临界点"
vector<int> criticalPositions;
// 边界处理:链表长度<3,无临界点
if (head == nullptr || head->next == nullptr || head->next->next == nullptr) {
return {-1, -1};
}
// 初始化指针:prev=前驱节点,curr=当前节点(从第二个节点开始)
ListNode* prev = head;
ListNode* curr = head->next;
int pos = 2; // 当前节点的位置(第二个节点是位置2)
// 遍历条件:你提到的while循环,补充了curr非空的安全判断
while (curr != nullptr && curr->next != nullptr) {
ListNode* nextNode = curr->next; // 后继节点
// 核心:判断临界点(对应你问的"如何判断临界点")
bool isMax = (curr->val > prev->val) && (curr->val > nextNode->val);
bool isMin = (curr->val < prev->val) && (curr->val < nextNode->val);
// 是临界点则记录位置
if (isMax || isMin) {
criticalPositions.push_back(pos);
}
// 指针后移,位置计数+1
prev = curr;
curr = nextNode;
pos++;
}
// 临界点数量不足2个,返回[-1,-1]
if (criticalPositions.size() < 2) {
return {-1, -1};
}
// 计算最大距离:你总结的"第一个和最后一个临界点的距离"
int maxDist = criticalPositions.back() - criticalPositions[0];
// 计算最小距离:你总结的"最近的两个临界点距离"
int minDist = INT_MAX; // 初始化为极大值
for (int i = 1; i < criticalPositions.size(); i++) {
minDist = min(minDist, criticalPositions[i] - criticalPositions[i-1]);
}
return {minDist, maxDist};
}
};四、测试用例验证
示例 2:输入[5,3,1,2,5,1,2]
- 临界点位置:3(1<3 且 1<2)、5(5>2 且 5>1)、6(1<5 且 1<2);
- 最大距离:6-3=3;
- 最小距离:6-5=1;
- 输出:
[1,3],符合预期。
示例 3:输入[1,3,2,2,3,2,2,2,7]
- 临界点位置:2(3>1 且 3<2?不,3>1 且 3>2,是极大值)、5(3>2 且 3>2,是极大值);
- 最大 / 最小距离:5-2=3;
- 输出:
[3,3],符合预期。
4 小结
- 临界点判断:仅中间节点(有前驱 + 后继)能成为临界点,需满足 "严格大于 / 小于前后节点";
- 存储策略:用数组存储临界点位置(从 1 计数),是最简单高效的方式;
- 距离计算:最大距离 = 首尾临界点位置差,最小距离 = 相邻临界点位置差的最小值;
- 边界处理 :链表长度 < 3、临界点数量 < 2 时,均返回
[-1,-1]。
这道题的核心是链表的顺序遍历 +极值判断 +简单的数组遍历计算,你的初始思考已经抓住了最关键的距离计算逻辑,只需要补充临界点判断和存储的细节即可。
自己把代码清空了重写一遍,思路很明白,就是自己写不来,看得懂写不来。
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
vector<int> nodesBetweenCriticalPoints(ListNode* head) {
vector<int> criticalPos ;
if(head == nullptr || head -> next == nullptr || head -> next -> next == nullptr){
return {-1 , -1 };
}
ListNode* prev = head ;
ListNode* cur = head -> next ;
int pos = 2 ;
while (cur != nullptr && cur -> next != nullptr){
bool isMax = (cur -> val > prev -> val) &&(cur -> val > cur -> next -> val);
bool isMin = (cur -> val < prev -> val) && (cur -> val < cur -> next -> val);
if (isMax || isMin){
criticalPos.push_back(pos);
}
prev = cur ;
cur = cur -> next ;
pos++;
}
if(criticalPos.size() < 2){
return{ -1 , -1 };
}
int maxDistance = criticalPos.back() - criticalPos[0];
int minDistance = INT_MAX;
for (int i = 1 ; i < criticalPos.size() ; i++){
minDistance = min (criticalPos[i] - criticalPos[i - 1],minDistance);
}
return{minDistance,maxDistance};
}
};手写错误小结
我自己写有几个错误,但是我纠正过来了,下面是我写的错误。
1.循环逻辑放的位置不对,
if(criticalPos.size() < 2){
return{ -1 , -1 };
}
我把这段错误的嵌套在放入数组的循环里面了
2.逻辑表达Boolean没写清楚
bool isMax = (cur -> val > prev -> val) &&(cur -> val > cur -> next -> val);
我一开始没有加这两个小括号
3. 数组的末尾函数乱写,我
int maxDistance = criticalPos.back() - criticalPos[0];
我自己写的是.end(),其实是.back()
把 criticalPos.back() 写成 criticalPos.end(),导致编译错误 / 逻辑错误。
本质原因
对 STL 容器的常用函数记忆模糊:
| 函数 | 返回值 | 用途 |
|---|---|---|
.end() |
迭代器(指向容器末尾的下一个位置) | 遍历结束标记(如 for 循环) |
.back() |
容器最后一个元素的引用 | 获取最后一个元素的值 |
.front() |
容器第一个元素的引用 | 获取第一个元素的值 |
避坑方法
记核心函数 + 手写小例子:
cpp
// 随手写测试,强化记忆
vector<int> vec = {3,5,6};
cout << vec.front(); // 输出3(第一个元素)
cout << vec.back(); // 输出6(最后一个元素)
// cout << vec.end(); // 错误:end()是迭代器,不能直接输出值写代码时,只要是 "取容器首尾元素的值",就用 .front()/.back();只要是 "遍历的结束位置",才用 .end()。
解决 "看得懂写不来" 的核心方法
你现在的问题不是 "思路不懂",而是 "动手少、细节不熟练",按以下步骤练,1-2 周就能明显改善:
步骤 1:"拆解式仿写"(从抄到写的过渡)
拿到一道题,先不直接写完整代码,而是:
- 把解题步骤拆成 5-8 个小任务(比如 "初始化指针""判断临界点""计算最大距离");
- 先写第一个小任务,运行确认没错;
- 再写第二个,以此类推。比如这道题,你可以先只写 "遍历链表 + 判断临界点",打印出临界点位置,确认正确后,再加 "计算距离" 的逻辑。
步骤 2:"刻意记细节"(针对你犯的语法错误)
把你容易错的点整理成 "错题本",比如:
- vector 常用函数:
back()/front()/size()/push_back(); - 逻辑表达式必须加括号;
- 条件判断的位置(比如数量判断要在收集完数据后);每天花 5 分钟看一遍,写代码时刻意提醒自己。
步骤 3:"无参考重写"(关键步骤)
看懂题解后,关闭题解,自己从头写一遍:
- 第一遍错了没关系,记下来错在哪;
- 隔 1 小时再写第二遍,直到能一次写对。这道题你已经做到了 "自己写 + 纠正错误",这是最有价值的一步 ------ 错误比正确更重要,因为你找到了自己的薄弱点。
- 逻辑结构:判断临界点数量的代码必须放在遍历链表之后,先 "收集数据" 再 "判断处理";
- 语法细节 :复合布尔表达式加括号,vector 取首尾元素用
back()/front()(而非end()); - 练习方法:解决 "看得懂写不来" 的核心是 "拆解任务 + 刻意记细节 + 无参考重写",而非 "看更多题解"。