【DeepSeek论文精读】14. mHC：流形约束超连接

欢迎关注【AIGC论文精读】原创作品
【DeepSeek论文精读】1. 从 DeepSeek LLM 到 DeepSeek R1
【DeepSeek论文精读】13. DeepSeek-Coder-V2: 突破闭源模型在代码智能领域的障碍
 【DeepSeek论文精读】14. mHC：流形约束超连接

【DeepSeek论文精读】14. mHC：流形约束超连接

- [0. 论文简介](#0. 论文简介)
- - [0.1 论文背景](#0.1 论文背景)
  - [0.2 总结速览](#0.2 总结速览)
  - [0.3 摘要](#0.3 摘要)
- [1. 引言](#1. 引言)
- [2. 相关研究](#2. 相关研究)
- - [2.1 微观设计](#2.1 微观设计)
  - [2.2 宏观设计](#2.2 宏观设计)
- [3. 预备知识](#3. 预备知识)
- - [3.1 数值不稳定](#3.1 数值不稳定)
  - [3.2 系统开销](#3.2 系统开销)
- [4. 方法](#4. 方法)
- - [4.1 流形约束超连接](#4.1 流形约束超连接)
  - [4.2 参数化与流形投影](#4.2 参数化与流形投影)
  - [4.3 高效基础设施设计](#4.3 高效基础设施设计)
  - - [4.3.1 内核融合](#4.3.1 内核融合)
    - [4.3.2 重计算](#4.3.2 重计算)
    - [4.3.3 DualPipe 通信重叠](#4.3.3 DualPipe 通信重叠)
- [5. 方法](#5. 方法)
- - [5.1. 实验设置](#5.1. 实验设置)
  - [5.2. 主要结果](#5.2. 主要结果)
  - [5.3. 扩展实验](#5.3. 扩展实验)
  - [5.4. 稳定性分析](#5.4. 稳定性分析)
- [6. 结论与展望](#6. 结论与展望)
- [附录：A.1. 详细模型规格与超参数](#附录：A.1. 详细模型规格与超参数)
- 参考文献

0. 论文简介

0.1 论文背景

2025年12月31日，DeepSeek 公布了一篇新论文 "mHC：流形约束超连接（mHC: Manifold-Constrained Hyper-Connections）"。

Z. Xie, Y. et al. and W. Liang, "mHC: Manifold-constrained hyper-connections," arXiv preprint arXiv:2512.24880, Dec. 2025. doi: 10.48550/arXiv.2512.24880.

本文提出名为 mHC （流形约束超连接）的新架构，旨在解决传统超连接在大规模模型训练中的不稳定性问题，同时保持其显著的性能增益。

【论文下载】： arxiv

0.2 总结速览

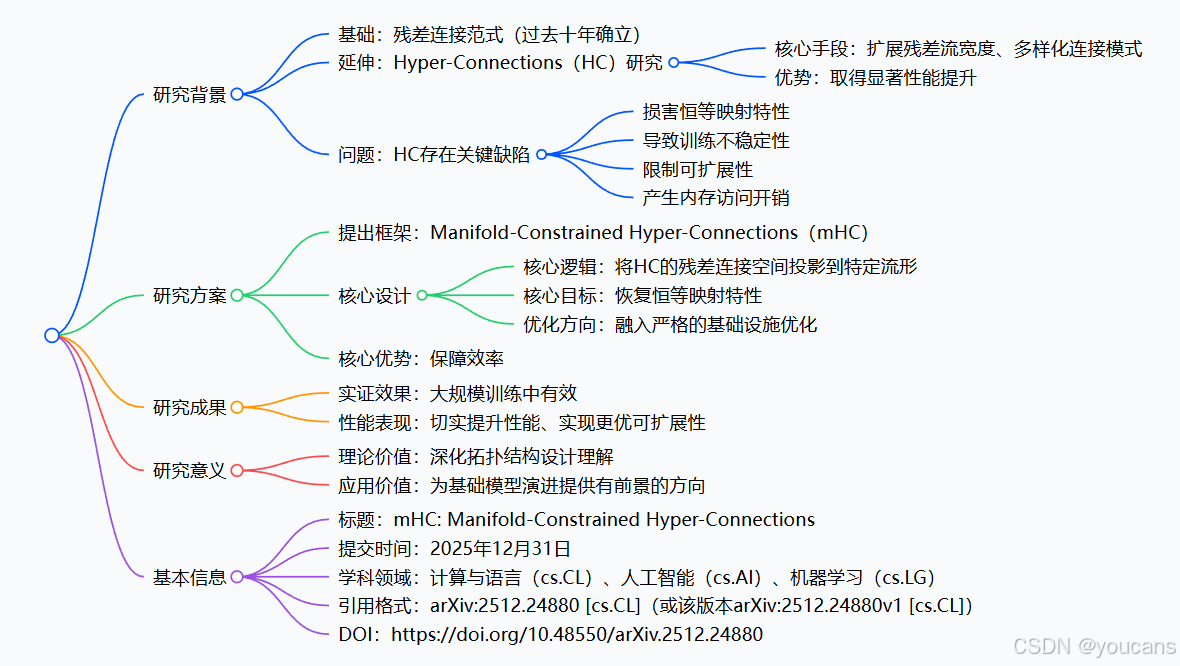
0.3 摘要

最近，由超连接 (HC) 为代表的研究通过扩展残差流宽和多样化连接模式，扩展了残差连接范式。虽然这种多样化带来了显著的性能提升，但从根本上破坏了残差连接固有的恒等映射属性，导致严重的训练不稳定性、受限的可扩展性，并且还会引入显著的内存访问开销。

为了解决这些挑战，我们提出了一种流形约束超连接 (mHC) 的通用框架，该框架将 HC 的残差连接空间投影到特定的流形上，以恢复恒等映射属性，并结合严格的基础设施优化以确保效率。

实验证明，mHC 在大规模训练中是有效的，提供了实际的性能提升和更好的可扩展性。我们预期，作为 HC 的灵活且实用的扩展，mHC 将有助于更深入地理解拓扑架构设计，并为基础模型的演变指出有希望的方向。

1. 引言

深度神经网络架构自 ResNet 被提出以来经历了快速演进。如图 1(a) 所示，单层的结构可表示为：

x l + 1 = x l + F ( x l , W l ) , (1) \mathbf{x}{l+1}=\mathbf{x}{l}+\mathcal{F}(\mathbf{x}{l},\mathcal{W}{l}) , \tag{1} xl+1=xl+F(xl,Wl),(1)

其中 x l \mathbf{x}{l} xl 与 x l + 1 \mathbf{x}{l+1} xl+1 分别表示第 l l l 层的 C C C 维输入与输出， F \mathcal{F} F 代表残差函数。尽管在过去十年中残差函数 F \mathcal{F} F 已从卷积、注意力机制到前馈网络不断演化，残差连接本身的形式却始终未变。随着 Transformer 架构的兴起，这一范式已成为当今大型语言模型（LLMs）的基础设计元素。

其成功主要归功于残差连接的简洁性。更重要的是，早期研究指出，残差连接的恒等映射特性在大规模训练过程中保证了稳定性与效率。将残差连接递归地扩展到多层，可得

x L = x l + ∑ i = l L − 1 F ( x i , W i ) , (2) \mathbf{x}{L}=\mathbf{x}{l}+\sum_{i=l}^{L-1}\mathcal{F}(\mathbf{x}{i},\mathcal{W}{i}), \tag{2} xL=xl+i=l∑L−1F(xi,Wi),(2)

其中 L L L 与 l l l 分别对应更深与更浅的层。所谓恒等映射即指 x l \mathbf{x}_{l} xl 本身，它强调浅层信号无需任何修改即可直接传递至更深层。

近期，以超连接（Hyper-Connections, HC）为代表的研究为残差连接引入了新维度，并在实证中展现了性能潜力。图 1(b) 展示了 HC 的单层架构：通过拓宽残差流的宽度并增加连接复杂性，HC 在不改变单个计算单元 FLOPs 的前提下显著提升了拓扑复杂度。形式上，HC 的单层传播定义为

x l + 1 = H l r e s x l + H l p o s t ⊤ F ( H l p r e x l , W l ) , (3) \mathbf{x}{l+1}=\mathcal{H}{l}^{\mathrm{res}}\mathbf{x}{l}+\mathcal{H}{l}^{\mathrm{post}\top}\mathcal{F}(\mathcal{H}{l}^{\mathrm{pre}}\mathbf{x}{l},\mathcal{W}_{l}), \tag{3} xl+1=Hlresxl+Hlpost⊤F(Hlprexl,Wl),(3)

其中 x l \mathbf{x}{l} xl 与 x l + 1 \mathbf{x}{l+1} xl+1 分别为第 l l l 层的输入与输出。与式 (1) 不同， x l \mathbf{x}{l} xl 与 x l + 1 \mathbf{x}{l+1} xl+1 的特征维度由 C C C 扩展至 n × C n\times C n×C， n n n 为扩展率。 H l r e s ∈ R n × n \mathcal{H}{l}^{\mathrm{res}}\in\mathbb{R}^{n\times n} Hlres∈Rn×n 为可学映射，用于在残差流内部混合特征； H l p r e ∈ R 1 × n \mathcal{H}{l}^{\mathrm{pre}}\in\mathbb{R}^{1\times n} Hlpre∈R1×n 与 H l p o s t ∈ R 1 × n \mathcal{H}_{l}^{\mathrm{post}}\in\mathbb{R}^{1\times n} Hlpost∈R1×n 亦为可学映射，分别负责将 n C nC nC 维流聚合为 C C C 维层输入，以及将层输出映射回流空间。

然而，随着训练规模扩大，HC 带来了潜在的不稳定风险。首要问题在于，HC 的无约束特性在多层堆叠时破坏了恒等映射性质。在包含多条并行流的架构中，理想的恒等映射起到守恒作用：确保前向与反向传播过程中各流信号强度的平均值保持不变。将 HC 递归地扩展到多层，可得

x L = ( ∏ i = 1 L − l H L − i r e s ) x l + ∑ i = l L − 1 ( ∏ j = 1 L − 1 − i H L − j r e s ) H i p o s t ⊤ F ( H i p r e x i , W i ) , (4) \mathbf{x}{L}=\left(\prod{i=1}^{L-l}\mathcal{H}{L-i}^{\mathrm{res}}\right)\mathbf{x}{l}+\sum_{i=l}^{L-1}\left(\prod_{j=1}^{L-1-i}\mathcal{H}{L-j}^{\mathrm{res}}\right)\mathcal{H}{i}^{\mathrm{post}\top}\mathcal{F}(\mathcal{H}{i}^{\mathrm{pre}}\mathbf{x}{i},\mathcal{W}_{i}), \tag{4} xL=(i=1∏L−lHL−ires)xl+i=l∑L−1(j=1∏L−1−iHL−jres)Hipost⊤F(Hiprexi,Wi),(4)

其中 L L L 与 l l l 分别对应更深与更浅的层。与式 (2) 相比，HC 中的复合映射 ∏ i = 1 L − l H L − i r e s \prod_{i=1}^{L-l}\mathcal{H}_{L-i}^{\mathrm{res}} ∏i=1L−lHL−ires 无法保持特征的全局均值，导致信号无界放大或衰减，进而引发大规模训练中的不稳定性。此外，尽管 HC 在 FLOPs 层面保持了计算效率，其拓宽的残差流在硬件层面的内存访问开销却未在原设计中加以解决。这些因素共同限制了 HC 的实际可扩展性，阻碍了其在大规模训练中的应用。

为应对上述挑战，我们提出"流形约束超连接"（Manifold-Constrained Hyper-Connections, mHC），如图 1© 所示。该通用框架将 HC 的残差连接空间投影至特定流形，以恢复恒等映射性质，并通过严谨的基础设施优化确保效率。具体而言，mHC 利用 Sinkhorn--Knopp 算法将 H l r e s \mathcal{H}{l}^{\mathrm{res}} Hlres 熵投影到 Birkhoff 多面体，从而把残差连接矩阵约束为双随机矩阵。由于双随机矩阵行列和均为 1，操作 H l r e s x l \mathcal{H}{l}^{\mathrm{res}}\mathbf{x}{l} Hlresxl 相当于对输入特征做凸组合，能够在严格正则化信号范数的同时保持特征均值不变，有效缓解梯度爆炸或消失风险。此外，双随机矩阵在矩阵乘法下封闭，因此复合映射 ∏ i = 1 L − l H L − i r e s \prod{i=1}^{L-l}\mathcal{H}_{L-i}^{\mathrm{res}} ∏i=1L−lHL−ires 仍保持双随机性，使得任意深度之间的恒等映射稳定性得以维持。

为保证效率，我们采用内核融合技术，并利用 TileLang 开发混合精度内核；同时通过选择性重计算以及在 DualPipe 调度中精细重叠通信，进一步降低内存占用。语言模型预训练的广泛实验表明，mHC 在保持稳定性的同时，具备出色的扩展性，且相比 HC 仅引入约 6.7% 的额外训练时间（当扩展率 n = 4 n=4 n=4 时）。

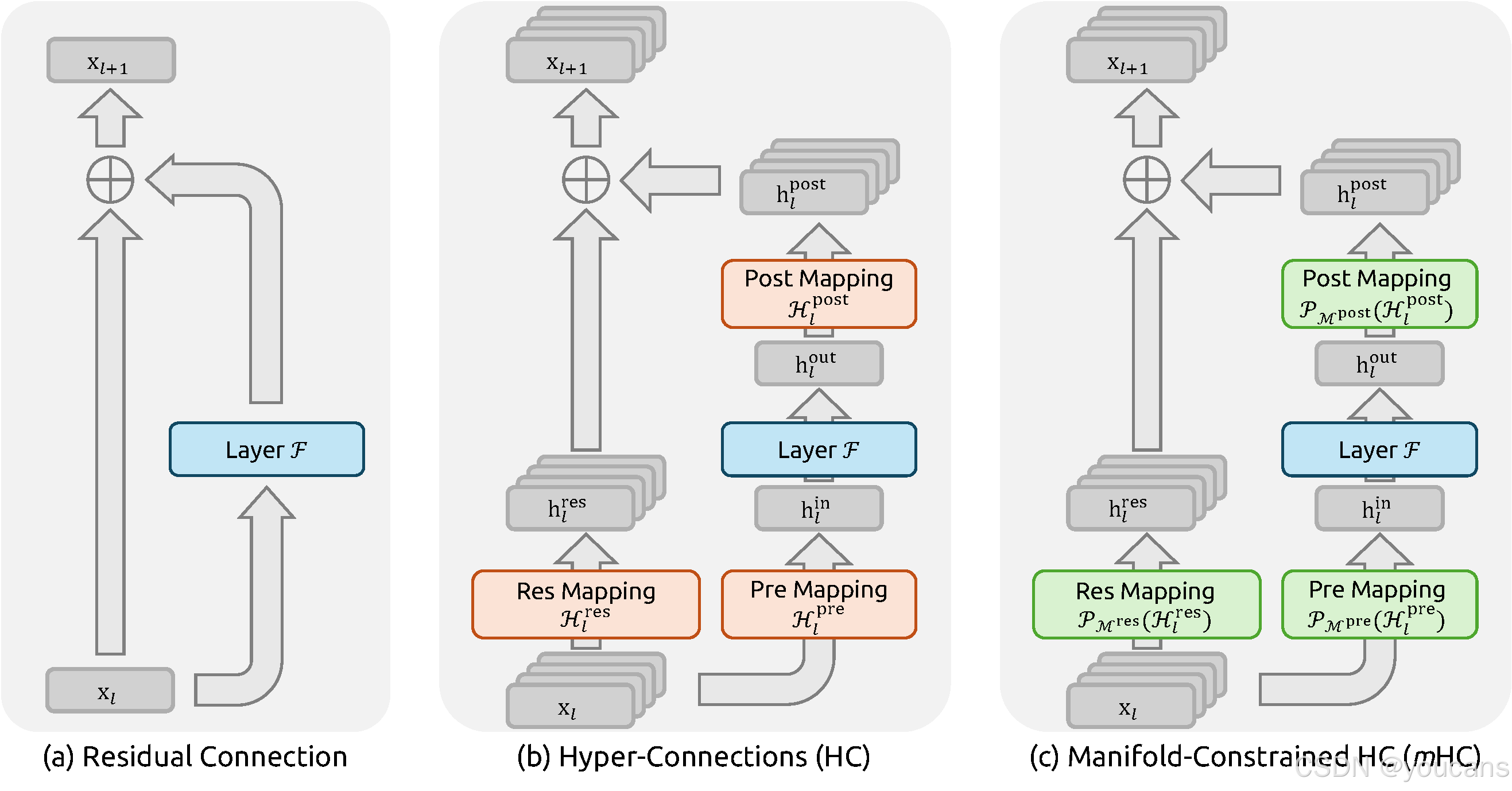
图1 | 残差连接范式的示意图。
此图比较了(a) 标准残差连接，(b) 超连接 (HC)，以及© 我们提出的手约束超连接 (mHC)。
与未约束的 HC 不同，mHC 通过将矩阵投影到约束流形上来优化残差连接空间，以确保稳定性。

2. 相关研究

深度学习的架构进步大体可分为"微观设计"与"宏观设计"两类。微观设计关注计算模块内部的结构，规定特征如何在空间、时间或通道维度上被处理；宏观设计则定义跨模块的全局拓扑，决定特征表示如何沿不同层级传播、路由与融合。

2.1 微观设计

受参数共享与平移不变性驱动，卷积最初在结构化信号处理中占据主导。随后，深度可分离卷积与分组卷积等变体提升了效率。Transformer 的出现确立了注意力与前馈网络（FFN）作为现代架构的基本构件：注意力机制实现全局信息传播，FFN 则增强单个特征的表示能力。为了在性能与 LLM 计算开销之间取得平衡，注意力机制演化出多查询注意力（MQA）、分组查询注意力（GQA）与多头潜在注意力（MLA）等高效变体；与此同时，FFN 通过专家混合（MoE）被推广到稀疏计算范式，在不同比增加计算成本的前提下实现参数的大规模扩展。

2.2 宏观设计

宏观设计决定网络的全局拓扑。继 ResNet 之后，DenseNet、FractalNet 等架构通过密集连接或多路径结构提升拓扑复杂度，从而提高性能。深度层聚合（DLA）进一步递归地在不同深度与分辨率之间聚合特征。

近期，宏观设计的焦点转向"拓宽残差流宽度"。Hyper-Connections（HC）引入可学习矩阵来调制不同深度特征间的连接强度；Residual Matrix Transformer（RMT）用外积记忆矩阵替换标准残差流以存储特征；MUDDFormer 采用多路动态密集连接优化跨层信息流。尽管这些方法潜力巨大，它们都牺牲了残差连接固有的恒等映射特性，导致训练不稳定并阻碍扩展，同时因特征宽度增加带来显著的内存访问开销。

本文提出的 mHC 在 HC 基础上，将残差连接空间约束到特定流形以恢复恒等映射特性，并结合严谨的基础设施优化确保效率，从而在保持扩展连接拓扑优势的同时提升稳定性与可扩展性。

3. 预备知识

本章首先建立本文记号，随后分析 HC 在数值与系统层面存在的两大问题：数值不稳定（3.1）与系统开销（3.2）。

在 HC 的表述中，第 l l l 层的输入 x l ∈ R 1 × C \mathbf{x}_l\in\mathbb{R}^{1\times C} xl∈R1×C 被扩展 n n n 倍，构造隐矩阵

x l = ( x l , 0 ⊤ , ... , x l , n − 1 ⊤ ) ⊤ ∈ R n × C \mathbf{x}l=(\mathbf{x}{l,0}^\top,\dots,\mathbf{x}_{l,n-1}^\top)^\top\in\mathbb{R}^{n\times C} xl=(xl,0⊤,...,xl,n−1⊤)⊤∈Rn×C

可视为 n n n 路残差流，从而拓宽残差宽度。为了管理该流的读入、写出与更新，HC 引入三个可学习线性映射
H l p r e , H l p o s t ∈ R 1 × n , H l r e s ∈ R n × n , \mathcal{H}_l^{\mathrm{pre}},\ \mathcal{H}_l^{\mathrm{post}}\in\mathbb{R}^{1\times n},\quad \mathcal{H}_l^{\mathrm{res}}\in\mathbb{R}^{n\times n}, Hlpre, Hlpost∈R1×n,Hlres∈Rn×n,

将标准残差连接 (1) 修改为式 (3)。这些映射由动态系数与全局（静态）系数共同组成，具体计算为
{ x ~ l = R M S N o r m ( x l ) , H l p r e = α l p r e tanh ⁡ ( θ l p r e x ~ l ⊤ ) + b l p r e , H l p o s t = α l p o s t tanh ⁡ ( θ l p o s t x ~ l ⊤ ) + b l p o s t , H l r e s = α l r e s tanh ⁡ ( θ l r e s x ~ l ⊤ ) + b l r e s , (5) \left\{ \begin{aligned} \tilde{\mathbf{x}}_l &= \mathrm{RMSNorm}(\mathbf{x}_l),\\ \mathcal{H}_l^{\mathrm{pre}} &=\alpha_l^{\mathrm{pre}} \tanh(\boldsymbol{\theta}_l^{\mathrm{pre}} \tilde{\mathbf{x}}_l^\top)+\mathbf{b}_l^{\mathrm{pre}},\\ \mathcal{H}_l^{\mathrm{post}} &=\alpha_l^{\mathrm{post}}\tanh(\boldsymbol{\theta}_l^{\mathrm{post}}\tilde{\mathbf{x}}_l^\top)+\mathbf{b}_l^{\mathrm{post}},\\ \mathcal{H}_l^{\mathrm{res}} &=\alpha_l^{\mathrm{res}} \tanh(\boldsymbol{\theta}_l^{\mathrm{res}} \tilde{\mathbf{x}}_l^\top)+\mathbf{b}_l^{\mathrm{res}}, \end{aligned}\right.\tag{5} ⎩ ⎨ ⎧x~lHlpreHlpostHlres=RMSNorm(xl),=αlpretanh(θlprex~l⊤)+blpre,=αlposttanh(θlpostx~l⊤)+blpost,=αlrestanh(θlresx~l⊤)+blres,(5)

其中 RMSNorm 沿最后一维执行； α l p r e , α l p o s t , α l r e s ∈ R \alpha_l^{\mathrm{pre}},\alpha_l^{\mathrm{post}},\alpha_l^{\mathrm{res}}\in\mathbb{R} αlpre,αlpost,αlres∈R 为可学门控，初始值较小。动态映射通过线性投影 θ l p r e , θ l p o s t ∈ R 1 × C \boldsymbol{\theta}_l^{\mathrm{pre}},\boldsymbol{\theta}_l^{\mathrm{post}}\in\mathbb{R}^{1\times C} θlpre,θlpost∈R1×C 和 θ l r e s ∈ R n × C \boldsymbol{\theta}_l^{\mathrm{res}}\in\mathbb{R}^{n\times C} θlres∈Rn×C 获得，静态映射由可学偏置 b l p r e , b l p o s t ∈ R 1 × n \mathbf{b}_l^{\mathrm{pre}},\mathbf{b}_l^{\mathrm{post}}\in\mathbb{R}^{1\times n} blpre,blpost∈R1×n 和 b l r e s ∈ R n × n \mathbf{b}_l^{\mathrm{res}}\in\mathbb{R}^{n\times n} blres∈Rn×n 表示。

值得注意的是，引入这三个映射带来的计算开销可忽略，因为扩展率 n n n（例如 4）远小于输入维度 C C C。该设计使残差流的信息容量与层的输入维度解耦，而后者与模型 FLOPs 强相关。因此，HC 通过调整残差流宽度为扩展提供了新维度，补充了传统基于 FLOPs 与数据量的预训练扩展律。

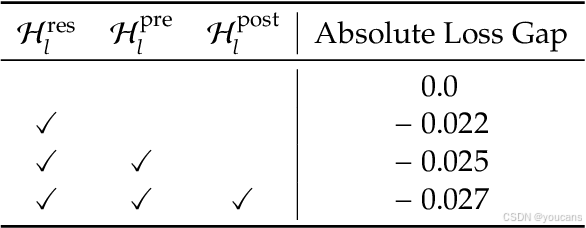
表 1 的初步实验表明，在三个映射中 H l r e s \mathcal{H}_l^{\mathrm{res}} Hlres 对性能提升最为关键，这凸显了残差流内部有效信息交换的重要性。

表1｜HC 组件消融研究。
当禁用某一映射 ( H l p r e (\mathcal{H}_l^{\mathrm{pre}} (Hlpre、 H l p o s t \mathcal{H}_l^{\mathrm{post}} Hlpost 或 H l r e s ) \mathcal{H}_l^{\mathrm{res}}) Hlres) 时，我们采用固定映射保持维度一致： H l p r e \mathcal{H}_l^{\mathrm{pre}} Hlpre 用均匀权重 1 / n 1/n 1/n， H l p o s t \mathcal{H}_l^{\mathrm{post}} Hlpost 用全 1 权重， H l r e s \mathcal{H}_l^{\mathrm{res}} Hlres 用单位矩阵。

3.1 数值不稳定

尽管残差映射 H l r e s \mathcal{H}l^{\mathrm{res}} Hlres 对性能至关重要，其逐层递归应用却带来显著的数值风险。由式 (4) 可知，当 HC 跨多层展开时，层 l l l 到层 L L L 的有效信号传播由复合映射 ∏ i = 1 L − l H L − i r e s \prod{i=1}^{L-l}\mathcal{H}_{L-i}^{\mathrm{res}} ∏i=1L−lHL−ires 控制。由于该映射无约束，复合结果必然偏离恒等映射，导致信号在前向与反向传播中爆炸或消失，从而破坏残差学习依赖的"畅通信号流"前提，使更深或更大模型的训练失稳。

实证观察支持该分析：以 mHC 为基线，HC 在约 12k 步时出现意外的损失激增，且与梯度范数震荡高度相关。为量化复合映射对残差流的放大效应，我们采用两项指标：

前行信号增益：复合映射行和绝对值的最大值；
反向梯度增益：列和绝对值的最大值。
二者合称复合映射的 Amax 增益幅度。图 3(b) 显示，该指标在 HC 中峰值高达 3000，与理想值 1 相差甚远，证实了残差流爆炸的存在。

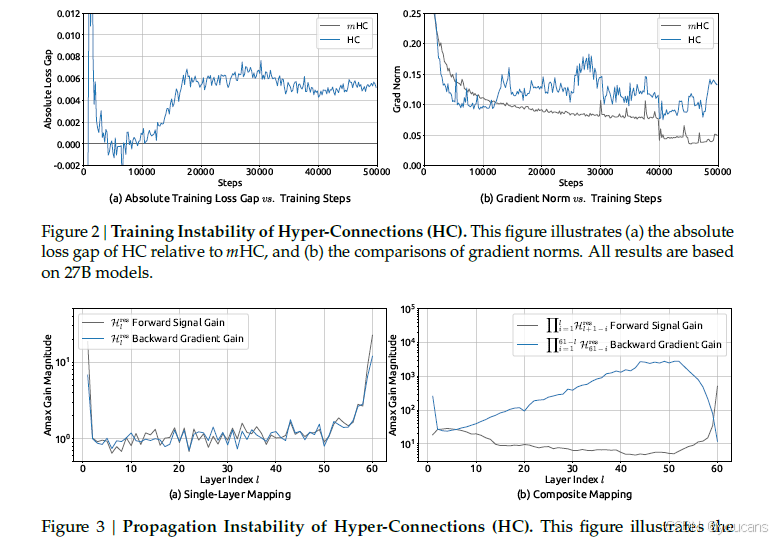
图3｜超连接（HC）的传播不稳定性。
该图展示了 27B 模型内 (a) 单层映射 H l r e s \mathcal{H}{l}^{\mathrm{res}} Hlres 与 (b) 复合映射 ∏ i = 1 L − l H L − i r e s \prod{i=1}^{L-l}\mathcal{H}_{L-i}^{\mathrm{res}} ∏i=1L−lHL−ires 的传播动态。
横轴为层索引（每个标准 Transformer 块拆分为 Attention 与 FFN 两个独立层），纵轴为 Amax 增益幅度：前行信号取行和绝对值最大，反向梯度取列和绝对值最大，并在所选序列的所有令牌上取平均。

3.2 系统开销

尽管 HC 的额外映射在 FLOPs 层面开销有限，其系统级代价却不容忽视。在现代架构中，内存访问（I/O）常成为首要瓶颈，即所谓"内存墙"。该瓶颈常被架构设计忽视，却显著影响实际运行效率。

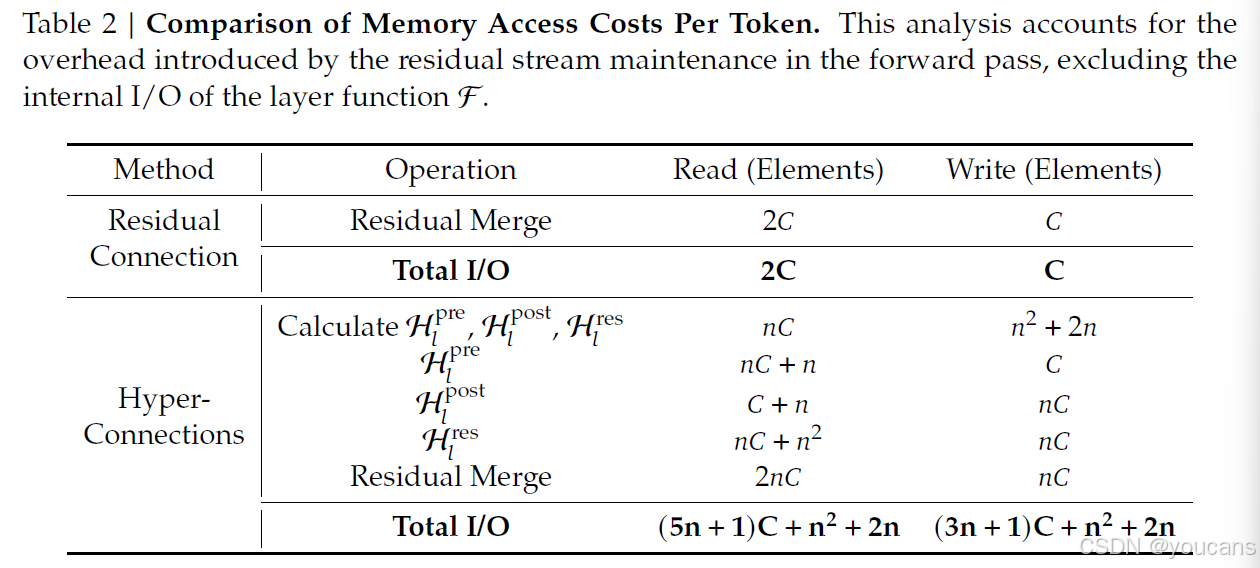
针对广泛采用的前归一化 Transformer，我们分析了 HC 引入的每令牌内存访问开销。表 2 显示，HC 使单残差层的读写成本大约放大 n n n 倍。若未采用融合内核，这种过度 I/O 需求会显著降低训练吞吐。此外，由于 H l p r e , H l p o s t , H l r e s \mathcal{H}_l^{\mathrm{pre}},\mathcal{H}_l^{\mathrm{post}},\mathcal{H}_l^{\mathrm{res}} Hlpre,Hlpost,Hlres 包含可学参数，反向传播需保存其中间激活，进一步增加 GPU 内存占用，往往必须启用梯度检查点才能维持可行内存使用。同时，HC 在流水线并行中的通信量也增加约 n n n 倍，导致更大气泡并降低训练吞吐。

表2｜每令牌内存访问成本对比。
本表统计前向传播中因维护残差流而引入的读写开销，不含层函数 F \mathcal{F} F 内部的 I/O。

4. 方法

为恢复被 HC 破坏的恒等映射性质，同时保留拓宽残差流带来的拓扑优势，我们提出"流形约束超连接"（mHC）。本章先给出 mHC 的核心思想（4.1），随后详细阐述参数化与流形投影（4.2），最后介绍面向大规模训练的高效基础设施设计（4.3）。

4.1 流形约束超连接

受恒等映射原理启发，mHC 将残差映射 H l r e s \mathcal{H}_l^{\mathrm{res}} Hlres 约束在特定流形上。原始恒等映射强制 H l r e s = I \mathcal{H}_l^{\mathrm{res}}=\mathbf{I} Hlres=I 虽能保证稳定，却禁止残差流内部的信息交换，难以发挥多路架构的潜力。为此，我们把 H l r e s \mathcal{H}_l^{\mathrm{res}} Hlres 投影到"双随机矩阵流形"（即 Birkhoff 多面体），使其同时满足：

非负性；
行和与列和均为 1。

形式化地，令 M r e s \mathcal{M}^{\mathrm{res}} Mres 表示双随机矩阵流形，投影算子定义为
P M r e s ( H l r e s ) : = { H l r e s ∈ R n × n ∣ H l r e s 1 n = 1 n , 1 n ⊤ H l r e s = 1 n ⊤ , H l r e s ≥ 0 } , (6) \mathcal{P}_{\mathcal{M}^{\mathrm{res}}}(\mathcal{H}_l^{\mathrm{res}}):=\left\{\mathcal{H}_l^{\mathrm{res}}\in\mathbb{R}^{n\times n}\mid\mathcal{H}_l^{\mathrm{res}}\mathbf{1}_n=\mathbf{1}_n,\;\mathbf{1}_n^\top\mathcal{H}_l^{\mathrm{res}}=\mathbf{1}_n^\top,\;\mathcal{H}_l^{\mathrm{res}}\geq 0\right\}, \tag{6} PMres(Hlres):={Hlres∈Rn×n∣Hlres1n=1n,1n⊤Hlres=1n⊤,Hlres≥0},(6)

其中 1 n \mathbf{1}_n 1n 为全 1 向量。当 n = 1 n=1 n=1 时，双随机条件退化为标量 1，恰好回到原始恒等映射。

双随机性带来三项理论保证：

范数保持：谱范数 ∥ H l r e s ∥ 2 ≤ 1 \|\mathcal{H}_l^{\mathrm{res}}\|_2\leq 1 ∥Hlres∥2≤1，映射非扩张，抑制梯度爆炸；
复合封闭：双随机矩阵在乘法下封闭，因此深度复合映射仍保持双随机，维持全模型稳定性；
几何解释：Birkhoff 多面体是置换矩阵的凸包，残差映射可视为置换的凸组合，逐层单调增强信息混合，形成鲁棒的特征融合机制。

此外，我们对输入映射 H l p r e \mathcal{H}_l^{\mathrm{pre}} Hlpre 与输出映射 H l p o s t \mathcal{H}_l^{\mathrm{post}} Hlpost 施加非负约束，防止正负系数相消，也可视为一种特殊流形投影。

4.2 参数化与流形投影

给定第 l l l 层隐矩阵 x l ∈ R n × C \mathbf{x}_l\in\mathbb{R}^{n\times C} xl∈Rn×C，我们先将其展平为向量 x ⃗ l = v e c ( x l ) ∈ R 1 × n C \vec{\mathbf{x}}_l=\mathrm{vec}(\mathbf{x}_l)\in\mathbb{R}^{1\times nC} x l=vec(xl)∈R1×nC 以保留完整上下文。随后沿用 HC 的动态+静态分解：
{ x ⃗ l ′ = R M S N o r m ( x ⃗ l ) , H ~ l p r e = α l p r e ( x ⃗ l ′ φ l p r e ) + b l p r e , H ~ l p o s t = α l p o s t ( x ⃗ l ′ φ l p o s t ) + b l p o s t , H ~ l r e s = α l r e s m a t ( x ⃗ l ′ φ l r e s ) + b l r e s , (7) \left\{ \begin{aligned} \vec{\mathbf{x}}_l' &= \mathrm{RMSNorm}(\vec{\mathbf{x}}_l),\\ \tilde{\mathcal{H}}_l^{\mathrm{pre}} &=\alpha_l^{\mathrm{pre}} (\vec{\mathbf{x}}_l'\boldsymbol{\varphi}_l^{\mathrm{pre}} )+\mathbf{b}_l^{\mathrm{pre}},\\ \tilde{\mathcal{H}}_l^{\mathrm{post}} &=\alpha_l^{\mathrm{post}}(\vec{\mathbf{x}}_l'\boldsymbol{\varphi}_l^{\mathrm{post}})+\mathbf{b}_l^{\mathrm{post}},\\ \tilde{\mathcal{H}}_l^{\mathrm{res}} &=\alpha_l^{\mathrm{res}} \mathrm{mat}(\vec{\mathbf{x}}_l'\boldsymbol{\varphi}_l^{\mathrm{res}} )+\mathbf{b}_l^{\mathrm{res}}, \end{aligned} \right.\tag{7} ⎩ ⎨ ⎧x l′H~lpreH~lpostH~lres=RMSNorm(x l),=αlpre(x l′φlpre)+blpre,=αlpost(x l′φlpost)+blpost,=αlresmat(x l′φlres)+blres,(7)

其中 φ l p r e , φ l p o s t ∈ R n C × n \boldsymbol{\varphi}_l^{\mathrm{pre}},\boldsymbol{\varphi}_l^{\mathrm{post}}\in\mathbb{R}^{nC\times n} φlpre,φlpost∈RnC×n， φ l r e s ∈ R n C × n 2 \boldsymbol{\varphi}_l^{\mathrm{res}}\in\mathbb{R}^{nC\times n^2} φlres∈RnC×n2， m a t ( ⋅ ) \mathrm{mat}(\cdot) mat(⋅) 把 1 × n 2 1\times n^2 1×n2 向量重排成 n × n n\times n n×n 矩阵。

最终约束映射通过
{ H l p r e = σ ( H ~ l p r e ) , H l p o s t = 2 σ ( H ~ l p o s t ) , H l r e s = S i n k h o r n - − K n o p p ( H ~ l r e s ) , (8) \left\{ \begin{aligned} \mathcal{H}_l^{\mathrm{pre}} &=\sigma(\tilde{\mathcal{H}}_l^{\mathrm{pre}}),\\ \mathcal{H}_l^{\mathrm{post}} &=2\sigma(\tilde{\mathcal{H}}_l^{\mathrm{post}}),\\ \mathcal{H}_l^{\mathrm{res}} &=\mathrm{Sinkhorn\textrm--Knopp}(\tilde{\mathcal{H}}_l^{\mathrm{res}}), \end{aligned} \right.\tag{8} ⎩ ⎨ ⎧HlpreHlpostHlres=σ(H~lpre),=2σ(H~lpost),=Sinkhorn-−Knopp(H~lres),(8)

获得，其中 σ ( ⋅ ) \sigma(\cdot) σ(⋅) 为 Sigmoid。Sinkhorn--Knopp 算子先对矩阵元素取指数使其为正，再交替行、列归一化直至收敛，得到双随机矩阵。实际中取最大迭代次数 t max ⁡ = 20 t_{\max}=20 tmax=20。

4.3 高效基础设施设计

本节详细介绍为 mHC 量身定制的基础设施设计。通过严格优化，我们在大规模模型中实现了 mHC（设定 𝑛 = 4），其额外训练开销仅为6.7%。

4.3.1 内核融合

观察到 RMSNorm 在高维隐藏状态 x ⃗ l \vec{\mathbf{x}}_l x l 上延迟显著，mHC 中的 RMSNorm 操作会带来显著延迟。为此，我们将除以范数的操作重新排序至矩阵乘法之后。此优化在保持数学等价性的同时提升了效率。此外，我们采用混合精度策略，在不牺牲速度的前提下最大化数值精度，并将多个具有共享内存访问的操作融合到统一的计算核心中，以减少内存带宽瓶颈。

公式 (10) 至 (13)：基我们实现了三个专用的 mHC 核心来计算 Hpre𝑙、Hpost𝑙 和 Hres𝑙。在这些核心中，偏置项和线性投影被合并到 b𝑙 和 𝜑𝑙 中，RMSNorm 权重也一并融入 𝜑𝑙。
公式 (14) 至 (15)：我们开发了一个统一的核心，融合了对 ®x𝑙 的两次扫描，并利用矩阵乘法单元最大化内存带宽利用率。包含两次矩阵乘法的反向传播过程同样被整合进单一核心，消除了 ®x𝑙 的重复加载。这两个核心都具备精细调度的流水线（加载、类型转换、计算、存储），以高效处理混合精度计算。
公式 (16) 至 (18)：这些作用于小系数的轻量级操作被适时地融合进单一核心，显著降低了核心启动开销。
公式 (19)：我们在单一核心内实现了 Sinkhorn-Knopp 迭代。对于反向传播，我们推导了一个定制的反向核心，它在芯片上重新计算中间结果并遍历整个迭代过程。

利用从上述计算核心中得出的系数，我们引入了两个额外的核心来应用这些映射关系：一个用于计算 Fpre ≔ Hpre𝑙 x𝑙，另一个用于计算 Fpost,res ≔ Hres𝑙 x𝑙 + Hpost⊤𝑙 F (·, ·)。通过将 Hpost𝑙 和 Hres𝑙 的应用与残差合并相融合，我们将该核心从内存中读取的元素数量从 (3𝑛 + 1)𝐶 减少到 (𝑛 + 1)𝐶，并将写入的元素数量从 3𝑛𝐶 减少到 𝑛𝐶。我们使用 TileLang (Wang et al., 2025) 高效地实现了大部分核心（不包括公式 (14) 至 (15)）。该框架简化了具有复杂计算过程的内核实现，使我们能够以最小的工程投入充分利用内存带宽。

4.3.2 重计算

𝑛 流残差设计在训练过程中会引入巨大的内存开销。为缓解此问题，我们在前向传播后丢弃 mHC 核心的中间激活值，并在反向传播期间通过重新执行 mHC 核心（不含计算密集型层函数 F）动态地重新计算它们。因此，对于连续 𝐿𝑟 层的计算块，我们只需存储输入到第一层的激活值 x𝑙0。表 3 总结了为反向传播所保留的中间激活值，其中排除了轻量级系数，并考虑了 F 中的前置归一化操作。

表3｜保存与重计算的中间激活一览
表中列出在连续 L r L_r Lr 层内，每令牌为反向传播而持久保存的激活，以及在块内瞬态重算的激活。层 l 0 l_0 l0 表示该 L r L_r Lr 块的首层，层 l l l 属于 [ l 0 , l 0 + L r − 1 ] [l_0,\,l_0+L_r-1] [l0,l0+Lr−1]。

由于mHC核心重计算是按连续𝐿𝑟层组成的块执行的，在总层数为𝐿的情况下，反向传播时必须为所有⌈𝐿/𝐿𝑟⌉个块持久保存首个层输入x𝑙₀。除了这部分常驻内存外，重计算过程还会为当前计算块引入(𝑛 + 2)𝐶 × 𝐿𝑟个元素的瞬时内存开销，这决定了反向传播期间的峰值内存使用量。因此，我们通过最小化与𝐿𝑟对应的总内存占用量来确定最优块大小 𝐿 𝑟 𝐿_𝑟 Lr：

L r ∗ = arg min ⁡ L r [ n C × ⌈ L L r ⌉ + ( n + 2 ) C × L r ] ≈ n L n + 2 , (20) L_{r}^{*}=\operatorname*{arg\,min}{L{r}}\left[n C\times\left\lceil\frac{L}{L_{r}}\right\rceil+(n+2)C\times L_{r}\right]\approx\sqrt{\frac{n L}{n+2}}, \tag{20} Lr∗=Lrargmin[nC×⌈LrL⌉+(n+2)C×Lr]≈n+2nL ,(20)

此外，大规模训练中的流水线并行技术带来了一项约束：重计算块不得跨越流水线阶段的边界。通过观察发现，理论最优值 𝐿 𝑟 𝐿_𝑟 Lr 通常与每个流水线阶段包含的层数相一致，因此我们选择将重计算边界与流水线阶段边界进行同步对齐。

4.3.3 DualPipe 通信重叠

在大规模训练中，流水线并行是减轻参数和梯度内存占用的标准做法。具体而言，我们采用 DualPipe 调度方案（Liu et al., 2024b），它能有效重叠扩展互连通信流量，例如专家并行和流水线并行中的通信。然而，与单流设计相比，mHC 中提出的 𝑛 流残差结构在跨流水线阶段时会产生显著的通信延迟。此外，在阶段边界处，为所有 𝐿𝑟 层重计算 mHC 核心会带来不可忽略的计算开销。为解决这些瓶颈，我们扩展了 DualPipe 调度方案（见图 4），以促进流水线阶段边界处通信与计算的更好重叠。

值得注意的是，为了防止阻塞通信流，我们在专用的高优先级计算流上执行 MLP（即 FFN）层的 Fpost,res 核心。我们还避免在注意力层中对长时间运行的操作使用持久化核心，从而防止长时间停滞。这种设计使得重叠的注意力计算可以被抢占，从而在保持计算设备处理单元高利用率的同时，实现灵活调度。此外，由于每个阶段的初始激活值 x𝑙0 已在本地缓存，重计算过程与流水线通信依赖关系解耦。

图4｜mHC 的通信-计算重叠策略。
我们在 DualPipe 流水线调度基础上进行扩展，以应对 mHC 引入的额外开销。图中各块长度仅为示意，不代表实际耗时；(F)、(B)、(W) 分别表示前向、反向与权重梯度计算； F A \mathcal{F}^{\mathrm{A}} FA 与 F M \mathcal{F}^{\mathrm{M}} FM 分别对应 Attention 与 MLP 的内核。

5. 方法

5.1. 实验设置

我们通过语言模型预训练来验证所提出的方法，并对基线方法、HC以及我们提出的mHC进行了对比分析。借鉴DeepSeek-V3（Liu et al., 2024b）的MoE架构，我们训练了四种不同的模型变体以覆盖不同的评估场景。具体来说，HC和mHC的扩展率𝑛均设置为 4。我们主要关注一个27B模型，其训练数据集大小与其参数量成正比，这构成了我们系统级主要结果的研究对象。在此基础上，我们通过纳入按比例数据训练的较小3B和9B模型来分析计算扩展行为，这使我们能够观察不同计算量下的性能趋势。此外，为了专门研究token扩展行为，我们在一个固定的1万亿token语料库上训练了一个单独的3B模型。详细的模型配置和训练超参数见附录A.1。

5.2. 主要结果

我们首先考察27B模型的训练稳定性和收敛性。如图5a 所示，mHC有效缓解了在HC中观察到的训练不稳定性，相比基线最终损失降低了0.021。图5b 中的梯度范数分析进一步证实了这种稳定性的提升，mHC的表现显著优于HC，并保持了与基线相当的稳定态势。

表4 展示了在多样化基准测试（Bisk等人，2020；Cobbe等人，2021；Hendrycks等人，2020，2021；Joshi等人，2017；Zellers等人，2019）上的下游性能。mHC带来了全面的改进，始终优于基线，并在大多数任务上超过了HC。值得注意的是，与HC相比，mHC进一步增强了模型的推理能力，在BBH（Suzgun等人，2022）和DROP（Dua等人，2019）上分别带来了2.1%和2.3%的性能提升。

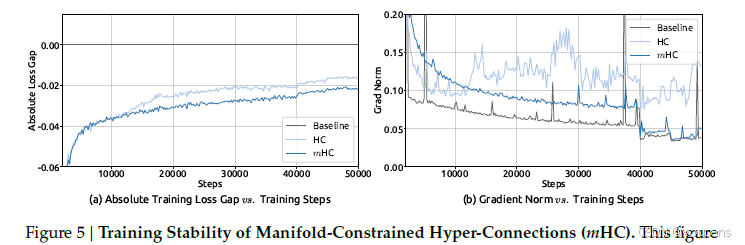
图5｜流形约束超连接（mHC）的训练稳定性。
(a) 相对于基线，mHC 与 HC 的绝对训练损失差距随训练步数变化；(b) 三种方法的梯度范数对比。所有实验均在 27B 模型上进行，结果显示 mHC 在损失与梯度两方面均显著优于 HC，且与基线相当。

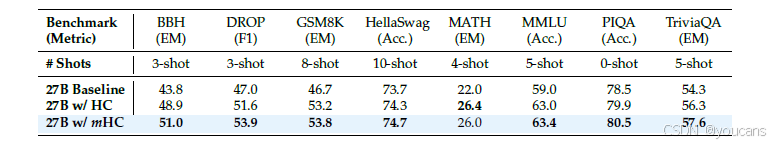
表4｜27B 模型系统级基准结果。
该表对比基线、HC 与 mHC 在 8 项下游任务上的零样本与少样本性能。mHC 在所有基准上均一致优于基线，并在绝大多数任务中超过 HC，验证了 mHC 在大规模预训练中的有效性。

5.3. 扩展实验

为了评估我们方法的可扩展性，我们报告了mHC在不同规模下相对于基线的损失改进。在图6（a）中，我们绘制了跨越3B、9B和27B参数的计算扩展曲线。该轨迹表明，即使在更高的计算预算下，性能优势也依然稳固，仅显示出微弱的衰减。此外，我们在图6（b）中考察了运行内的动态变化，展示了3B模型的token扩展曲线。总的来说，这些发现验证了mHC在大规模场景下的有效性。我们内部的大规模训练实验进一步证实了这一结论。

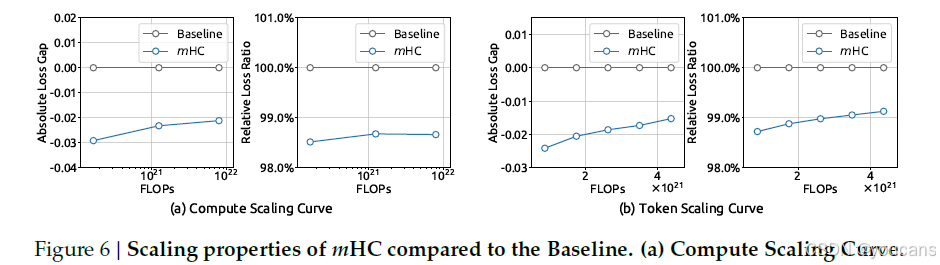
图6｜mHC 与基线的扩展特性。
(a) 计算扩展曲线：在 3B、9B、27B 三种参数规模下，mHC 相对基线的损失改善随计算预算变化；(b) Token 扩展曲线：3B 模型在 1T 令牌训练过程中的性能轨迹。两图均表明 mHC 的优势随规模放大而持续。

5.4. 稳定性分析

与图3 类似，图7展示了mHC的传播稳定性。理想情况下，单层映射应满足双随机约束，这意味着前向信号增益和后向梯度增益均应为1。然而，实际应用中采用Sinkhorn-Knopp算法时必须限制迭代次数以保证计算效率。在我们的设置中，我们使用20次迭代来获得近似解。因此，如图7(a)所示，后向梯度增益会略微偏离1。在图7(b)所示的复合情况下，偏差有所增加但仍保持有界，最大值约为1.6。值得注意的是，与HC中近3000的最大增益幅度相比，mHC将其显著降低了三个数量级。这些结果表明，与HC相比，mHC显著增强了传播稳定性，确保了前向信号和后向梯度的稳定流动。

此外，图8展示了代表性映射结果。我们观察到，对于HC而言，当最大增益值较大时，其他数值也往往非常显著，这表明所有传播路径均存在普遍不稳定性。相比之下，mHC始终能产生稳定的结果。

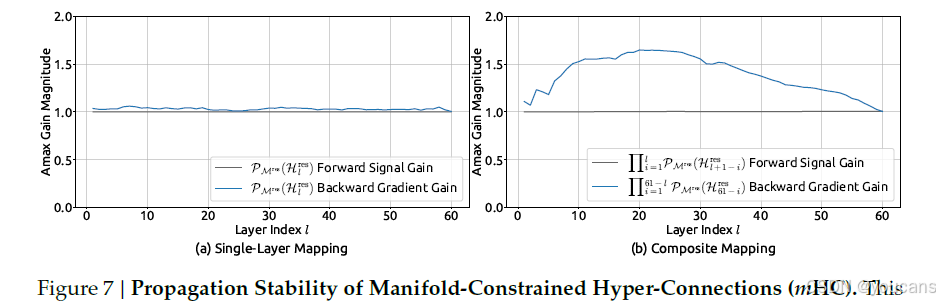
图7｜流形约束超连接（mHC）的传播稳定性。
(a) 单层映射 P M r e s ( H l r e s ) \mathrm{P}{\mathcal{M}^{\mathrm{res}}}(\mathcal{H}l^{\mathrm{res}}) PMres(Hlres) 的前向信号增益与反向梯度增益；(b) 复合映射 ∏ i = 1 L − l P M r e s ( H L − i r e s ) \prod{i=1}^{L-l}\mathrm{P}{\mathcal{M}^{\mathrm{res}}}(\mathcal{H}_{L-i}^{\mathrm{res}}) ∏i=1L−lPMres(HL−ires) 的对应增益。与 HC 近 3000 的峰值相比，mHC 的最大增益仅约 1.6，提升三个数量级。

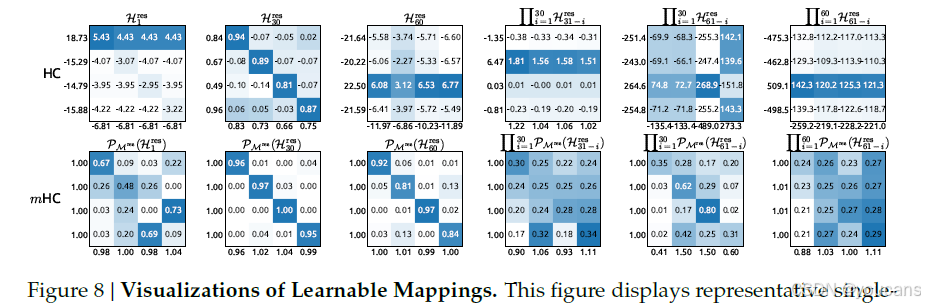
图8｜可学习映射可视化。
上行：HC 的代表性单层与复合映射；下行：mHC 的对应映射。每幅矩阵按序列内所有令牌平均。y 轴与 x 轴旁标注前行信号增益（行和）与反向梯度增益（列和）。HC 的高增益伴随整体数值放大，显示全局不稳定；mHC 的增益始终接近 1，表明传播稳定。

6. 结论与展望

本文研究发现，虽然如超连接（HC）方法所提出的那样扩展残差流宽度并实现连接多样化能够提升性能，但这些连接的无约束特性会导致信号发散。这种破坏损害了信号能量在层间的守恒性，从而引发训练不稳定并阻碍深度网络的可扩展性。为解决这些问题，我们引入了流形约束超连接（mHC）这一通用框架，它将残差连接空间投影到特定流形上。通过采用Sinkhorn-Knopp算法对残差映射施加双随机约束，mHC将信号传播转化为特征的凸组合。实证结果证实，mHC有效恢复了恒等映射特性，实现了稳定的大规模训练，并相比传统HC具有更优的可扩展性。重要的是，通过基础设施层面的高效优化，mHC以可忽略的计算开销实现了这些改进。

作为HC范式的广义扩展，mHC为未来研究开辟了多个前景广阔的路径。尽管本文利用双随机矩阵来确保稳定性，但该框架支持探索针对特定学习目标定制的多样化流形约束。我们预计，对不同几何约束的进一步研究可能催生新的方法，从而更好地权衡可塑性与稳定性。此外，我们希望mHC能重新激发学术界对宏观架构设计的兴趣。通过深化对拓扑结构如何影响优化和表征学习的理解，mHC将有助于解决当前局限，并可能为下一代基础架构的演进指明新方向。

附录：A.1. 详细模型规格与超参数

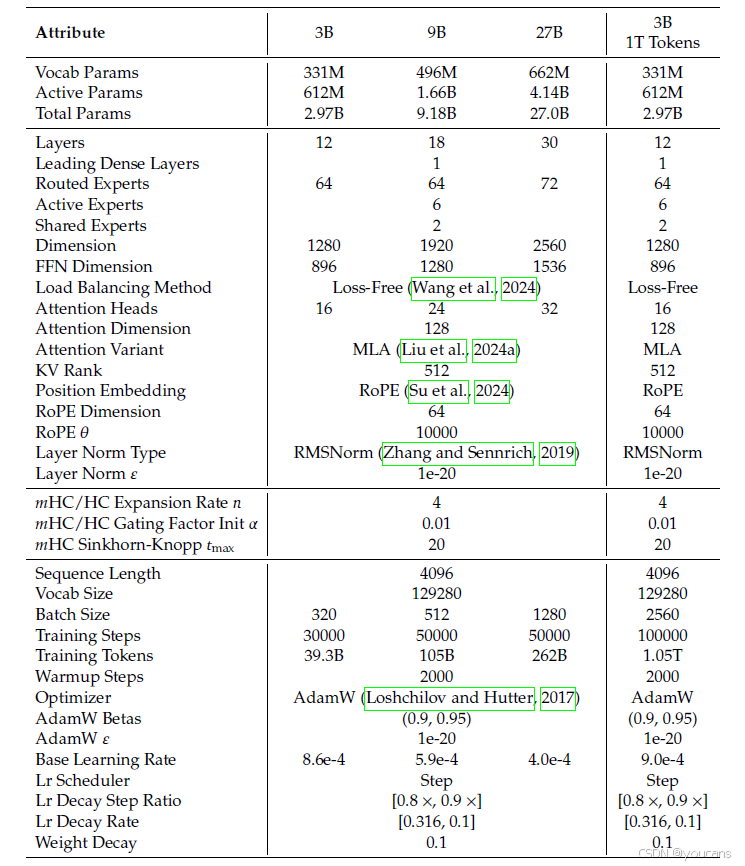
表5 | 详细模型规格与超参数。本表展示了基于DeepSeek-V3架构（Liu等人，2024b）的3B、9B和27B模型的架构配置。其中详细列出了mHC和HC的具体超参数，包括残差流扩展配置与Sinkhorn-Knopp算法设置，以及实验中采用的优化与训练方案。

参考文献

bash 复制代码

1. He, K., Zhang, X., Ren, S., & Sun, J. (2016a). Deep residual learning for image recognition. In *Proceedings of the IEEE conference on computer vision and pattern recognition* (pp. 770-778).
2. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. *Advances in neural information processing systems*, 30.
3. Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J. D., Dhariwal, P., ... & Amodei, D. (2020). Language models are few-shot learners. *Advances in neural information processing systems*, 33, 1877-1901.
4. Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M., Chen, D., ... & Stoyanov, V. (2019). RoBERTa: A robustly optimized BERT pretraining approach. *arXiv preprint arXiv:1907.11692*.
5. Touvron, H., Lavril, T., Izacard, G., Martinet, X., Lachaux, M. A., Lacroix, T., ... & Jégou, H. (2023). LLaMA: Open and efficient foundation language models. *arXiv preprint arXiv:2302.13971*.
6. He, K., Zhang, X., Ren, S., & Sun, J. (2016b). Identity mappings in deep residual networks. In *European conference on computer vision* (pp. 630-645). Springer.
7. Zhu, Z., Huang, H., Zeng, Y., Mao, Y., Wu, B., Min, Q., ... & Zhou, X. (2024). Hyper-connections. *arXiv preprint arXiv:2311.17554*.
8. Sinkhorn, R., & Knopp, P. (1967). Concerning nonnegative matrices and doubly stochastic matrices. *Pacific Journal of Mathematics*, 21(2), 343-348.
9. Wang, L., Cheng, Y., Shi, Y., Tang, Z., Mo, Z., Xie, W., ... & Yang, F. (2025). TileLang: A composable tiled programming model for AI systems. *arXiv preprint arXiv:2504.17577*.
10. Liu, A., Feng, B., Xue, B., Wang, B., Wu, B., Lu, C., ... & Ruan, C. (2024b). DeepSeek-V3 technical report. *arXiv preprint arXiv:2412.19437*.
11. Chollet, F. (2017). Xception: Deep learning with depthwise separable convolutions. In *Proceedings of the IEEE conference on computer vision and pattern recognition* (pp. 1251-1258).
12. Xie, S., Girshick, R., Dollár, P., Tu, Z., & He, K. (2017). Aggregated residual transformations for deep neural networks. In *Proceedings of the IEEE conference on computer vision and pattern recognition* (pp. 1492-1500).
13. Shazeer, N. (2019). Fast transformer decoding: One write-head is all you need. *arXiv preprint arXiv:1911.02150*.
14. Ainslie, J., Lee-Thorp, J., de Jong, M., Zemlyanskiy, Y., Lebrón, F., & Sanghai, S. (2023). GQA: Training generalized multi-query transformer models from multi-head checkpoints. *arXiv preprint arXiv:2305.13245*.
15. Liu, A., Feng, B., Xue, B., Wang, B., Wu, B., Lu, C., ... & Zhang, C. (2024a). DeepSeek-V2: A strong, economical, and efficient mixture-of-experts language model. *arXiv preprint arXiv:2405.04434*.
16. Fedus, W., Zoph, B., & Shazeer, N. (2022). Switch transformers: Scaling to trillion parameter models with simple and efficient sparsity. *Journal of Machine Learning Research*, 23(120), 1-39.
17. Lepikhin, D., Lee, H., Xu, Y., Chen, D., Firat, O., Huang, Y., ... & Chen, Z. (2020). GShard: Scaling giant models with conditional computation and automatic sharding. *arXiv preprint arXiv:2006.16668*.
18. Shazeer, N., Mirhoseini, A., Maziarz, K., Davis, A., Le, Q., Hinton, G., & Dean, J. (2017). Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. *arXiv preprint arXiv:1701.06538*.
19. Srivastava, R. K., Greff, K., & Schmidhuber, J. (2015). Training very deep networks. In *Advances in neural information processing systems* (Vol. 28).
20. Huang, G., Liu, Z., Van Der Maaten, L., & Weinberger, K. Q. (2017). Densely connected convolutional networks. In *Proceedings of the IEEE conference on computer vision and pattern recognition* (pp. 4700-4708).
21. Larsson, G., Maire, M., & Shakhnarovich, G. (2016). FractalNet: Ultra-deep neural networks without residuals. *arXiv preprint arXiv:1605.07648*.
22. Yu, F., Wang, D., Shelhamer, E., & Darrell, T. (2018). Deep layer aggregation. In *Proceedings of the IEEE conference on computer vision and pattern recognition* (pp. 2403-2412).
23. Chai, Y., Jin, S., & Hou, X. (2020). Highway transformer: Self-gating enhanced self-attentive networks. In *Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics* (pp. 6887-6900).
24. Fang, Y., Cai, Y., Chen, J., Zhao, J., Tian, G., & Li, G. (2023). Cross-layer retrospective retrieving via layer attention. In *The Eleventh International Conference on Learning Representations*.
25. Heddes, M., Javanmard, A., Axiotis, K., Fu, G., Bateni, M., & Mirrokni, V. (2025). DeepCrossAttention: Supercharging transformer residual connections. In *Forty-second International Conference on Machine Learning*.
26. Mak, B., & Flanigan, J. (2025). Residual matrix transformers: Scaling the size of the residual stream. *arXiv preprint arXiv:2506.22696*.
27. Menghani, G., Kumar, R., & Kumar, S. (2025). LAurel: Learned augmented residual layer. In *Forty-second International Conference on Machine Learning*.
28. Pagliardini, M., Mohtashami, A., Fleuret, F., & Jaggi, M. (2024). DenseFormer: Enhancing information flow in transformers via depth weighted averaging. In *The Thirty-eighth Annual Conference on Neural Information Processing Systems*.
29. Xiao, D., Meng, Q., Li, S., & Yuan, X. (2025). MUDDFormer: Breaking residual bottlenecks in transformers via multiway dynamic dense connections. *arXiv preprint arXiv:2502.12170*.
30. Xie, S., Zhang, H., Guo, J., Tan, J., Bian, J., Awadalla, H. H., ... & Yan, R. (2023). ResiDual: Transformer with dual residual connections. *arXiv preprint arXiv:2304.14802*.
31. Zhang, B., & Sennrich, R. (2019). Root mean square layer normalization. *Advances in Neural Information Processing Systems*, 32.
32. Su, J., Ahmed, M., Lu, Y., Pan, S., Bo, W., & Liu, Y. (2024). RoFormer: Enhanced transformer with rotary position embedding. *Neurocomputing*, 568, 127063.
33. Loshchilov, I., & Hutter, F. (2017). Decoupled weight decay regularization. *arXiv preprint arXiv:1711.05101*.
34. Dao, T., Fu, D. Y., Ermon, S., Rudra, A., & Ré, C. (2022). FlashAttention: Fast and memory-efficient exact attention with IO-awareness. In *Advances in Neural Information Processing Systems*.
35. Qi, P., Wan, X., Huang, G., & Lin, M. (2024). Zero bubble (almost) pipeline parallelism. In *The Twelfth International Conference on Learning Representations*.
36. Bisk, Y., Zellers, R., Gao, J., & Choi, Y. (2020). PIQA: Reasoning about physical commonsense in natural language. In *Proceedings of the AAAI Conference on Artificial Intelligence* (Vol. 34, No. 05, pp. 7432-7439).
37. Cobbe, K., Kosaraju, V., Bavarian, M., Chen, M., Jun, H., Kaiser, L., ... & Nakano, R. (2021). Training verifiers to solve math word problems. *arXiv preprint arXiv:2110.14168*.
38. Hendrycks, D., Burns, C., Basart, S., Zou, A., Mazeika, M., Song, D., & Steinhardt, J. (2020). Measuring massive multitask language understanding. *arXiv preprint arXiv:2009.03300*.
39. Hendrycks, D., Burns, C., Kadavath, S., Arora, A., Basart, S., Tang, E., ... & Steinhardt, J. (2021). Measuring mathematical problem solving with the MATH dataset. *arXiv preprint arXiv:2103.03874*.
40. Joshi, M., Choi, E., Weld, D. S., & Zettlemoyer, L. (2017). TriviaQA: A large scale distantly supervised challenge dataset for reading comprehension. In *Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics* (Vol. 1, pp. 1601-1611).
41. Zellers, R., Holtzman, A., Bisk, Y., Farhadi, A., & Choi, Y. (2019). HellaSwag: Can a machine really finish your sentence? In *Proceedings of the 57th Conference of the Association for Computational Linguistics* (pp. 4791-4800).
42. Suzgun, M., Scales, N., Schärli, N., Gehrmann, S., Tay, Y., Chung, H. W., ... & Zhou, D. (2022). Challenging BIG-Bench tasks and whether chain-of-thought can solve them. *arXiv preprint arXiv:2210.09261*.
43. Dua, D., Wang, Y., Dasigi, P., Stanovsky, G., Singh, S., & Gardner, M. (2019). DROP: A reading comprehension benchmark requiring discrete reasoning over paragraphs. In *Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies* (Vol. 1, pp. 2368-2378).
44. Wang, L., Gao, H., Zhao, C., Sun, X., & Dai, D. (2024). Auxiliary-loss-free load balancing strategy for mixture-of-experts. *arXiv preprint arXiv:2408.15664*.

本文由 youcans@xidian 对论文 mHC: Manifold-Constrained Hyper-Connections

进行摘编和翻译，只供研究学习使用。

论文引用：

Z. Xie, Y. et al. and W. Liang, "mHC: Manifold-constrained hyper-connections," arXiv preprint arXiv:2512.24880, Dec. 2025. doi: 10.48550/arXiv.2512.24880.

youcans@xidian 作品 ，转载必须标注原文链接：
【DeepSeek论文精读】14. mHC：流形约束超连接

Created：2026-01