贪心（四）——拟阵算法设计与分析国科大

本文涉及的算法内容不多，只围绕一个问题------贪心算法在是什么时候可以得到最优解（或者近似解）进行讨论。

贪心策略解决的是一类子集优化问题，其通用框架为：

输入：有限对象集合N，约束子集族（规定哪些子集S是 "合法" 的），集合函数f(S)（衡量子集S的价值）。
目标：找到合法子集，使得f(S)最大化，即。
一般难度：该问题通常是难解的 （需枚举所有合法子集才能保证找到最优解）；但当或f(S)满足特定性质时，贪心策略可高效得到最优 / 近似解。

简单来说，假设你有一堆东西，想从中挑一部分，但挑的这堆得符合某些规矩（比如不能超重、不能有冲突）；同时，你希望挑出来的这堆东西，能让某个 "好处"（比如总价值、总效率）尽可能大。但这个问题一般情况下特别难办 ------ 因为要把所有 "符合规矩的挑法" 都试一遍，才能确定哪个是最好的，东西多了根本试不完。不过在一些特殊场景里，不用这么费劲：可以用 "贪心策略"（每次只挑当前看起来最划算的那个，而且保证不违反规矩），就能直接选出最好的那组，或者至少选出一组很不错的结果。

而符合拟阵结构的场景，天然居然最优贪心的性质。

贪心算法什么时候能得到最优解/近似解？

（1）拟阵（Matroid）：贪心能得到全局最优解

适用条件：
- 集合函数f(S)是线性函数 （如，即子集价值为元素权重之和）；
- 约束对应独立子集族（满足两个核心性质：①遗传性：独立子集的子集仍是独立子集；②交换性：若两个独立子集大小不同，可从大的子集中选元素扩展小的子集）。
效果：贪心策略（每次选 "当前最优" 的元素，且保持子集合法）能生成全局最优解。
典型例子：最小生成树（Kruskal/Prim 算法）、部分背包问题（物品可分割）。

（2）次模函数（Submodular functions）：贪心能得到近似最优解

适用条件：
- 集合函数f(S)是次模函数 ，核心性质是 "边际收益递减 "：向更大的集合添加元素时，新元素的 "边际价值" 不增（如，当时）。
效果：贪心策略无法保证全局最优，但能生成可证明的近似最优解（近似比有理论上界）。
典型例子：资源分配、特征选择、最大覆盖问题等。

拟阵性质

拟阵（Matroid）是一种抽象的数学结构，是贪心算法能得到全局最优解的核心理论基础之一。它的数学定义是：

拟阵是一个二元组，其中：

E 是一个有限集合（称为 "元素集"）；
是 E 的子集族（称为 "独立集族"），且满足以下 3 条公理：
- 公理 1（空集合法） ：空集是独立集，即；
- 公理 2（遗传性 / 向下封闭） ：若一个子集是独立集，它的任意子集也是独立集。即若且，则；
- 公理 3（交换性 / 扩展性质） ：若两个独立集的大小不同，小的独立集可以通过添加大的独立集中的元素来扩展。即若且 |A| < |B|，则存在元素，使得。

用之前的区间调度问题举个例子：

假设你这个学期有 5 门课可以选，每门课对应 "上课时间" 和 "学分"（学分相当于 "收益"），约束是：选的课程不能有时间重叠（这是 "合法组合" 的规则）。

课程列表：

课 A：周一 1-2 节，2 学分
课 B：周一 3-4 节，3 学分
课 C：周二 1-2 节，2 学分
课 D：周二 3-4 节，3 学分
课 E：周一 1-2 节，4 学分（和课 A 时间冲突）

拟阵的核心是 "合法组合的规则满足两个特点"，对应这个场景：

遗传性（选的课少了，肯定也合法）：比如你选了 "课 B + 课 C"（周一 3-4 + 周二 1-2，无冲突），那只选 "课 B"（或者只选 "课 C"）也一定没冲突 ------ 符合 "合法组合的子集也合法"。
扩展性质（小的合法组合，能加别人的课变大）：比如你只选了 "课 A"（2 学分），而别人选了 "课 B + 课 D"（6 学分，无冲突），那别人的课里肯定有一门能加到你的 "课 A" 里还不冲突（比如加课 D，课 A 和课 D 时间不重叠）------ 符合 "小的合法组合可以用大组合里的元素扩展"。

而拟阵的 "贪心策略能拿最优"，对应这个场景就是：你想凑 "最高学分"，可以用 "每次选当前学分最高、且不冲突的课"：

先选学分最高的课 E（4 学分，周一 1-2）；
再选剩下课里学分最高、且不冲突的课 D（3 学分，周二 3-4）；
最后选剩下课里不冲突的课 C（2 学分，周二 1-2）。

最终选了 "E+D+C"，总学分 9------ 这就是拟阵保证的 "贪心选当前最好的，结果就是全局最好的"，关于拟阵为什么能做到这一点，会在下面进行证明

线性代数中的常见任务------极大线性无关集

现在给定一组向量，要求找到其中的极大线性无关集 ------ 即集合内向量彼此线性无关，且无法再添加任何剩余向量（否则会出现线性相关）。如图所示，最终的极大线性无关集是，在线性代数中，这个问题非常简单，而其对应了拟阵中一种非常重要的分类------向量拟阵。

极大无关集的贪心算法

步骤为：

初始化空集合 S（空集天然线性无关）；
遍历每个向量 v：
- 若仍保持线性无关，则将 v 加入 S；
返回最终的 S（即极大线性无关集）。

下面证明极大无关集满足拟阵性质

线性无关集对应的是向量拟阵（拟阵的一种），因此满足拟阵的两大关键性质：

遗传性：若 B 是线性无关集，A 是 B 的子集，则 A 也一定是线性无关集。（线性代数中，无关向量组的任意子集必然无关，不会出现 "子集相关而原集合无关" 的情况）。
扩展性质（拟阵的交换性） ：若 A、B 都是线性无关集，且 |A| < |B|，则 B 中存在一个向量 v，使得仍为线性无关集。
示例验证：设（大小 3）、（大小 4），由于 |A| < |B|，从 B 中选取加入 A，得到的仍保持线性无关。

证明拟阵具有贪心选择性质

1. 定理内容

在拟阵M中，若v是权重最大 且单元素集合{v}是独立集的向量，则存在包含v的最优独立集（即权重和最大的独立集）。

2. 证明（反证法）

假设存在最优独立集B，但；
构造新集合A：
1. 初始令A = {v}（因{v}是独立集）；
2. 利用拟阵的扩展性质 （交换性）：反复从B中选元素加入A，直到|A| = |B|（此时，v'是从B中替换的元素）；
由于v是权重最大的元素，故，因此A的权重和；
这与 "B是最优集" 矛盾，故必存在包含v的最优独立集。

通用贪心算法

凡是具有拟阵性质的常见，都有通用的贪心算法

复制代码

MATROIDGREEDY(M, W)
1: S = ∅;  // 初始化空独立集
2: 将所有向量按权重降序排序;  // 局部最优的选择依据
3: 遍历每个向量v:
4:   若 S ∪ {v} 仍是独立集:
5:     S = S ∪ {v};
6: 返回 S;

拟阵的起源*

起源1

拟阵的概念源于对 "向量线性无关集" 性质的抽象，该类集合满足拟阵的两大核心性质：

遗传性 ：若B是线性无关向量集，，则A也一定是线性无关向量集（无关集的子集必然无关）。
扩展性质 ：若A、B都是线性无关向量集且|A| < |B|，则B中存在向量v，使得仍线性无关。

示例验证 ：以向量集为例，（大小 3）、（大小 4），从B中选加入A，得到的仍线性无关。

起源2

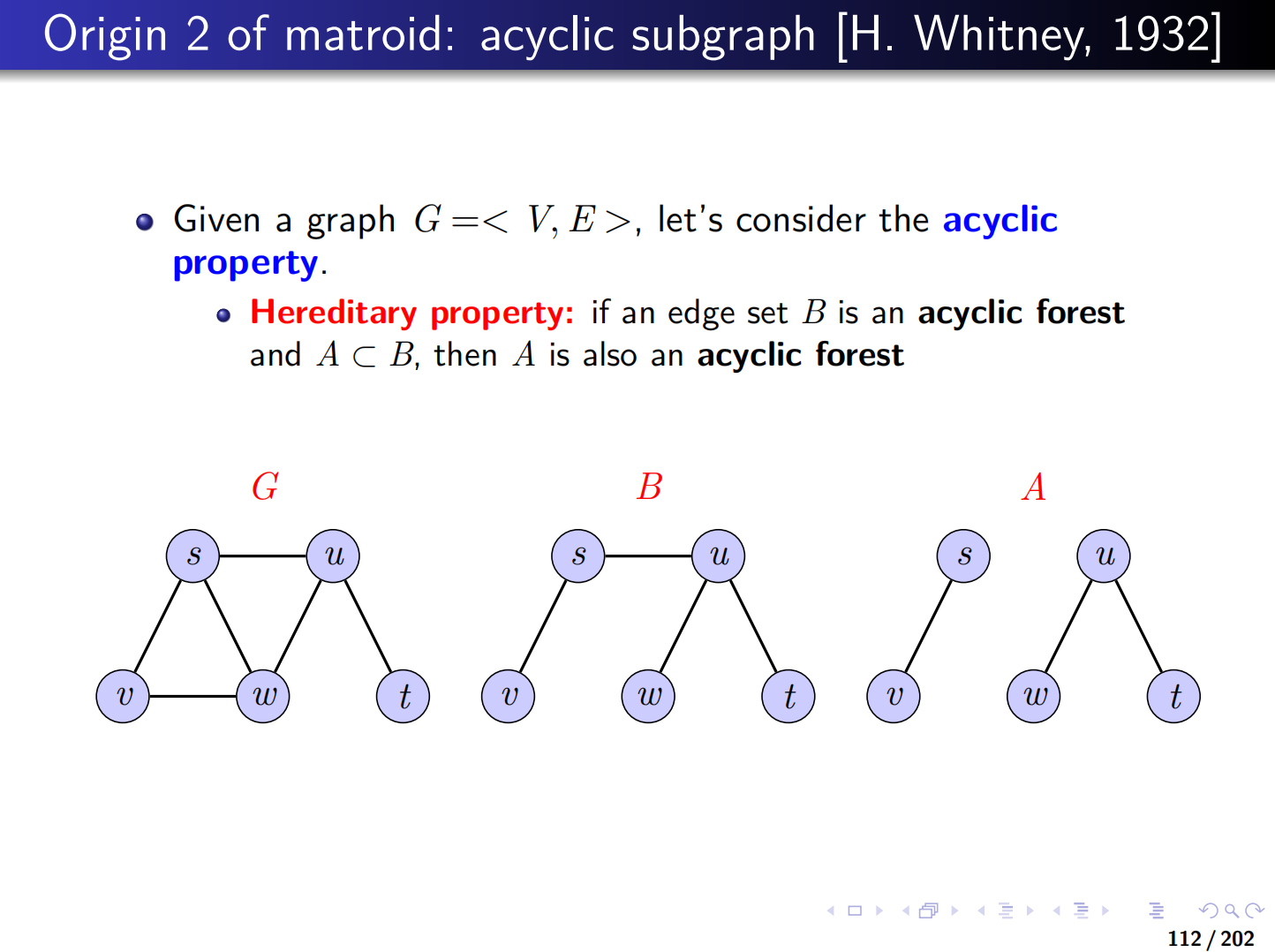
拟阵在图论中的体现是 "无环边集（森林）"，这类边集同样满足拟阵的核心性质：

遗传性 ：若B是无环边集（森林），，则A也一定是无环边集（无环边集的子集不会产生环）。
- 示例：图G的无环边集B（森林）的子集A，仍是无环的森林。
扩展性质 ：若A、B都是无环边集且|A| < |B|，则B中存在边e，使得仍无环。
- 推导逻辑：边数越少的森林，连通分量（树）越多；B中必然存在一条边，能连接A的两个不同连通分量，加入后不会形成环。
- 关联矩阵解释：图的关联矩阵中，边对应的列向量线性相关，等价于这些边构成环 ------ 因此 "添加不形成环的边" 对应 "添加不导致线性相关的列向量"，与向量拟阵的性质一致。

贪心（四）——拟阵 算法设计与分析 国科大