[机器学习-从入门到入土] 神经网络

[机器学习-从入门到入土] 神经网络

个人导航

知乎：https://www.zhihu.com/people/byzh_rc

CSDN：https://blog.csdn.net/qq_54636039

注：本文仅对所述内容做了框架性引导，具体细节可查询其余相关资料or源码

参考文章：各方资料

文章目录

• [[机器学习-从入门到入土] 神经网络](#[机器学习-从入门到入土] 神经网络)
• 个人导航
• 符号说明
• • • • [权重矩阵 Θ ( l ) \Theta^{(l)} Θ(l)](#权重矩阵 Θ ( l ) \Theta^{(l)} Θ(l))
      • [误差项 δ ( l ) \delta^{(l)} δ(l)](#误差项 δ ( l ) \delta^{(l)} δ(l))
      • [单样本梯度矩阵 δ k ( l + 1 ) ( a k ( l ) ) T \delta_{k}^{(l+1)} \left(a_{k}^{(l)}\right)^{T} δk(l+1)(ak(l))T](#单样本梯度矩阵 δ k ( l + 1 ) ( a k ( l ) ) T \delta_{k}^{(l+1)} \left(a_{k}^{(l)}\right){T} δk(l+1)(ak(l))T)
      • [批量梯度累加矩阵 Δ ( l ) \Delta^{(l)} Δ(l)](#批量梯度累加矩阵 Δ ( l ) \Delta^{(l)} Δ(l))
      • [总梯度（代价函数梯度） ∂ ∂ Θ i j ( l ) J ( Θ ) \frac{\partial}{\partial \Theta_{ij}^{(l)}} J(\Theta) ∂Θij(l)∂J(Θ)](#总梯度（代价函数梯度） ∂ ∂ Θ i j ( l ) J ( Θ ) \frac{\partial}{\partial \Theta_{ij}^{(l)}} J(\Theta) ∂Θij(l)∂J(Θ))
• [激活函数（Activation Function）](#激活函数（Activation Function）)
• • • • Sigmoid
      • ReLU
• [损失函数 E E E（单样本）](#损失函数 E E E（单样本）)
• • • • 1.均方误差（MSE）
      • [2.交叉熵（Binary Cross-Entropy）](#2.交叉熵（Binary Cross-Entropy）)
• [代价函数 J J J（全样本）](#代价函数 J J J（全样本）)
• [误差项 δ \delta δ（核心）](#误差项 δ \delta δ（核心）)
• [输出层误差项 δ ( L ) \delta^{(L)} δ(L)](#输出层误差项 δ ( L ) \delta^{(L)} δ(L))
• • • • [Sigmoid + MSE](#Sigmoid + MSE)
      • [Sigmoid + Binary Cross-Entropy](#Sigmoid + Binary Cross-Entropy)
      • [Softmax + Categorical Cross-Entropy](#Softmax + Categorical Cross-Entropy)
• [隐藏层误差项 δ ( ) \delta^{()} δ()](#隐藏层误差项 δ ( ) \delta^{()} δ())
• [批量梯度累加 Δ ( l ) \Delta^{(l)} Δ(l)](#批量梯度累加 Δ ( l ) \Delta^{(l)} Δ(l))
• 总梯度（用于更新）
• [是批量梯度累加 Δ ( l ) \Delta^{(l)} Δ(l)的平均 $$ \frac{\partial}{\partial \Theta^{(l)}}J(\Theta)](#是批量梯度累加 Δ ( l ) \Delta^{(l)} Δ(l)的平均 $$ \frac{\partial}{\partial \Theta^{(l)}}J(\Theta))
• [前向传播（Forward Propagation）](#前向传播（Forward Propagation）)
• 反向传播（Backpropagation）
• 梯度下降更新
• 总结（反向传播主线）

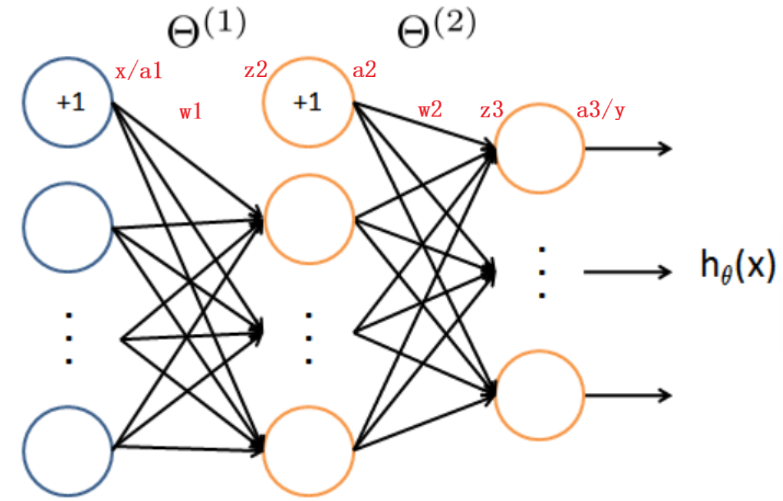
符号说明

m m m：样本数
k k k：神经元编号 / 输出维度索引

权重矩阵 Θ ( l ) \Theta^{(l)} Θ(l)

Θ ( l ) \Theta^{(l)} Θ(l) 表示 第 l l l 层 → 第 l + 1 l+1 l+1 层的权重矩阵

• 包含该层的 权重 + bias
• 行：第 l + 1 l+1 l+1 层神经元
• 列： 1 + 1+ 1+ 第 l l l 层神经元数（首列为 bias）

维度：(下一层神经元数, 1+当前层神经元数)

Θ ( l ) ∈ R ( next ,   1 + self ) \Theta^{(l)} \in \mathbb{R}^{(\text{next},\,1+\text{self})} Θ(l)∈R(next,1+self)

误差项 δ ( l ) \delta^{(l)} δ(l)

δ ( l ) \delta^{(l)} δ(l) 表示 第 l l l 层神经元的误差项

• 本质： ∂ E ∂ z ( l ) \displaystyle \frac{\partial E}{\partial z^{(l)}} ∂z(l)∂E
• 用于将误差从输出层反向传播

特殊记号：

• δ ( L ) \delta^{(L)} δ(L)：输出层误差（ L L L 为网络总层数）

单样本梯度矩阵 δ k ( l + 1 ) ( a k ( l ) ) T \delta_{k}^{(l+1)} \left(a_{k}^{(l)}\right)^{T} δk(l+1)(ak(l))T

δ k ( l + 1 ) ( a k ( l ) ) T \delta_{k}^{(l+1)} \left(a_{k}^{(l)}\right)^{T} δk(l+1)(ak(l))T

• 表示 单个样本 对 Θ ( l ) \Theta^{(l)} Θ(l) 的梯度
• 外积形式
• 维度与 Θ ( l ) \Theta^{(l)} Θ(l) 相同

批量梯度累加矩阵 Δ ( l ) \Delta^{(l)} Δ(l)

Δ ( l ) \Delta^{(l)} Δ(l) 表示 第 l l l 层在一个 batch（ m m m 个样本）上的梯度累加

Δ ( l ) ∈ R ( next ,   1 + self ) \Delta^{(l)} \in \mathbb{R}^{(\text{next},\,1+\text{self})} Δ(l)∈R(next,1+self)

总梯度（代价函数梯度） ∂ ∂ Θ i j ( l ) J ( Θ ) \frac{\partial}{\partial \Theta_{ij}^{(l)}} J(\Theta) ∂Θij(l)∂J(Θ)

∂ ∂ Θ i j ( l ) J ( Θ ) \frac{\partial}{\partial \Theta_{ij}^{(l)}} J(\Theta) ∂Θij(l)∂J(Θ)

• 维度与 Θ ( l ) \Theta^{(l)} Θ(l) 相同
• 是 Δ ( l ) \Delta^{(l)} Δ(l) 的平均

符号	形状	解释
a ( l ) a^{(l)} a(l)	( self , 1 ) (\text{self},1) (self,1)	第 l l l 层神经元的激活输出向量（不含 bias）
a ~ ( l ) \tilde a^{(l)} a~(l)	( 1 + self , 1 ) (1+\text{self},1) (1+self,1)	第 l l l 层激活向量补 1 后的输入（首元素为 bias）
z ( l + 1 ) z^{(l+1)} z(l+1)	( next , 1 ) (\text{next},1) (next,1)	第 l + 1 l+1 l+1 层的加权输入（线性部分）
Θ ( l ) \Theta^{(l)} Θ(l)	( next , 1 + self ) (\text{next},1+\text{self}) (next,1+self)	第 l l l 层 → 第 l + 1 l+1 l+1 层的权重矩阵（含 bias）
δ ( l ) \delta^{(l)} δ(l)	( self , 1 ) (\text{self},1) (self,1)	第 l l l 层神经元的误差项 ， ∂ E ∂ z ( l ) \displaystyle \frac{\partial E}{\partial z^{(l)}} ∂z(l)∂E
δ ( l + 1 ) ( a ~ ( l ) ) T \delta^{(l+1)}(\tilde a^{(l)})^T δ(l+1)(a~(l))T	( next , 1 + self ) (\text{next},1+\text{self}) (next,1+self)	单样本 对 Θ ( l ) \Theta^{(l)} Θ(l) 的梯度（外积）
Δ ( l ) \Delta^{(l)} Δ(l)	( next , 1 + self ) (\text{next},1+\text{self}) (next,1+self)	batch 内 m m m 个样本的梯度累加矩阵
∂ ∂ Θ ( l ) J ( Θ ) \dfrac{\partial}{\partial \Theta^{(l)}}J(\Theta) ∂Θ(l)∂J(Θ)	( next , 1 + self ) (\text{next},1+\text{self}) (next,1+self)	代价函数对权重的总梯度 （ 1 m Δ ( l ) \frac{1}{m}\Delta^{(l)} m1Δ(l)）

激活函数（Activation Function）

Sigmoid

定义：
g ( z ) = 1 1 + exp ⁡ ( − z ) g(z)=\frac{1}{1+\exp(-z)} g(z)=1+exp(−z)1

梯度：
g ′ ( z ) = g ( z ) ( 1 − g ( z ) ) g'(z)=g(z)(1-g(z)) g′(z)=g(z)(1−g(z))

若 a = g ( z ) a=g(z) a=g(z)：
g ′ ( z ) = a ( 1 − a ) g'(z)=a(1-a) g′(z)=a(1−a)

ReLU

定义：
ReLU ( z ) = max ⁡ ( 0 , z ) \text{ReLU}(z)=\max(0,z) ReLU(z)=max(0,z)

梯度：
ReLU ′ ( z ) = { 1 , z > 0 0 , z ≤ 0 \text{ReLU}'(z)= \begin{cases} 1,&z>0\\ 0,&z\le0 \end{cases} ReLU′(z)={1,0,z>0z≤0

损失函数 E E E（单样本）

单个样本的误差，用于衡量模型输出与目标之间的差异

1.均方误差（MSE）

E = 1 2 ( t − y ) 2 E=\frac{1}{2}(t-y)^2 E=21(t−y)2

2.交叉熵（Binary Cross-Entropy）

E = − [ t log ⁡ y + ( 1 − t ) log ⁡ ( 1 − y ) ] E=-[t\log y+(1-t)\log(1-y)] E=−[tlogy+(1−t)log(1−y)]

代价函数 J J J（全样本）

整个训练集的平均损失：
J ( Θ ) = 1 m ∑ i = 1 m E ( i ) J(\Theta)=\frac{1}{m}\sum_{i=1}^{m}E^{(i)} J(Θ)=m1i=1∑mE(i)

误差项 δ \delta δ（核心）

误差项是 损失函数对加权输入 z z z 的偏导数 ：
δ ( l ) = ∂ E ∂ z ( l ) \delta^{(l)}=\frac{\partial E}{\partial z^{(l)}} δ(l)=∂z(l)∂E

输出层误差项 δ ( L ) \delta^{(L)} δ(L)

假设：
a ( L ) = g ( z ( L ) ) a^{(L)}=g(z^{(L)}) a(L)=g(z(L))

定义：
δ ( L ) = ∂ E ∂ a ( L ) ⊙ g ′ ( z ( L ) ) \delta^{(L)}=\frac{\partial E}{\partial a^{(L)}} \odot g'(z^{(L)}) δ(L)=∂a(L)∂E⊙g′(z(L))

Sigmoid + MSE

E = 1 2 ∑ k ( a k − y k ) 2 E=\frac{1}{2}\sum_k(a_k-y_k)^2 E=21k∑(ak−yk)2

δ k = ( a k − y k ) a k ( 1 − a k ) \delta_k=(a_k-y_k)a_k(1-a_k) δk=(ak−yk)ak(1−ak)

δ = ( a − y ) ⊙ ( a ⊙ ( 1 − a ) ) \delta=(a-y)\odot(a\odot(1-a)) δ=(a−y)⊙(a⊙(1−a))

Sigmoid + Binary Cross-Entropy

E = − [ y log ⁡ a + ( 1 − y ) log ⁡ ( 1 − a ) ] E=-[y\log a+(1-y)\log(1-a)] E=−[yloga+(1−y)log(1−a)]

δ = a − y \delta=a-y δ=a−y

Softmax + Categorical Cross-Entropy

E = − ∑ k y k log ⁡ a k E=-\sum_k y_k\log a_k E=−k∑yklogak

δ = a − y \delta=a-y δ=a−y

隐藏层误差项 δ ( ) \delta^{()} δ()

递推公式（反向传播核心）：

\\begin{align} \\delta\^{(L-1)} \&= \\frac{\\partial E}{\\partial a^{(L-1)}}⊙g'(z^{(L-1)}) \\ \&=(\\frac{\\partial E}{\\partial z\^{(L)}} \\cdot \\frac{\\partial z\^{(L)}}{\\partial a^{(L-1)}})⊙g'(z^{(L-1)}) \\ \&= \\delta\^{(L)} \\Theta\^{(L-1)} ⊙ g\^{\\prime} (z\^{(L-1)}) \\ \\end{align}

说明：

• 先通过权重矩阵传播误差
• 再乘以激活函数梯度

批量梯度累加 Δ ( l ) \Delta^{(l)} Δ(l)

单样本梯度：
δ ( l + 1 ) ( a ( l ) ) T \delta^{(l+1)}(a^{(l)})^T δ(l+1)(a(l))T

批量累加：
Δ ( l ) = ∑ i = 1 m δ i ( l + 1 ) ( a i ( l ) ) T \Delta^{(l)}=\sum_{i=1}^m \delta_i^{(l+1)}(a_i^{(l)})^T Δ(l)=i=1∑mδi(l+1)(ai(l))T

总梯度（用于更新）

是批量梯度累加 Δ ( l ) \Delta^{(l)} Δ(l)的平均

\\frac{\\partial}{\\partial \\Theta\^{(l)}}J(\\Theta) \\frac{1}{m}\\Delta\^{(l)}

前向传播（Forward Propagation）

每一层输入补 1（bias）：
a ~ ( l ) = [ 1 a ( l ) ] \tilde a^{(l)}= \begin{bmatrix} 1\\ a^{(l)} \end{bmatrix} a~(l)=[1a(l)]

线性变换：
z ( l + 1 ) = Θ ( l ) a ~ ( l ) z^{(l+1)}=\Theta^{(l)}\tilde a^{(l)} z(l+1)=Θ(l)a~(l)

非线性激活：
a ( l + 1 ) = g ( z ( l + 1 ) ) a^{(l+1)}=g(z^{(l+1)}) a(l+1)=g(z(l+1))

反向传播（Backpropagation）

假设三层全连接网络，Sigmoid + BCE

输出层：
δ ( 3 ) = a ( 3 ) − y \delta^{(3)}=a^{(3)}-y δ(3)=a(3)−y

隐藏层：
δ ( 2 ) = ( Θ ( 2 ) ) T δ ( 3 ) ⊙ g ′ ( z ( 2 ) ) \delta^{(2)}=(\Theta^{(2)})^T\delta^{(3)}\odot g'(z^{(2)}) δ(2)=(Θ(2))Tδ(3)⊙g′(z(2))

梯度下降更新

学习率 α \alpha α：

Θ ( l ) ← Θ ( l ) − α 1 m Δ ( l ) \Theta^{(l)} \leftarrow \Theta^{(l)}-\alpha\frac{1}{m}\Delta^{(l)} Θ(l)←Θ(l)−αm1Δ(l)

总结（反向传播主线）

前向传播：
a → z → a a \rightarrow z \rightarrow a a→z→a

反向传播：
δ ( L ) → δ ( L − 1 ) → ⋯ \delta^{(L)} \rightarrow \delta^{(L-1)} \rightarrow \cdots δ(L)→δ(L−1)→⋯

梯度构造：
δ ( l + 1 ) ( a ( l ) ) T \delta^{(l+1)}(a^{(l)})^T δ(l+1)(a(l))T