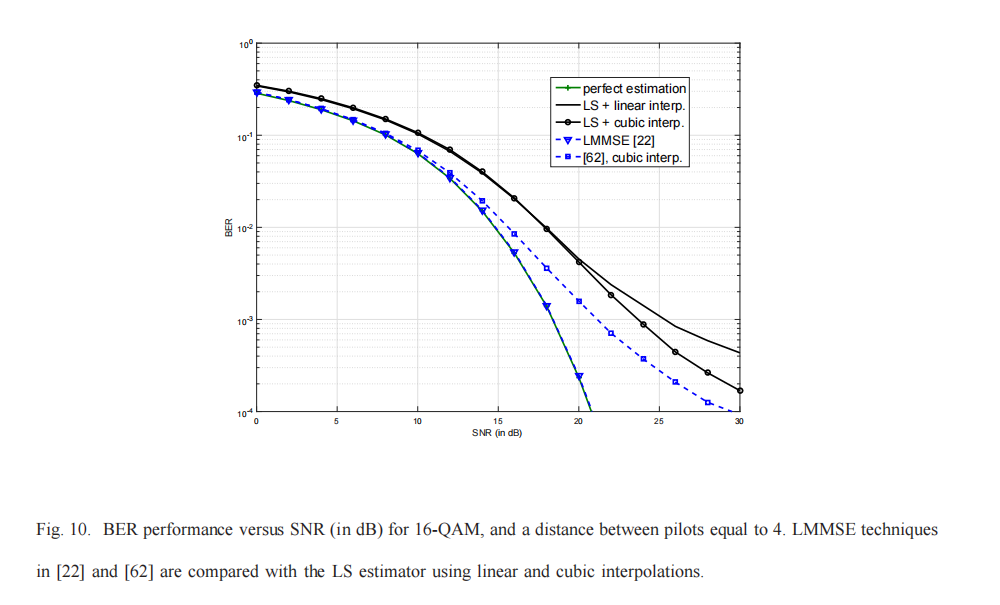
1.3 基于导频的信道与噪声估计
1.3.1 导频分布
主要的导频分布包含两种梳状和块状 两种:
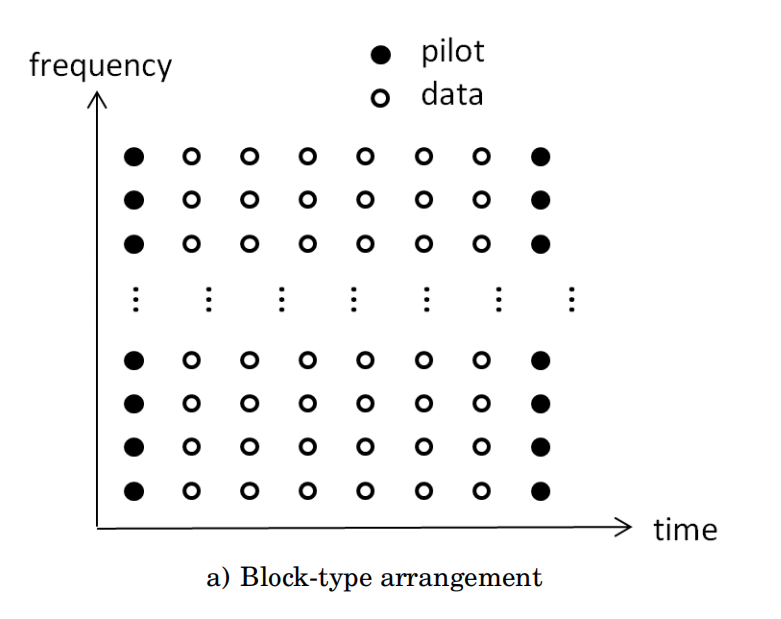
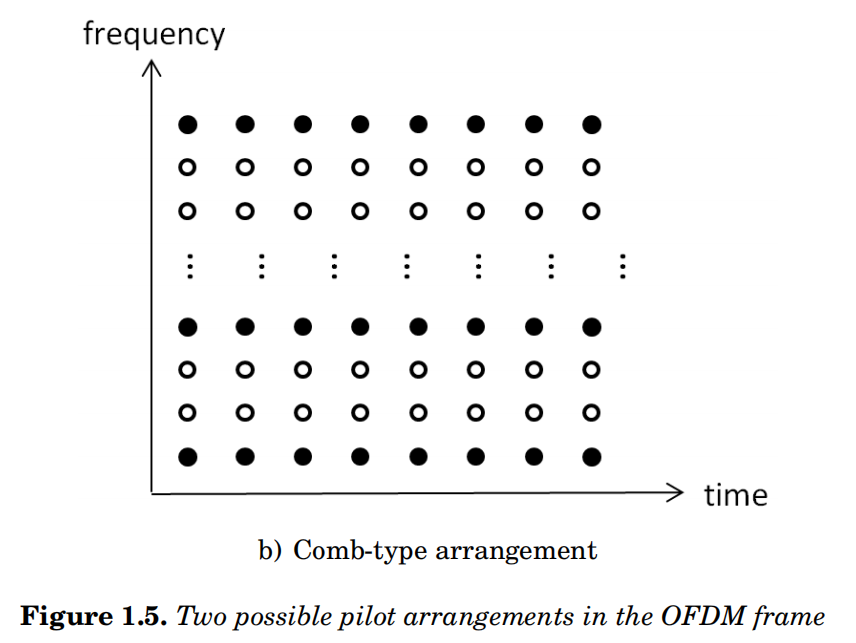
4G和5G系统中主要使用块状导频即图1.5,当然为了减小开销只是部分导频和符号才会插入导频,导频位置是不允许发送发送数据。
1.3.2 信道估计
目前主要使用的信道估计算法包含最小二成(LSLSLS)和线性最小均方误差(LMMSELMMSELMMSE),主要原因是这两种方法是研究最多也是最成熟的方法。其他文章已经介绍过其具体数学原理,所以下面介绍的时候我们直接引用。
1.3.2.1 LSLSLS信道估计
LSLSLS准则的目标是最小化其代价函数JLSJ_{LS}JLS,其定义了接收信号Y\mathbf{Y}Y与发送信号X\mathbf{X}X经过系数D\mathbf{D}D变换后距离的平方。JLSJ_{LS}JLS定义如下:
JLS=∣Y−DX∣2(1.21) J_{LS}=|\mathbf{Y-DX}|^2 \tag{1.21} JLS=∣Y−DX∣2(1.21)
定义最后化矩阵D=H^LS\mathbf{D=\hat{H}^{LS}}D=H^LS,H^LS\mathbf{\hat{H}^{LS}}H^LS就是LSLSLS需要估计的CFR。经过推导后可得:
H^mLS=YmXm=Hm+WmXm(1.22) \hat{H}{m}^{LS}=\frac{Y{m}}{X_{m}}=H_{m}+\frac{W_{m}}{X_{m}}\tag{1.22} H^mLS=XmYm=Hm+XmWm(1.22)
通过上式可看出LSLSLS估计对噪声特别敏感,因此后续一般会进行一个WINNER滤波。
1.3.2.2 2-D Wiener 滤波
OFDM系统中由于存在时间域和频域两个维度所以一般会进行一个二维的Wiener 滤波。如图1.6所示位置(p,np)∈Ω(p,n_{p})\in\Omega(p,np)∈Ω是导频位置,Wiener 滤波即是要估计出数据子载波(m,n)(m,n)(m,n)的信道响应:
H^m,n=∑(p,np)∈ΩG(m,n,p,np)H^p,npLS(1.23) \hat{H}{m,n}=\sum{(p,n_p)\in\Omega}G(m,n,p,n_p)\hat{H}_{p,n_p}^{LS}\tag{1.23} H^m,n=(p,np)∈Ω∑G(m,n,p,np)H^p,npLS(1.23)
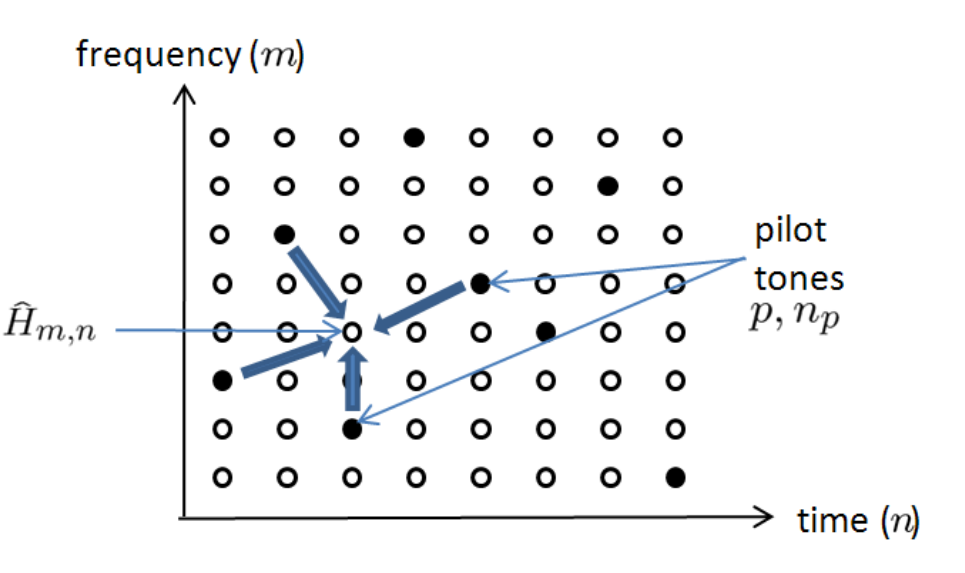
最优估计即最小化代价函数:
G(m,n)=min(E{∣Hm,n−H^m,n∣2})(1,24) G(m,n)=min\left(E\{|H_{m,n}-\hat{H}_{m,n}|^2\} \right)\tag{1,24} G(m,n)=min(E{∣Hm,n−H^m,n∣2})(1,24)
G(m,n)G(m,n)G(m,n)相当于一个时域和频域的插值滤波系数,所以又叫做2-D Wiener滤波。为了降低计算复杂度又提出了在时域和频域分别滤波的方式 ,很多参考文献又称其为LMMSELMMSELMMSE.实际上这两种在线性系统和高斯白噪声条件下是等价的。
1.3.2.3 LMMSELMMSELMMSE 信道估计(滤波)
LMMSELMMSELMMSE沿着时域和频域分别进行滤波如下图所示:
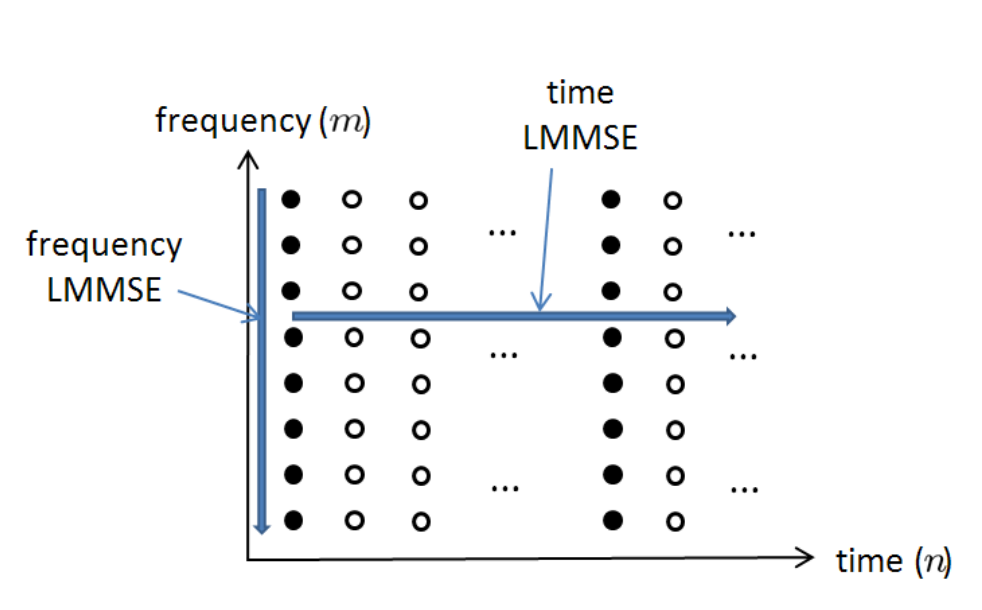
其代价函数为JMMSE=E{∥Hn−DYn∥2}J_{MMSE}=E\{\parallel H_n-DY_n\parallel^2\}JMMSE=E{∥Hn−DYn∥2},DDD是带估计的系数矩阵,信道冲击响应的H^nLMMSE\hat{H}n^{LMMSE}H^nLMMSE可以表示为:
H^nLMMSE=DoptH^nLS=RHH(RHH+σ2I)−1H^nLS \begin{align*} \hat{H}n^{LMMSE}&=D{opt}\hat{H}{n}^{LS}\tag{1.25}\\ &=R_{HH}(R_{HH}+\sigma^2I)^{-1}\hat{H}_{n}^{LS} \end{align*} H^nLMMSE=DoptH^nLS=RHH(RHH+σ2I)−1H^nLS(1.25)
其中Dopt=RHH(RHH+σ2I)−1H^nLSD_{opt}=R_{HH}(R_{HH}+\sigma^2I)^{-1}\hat{H}n^{LS}Dopt=RHH(RHH+σ2I)−1H^nLS,其中RHH=E{HHH}R{HH}=E\{HH^H\}RHH=E{HHH}为信道的协方差矩阵。LMMSELMMSELMMSE 信道估计最大的一个问题就是信道的相关矩阵计算,其直接影响信道估计的准确度。实时计算一般很难,很多文献包括3GPP研究了在统计情况下信道分布。如果是WUSS信道频域相关矩阵是其功率时延谱的傅里叶变换。比较常用的功率时延分布是指数分布所以:
(RH,f)μ,ν=FTτ(Ce−τ/τmax)=LC⋅1−e−2jπu−vMτmax−11+2jπu−vMτmax \begin{align*} (R_{H,f}){\mu,\nu}&=FT{\tau}(Ce^{-\tau/\tau_{max}})\\ &=LC \cdot \frac{1 - e^{-2j\pi \frac{u-v}{M} \tau_{max} - 1}}{1 + 2j\pi \frac{u-v}{M} \tau_{max}}\tag{1.26} \end{align*} (RH,f)μ,ν=FTτ(Ce−τ/τmax)=LC⋅1+2jπMu−vτmax1−e−2jπMu−vτmax−1(1.26)
其中μ−ν\mu-\nuμ−ν为子载波间隔(上述只是进行一个示例,因为参考模型不同最终的结果也不相同),τmax\tau_{max}τmax为最大的时延delay。
时域信道模型一般参考Jakes模型,功率谱称为U型谱时域相关矩阵如下:
(RH,t)u,v=F−1{U(f)}=σh2J0 (2πνDmax(u−v)),(1.27) \begin{aligned} \left(\mathbf{R}{H,t}\right){u,v} &= \mathcal{F}^{-1}\{U(f)\} \\ &= \sigma_h^2 J_0\!\big(2\pi\nu_{D_{\max}}(u-v)\big),\tag{1.27} \end{aligned} (RH,t)u,v=F−1{U(f)}=σh2J0(2πνDmax(u−v)),(1.27)
其中U(f)U(f)U(f)是Jakes频谱,νDmax\nu_{D_{max}}νDmax是最大多普勒频移,J0J_{0}J0是第一类0阶贝塞尔函数。
如上式子1.26和1.27所示其相关矩阵依赖于信道的统计特性,如功率时延谱、多普勒功率谱、时延、多普勒,然而这些参数在接收端一般是不知道的。这也是LMMSELMMSELMMSE难以在工程中使用的原因。当然也有很多文章进行RHHR_{HH}RHH的估计,实际中很多都是根据统计特性或者仿真结果预先存储。
1.2.2.4 LMMSELMMSELMMSE 插值滤波
因为导频在OFDM系统中是稀疏的,因此无法获得所有位置的信道冲击响应,需要一种插值算法。所有H^n,M×1LMMSE\hat{H}{n,M\times 1}^{LMMSE}H^n,M×1LMMSE可通过H^n,Np×1LS\hat{H}{n,N_{p}\times 1}^{LS}H^n,Np×1LSWiener 滤波获得:
H^n,M×1LMMSE=RH,M×Np(RH,Np×Np+σ2I)−1H^n,Np×1LS \begin{align*} \hat{H}{n,M\times 1}^{LMMSE}={\color{red}R{H,M\times N_{p}}}({\color{blue}{R_{H,N_{p}\times N_{p}}}} + \sigma^2I)^{-1}\hat{H}{n,N{p}\times 1}^{LS} \tag{1.28} \end{align*} H^n,M×1LMMSE=RH,M×Np(RH,Np×Np+σ2I)−1H^n,Np×1LS(1.28)
RH,Np×Np{\color{blue}{R_{H,N_{p}\times N_{p}}}}RH,Np×Np为导频间的自相关矩阵,RH,M×Np{\color{red}R_{H,M\times N_{p}}}RH,M×Np为数据与导频间的互相关矩阵。滤波的时候一般RH,Np×Np=RH,M×Np{\color{blue}{R_{H,N_{p}\times N_{p}}}} = {\color{red}R_{H,M\times N_{p}}}RH,Np×Np=RH,M×Np,当然也可能不相同(即滤波输出的位置不是导频位置,相当于一个插值)。插值的时候RH,Np×Np!=RH,M×Np{\color{blue}{R_{H,N_{p}\times N_{p}}}} != {\color{red}R_{H,M\times N_{p}}}RH,Np×Np!=RH,M×Np。如上如果使用LSLSLS,H^n,Np×1LS\hat{H}{n,N{p}\times 1}^{LS}H^n,Np×1LS 则可已直接使用式1.28. 当然也可直接使用H^n,Np×1LMMSE\hat{H}{n,N{}p\times 1}^{LMMSE}H^n,Np×1LMMSE,因为其已经是滤波后的结果所以式子1.28可能会变换成(这个不确定):
H^n,M×1LMMSE=RH,M×Np(RH,Np×Np+(σ2I)→0)−1H^n,Np×1LMMSE \begin{align*} \hat{H}{n,M\times 1}^{LMMSE}={\color{red}R{H,M\times N_{p}}}({\color{blue}{R_{H,N_{p}\times N_{p}}}} + {\color{brown}{(\sigma^2I){\rightarrow 0}}})^{-1}\hat{H}{n,N_{p}\times 1}^{LMMSE} \tag{1.29} \end{align*} H^n,M×1LMMSE=RH,M×Np(RH,Np×Np+(σ2I)→0)−1H^n,Np×1LMMSE(1.29)
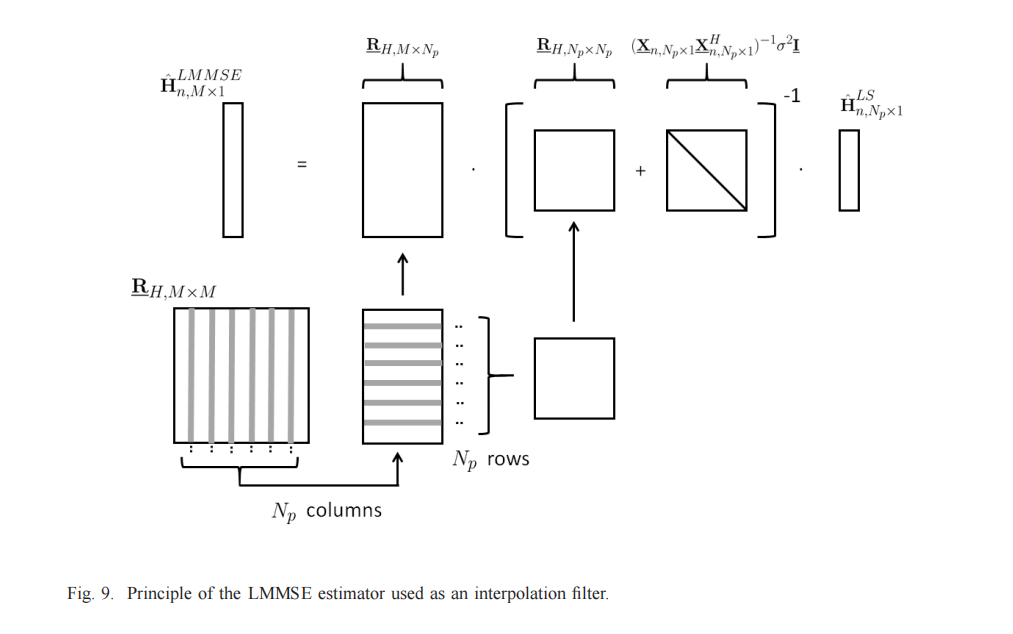
如上图所示RH,M×MR_{H,M\times M}RH,M×M为所有子载波的位置的互相关矩阵,RH,M×NPR_{H,M\times N_{P}}RH,M×NP和RH,Np×NpR_{H,N_{p}\times N_{p}}RH,Np×Np都是其中的子集按照滤波和插值自行选取。当然实际使用时为了减少计算量可进行适当简化:
1,不论是插值还是滤波都只是选取适当的tap进行操作。
2,上式还可以进行SVD分解减少计算量。
3,在固定tap和导频位置情况下,直接将系数计算公式省略直接存在最终的系数。