从零开始刷算法——贪心篇1:跳跃游戏1 + 跳跃游戏2

在 LeetCode 的贪心算法专题中，跳跃游戏 (Jump Game) 系列是两座必须翻越的大山。

这两道题虽然都叫"跳跃"，但考察的侧重点略有不同：

55. 跳跃游戏 ：考察 可达性（能不能跳到终点？）。
45. 跳跃游戏 II ：考察 最优解（最少跳几次能到终点？）。

虽然目标不同，但它们的灵魂都是一样的------贪心 (Greedy) 。即：在每一步都做出当前看起来最好的选择，从而导致全局的最优结果。

今天我们就通过这两段高效的 C++ 代码，来彻底拆解它们的逻辑。

Part 1：跳跃游戏 I ------ 我到底能跑多远？

核心思路：维护"最大覆盖范围"

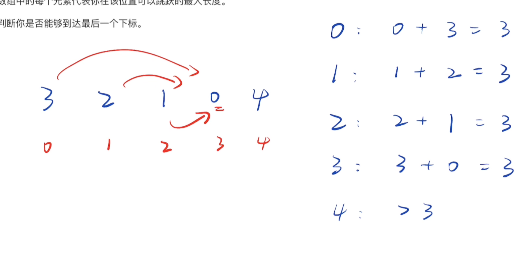
这道题问的是"能不能到达最后一个下标"。我们可以转换一下思维：我不关心具体怎么跳，我只关心我在当前位置，最远能覆盖到哪里。

我们维护一个变量 maxp (max position)，代表"当前能到达的最远位置"。

我们遍历数组中的每一个位置 i。
生死线判断 ：如果当前位置 i 居然比 maxp 还大（i > maxp），说明前面的所有跳跃加起来都够不到这里。既然连这里都到不了，那后面的终点更别想了，直接判死刑 (return false)。
贪心更新 ：如果能到达 i，那我们就看看从 i 起跳能不能把 maxp 推得更远。公式：maxp = max(maxp, i + nums[i])。

代码实现

C++代码实现：

cpp 复制代码

class Solution {
    // 思路： 维护一个可以跳跃的最大值， 如果这个最大值小于i，说明i不可达到直接返回false
    // 否则我们更新最大值maxp，最后如果for可以执行完， 就直接返回true
public:
    bool canJump(vector<int>& nums) {
        // i 是当前所在位置，maxp 是目前能摸到的最远边界
        for (int i = 0, maxp = 0; i < nums.size(); ++i) {
            // 如果当前位置已经超过了最大覆盖范围，说明断档了，过不去
            if (maxp < i) return false;
            else {
                // 贪心：不断刷新能覆盖的最远距离
                maxp = max(maxp, i + nums[i]);
            }
        }
        return true;
    }
};

复杂度分析

时间复杂度：O(N)。我们需要遍历一遍数组，每个元素访问一次。
空间复杂度：O(1) 。只用了 i 和 maxp 两个变量，不需要额外的数组空间。

Part 2：跳跃游戏 II ------ 如何用最少的步数到达？

核心思路：步步为营的"边界推进"

这道题难度升级了，要求最小跳跃次数。这也是典型的贪心，但策略稍微复杂一点。

我们需要维护两个关键变量：

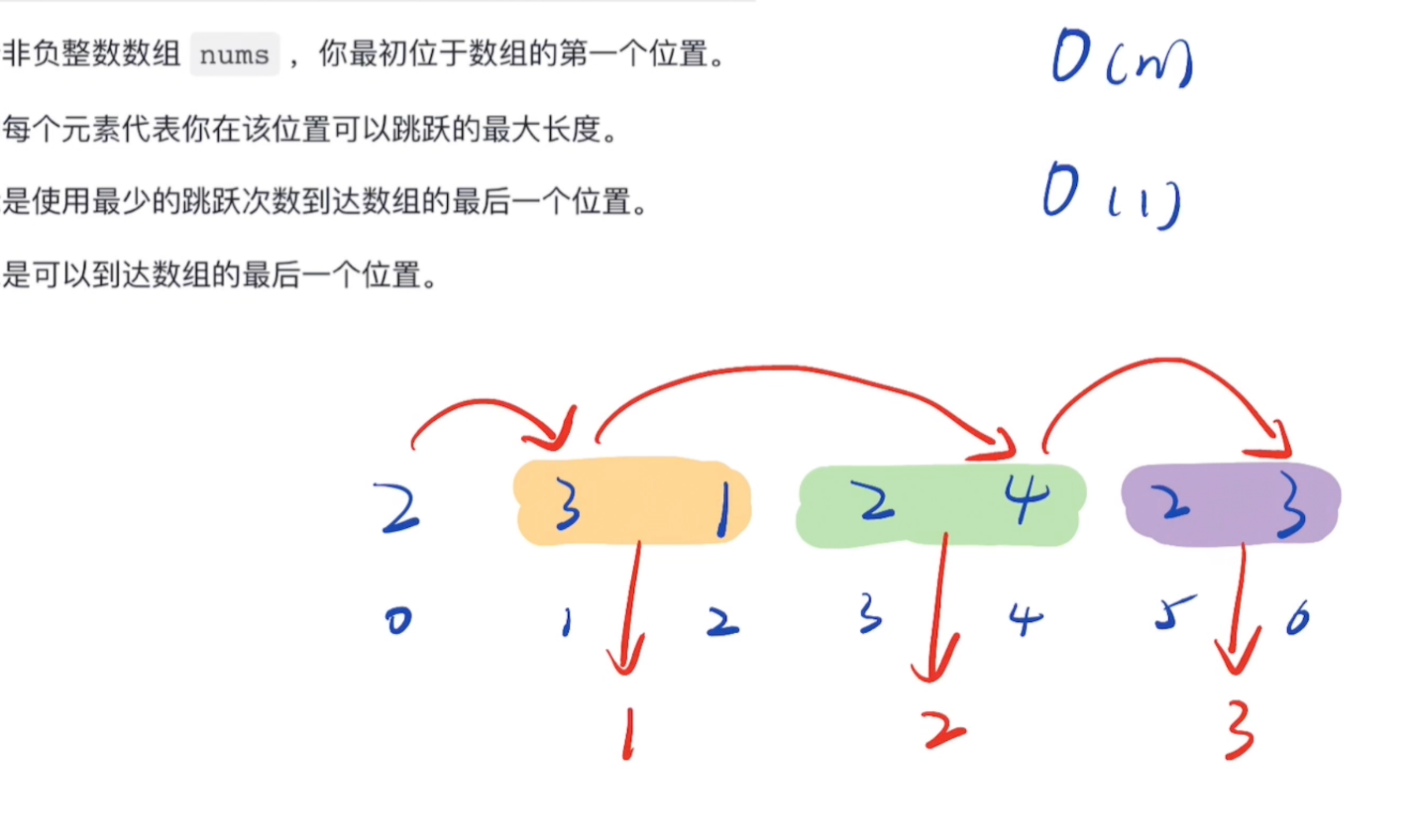
end (当前边界)：这一步跳跃（比如说第 1 步）最远能覆盖到的位置。
maxp (下一跳潜力)：在当前这一步的覆盖范围内，我们寻找的所有落脚点中，下一跳能到达的最远位置。

贪心逻辑演示： 想象你在开车，end 是你油箱里剩下的油能开到的最远距离。在你从起点开到 end 的过程中，你会经过很多加油站（数组下标）。 你的策略是 ：在到达 end 之前，把所有加油站都看一遍，记下哪个加油站能让你下一次 跑得最远（更新 maxp）。当你真的开到 end（油耗尽了），你就必须加油（跳跃次数 ans++），而新的油量能让你跑多远呢？就是你刚才一路观察下来的最大值 maxp。

为什么循环只到 `size - 1`？

这是一个很多人的盲点。

i 代表的是 "起跳点"。
最后一个位置是 "终点"。
我们只需要保证能跳到终点即可，不需要从终点再跳一次。所以遍历的时候，不需要考虑最后一个位置作为起跳点。

代码实现

C++代码实现：

cpp 复制代码

class Solution {
    // 思路： 在当前我能到达的所有位置中，我总是去寻找那个能帮我跳得最远的位置，作为我的下一次起跳点。（贪心） 
    // 同时更新区间 end：我当前可以跳跃到的最远位置 
    // 和 maxp：代表从当前位置到 end 之间，我能探索到的下一跳的最远位置。
public:
    int jump(vector<int>& nums) {
        int ans = 0;
        int end = 0, maxp = 0;
        
        // 贪心算法不是"真的跳过去了"，而是**"在这个范围内所有能落脚的点都看一遍"**，
        // 选出最强的那个作为下一步的基石。所以绝对不会错过中间的超级跳板。
        // 注意这里的 i 是遍历的可能作为起跳点的位置，所以只到 nums.size() - 2
        for (int i = 0; i < nums.size() - 1; ++i) {
            // 1. 扫描：在当前步数的覆盖范围内，寻找下一跳的最强落点
            maxp = max(maxp, i + nums[i]);
            
            // 2. 结算：遇到了当前步数的边界
            if (end == i) {
                end = maxp; // 更新边界：下一跳的最远距离就是刚才找到的最大值
                ans++;      // 步数 +1
            }
        }
        return ans;
    }
};

复杂度分析

时间复杂度：O(N) 。虽然是贪心，但我们只遍历了一次数组。代码中的 i 从头走到尾，并没有回溯，也没有嵌套循环。
空间复杂度：O(1) 。只使用了 ans, end, maxp 几个变量，原地解决问题。

总结

这两道题完美展示了贪心算法的魅力：不追求穷举所有可能性（那是动态规划的事情），而是通过局部最优决策，直接逼近全局最优。

题目 I 告诉我们：维护一个不断生长的 maxp，只要 i 不掉队，就能到达终点。
题目 II 告诉我们：把跳跃看作是"一段一段"的区间推进。在到达当前区间边界 end 之前，尽可能把下一次的边界 maxp 撑得更大。

一句话口诀： I 看能不能覆盖，II 看边界怎么推。记住 size-1 是起跳点的极限。

从零开始刷算法——贪心篇1:跳跃游戏1 + 跳跃游戏2

Part 1：跳跃游戏 I ------ 我到底能跑多远？

核心思路：维护"最大覆盖范围"

代码实现

复杂度分析

Part 2：跳跃游戏 II ------ 如何用最少的步数到达？

核心思路：步步为营的"边界推进"

为什么循环只到 size - 1？

代码实现

复杂度分析

总结

为什么循环只到 `size - 1`？