优选算法-字符串

算法原理

字符串类型的算法题最重要的是模拟,考验的是代码能力

题目解析

1.最长公共前缀

https://leetcode.cn/problems/longest-common-prefix/description/

题目描述

查找字符串数组中最长公共前缀,如果没有的话,返回空

eg: strs=["flower","flow","flight"] return"fl";

算法原理

解法一:两两比较(双指针)

解法二:统一比较(有不一样的立即停止/有字符串结束时也需要立刻停止)

代码实现

java 复制代码

class Solution {
    public String longestCommonPrefix(String[] strs) {
        //统一比较
        for(int i=0;i<strs[0].length();i++){
            char tmp=strs[0].charAt(i);
            for(int j=1;j<strs.length;j++){
                if(i==strs[j].length()||strs[j].charAt(i)!=tmp){
                    return strs[0].substring(0,i);
                }
            }
        }
        return strs[0];
    }
}

2.最长回文子串

https://leetcode.cn/problems/longest-palindromic-substring/description/

题目描述

给定一个字符串s,找到s中最长的回文子串

eg: s="babad"-->return "bab" "aba"

s="cbbd"-->return "bb"

算法原理

解法:中心拓展算法(暴力枚举&&利用回文串的特性)

可以定义一个begin 和len,这样更易于返回结果

从字符串的第一个字符串开始,一个一个遍历(一个是奇数方式的遍历,一个是偶数方式的遍历)

当数组越界/不满足回文串的特性时,我们就需要更新结果,这里注意begin=left+1(因为出while循环的时候left已经不满足条件了而left+1满足条件)

同时注意更新len(len=right-left-1);

代码实现

java 复制代码

class Solution {
    public String longestPalindrome(String s) {
        int n=s.length();
        int begin=0;
        int len=0;
        for(int i=0;i<n;i++){
            int left=i;
            int right=i;
            while(left>=0&&right<n&&s.charAt(left)==s.charAt(right)){
                left--;
                right++;
            }
            if(right-left-1>len){
                begin=left+1;
                len=right-left-1;
            }
            left=i;
            right=i+1;
             while(left>=0&&right<n&&s.charAt(left)==s.charAt(right)){
                left--;
                right++;
            }
            if(right-left-1>len){
                begin=left+1;
                len=right-left-1;
            }
        }
        return s.substring(begin,begin+len);
    }
}

3.二进制求和

https://leetcode.cn/problems/add-binary/description/

题目描述

给定一个二进制字符串a和b,以二进制字符串的形式返回他们的和(二进制求和,高精度加法本质是模拟)

算法原理

解法:模拟列竖式计算(两个1的话就要向上进了,并且第一个不能是0,必须是1)

代码实现

java 复制代码

class Solution {
    public String addBinary(String a, String b) {
        int cur1=a.length()-1,cur2=b.length()-1,t=0;
        StringBuffer ret=new StringBuffer();
        while(cur1>=0||cur2>=0||t!=0){
            if(cur1>=0){
                t+=a.charAt(cur1--)-'0';
            }
            if(cur2>=0){
                t+=b.charAt(cur2--)-'0';
            }
            ret.append((char)('0'+t%2));
            t/=2;
        }
        ret.reverse();
        return ret.toString();
    }
}

4.字符串相乘

https://leetcode.cn/problems/multiply-strings/description/

题目描述

给定两个以字符串形式表示的非负整数num1和num2 ,返回num1和num2的乘积,由字符串返回

算法原理

解法一:模拟列竖式计算

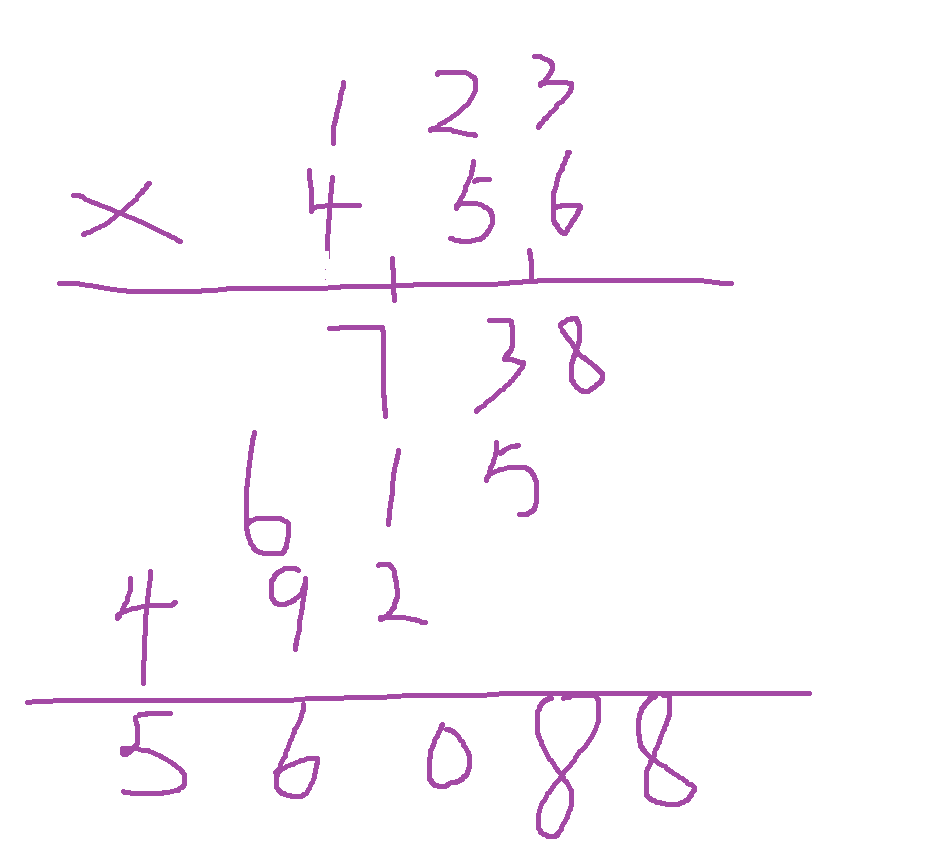
细节1:高位相乘要补0(逆序加0的数)

细节2:处理前导0

细节3:注意计算结果的顺序

解法二:对解法一进行优化-->无进位相乘相加,最后处理进位

代码实现

java 复制代码

class Solution {
    public String multiply(String num1, String num2) {
        int m=num1.length(),n=num2.length();
        int[] tmp=new int[m+n-1];
        char[] n1=new StringBuffer(num1).reverse().toString().toCharArray();
        char[] n2=new StringBuffer(num2).reverse().toString().toCharArray();
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                tmp[i+j]+=(n1[i]-'0')*(n2[j]-'0');
            }
        }
        int cur=0,t=0;
        StringBuffer ret=new StringBuffer();
        while(cur<m+n-1||t!=0){
            if(cur<m+n-1)
            t+=tmp[cur++];
            ret.append((char)((char)(t%10)+'0'));
            t/=10;
        }
        while(ret.length()>1&&ret.charAt(ret.length()-1)=='0'){
            ret.deleteCharAt(ret.length()-1);
        }
        return ret.reverse().toString();
    }
}