深度学习---基础统计学
学习均值、中位数、众数、方差和标准差
一、为什么机器学习离不开统计学?
在机器学习中,我们处理的从来不是"一个数据",而是一大堆样本、一整个分布。
这也是为什么,在正式讨论模型结构、损失函数或优化算法之前,我们必须先理解---数据本身长什么样。
-
描述性统计,正是用来概括和描述数据分布特征的工具。
-
想象一下你上学期的考试成绩:如果我让你记住每一科的分数,几乎不可能;但如果我告诉你:
- 平均分是多少
- 成绩是否集中
- 有没有极端高分或低分
你立刻就能对整体表现有一个清晰的判断。
**这正是统计学的价值:**将成千上万的数字,压缩成少量却信息密度极高的指标。
-
而在机器学习中:
- 模型训练是否稳定
- 初始化是否合理
- 特征是否需要 Normalize
- 梯度是否容易爆炸或消失
几乎都可以追溯到这些最基础的统计量。
二、平均值(Mean)
在对一组数据进行整体分析时,最常见、也最直观的做法,是寻找一个能够代表"典型样本"的中心值,**平均值(Mean)**正是最常用的中心度量方式。
-
从直觉上看,平均值回答的是这样一个问题:如果所有样本都"趋向同一个水平",这个水平会是多少?
正因为这种"整体平衡"的含义,平均值在统计分析和机器学习中被大量使用。
2.1 定义
算术平均值定义为:将所有观测值相加,再除以观测值的数量。
如果一组数据为:x1,x2,⋯ ,xnx_1, x_2, \cdots, x_nx1,x2,⋯,xn,则其平均值为:
μ=1n∑i=1nxi=x1+x2+⋯+xnn \mu = \frac{1}{n}\sum_{i=1}^{n} x_i = \frac{x_1+x_2+\cdots+x_n}{n} μ=n1i=1∑nxi=nx1+x2+⋯+xn
这也是日常生活中人们最常提到的"平均数"。
-
示例:灯泡寿命
假设我们测试了 5 个灯泡,其使用寿命分别为:
980, 1000, 1010, 1020, 1040(小时) 980,\;1000,\;1010,\;1020,\;1040 \quad (\text{小时}) 980,1000,1010,1020,1040(小时)根据平均值的定义,它们的算术平均值为:
Mean=980+1000+1010+1020+10405=1010 小时 \text{Mean} = \frac{980 + 1000 + 1010 + 1020 + 1040}{5} = 1010\;\text{小时} Mean=5980+1000+1010+1020+1040=1010小时 这意味着,如果用一个数来概括这 5 个灯泡的整体寿命水平,那么 1010 小时 是最常用、也最直观的代表值。在机器学习中,很多模型在最小化平方误差时,学到的预测值,本质上就是在寻找这样的"平均水平"。
2.2 为什么平均值在机器学习中如此重要?
平均值不仅是一个描述数据的统计量,它在机器学习中还隐含地定义了模型所"偏好"的中心位置:
- 在最小化平方误差(L2 Loss) 时,模型学到的最优预测值正是样本的平均值;
- 许多初始化方法(如 Xavier、Kaiming)都默认激活值或权重分布以零均值为中心;
- 数据标准化(Standardization)通常以"减去均值"作为第一步。
换句话说:**平均值往往是模型默认认为的"正常状态"。**理解这一点,对于后续理解损失函数设计、训练稳定性以及归一化操作至关重要。
2.3 一个重要的注意点
平均值对极端值(outliers)非常敏感。当数据中存在少量异常样本时,平均值可能会被明显拉偏,从而不再代表大多数样本的典型水平。这一问题,也正是中位数等其他中心度量存在的原因。
三、中位数(Median)
平均值适用于分布相对对称的数据,但它有一个显著的缺点:少量异常值(outliers)就可能使结果严重偏离真实的中心位置。
中位数通过一种不同的方式来定义"中心"---它关注的是数据的相对位置,而不是具体数值大小,因此对异常值更加稳健。
3.1 定义
将所有数据点按从小到大排序后:
-
如果数据点个数 nnn 为奇数,中位数是位于正中间的那个值;
-
如果数据点个数nnn为偶数,中位数是中间两个值的平均值。
形式化地表示为:
Median={xn+12,n 为奇数xn2+xn2+12,n 为偶数 \text{Median} = \begin{cases} x_{\frac{n+1}{2}}, & n \text{ 为奇数} \\ \frac{x_{\frac{n}{2}} + x_{\frac{n}{2}+1}}{2}, & n \text{ 为偶数} \end{cases} Median={x2n+1,2x2n+x2n+1,n 为奇数n 为偶数其中,xix_ixi表示排序后的第iii个数据点。
3.2 示例:存在异常值的灯泡寿命
假设我们测试了555个灯泡,其使用寿命分别为:
500, 980, 1000, 1010, 1020(小时) 500,\;980,\;1000,\;1010,\;1020 \quad (\text{小时}) 500,980,1000,1010,1020(小时)
其中,一个灯泡因质量问题提前失效,形成了明显的异常值。
将数据排序后得到:
500, 980, 1000, 1010, 1020 500,\;980,\;1000,\;1010,\;1020 500,980,1000,1010,1020
此时,中位数 = 1000 小时(位于中间的位置),平均值 = 500+980+1000+1010+10205=902 小时\frac{500 + 980 + 1000 + 1010 + 1020}{5} = 902 \;\text{小时}5500+980+1000+1010+1020=902小时
可以看到,平均值被异常值显著拉低,而中位数仍然稳定地反映了大多数灯泡的典型寿命水平。
3.3 为什么中位数在机器学习中很重要?
在真实数据中,噪声样本、标注错误、极端观测值几乎不可避免。
在这些场景下,中位数及其相关方法(如 L1 Loss、Huber Loss)往往比基于均值的方法更加稳健。
换句话说,当数据"不干净"时,中位数定义的中心,往往更接近模型真正应该学习的目标。
四、众数(Mode)
在某些情况下,我们并不关心"平均水平",也不关心"中间位置",而只是想知道:哪一个取值出现得最多?
这种需求在分类数据中尤为常见。由于类别本身没有数值大小关系,均值和中位数在这里往往失去意义,而众数则成为最自然的选择。
4.1 定义
众数(Mode)是指数据集中出现频率最高的取值。
-
需要注意的是:
- 一个数据集可能没有众数(所有值出现次数相同);
- 也可能只有一个众数(单峰);
- 或同时存在多个众数(双峰、多峰)。
众数并不依赖于数值大小,只与出现次数有关,因此既适用于数值型数据,也适用于分类型数据。
4.2 示例:分类数据中的灯泡质量等级
假设我们对一批灯泡进行了质量评级,得到如下结果:
良好, 良好, 良好, 优秀, 一般, 良好, 优秀 \text{良好},\; \text{良好},\; \text{良好},\; \text{优秀},\; \text{一般},\; \text{良好},\; \text{优秀} 良好,良好,良好,优秀,一般,良好,优秀
-
统计各类别的出现次数:
- 良好:4 次
- 优秀:2 次
- 一般:1 次
-
因此,该数据集的 众数 为:
Mode=良好 \text{Mode} = \text{良好} Mode=良好这意味着,在这批灯泡中,最常见、最具有代表性的质量等级是"良好"。
4.3 为什么众数在机器学习中很重要?
-
在分类任务中,标签本身是离散的、不可排序的,使用均值或中位数没有明确含义,众数天然地对应"最可能的类别"。
-
例如:
- 多分类模型中,预测概率最大的类别,本质上就是在寻找众数;
- 在类别极度不平衡的数据集中,"始终预测众数类别" 常被用作最简单的基线模型(baseline)。
因此,可以这样理解:众数定义了分类问题中最朴素、却无法回避的"默认预测"。
-
一个小提醒
虽然众数直观易懂,但当数据分布高度不平衡时,仅依赖众数可能会掩盖少数类别的重要信息。这也是为什么在实际建模中,我们往往需要结合其他指标(如精度、召回率、F1 分数)进行综合评估。
五、偏度(Skewness)
到目前为止,我们已经介绍了三种刻画数据"中心"的方法:均值、中位数和众数。但这里自然会产生一个问题:如果均值、中位数和众数给出的结果并不一致,该相信哪一个?
这种情况通常出现在数据分布不对称的时候。**偏度(Skewness)**正是用来描述数据分布形状的统计量,它刻画了分布是否左右平衡,还是在某一侧存在"长尾"。
-
直观理解
偏度关注的不是"中心在哪里",而是数据是对称分布的,还是被少数极端样本拉向了某一侧?
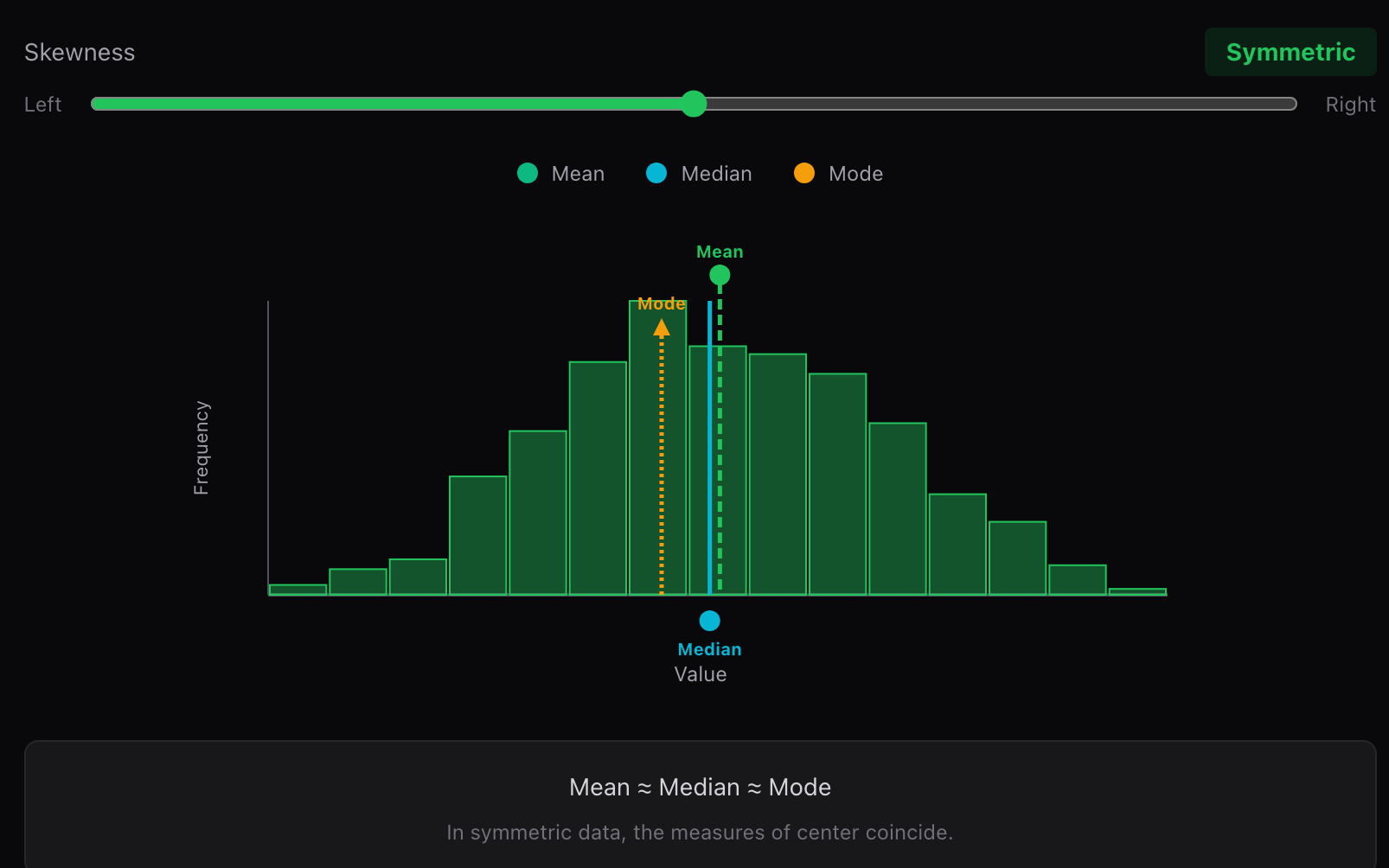
5.1 对称分布
当数据分布近似对称时:
偏度≈0均值≈中位数≈众数 \text{偏度} \approx 0 \\ \text{均值} \approx \text{中位数} \approx \text{众数} 偏度≈0均值≈中位数≈众数
此时,三种中心度量给出的结果基本一致,任何一种都可以较好地代表数据的典型水平。
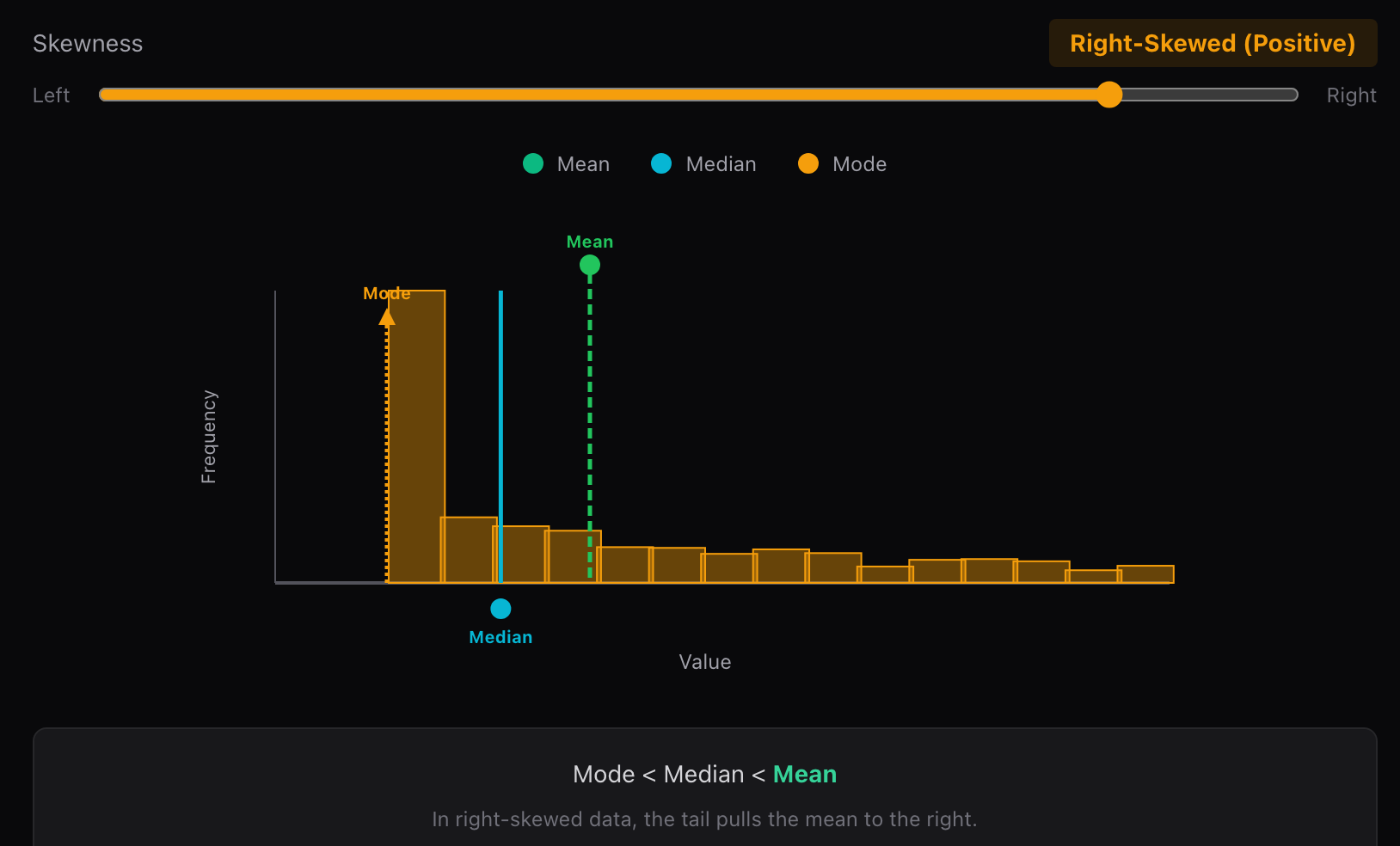
5.2 右偏分布(正偏,Positive Skew)
当分布右侧尾部较长 时,称为右偏分布。少量较大的极端值将均值向右拉动。
偏度>0 \text{偏度} > 0 偏度>0
- 此时通常有:
众数<中位数<均值 \text{众数} < \text{中位数} < \text{均值} 众数<中位数<均值
- 典型例子包括:收入、房价、等待时间等数据。
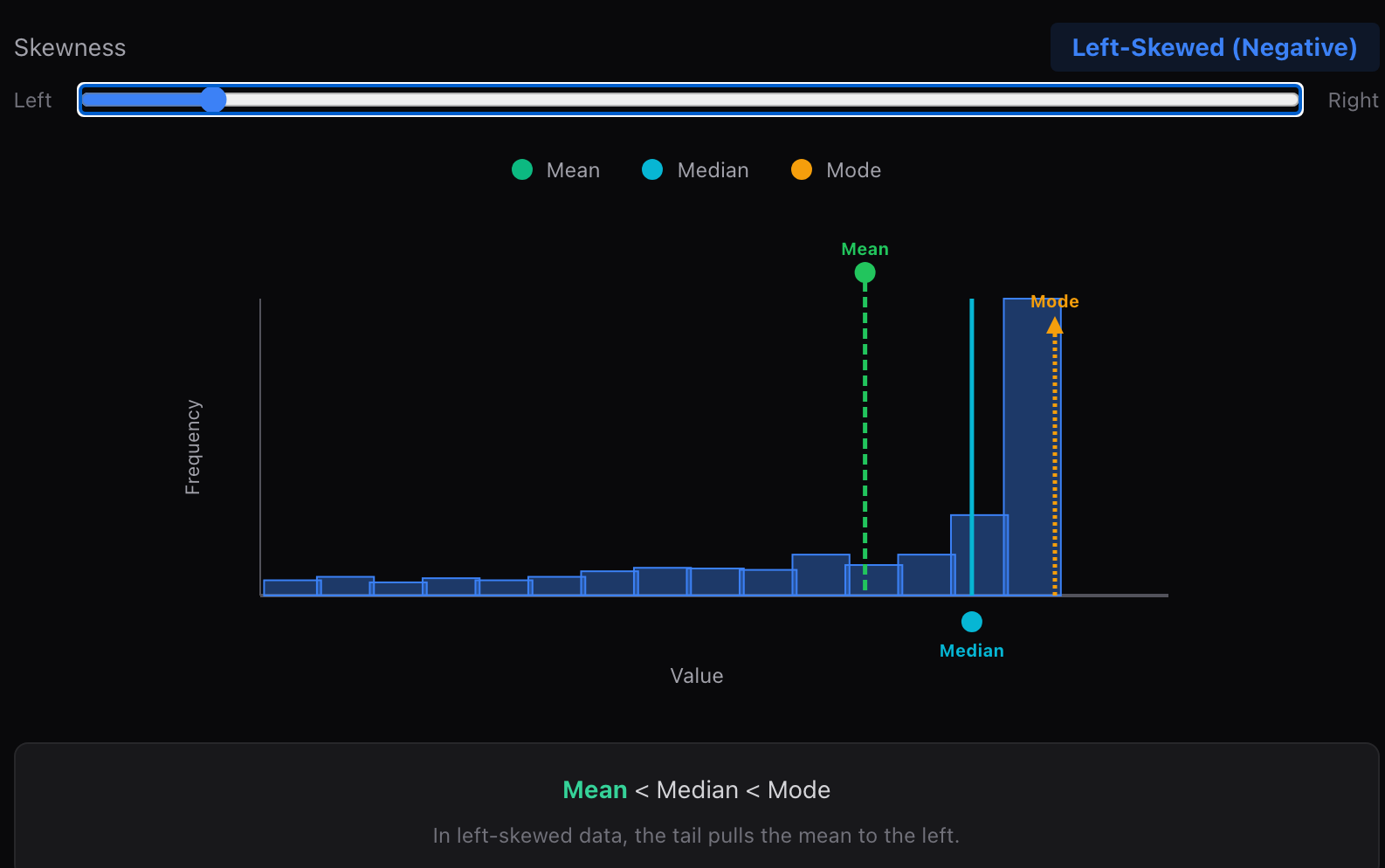
5.3 左偏分布(负偏,Negative Skew)
当分布左侧尾部较长 时,称为左偏分布。少量较小的极端值将均值向左拉动。
偏度<0 \text{偏度}<0 偏度<0
- 此时通常有:
均值<中位数<众数 \text{均值} < \text{中位数} < \text{众数} 均值<中位数<众数
这类分布在某些"有上限"的评分数据中较为常见。
5.4 为什么偏度在机器学习中很重要?
许多机器学习模型在设计时,隐含地假设输入数据近似对称或接近正态分布。
-
当数据存在严重偏度时,可能会带来:
- 梯度不稳定
- 损失函数被极端样本主导
- 模型更难收敛
-
例如,在房价预测中,少数豪宅可能会显著拉高平均值,使模型对"普通房屋"的预测产生系统性偏差。
-
因此,在实际建模前,我们常常会通过一些数学变换(如对数变换、Box-Cox 变换等),主动降低数据偏度,使分布更加对称。
-
一个经验性总结
当你发现均值、中位数和众数相差很大时,不妨先停下来看看数据的偏度。这往往是数据"在提醒你",当前分布可能并不符合模型的默认假设。
六、峰度(Kurtosis)
如果说偏度 描述的是数据分布的不对称性 ,那么**峰度(Kurtosis)**关注的则是另一件事:分布的尾部有多"重"?极端值出现的可能性有多大?
换句话说,峰度衡量的是异常值相对于正态分布出现得是否更频繁。
-
直观理解
峰度并不是在看"中间有多尖",而是在问:离中心很远的样本,是不是比我们预期的更多?因此,峰度对异常值极其敏感。
6.1 定义
峰度通常定义为标准化后数据的四阶中心矩 :
Kurtosis=1n∑i=1n(xi−xˉσ)4 \text{Kurtosis} = \frac{1}{n} \sum_{i=1}^{n} \left( \frac{x_i - \bar{x}}{\sigma} \right)^4 Kurtosis=n1i=1∑n(σxi−xˉ)4
其中,xˉ\bar{x}xˉ为均值,σ\sigmaσ为标准差。
由于采用了 四次方,距离均值较远的样本会被显著放大,这使得峰度能够有效捕捉尾部的厚薄程度。
6.2 不同峰度对应的分布形态
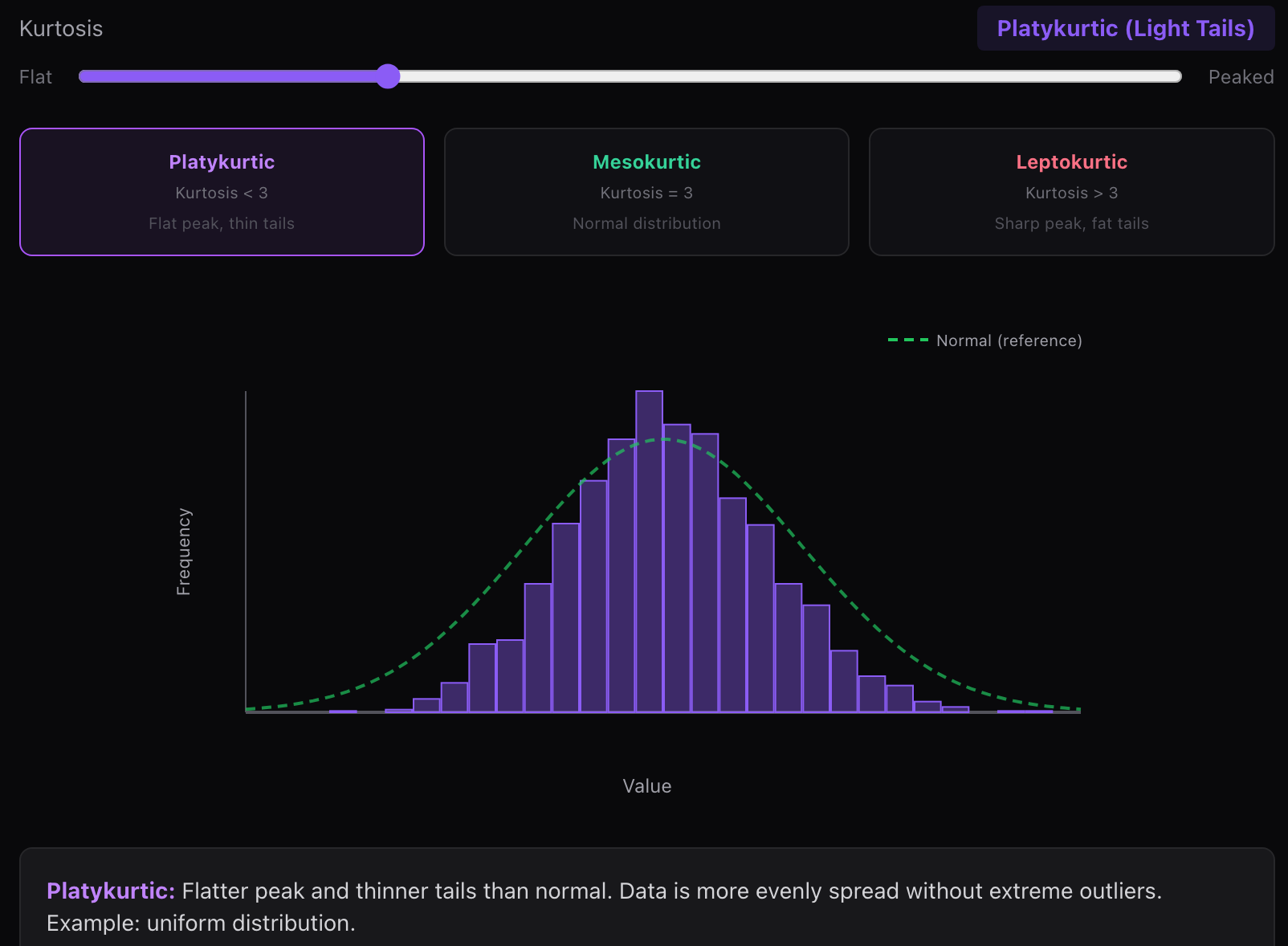
(1) 扁平峰(低峰度)
峰度 < 3,分布形态更平缓,尾部更细,极端值较少
- 峰形比正态分布更平缓,尾部更细。数据分布更均匀,没有极端异常值。例如:均匀分布。
- 这类分布的样本通常较为均匀,不容易出现远离均值的观测值。
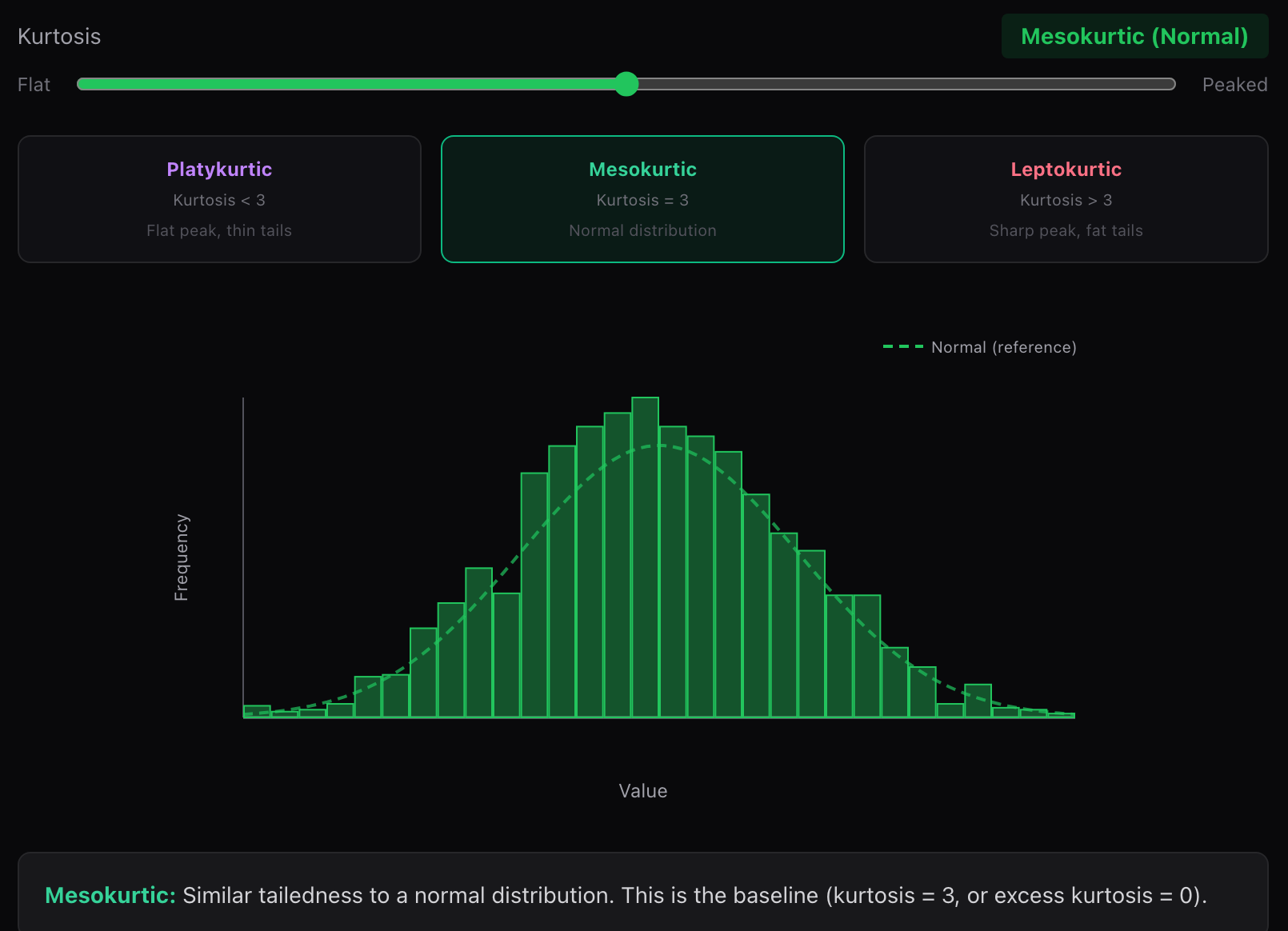
(2) 中峰(正态分布)
峰度 = 3,对应标准正态分布,常作为比较基准。
- 很多统计方法和机器学习模型,隐含地以这一情况作为默认参考。
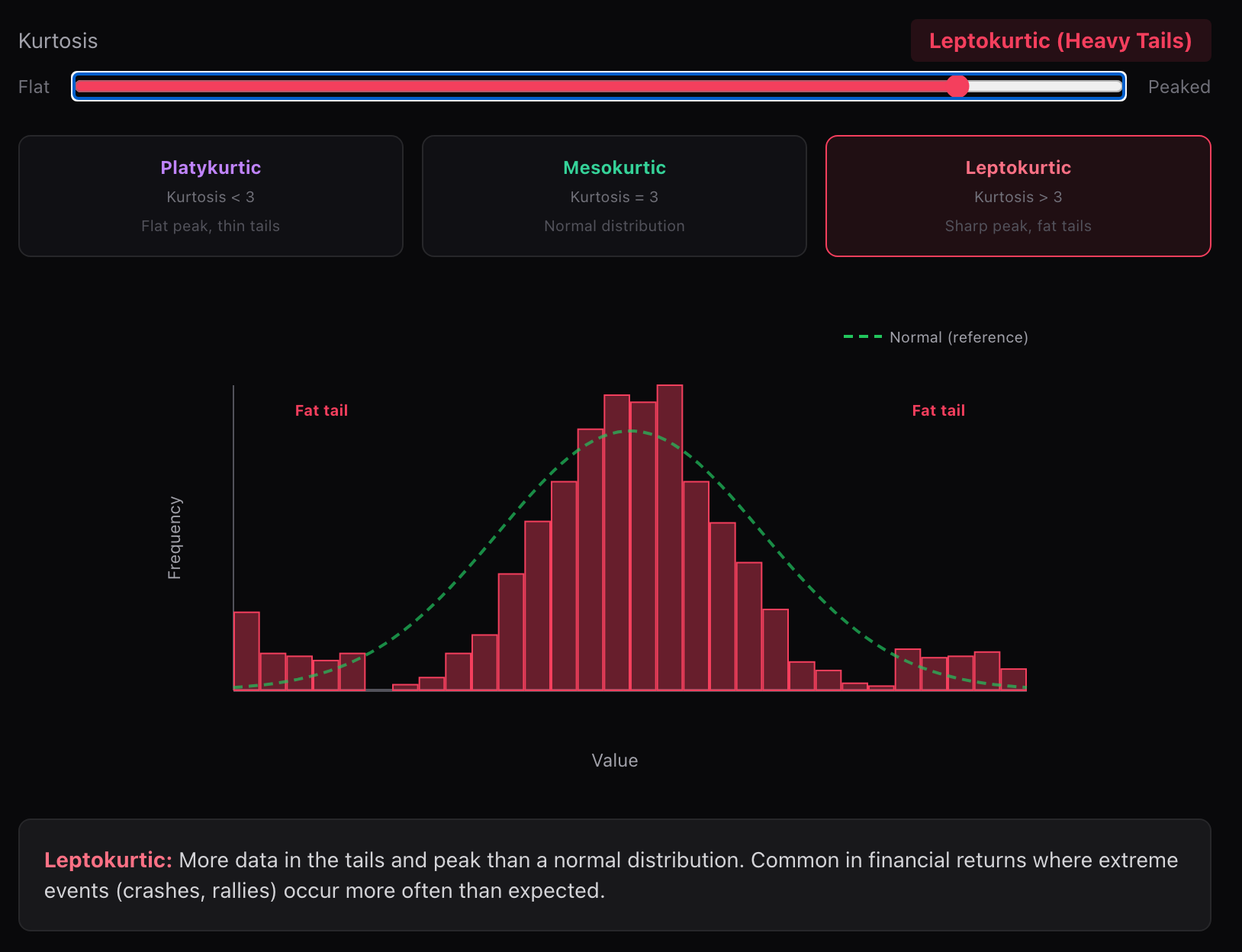
(3) 尖峰(高峰度)
峰度 > 3,分布中心更集中,尾部更厚,极端值更多。
- 与正态分布相比,数据在尾部和峰值处更为集中。这在金融收益中很常见,因为极端事件(崩盘、反弹)的发生频率高于预期。
- 这意味着大部分样本看起来很"正常",但偶尔会出现非常极端的异常值。
6.3 为什么峰度在机器学习中很重要?
-
高峰度数据往往意味着:
- 梯度更新容易被少数极端样本主导
- 均值和方差估计不稳定
- 模型对异常值高度敏感
-
在深度学习中,激活值或梯度如果呈现高峰度分布,可能导致训练震荡甚至数值不稳定。
-
因此,在建模前或训练过程中,人们常会通过数据变换、正则化、归一化或裁剪(clipping)来控制尾部行为,降低峰度带来的风险。
-
一个经验性总结
偏度告诉你"数据往哪边歪",峰度提醒你"尾巴到底有多危险"。
当你的数据既偏又"厚尾"时,往往需要格外小心模型假设与训练稳定性。