射频网课学习第二章(阻抗匹配 ch2-5到ch2-9部分)

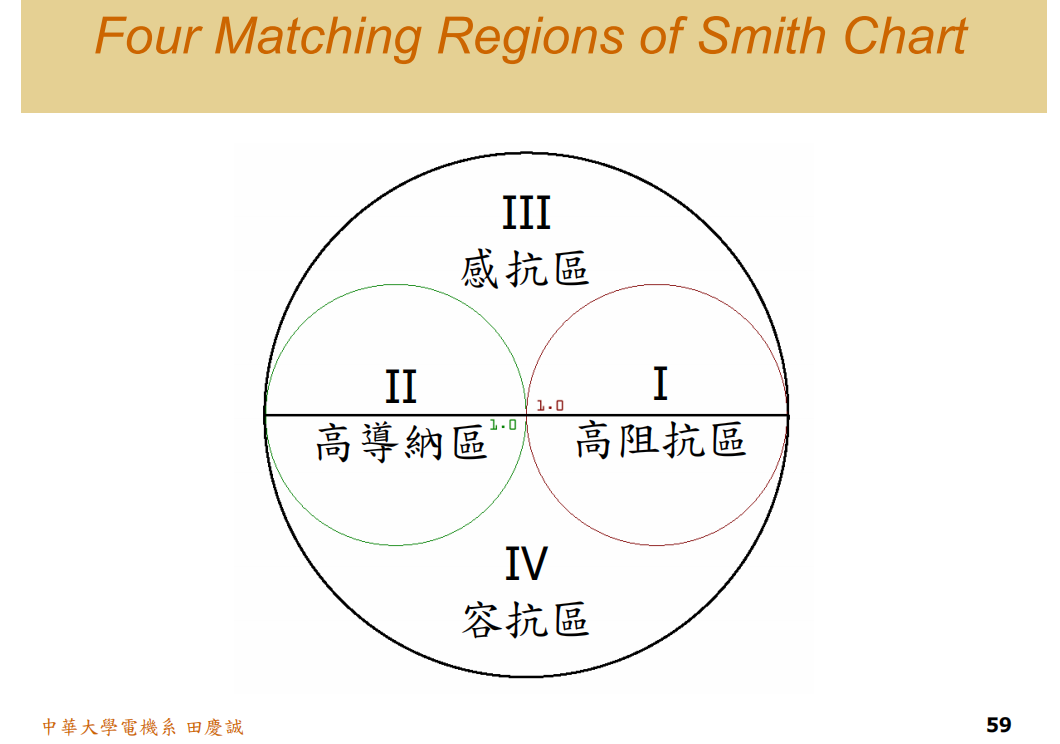
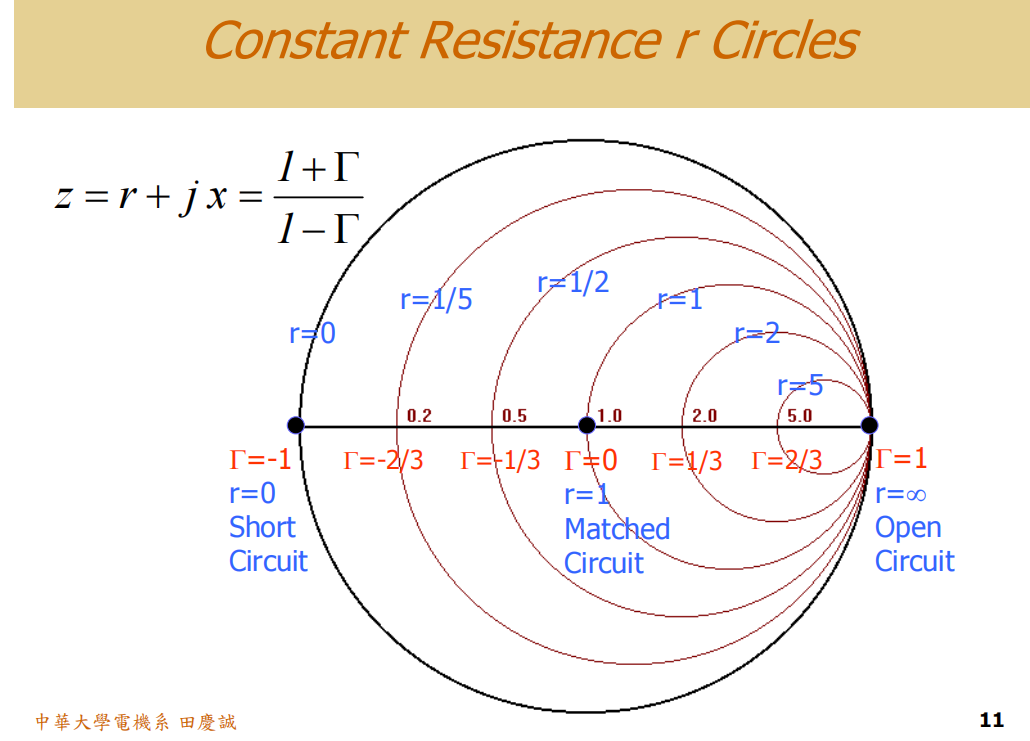
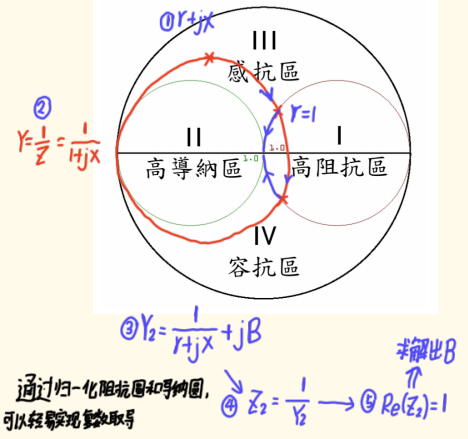
四个区域

史密斯圆图可分为四个区域（感抗区和容抗区等）

每个区域都至少可用两种L型网络进行阻抗匹配，具体分为：

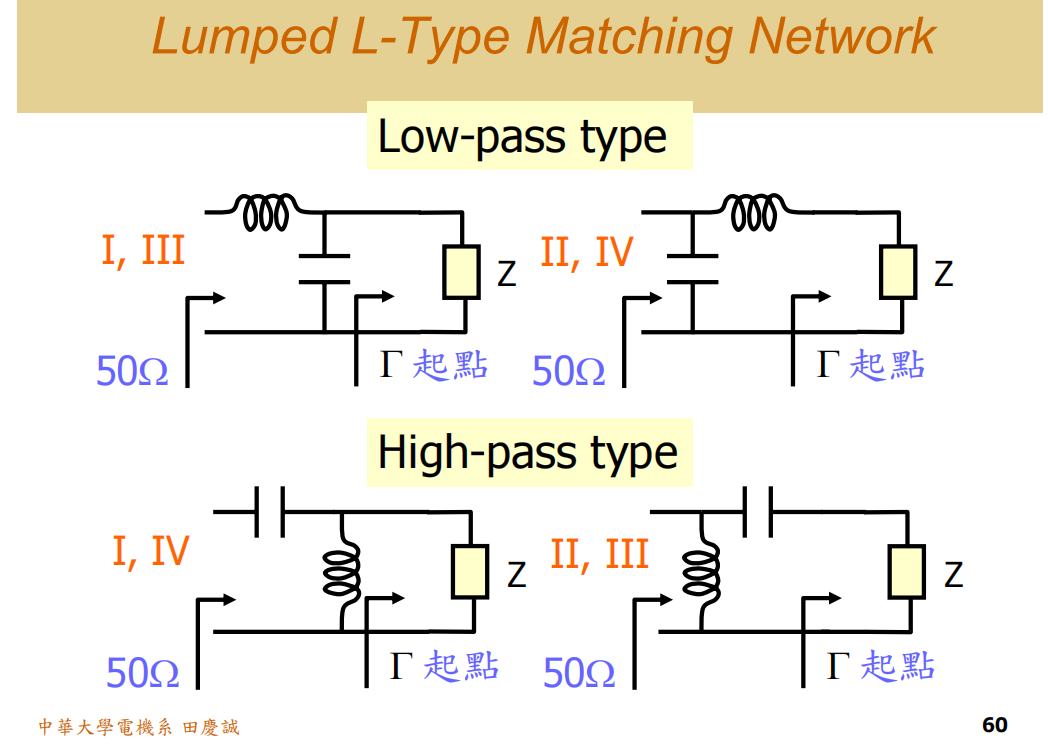
感抗区(三区)：感抗成分较强，可用两个电容（并联+串联）等组合实现匹配，共有四种拓扑结构------包括低通（Low-Pass）、高通（High-Pass）及两种带通（Bandpass）结构。
容抗区(四区)：容抗成分较强，可用两个电感（并联+串联）等组合实现匹配，同样有低通、高通及两种带通结构。
高阻抗区(一区)：只有低通和高通两种结构
高导纳区(二区)：也只有低通和高通两种结构

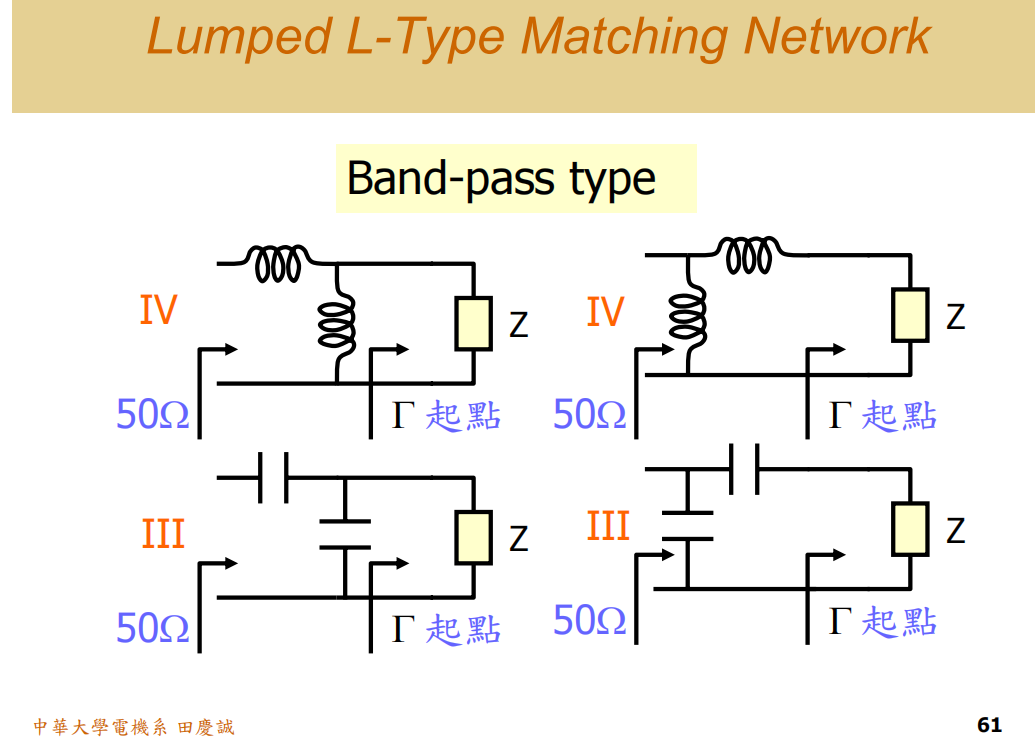
总结规律：

所有区域都至少包含一种低通和一种高通结构；
带通结构仅存在于感抗区和容抗区，每区各有两种。

具体到匹配网络的类型，其覆盖范围与特点如下：

低通（Low-Pass）型：其两种基本电路结构（如串联电感-并联电容，或并联电容-串联电感）可覆盖所有四个阻抗区域，是实现匹配的通用选择。
高通（High-Pass）型：与低通型类似，其两种基本结构也同样能够覆盖全部四个区域。
带通（Bandpass）型 ：此类结构具有明显的区域限制------仅适用于第三区（感抗区） 。其核心优势在于，当阻抗点位于强感性区域时，可以仅使用两个电容 （例如并联电容结合串联电容）便实现完美匹配，构成纯容性匹配网络。
这一点在工程实践中意义显著 ：由于电容通常比电感成本更低，且更容易获得高的品质因数（Q值），因此这种"无电感"方案既能节约成本，又能降低损耗、提升性能。

相比之下，如果阻抗点落在第四区（容抗区），则必须使用两个电感来实现类似结构的匹配，其损耗往往更大，并非理想选择 。

因此，在设计时若能使阻抗点落入感抗区，将更有利于实现高效、经济的带通型匹配。

设计范例与仿真

接下来我们直接看一个匹配电路设计的例子。

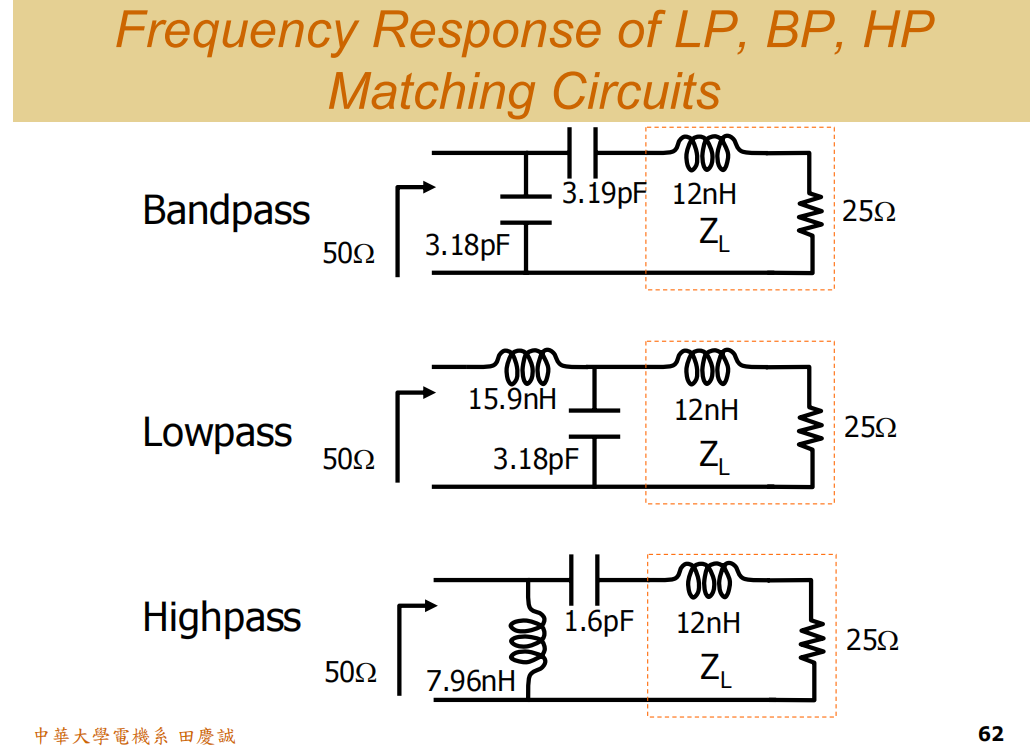
这个范例的阻抗点是落在第几区？我的源阻抗是50欧姆，频率在1GHz，要匹配到的负载阻抗是j75+25Ω。

这个串联阻抗，电阻部分R=25。归一化电阻值为R/50=0.5，所以反射系数的实部大约是-1/3。

感抗部分j75，j50在这个位置，j100大概在这，所以j75应该大约在这个区域。

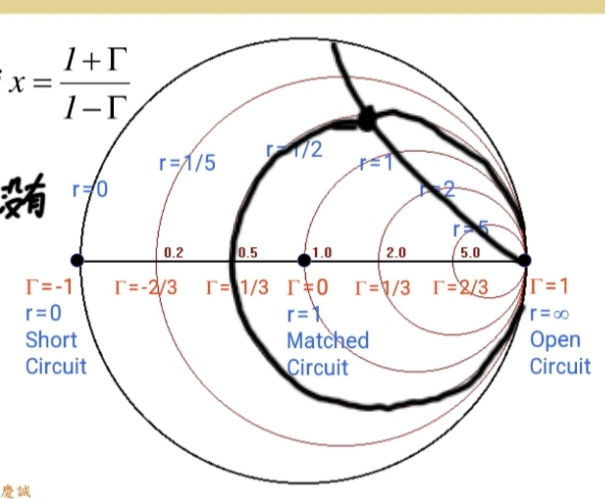
大家看到了吗？所以我们设计这个阻抗点是落在第三区 （感抗区）。

第三区应该有4种电路可选：两种Bandpass，一种Low-Pass，一种High-Pass。

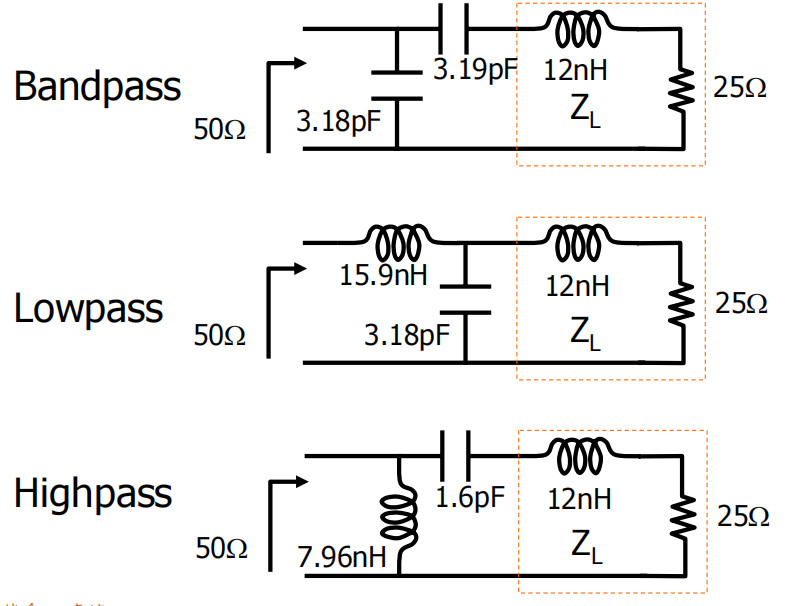
我们再复习一下怎么看它是Low-Pass还是High-Pass：

关键核心就是:看直流（DC）能不能通过。

拿第二个Low Pass电路举例子

串联电感，DC能过（短路），这是Low-Pass元件。

并联电容，DC不能过（开路），电流全通过，所以这也是Low-Pass元件。

所以，一个串联电感加一个并联电容的组合，一个元件让DC过，一个不让过，结合起来就构成了低通（Low-Pass） 特性。

再看第一个Band Pass电路，两个都是电容的网络（串联C+并联C）

对于第一个并联电容，DC都过不去（开路），直接流向负载，这是Low-Pass；对于第二个串联电容，DC过不去，这是High-Pass

一个低通元件＋一个高通元件，两者组合构成了Band-Pass电路

第三个HighPass电路也是如此

对于第一个并联电感，DC能通过，直接被导向地，所以这是High-Pass元件

对于串联电容，DC不能通过，所以也是High-Pass元件，所以两个元件都属于High-Pass特性，这是一个High-Pass电路

来看仿真结果。频率响应可以看到什么现象？

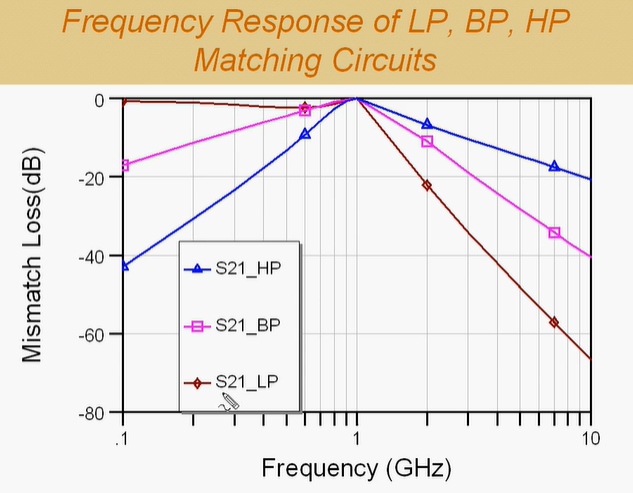
图中纵坐标为匹配损耗，横坐标为频率

匹配损耗（Match Loss）怎么仿真计算？
- 通常我们看反射系数 S11S_{11}S11。
- 实际上，传输到负载的功率比例是 1−∣S11∣21 - |S_{11}|²1−∣S11∣2。
- 匹配损耗（以dB表示）：10∗log10(1−∣S11∣2)10 * log_{10}(1 - |S_{11}|²)10∗log10(1−∣S11∣2) (没有加负号)。这个值越小，说明匹配越好，损耗越低。(比如S11S_{11}S11为0时，表示完全匹配，对于匹配损耗为0dB),在电路仿真软件里，通常可以直接绘制这个公式的结果来评估匹配效率。

对于Low-Pass电路(图中棕色线)，在低频（接近DC）时信号能通过（衰减小），体现出"低通"特性；在目标频率（如1GHz）附近有一个匹配好的通带。

我们知道它低频会通过，那高频呢？哇，衰减得这么厉害吗？

我们来检验一下：当频率增加十倍（即一个Decade，十倍频程）时，看信号衰减了多少。大概在60dB左右(从1Ghz到10Ghz)。

所以，它在高频段每个十倍频程大约会衰减60dB 。

等等，这不是Low-Pass网络吗？

理论上，一个真正的二元件Low-Pass网络（比如串联电感并联电容），每个元件可以提供大约-20 dB/decade的衰减斜率，那么两个元件组合最多是-40 dB/decade才对。为什么这里是-60 dB/decade呢？

答案是：因为它所驱动的负载本身，在高频下也呈现出类似Low-Pass的特性 。

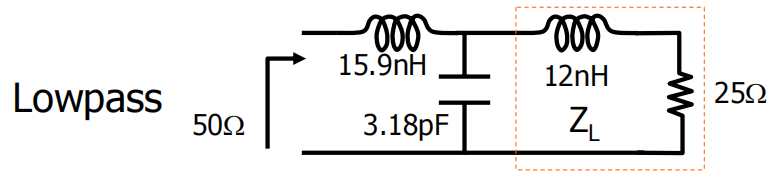
看到了吗？负载部分多了一个Low-Pass特性的元件(DC能通过电感)。

所以总共几个？一开始的匹配网络有两个元件（串L并C），加上负载的一个（电感），总共是三个。三个具有Low-Pass特性的元件串联，高频衰减斜率就是大约 -20 x 3 = -60 dB/decade。

我们再来看Bandpass（带通）网络。它由一个Low-Pass元件和一个High-Pass元件组成，对不对？现在再加上负载那个Low-Pass元件。

在高频段 ：匹配网络中的Low-Pass元件（-20）和负载的Low-Pass元件（-20）共同作用，所以斜率是 -40 dB/decade。
在低频段 ：匹配网络中的High-Pass元件（-20）起主要作用，斜率是 -20 dB/decade。

然后是High-Pass（高通）网络。这个例子中，匹配网络的两个元件都是High-Pass特性，但负载仍是Low-Pass特性。

在高频段 ：负载的Low-Pass元件（-20）起作用，斜率是 -20 dB/decade。
在低频段 ：匹配网络的两个High-Pass元件（每个-20）共同作用，斜率是 -40 dB/decade。

这样会估算了吗？电路做出来后，你大致就能估算它的频率响应了。比如，你想滤除谐波（Harmonics），一个极点（一阶衰减）在二倍频处能衰减多少？

注意，这里的-20 dB/decade是针对十倍频程的。那对于二倍频（Octave，两倍频程），一个极点大约衰减6dB。所以一个极点：-6dB；两个极点：-12dB；三个极点：-18dB......

这个估算在频率偏移较远时比较准，越靠近中心频率误差会大一些 。所以，你大概能知道你的电路能抑制多少谐波。

以这个例子来看，大概能抑制掉20dB的谐波。

这就是为什么在设计功率放大器（Power Amplifier）时，匹配网络尽量采用Low-Pass结构，它可以有效抑制谐波 。

如果你用其他结构，可能抑制效果就没那么好。当然，前提是你的负载也有Low-Pass特性。如果你的负载没有这个特性，那想抑制谐波就不容易了。

编程任务

任务目标：编写一个程序，自动计算将任意给定负载阻抗匹配到50欧姆所需的所有无耗L型匹配网络解及其元件值。

输入：

负载阻抗的实部 R 和虚部 X（即Zload=R+jXZ_{load} = R + jXZload=R+jX）。
参考阻抗Z0Z_0Z0（默认为50欧姆）。
工作频率 f。

输出：

所有可能的L型匹配电路拓扑。
每个拓扑对应的电感L和电容C的具体数值。

有同学会按照我上课讲的方法，先判断负载点落在史密斯圆图的哪个区域（第一、二区有两个解，第三、四区有四个解），然后分情况计算。但这样编程会非常繁琐，代码又长又复杂。

其实，我们不需要关心它在哪个区域。对于程序来说，L型匹配只有两种基本拓扑结构：

拓扑A：先并联（shunt），再串联（series）。
拓扑B：先串联（series），再并联（shunt）。

我们只需要对这两种拓扑分别求解。有些情况下可能无解，程序需要能判断。

先并联，后串联

以"先并联，再串联"（拓扑A）为例

假设负载点ZloadZ_{load}Zload 在圆图上对应点 A。

第1步：从并联开始

我们要在负载上并联一个电抗（电感或电容）。在圆图上，并联操作意味着负载点将沿着等电导圆constant conductance circle移动。

程序如何实现？

将负载阻抗 Zload(R+jX)Z_{load} (R + jX)Zload(R+jX) 转换为导纳 Yload=G+jBY_{load} = G + jBYload=G+jB。这在程序中就是计算复数倒数：Yload=1/ZloadY_{load} = 1 / Z_{load}Yload=1/Zload。
- 这就是史密斯圆图的神奇之处：从"阻抗圆图"视角切换到"导纳圆图"视角，在程序里只是一个简单的复数运算，却对应了图上强大的可视化转换。
并联一个电纳 jBpjB_pjBp 后，新的导纳点为：Y1=Yload+jBpY_1 = Y_{load} + jB_pY1=Yload+jBp。BpB_pBp 可正（并联电容）可负（并联电感），是待求量。

第2步：并联的目标是什么？

我们并联的目的是为了将阻抗（导纳）点调整到一个位置，使得接下来通过串联一个元件就能直达50欧姆点（即圆心Z0Z_0Z0）。

在圆图上，这意味着Y1Y_1Y1点经过串联操作后必须落在Z0Z_0Z0上。串联操作是沿等电阻圆constant resistance circle 移动。
Z0Z_0Z0（50欧姆）归一化后为1+j01 + j01+j0，它所在的等电阻圆就是R=1R=1R=1的圆。
因此，并联的目标是：找到合适的BpB_pBp，使得Y1Y_1Y1转换回阻抗Z1=1/Y1Z_1 = 1 / Y_1Z1=1/Y1后，其归一化实部等于1。

即：Re(Z1/Z0)=1Re(Z_1 / Z_0) = 1Re(Z1/Z0)=1或 Re(1/(Y1∗Z0))=1Re(1 / (Y_1 * Z_0)) = 1Re(1/(Y1∗Z0))=1。

第3步：建立方程并求解

将Y1=Yload+jBp=Gload+j(Bload+Bp)Y_1 = Y_{load} + jB_p = G_{load} + j(B_{load}+ B_p)Y1=Yload+jBp=Gload+j(Bload+Bp) 代入方程Re(1/Y1)=Z0Re(1 / Y_1) = Z_0Re(1/Y1)=Z0（这里假设Z0=1，使用归一化值）。

展开并令其实部等于1，可以得到一个关于未知数BpB_pBp的二次方程：
(Gload)2+(Bload+Bp)2=Gload(G_{load})^2 + (B_{load} + B_p)^2 = G_{load}(Gload)2+(Bload+Bp)2=Gload

求解这个二次方程，一般会得到两个解：Bp1B_{p1}Bp1 和 Bp2B_{p2}Bp2。这对应了在等电导圆上移动时，能到达R=1圆上的两个交点。

第4步：确定并联元件类型和值

根据解出的BpB_pBp：

如果BpB_pBp > 0，表示需要并联一个电容，其值 C = BpB_pBp / (2πf)。
如果BpB_pBp < 0，表示需要并联一个电感，其值 L = -1 / (2πf * BpB_pBp)。

第5步：计算串联元件

对于每个求得的Y1Y_1Y1（或对应的Z1Z_1Z1）点，我们现在需要串联一个电抗 jXsjX_sjXs，使总阻抗变为Z0Z_0Z0。

即：Z1+jXs=Z0Z_1 + jX_s = Z_0Z1+jXs=Z0

所以，jXs=Z0−Z1jX_s = Z0 - Z1jXs=Z0−Z1。计算 XsX_sXs：

如果 Xs>0X_s > 0Xs>0，需要串联一个电感，L=Xs/(2πf)L = X_s / (2πf)L=Xs/(2πf)。
如果 Xs<0X_s < 0Xs<0，需要串联一个电容，C=−1/(2πf∗Xs)C = -1 / (2πf * X_s)C=−1/(2πf∗Xs)。

这样，对于"先并后串"拓扑，我们最多得到两组解 （因为BpB_pBp有两个解）。

先串联，再并联的思路完全对称：

从负载阻抗ZloadZ_loadZload开始，串联一个电抗jXsjX_sjXs，得到Z1=Zload+jXsZ1 = Z_load + jX_sZ1=Zload+jXs。这一步沿等电阻圆移动。
串联的目标是：使Z1Z_1Z1转换成的导纳Y1=1/Z1Y_1 = 1 / Z_1Y1=1/Z1，其归一化实部等于1（即位于G=1G=1G=1的等电导圆上）。这样接下来并联一个元件就能到圆心。
建立方程Re(1/Z1)=1Re(1 / Z_1) = 1Re(1/Z1)=1，求解关于XsX_sXs的二次方程，得到两个解。
确定串联元件是电感还是电容。
对每个Z1Z1Z1，计算需要并联的电纳jBp=Y0−Y1jB_p = Y_0 - Y_1jBp=Y0−Y1，并确定并联元件是电感还是电容。

同样，最多可得到两组解。

总结与输出

综合以上两种拓扑，程序最多可输出4组解 （两组来自拓扑A，两组来自拓扑B）。这与我们根据区域判断的结论（第三、四区有4个解）是一致的。对于第一、二区，有些解可能因为元件值为负或无实数解而无效，程序应能自动过滤。
编程核心 ：就是围绕上述两个方程进行复数运算和二次方程求解。不需要在代码里手动判断区域、画圆或枚举所有LC排列。

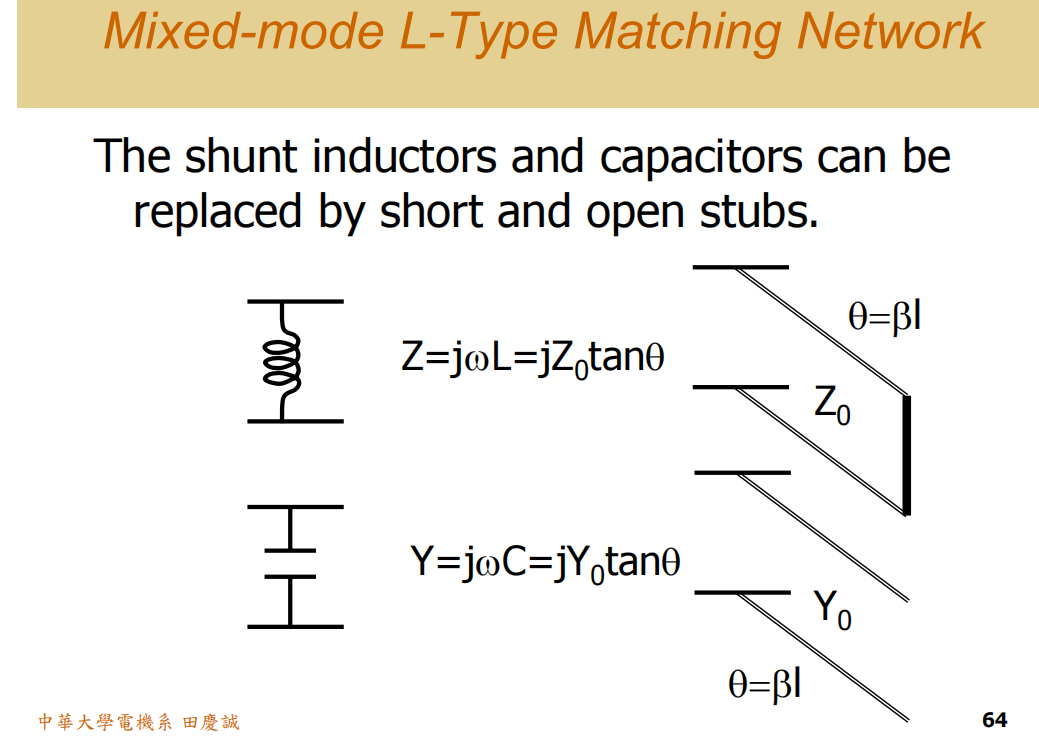
传输线实现L型网络

我们之前教的都是纯集总参数电路（Lumped Circuit）。但现实中，比如一个集总电感，你可以用一段终端短路的传输线（Short Stub）来等效替代；一个集总电容，可以用一段终端开路的传输线（Open Stub）来等效替代。

那么电路板（PCB）上怎么实现呢？来看图：

原来的集总电感（并联接地）：主传输线（火线）上要并联一个电感到地。这就需要打一个过孔（Via）接地。
用短路支线（Short Stub）替代 ：主传输线（火线）分出一个"T"形或支节，这是一段传输线。它的另一端（终端）必须通过过孔（Via）连接到下层的地平面。
为什么它等效为电感？
根据传输线理论，从输入端看进去的阻抗是 jZ0∗tan(βl)jZ_0 * tan(βl)jZ0∗tan(βl) 。当长度 l 小于四分之一波长（即电长度 θ=βl < 90°）时，阻抗呈感性。物理上可以理解为：电流波传播到短路端反射，形成驻波，输入端呈现感性电抗。切记：长度必须小于λ/4，否则会变成容性。
用开路支线（Open Stub）替代电容 ：这个更容易。从主传输线引出一段支线，末端什么都不接（悬空） ，这就是开路支线。它等效为一个接地电容。我强烈建议，对于小的并联电容，尽量用开路支线来替代。
为什么？因为省去了一个过孔和一个实体电容元件，既省钱（一个电容和过孔都要成本）又便于调试（用刀片刮一下就能微调长度）。但是，如果你需要很大的接地电容（比如射频扼流圈的大旁路电容），想用λ/4开路支线来等效（此时阻抗接近0，相当于短路），那需要的物理长度会很长，很不划算，这种情况下还是直接用集总电容更实际。

制作时的两个重要注意事项：

过孔（Via）的电感效应 ：一个直径0.6mm的过孔，其寄生电感大约为0.15 nH（具体值需根据板厚等参数计算）。既然已经有这个小电感了，你用来替代集总电感的短路支线（Short Stub）的实际长度应该比理论计算值缩短一些，因为总电感是支线等效电感和过孔寄生电感之和。
开路端（Open End）的电容效应 ：开路支线的末端与地平面之间会存在边缘场，产生一个小的寄生电容。这个电容与你设计的支线等效电容是并联的。
因此，为了达到目标电容值，开路支线的实际长度也应该比理论值略微缩短一点。

四分之一波长阻抗变换器

假设我有一个阻抗Z1Z_1Z1，要匹配到Z2Z_2Z2。我可以让Z1Z_1Z1沿着一段传输线"向源端移动"（即在史密斯圆图上沿等驻波系数圆旋转）。

公式是：Γ2=Γ1∗e−j2βlΓ₂ = Γ₁ * e^{-j2βl}Γ2=Γ1∗e−j2βl，其中相位变化由 2βl 决定。

β是多少？β=2π/λ，它与频率成正比（因为光速固定）。

所以频率越高，β越大，在圆图上旋转的角度就越大 。

我们需要旋转多少角度？从Γ₁所在的角度，旋转到Γ₂所在的角度。

注意：旋转的角度差是 2θ，其中 θ=βl 是传输线的电长度。 旋转时，半径（反射系数模值）不变。

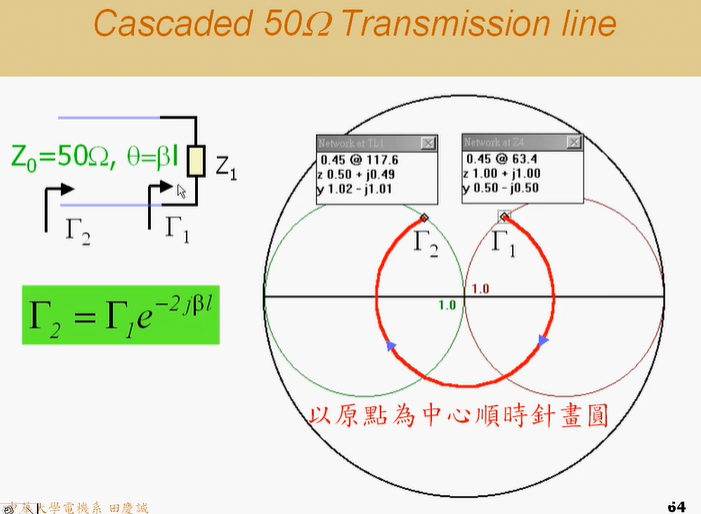
我们来练习一下：如果传输线长度 l = λ/4 （即θ= βl =90°），那么阻抗点会转到圆图上哪个位置？

答案：它会走到史密斯圆图上对角的位置（即直径的另一端）。这个位置对应的阻抗是多少？如果Z1是某个值，那么变换后的阻抗ZIN=Z02/ZLZ_{IN} = Z_0² / Z_LZIN=Z02/ZL（其中Z0是传输线的特性阻抗）。

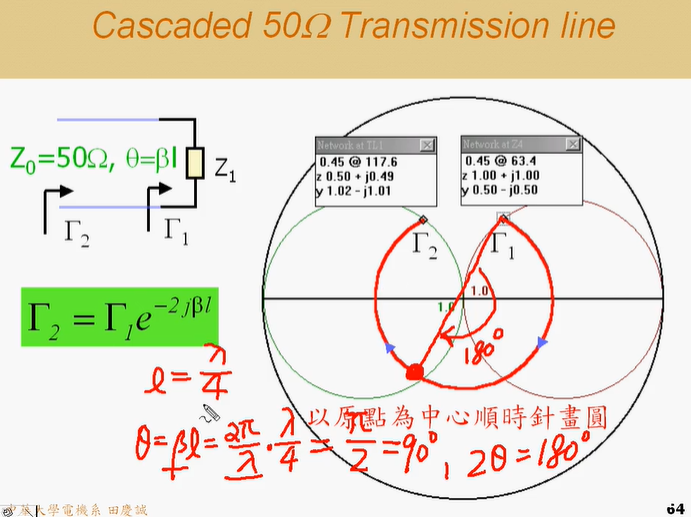
这被称为四分之一波长阻抗变换器 （Quarter-wave Impedance Transformer或Impedance Inverter），因为它将阻抗"倒置"了。

单用一段50欧姆传输线来进行匹配，通常不够灵活（因为它只能在等反射系数圆上移动，无法到达任意点）。

所以，50欧姆传输线常常需要配合并联或串联的集总元件（或支线） 一起使用，构成更灵活的匹配网络。这也是L型匹配网络的一种变体。

50欧姆传输线的匹配方法

因为50欧姆线的宽度通常适中，既不太宽也不太窄，很实用。我们常常配合50欧姆线来设计。
案例1：从Γ1Γ_1Γ1匹配到50欧姆

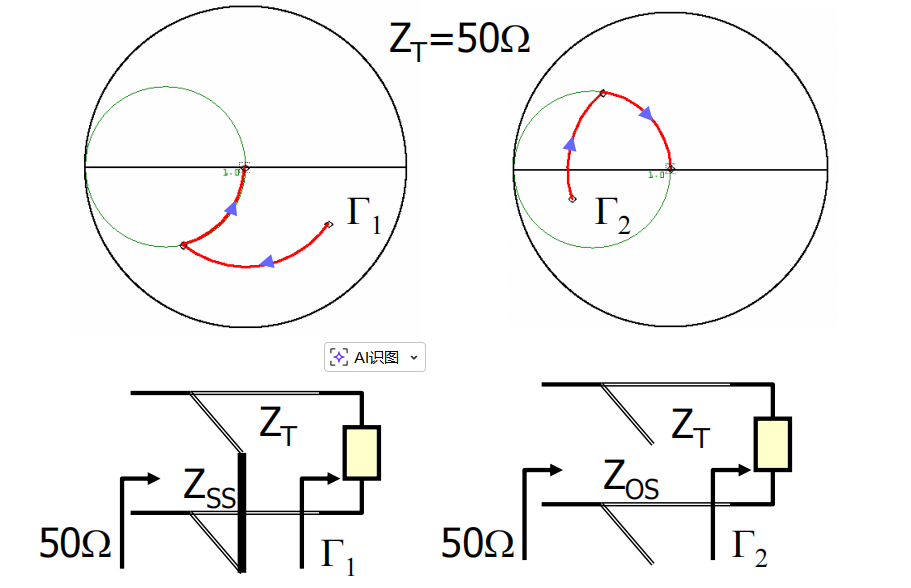
比如，我有一个源阻抗在Γ1Γ_1Γ1点，想匹配到50欧姆中心点。怎么做呢？我可以先串联一段50欧姆传输线 。注意，在史密斯圆图上，这是沿等反射系数圆顺时针（向源端）旋转 。（顺源逆载）

当旋转到与等电导圆（绿色）相交时，我们就可以在这个位置并联一个元件 （比如电感）到地。这个并联电感可以用一个短路支线 来替代，既省钱效果又好。

那么实际电路怎么实现呢？

从源端（Z1）先接一段50欧姆主线，然后在这里分出一个短路支线（T型结构），终端打过孔接地。这样，一段传输线加一个短路支线就构成了匹配网络。
案例2：从Γ2Γ_2Γ2匹配到50欧姆

同理，如果起始点在Γ2Γ_2Γ2，我也先串联一段50欧姆线，顺时针旋转到与等电导圆相交。这次需要并联的是电容到地。这个并联电容可以用一个开路支线 来替代，连过孔都省了，直接悬空末端即可。这是最省成本的做法，在PCB上走线就能实现。
这种方法的优势：

成本极低：省去了昂贵的集总电感和电容，尤其是小值元件。
易于调试：用刀片刮一下微调支线长度，就能改变等效感抗或容抗，调试非常方便。

当然，也要考虑面积。如果板子空间非常紧张，用长传输线可能反而浪费面积，这时用集总元件可能更紧凑。但对于很小的电感或电容，用短支线替代通常非常划算，既省成本又便调试。
高级技巧：可调电容阵列

此外，为了实现可调（Tuning），你可以这样做：在主线附近预留一些小金属方块 。需要增加电容时，用焊锡将方块与主线连接，这就形成了一个小的开路支线。你可以在不同位置预留多个方块，通过焊接不同组合来并联多个小电容，从而改变总电容值。

这就像一个分布式的可调电容阵列，可以节省面积并增加设计灵活性。但要注意，连接点（T型或十字型结）的寄生效应需要计算进去。

非50欧姆传输线的单线匹配法

那么，我可以不用50欧姆线，只用一段特殊阻抗的传输线就完成匹配吗？

可以，但情况有所不同。

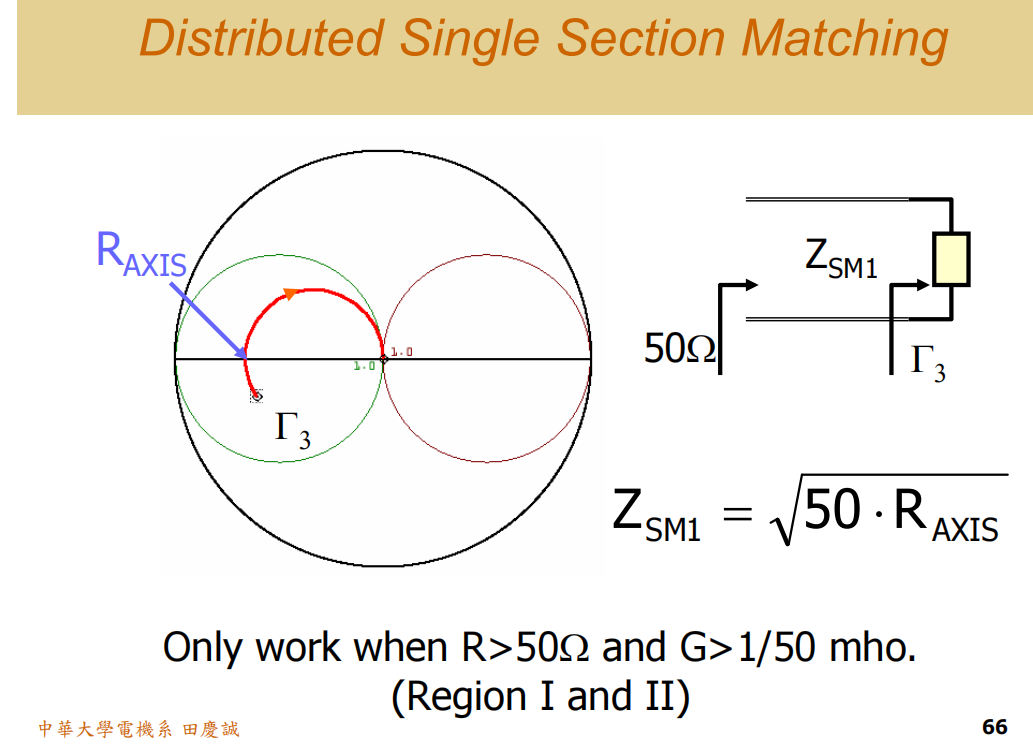
假设起始点在Γ3Γ_3Γ3。我串联一段特性阻抗为ZSM1Z_{SM1}ZSM1（非50Ω）的传输线。在史密斯圆图上，它会围绕一个新的圆心（不再是原点）沿等反射系数圆顺时针旋转 。

这个圆的特征是会同时经过原点（50Ω点）和起始点Γ3Γ_3Γ3 ，并且图形是上下对称的。
如何确定这段线的阻抗和长度？

理论上，你可以用圆规画一个同时通过50Ω点和Γ3Γ_3Γ3点，且上下对称的圆。这个圆会与实数轴（水平轴）相切于一点，设该点对应的归一化阻抗为r 。

根据四分之一波长阻抗变换器 原理，当线长正好为λ/4时，阻抗会变换到圆上对称的另一端。因此，这段传输线的特性阻抗Z0可以通过公式估算：ZSM1≈RAXIS∗50Z_{SM1} ≈\sqrt{R_{AXIS} * 50}ZSM1≈RAXIS∗50 。

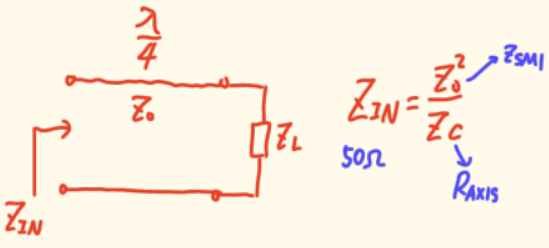
实际上，这个圆的圆心点阻抗与Z0非常接近，但不完全相等。你可以先用圆心阻抗值作为初始估计，再进行微调。
例子：假设Γ3Γ_3Γ3的反射系数约为 -2/3，对应阻抗约为0.2（归一化值，即R = 10Ω）。画出的对称圆与实轴切点的r值大约为0.5（即25Ω）。

那么传输线特性阻抗ZSM1≈RAXIS∗50Z_{SM1} ≈\sqrt{R_{AXIS} * 50}ZSM1≈RAXIS∗50 ≈ 50 * √0.2 ≈ 22.4Ω。而圆心阻抗约25Ω(0.5*50)，两者确实很接近。所以调试时，可以先按接近圆心阻抗的值来选线宽，再微调长度。

重要限制与缺点：

仅适用于特定区域 ：这种单线匹配法通常只适用于第一区或第二区（阻抗点落在实轴附近或高阻/低阻区）。对于第三、第四区（强感性或强容性），你很难画出一个同时经过50Ω点和该点且上下对称的圆，因此无法用单一线段完成匹配。
线长可能很长 ：为了实现所需的阻抗变换，旋转的角度可能很大，导致需要的传输线物理长度很长，可能超过λ/4。
耦合与寄生效应 ：当线很长且靠近其他走线或地平面时，会产生寄生耦合。电磁波会"抄近路"，导致等效电长度缩短，实际效果偏离理论计算。同时，这种耦合也会破坏理想的圆形旋转轨迹，增加设计复杂度。

因此，除非所需线段很短，否则一般不建议使用这种单段非50Ω线匹配法。当需要长线时，还是更推荐结合并联支线（L型网络）的方法。

当然，这种非50欧姆传输线也可以配合并联支线一起使用，构成更复杂的匹配网络

举个例子：如果你的阻抗点无法通过单段50欧姆传输线直接匹配到中心（因为旋转角度太长）

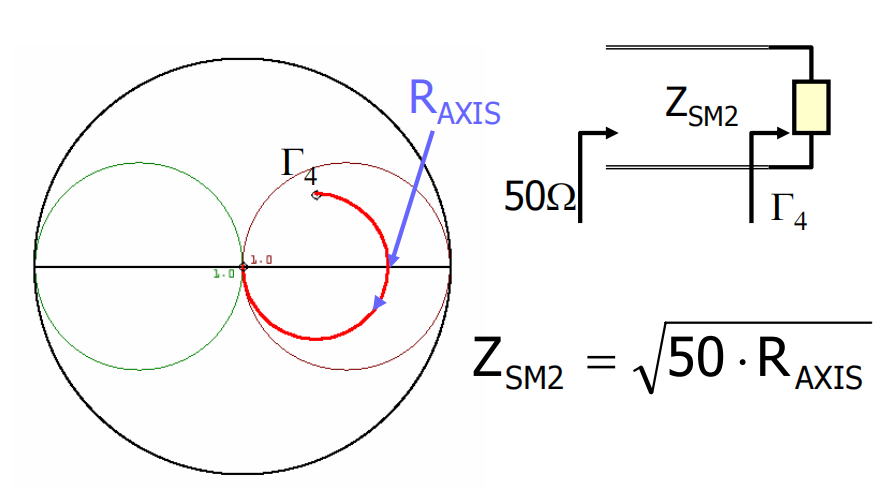
可以先用一段特定阻抗的传输线，将阻抗点转到靠近某个等电导圆的位置，然后再并联支线完成匹配。

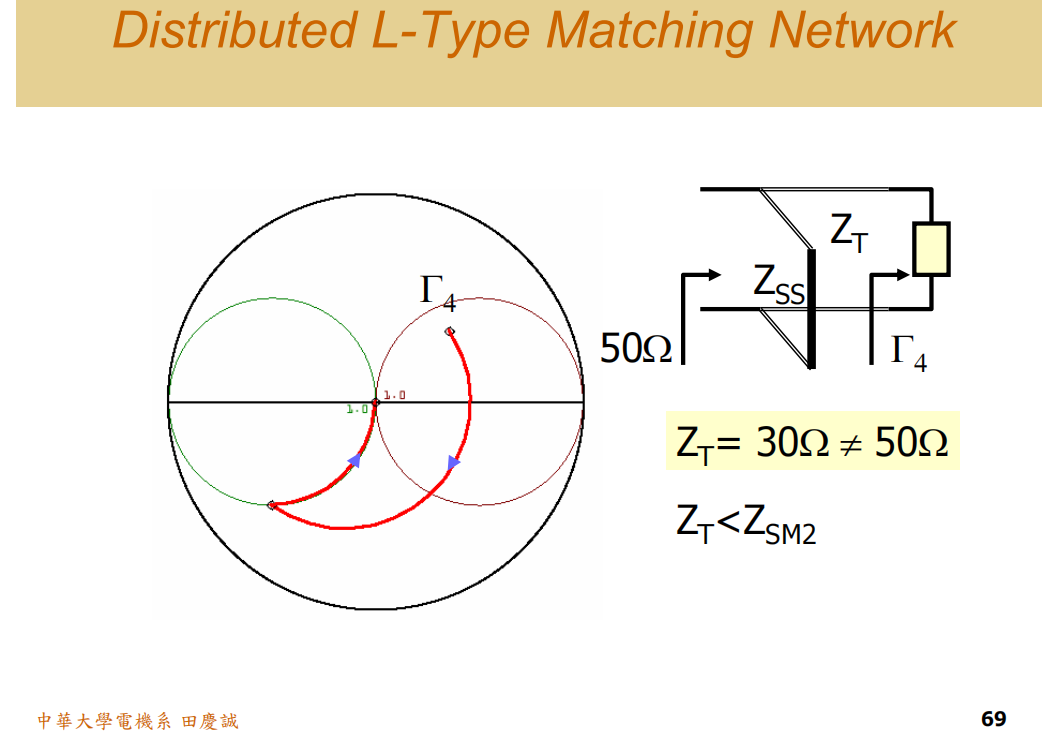
所以，有时候为了缩短传输线长度、优化布局，中间这段线的阻抗不一定要是50欧姆。这种不同特性阻抗传输线的组合运用，就交给大家灵活掌握了。

阻抗的Q值（Impedance Q）

这里的Q值与电路学中电感、电容的Q值完全不同 。它特指匹配电路中，待匹配负载的Q值。

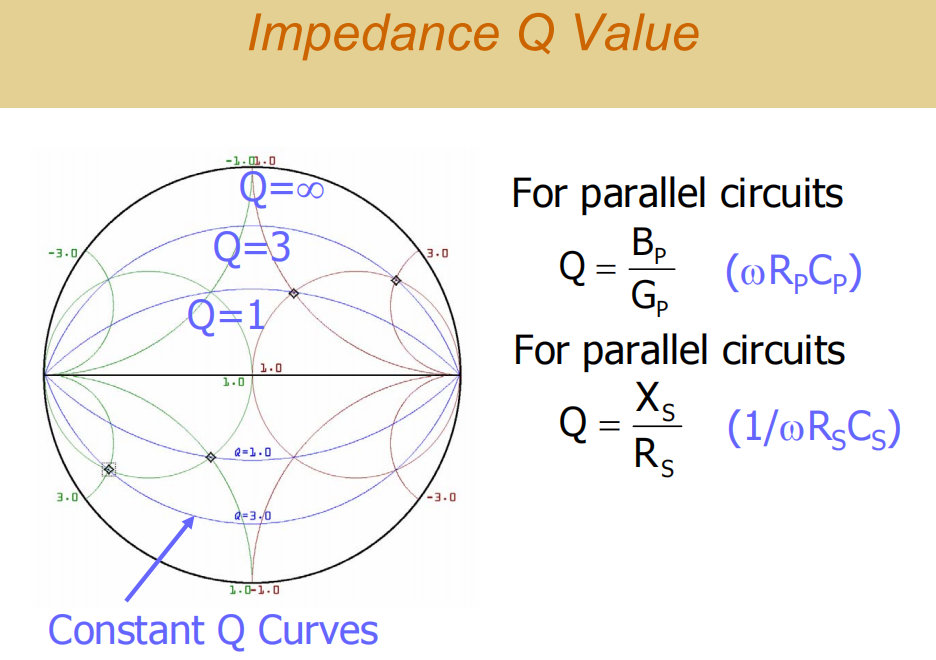
定义：对于任何一个复阻抗负载Z = R + jX（串联形式），我们定义其Q值为 |X| / R 。

对于导纳形式 Y = G + jB（并联形式），则定义其Q值为 |B| / G 。
对于同一个阻抗点，用串联或并联形式计算出的Q值是相等的。

在史密斯圆图上的体现 ：这些等Q值轨迹在圆图上是一簇弧线。图中画出了几条：

最内侧的弧线是 Q=1 的轨迹。在这条线上，任意一点的 |X|/R 或 |B|/G 都等于1。
外面一条大约是 Q=3 的轨迹。
我们可以把圆图大致按Q值划分为三块区域：Q在0 ~ 1之间，1~3之间，以及大于3。

示例：

假设在某频率下，一个负载可等效为电阻Rp，并联电容Cp。

则其导纳 Y = 1/Rp + jωCp，所以 Q = ωCp / (1/Rp) = ωCpRp 。

如果我们将同一点负载等效为电阻Rs，串联电容Cs

（注意：Rp≠Rs，Cp≠Cs）。

则其阻抗 Z = Rs + 1/(jωCs)，所以 Q = |1/(ωCs)| / Rs = 1/(ωCsRs)。

Bode-Fano准则（Bode-Fano Criterion）

理解了这个Q值之后，我们要引入一个非常重要的理论------波德-法诺准则 。它有点数学化，但至关重要，能让你避免掉进"不可能完成的任务"这个坑。

这个理论说的是：对于一个给定的复阻抗负载 （比如Rp并联Cp，或Rs串联Ls），当你使用无耗匹配网络时，其反射系数Γ(ω)在整个频带内的表现有一个物理极限 。

公式给出了一个积分上限：
∫0∞ln1∣Γ(ω)∣dω≤πω0Q∫₀^∞ ln\frac{1}{|Γ(ω)|} dω ≤ \frac{π ω₀}{Q}∫0∞ln∣Γ(ω)∣1dω≤Qπω0

其中：

ω₀是中心频率。
Q就是刚才定义的负载的Q值（例如，对于Rp//Cp负载，Q = ω₀ Rp Cp）。

这个不等式的物理意义非常深刻：

理想匹配与带宽的矛盾：等式左边是反射系数倒数对数的积分。要获得"好"的匹配（即小的|Γ|），我们希望 ln(1/|Γ|) 尽可能大；要获得"宽"的带宽，我们希望这个"好"的状态在很宽的频率范围（dω）内都成立。但积分总值受到右边上限的限制。
Q值的关键作用 ：上限值反比于负载的Q值。负载的Q值越高 （即电抗成分相对于电阻成分越大，匹配难度越大），这个上限值越小。
这意味着，对于一个高Q值的负载(上限已经被定死)，你绝对不可能 同时实现极低的反射系数（完美匹配） 和极宽的带宽。你只能在这两者之间进行权衡：要么牺牲带宽换取更好的匹配深度，要么放宽匹配要求来获取更宽的带宽。

如果你老板（或客户）给你一个指标：要求在某中心频率附近一个很宽的频带内，反射系数都要低于一个非常苛刻的值（比如-30dB）。

你最好先算出负载在这个频段的Q值，然后代入波德-法诺准则算一下积分上限。

如果理论上的积分上限远远小于实现这个指标所需的积分值，那么这个指标在物理上就是不可能实现的 。这时候你就不是能力问题，而是物理定律不允许。你可以用这个准则有理有据地向老板说明，避免去做无用功，或者重新协商一个合理的指标。

所以，大家一定要理解并记住这个准则，它是评估宽带匹配电路理论性能极限的利器。

好的，我们接着下结论。

结论1：宽带匹配的权衡

根据波德-法诺准则，串联负载的结论也是一样的，性能上限与 1/Q 成正比，与Q成反比。

因此，如果你想做宽带匹配 ，在给定的负载Q值下，唯一的可能就是放宽对反射系数的要求。你不能要求在整个频带内反射系数都非常好（比如-20dB以下）。很多同学在实践中会发现，如果把指标放松到例如 -7 或 -8 dB，确实可以做出更宽的带宽。这就对了！因为物理上限制了你无法同时实现"匹配极好"和"极宽"。

结论2：理想匹配点的有限性

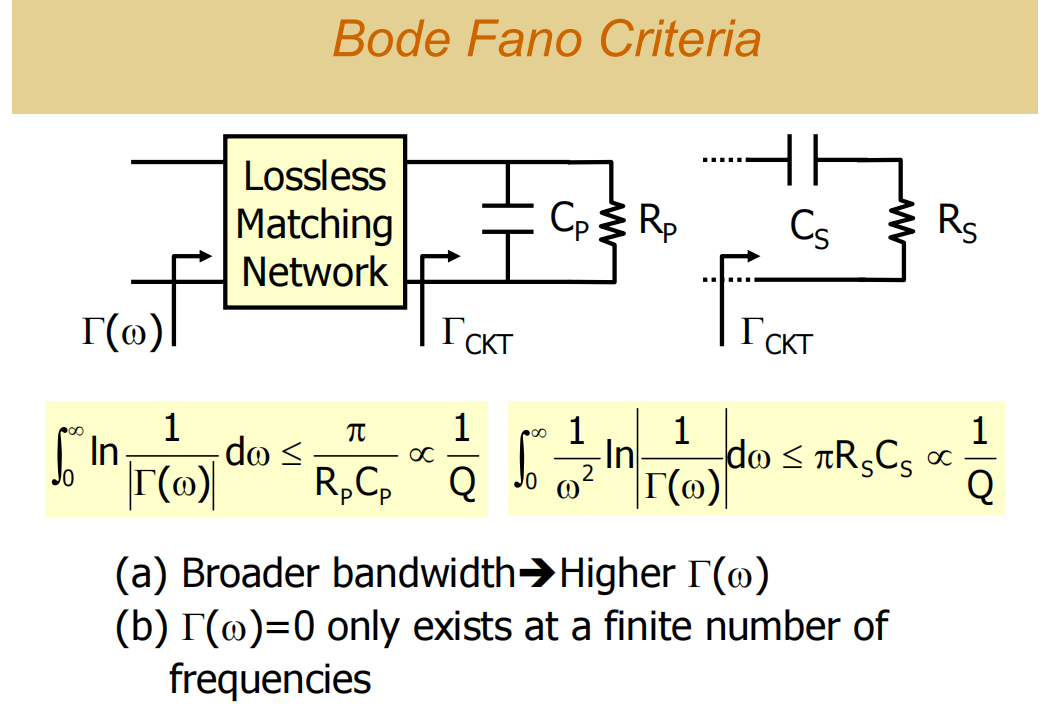
从准则还能推出另一个结论：你不可能 在一个连续的频带内，让反射系数处处为零（完美匹配）。如果那样，积分值将趋于无穷大，这违反了不等式。

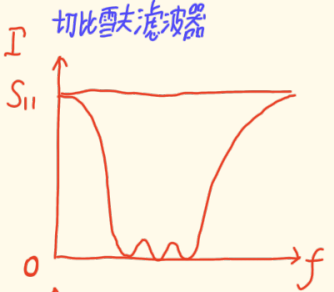
唯一可能的是，在有限的几个离散频率点 上实现反射系数为零（完美匹配）。这正是我们熟悉的滤波器响应：比如一个带通滤波器，其反射系数S11在阻带接近1（全反射），只在通带内有限的谐振点处达到零（如图中几个"凹陷"的谷底）。

结论3：宽带匹配响应的可能形态

那么，一个宽带匹配电路的反射系数响应可能是什么样子呢？通常有两种思路：

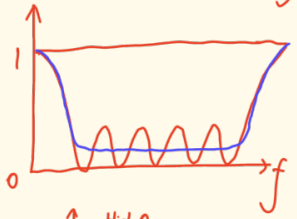
牺牲匹配深度换取带宽：响应曲线可能比较"平缓"，在整个目标频带内反射系数都维持在某个"尚可"的水平（比如 -10 dB），但不会出现极深的零点。这样带宽可以很宽。
允许几个匹配零点，但整体抬高水平：响应曲线可能在几个频率点有很深的匹配（反射系数接近0），但为了拓宽整体带宽，这些零点之间的区域反射系数会相对较高，形成一个"波浪形"但整体覆盖较宽的曲线。

设计评估方法 ：

在实际设计前，你可以用波德-法诺准则快速估算。假设目标是在带宽 Δω 内，反射系数大致为常数 |Γ|，那么不等式简化为：
Δω∗ln1∣Γ∣≤πω0QΔω * ln\frac{1}{|Γ|} ≤ \frac{π ω₀}{Q}Δω∗ln∣Γ∣1≤Qπω0

这样，给定负载Q值和中心频率ω₀，你就能估算出在目标带宽Δω下，理论上能达到的最好匹配深度 |Γ| 是多少，或者在目标匹配深度下，理论的最大带宽Δω是多少。如果客户指标远超这个估算值，那在物理上就是不可能完成的任务。

阻抗Q值与史密斯圆图

我们回顾一下，负载的Q值定义为电抗分量与电阻分量的绝对值之比（|X|/R 或 |B|/G）。在史密斯圆图上：

高Q负载 ：对应的点非常靠近外圈单位圆（接近纯电抗）。
低Q负载 ：对应的点靠近中心的实轴。

核心结论：负载Q值越高，实现宽带匹配就越困难，甚至不可能。 如果老板让你用一个高Q负载（比如接近纯电抗的晶体管输出阻抗）去做宽带匹配，且只能用LC无耗元件，这很可能是一个"不可能的任务"。加入电阻可以降低Q值，拓宽带宽，但会引入损耗。

然而，决定最终电路带宽和损耗的，不仅仅是负载的Q值 ，更是匹配网络变换路径上的最大Q值。

关键概念 ：在设计匹配网络时，从源到负载的阻抗变换会在史密斯圆图上形成一条路径。这条路径会经过多个中间阻抗点。我们需要关注的是整条路径上所有阻抗点的Q值。

窄带、高损耗设计：如果匹配路径"绕远路"，中途跑到了圆图外围的高Q区域，那么：
1. 带宽窄：高Q点对频率极其敏感，频率稍有偏移，阻抗变化巨大，导致匹配迅速恶化。
2. 损耗大 ：高Q点意味着电抗成分远大于电阻成分。当实际电感（其本身有串联电阻）工作在这种高Q（即高电抗/低电阻）状态时，其寄生电阻上的损耗比例会显著增加，导致整个匹配网络效率下降。
宽带、低损耗设计 ：理想的宽带低损匹配，其路径应尽可能贴近实轴，保证路径上每一点的Q值都很低。
1. 带宽宽：低Q点对频率不敏感，阻抗变化平缓，有利于拓宽带宽。
2. 损耗低：元件（尤其是电感）工作在其低Q（相对低电抗）状态，其寄生电阻上的损耗占比小，网络整体效率高。

设计准则：为实现宽带匹配，你必须确保匹配网络在史密斯圆图上的整个变换路径，都尽可能地贴近实轴，即保证路径上每一点的阻抗Q值都很低。

这就是为什么在低噪声放大器（LNA）前级和功率放大器（PA）后级等对损耗极其敏感的设计中，教科书和资深工程师都会强调匹配路径要"贴近实轴"。

这样做不仅能最大化带宽，更能最小化匹配网络本身引入的损耗 （我们后续会证明为什么宽带设计损耗更低）。
反之，如果想设计一个窄带、频率选择性强的匹配网络（比如滤波器），就应该刻意让路径远离实轴，经过高Q区域。

L型匹配网络的局限性

L型（两元件）匹配网络的结论：它的Q值在给定源和负载阻抗后是固定的，无法由设计者自由选择。

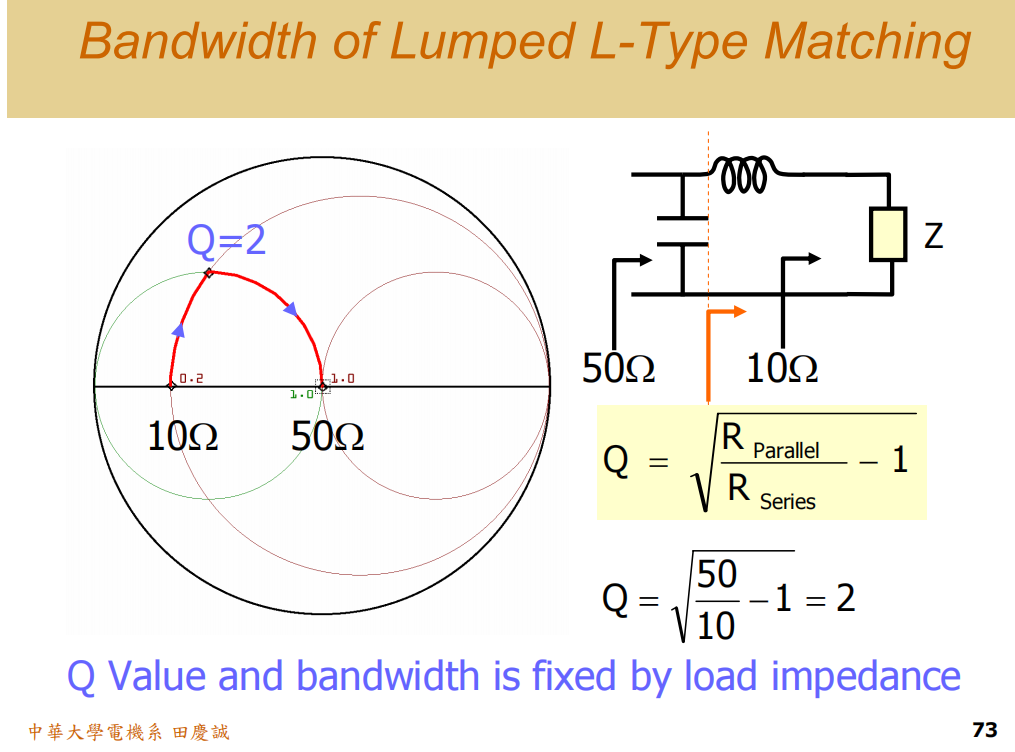
例如，将10欧姆匹配到50欧姆。在圆图上，从10欧姆点通过串联/并联操作到达50欧姆点的路径是唯一确定的 （最多两条路径可选）。这条路径必然经过一个特定的中间点，该点的Q值也就被固定了。
如果这个固定Q值很高，那么用它做出来的匹配网络必然是窄带且高损耗的。你无法用L型网络去"压扁"这条路径。

公式：Q=√RlargeRsmall−1Q = √\frac{R_{large}}{R_{small}} - 1Q=√RsmallRlarge−1

对于10Ω到50Ω的匹配，RlargeR_{large}Rlarge=50，RsmallR_{small}Rsmall=10，代入得 Q = √( (50/10) - 1) = √4 = 2。

重要推论：

带宽固定 ：L型网络的带宽由其Q值决定（BW ≈ f0 / Q），因此带宽也被源/负载阻抗比锁定。当负载阻抗与源阻抗相差越大（R_large/R_small 越大），Q值越高，带宽就越窄。
对元件误差极度敏感（量产噩梦）：高Q值电路（例如Q=7对应1Ω匹配到50Ω）在史密斯圆图上路径很长，对频率极其敏感。频率稍有偏移，或元件值（L, C）有微小误差（市售元件通常有±5%公差），工作点就会严重偏离设计值，导致匹配失效。这样的设计在实验室仿真中可能完美，但在量产时良率会很低，是工程师的大忌。

T型/π型网络

既然L型网络不够灵活，我们就需要更复杂的网络，例如T型或π型网络（使用三个或更多元件）。

但是有一点需要注意，增加元件不一定就能实现宽带，甚至可能更差。比如下面这个例子:

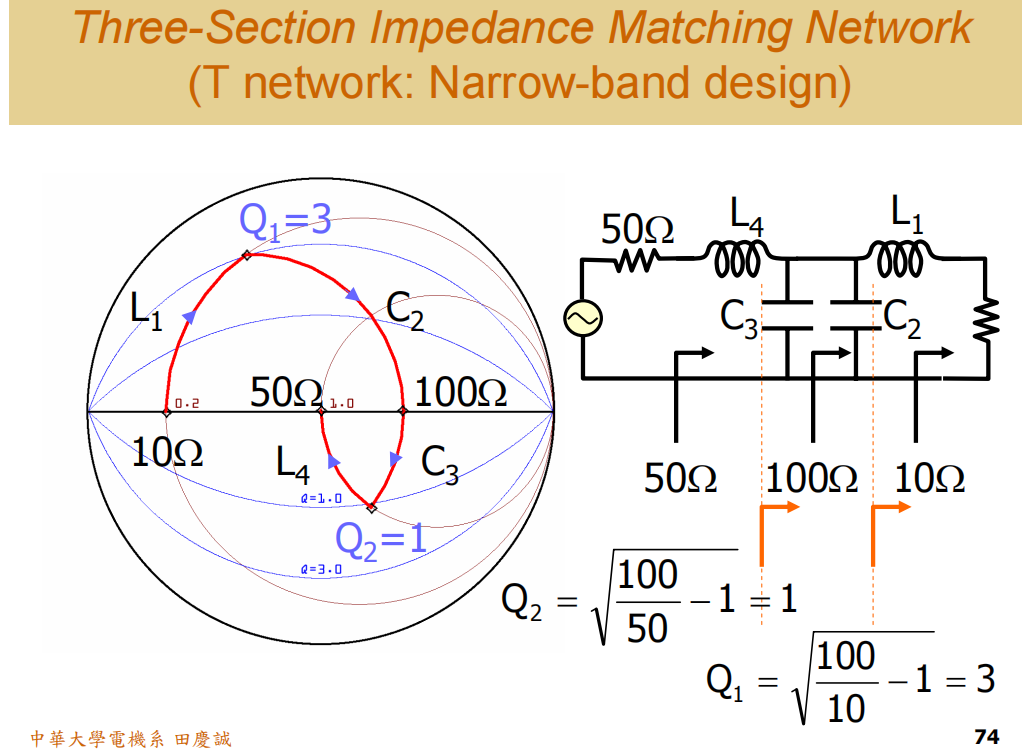
为了将10Ω匹配到50Ω，采用π型网络（串联L1 - 并联两个C - 串联L4）。这个设计可以分解为两个L型级联：10Ω → 某个中间阻抗RmR_mRm → 50Ω。

第一段（10Ω → RmR_mRm）有一个Q1。
第二段（RmR_mRm → 50Ω）有一个Q2。

在这个例子中，我们选择RmR_mRm = 100Ω。那么：

Q1 = √(100/10 - 1) = √9 = 3
Q2 = √(100/50 - 1) = √1 = 1

关键问题出现了，整个级联网络的带宽和稳定性，由两个Q值中较大的那个（Q1=3）决定 。因为这个高Q值环节（对应图中的L1和C）对频率变化最敏感，它会主导整个网络的频率响应，使其比简单的L型网络（Q=2）更窄带、更敏感 。

高Q环节意味着使用了大感抗或大容抗的元件（数值大的L或C）。频率变化Δf时，其电抗变化量ΔX = 2πLΔf 或 ΔB = 2πCΔf 会非常大，导致阻抗点在圆图上剧烈移动，后续环节无法补偿，最终造成严重失配。

下面这个例子，也是如此，虽然增加了元件，但并没有实现宽带

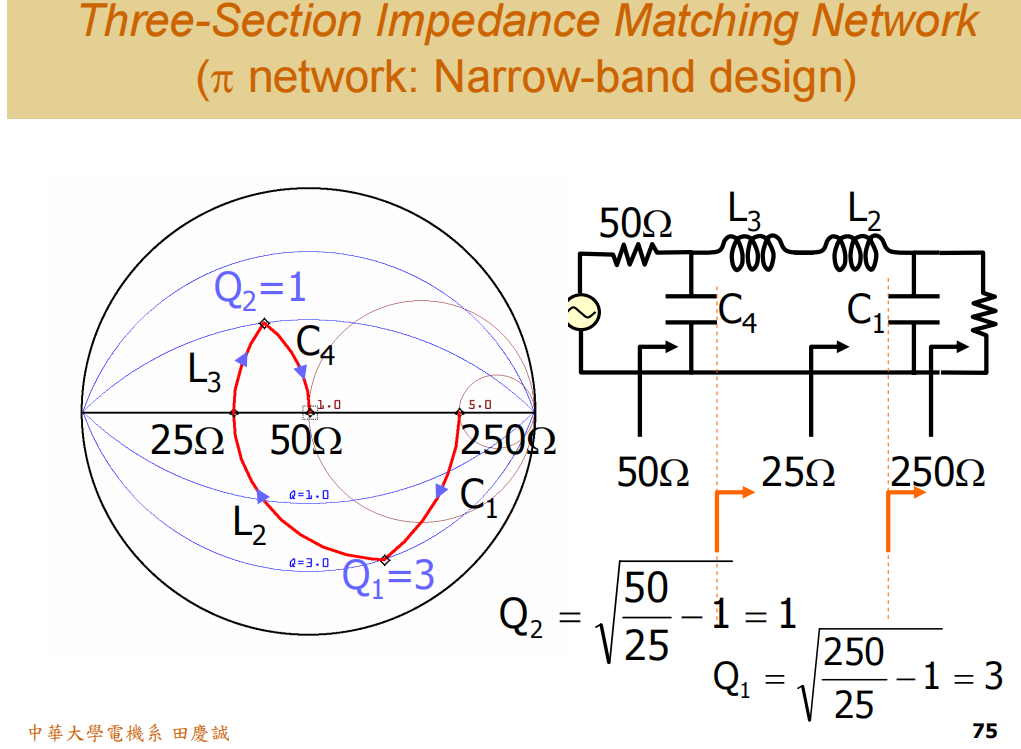
也就是说如果中间阻抗选择不当，反而会引入更高的Q值环节，使性能恶化。

实现宽带匹配

要实现真正的宽带（Broader Bandwidth）匹配，核心思想是：将阻抗变换分解成更多、更小的步进来完成，确保每一步的Q值都尽可能低且相等。

最优设计原则 ：对于N级（N-1个中间阻抗点）匹配，当每一级的Q值都相等 时，能获得理论上该级数下的最平坦带内响应和最大带宽。

以四元件（两级L型级联，三个中间阻抗）将10Ω匹配到50Ω为例：

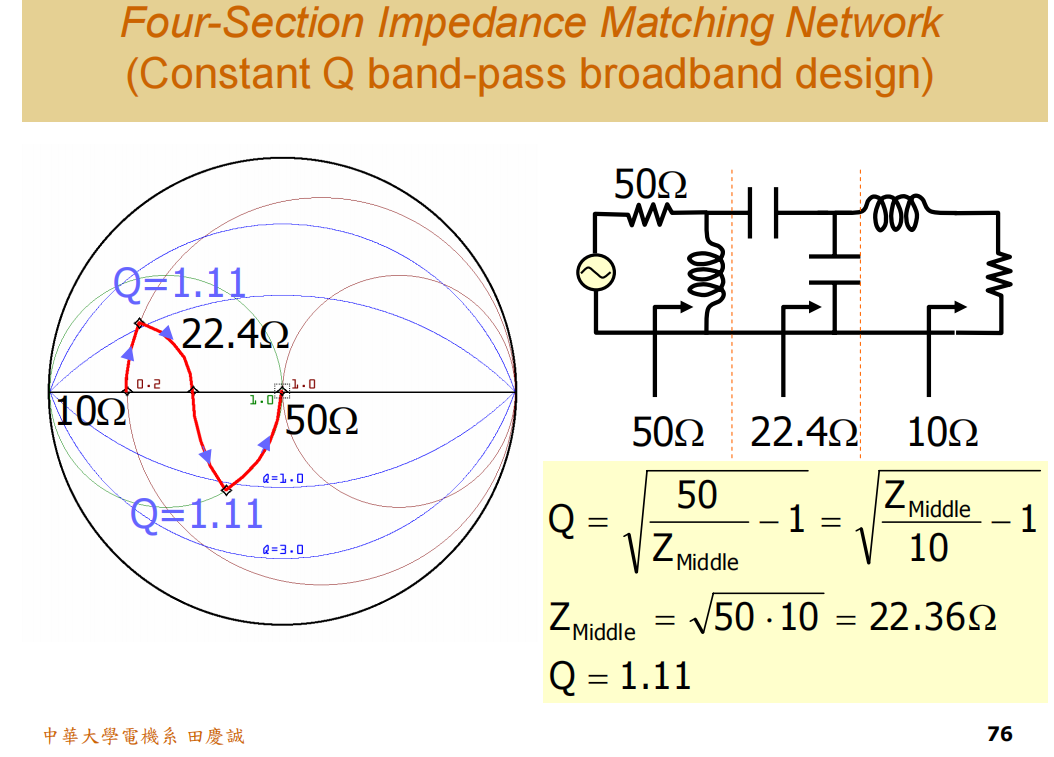
目标是找到中间阻抗RmR_mRm，使得：

第一级 Q1 = √(RmR_mRm/10 - 1)

第二级 Q2 = √(50/RmR_mRm - 1)

令 Q1 = Q2，求解RmR_mRm。

解得：RmR_mRm = √(10 * 50) = √500 ≈ 22.36 Ω

此时，Q1 = Q2 = √(22.36/10 - 1) ≈ √1.236 ≈ 1.11

四级匹配的每级Q值（1.11）低于二级L型匹配的Q值（2）.

这意味着每一小步变换对频率都不敏感，整体带宽得以显著拓宽。

推广到更多元件（更多级） ：

对于从RsR_sRs到RLR_LRL的匹配，如果将其均匀分成n级（即使用2n个元件，形成n级L型级联），那么最优的中间阻抗将构成一个几何级数 ：
R1,R2,...,Rn−1，其中Rk=Rs∗(RL/Rs)k/nR_1, R_2, ..., R_{n-1}，其中 R_k = R_s * (R_L / R_s)^{k/n}R1,R2,...,Rn−1，其中Rk=Rs∗(RL/Rs)k/n

此时，每一级的Q值都相等，且为：Qsingle=(RL/Rs)1/(2n)−1Q_{single} = (R_L / R_s)^{1/(2n)} - 1Qsingle=(RL/Rs)1/(2n)−1 （近似公式，直观理解）
级数n越多，每一级的Q值就越低，总带宽就越宽。

案例(三元件和四元件对比）

我们比较两种匹配方案，工作频率均为1GHz，并考虑电感的实际Q值（这里设定了一个较低的值来模拟芯片上较差的电感），电容视为理想。

方案A（蓝色曲线 - 窄带高损） ：采用三元件T型网络 。其设计路径在史密斯圆图上"绕远路"，中间经过了一个高Q值点（Q=3）。该网络由**两个电感、一个电容(三个元件都为Low-Pass)**构成。
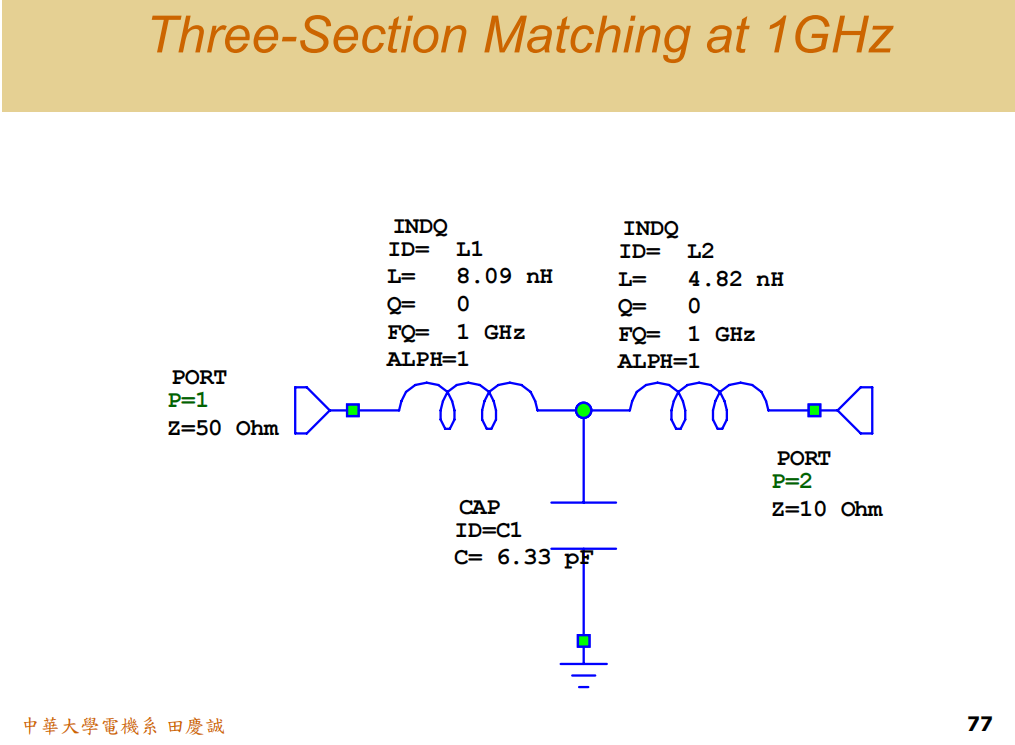
方案B（粉色曲线 - 宽带低损） ：采用四元件网络（两级L型级联） 。其设计路径贴近实轴，每级的Q值都相等且很低（Q=1.11）。该网络也由两个电感、两个电容(左边电感电容为High-Pass元件，右边电感电容为Low-Pass元件 构成。

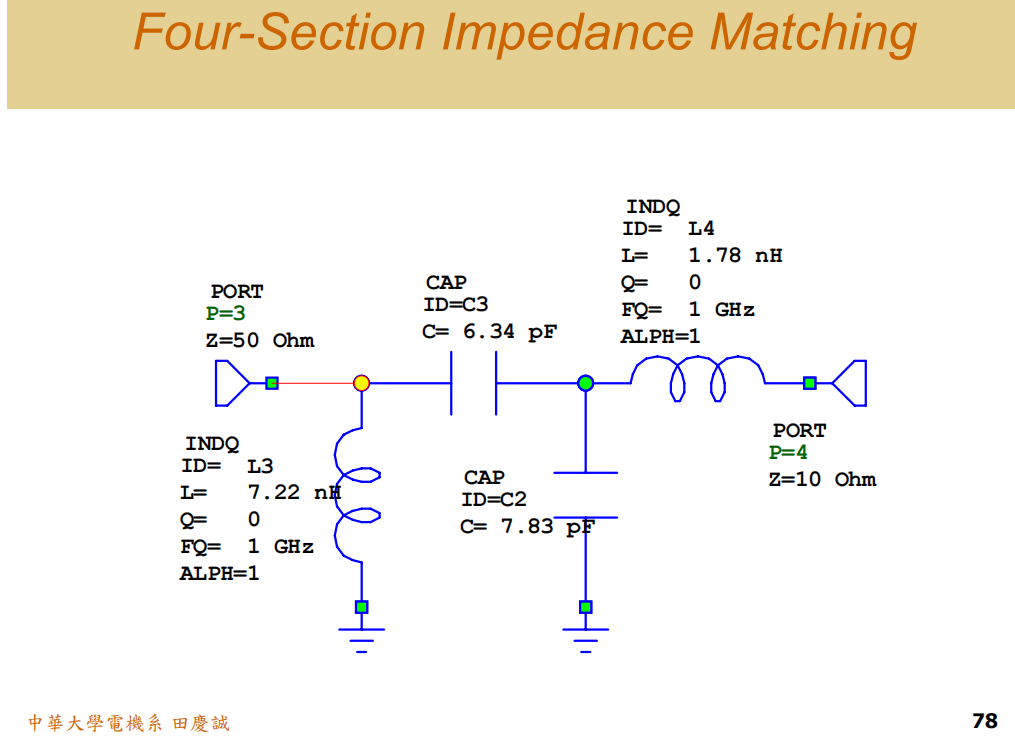
注意：为了公平比较，两种方案都使用了两个电感，避免了因电感数量不同而导致的损耗差异。

仿真结果分析如下

1. 带宽对比

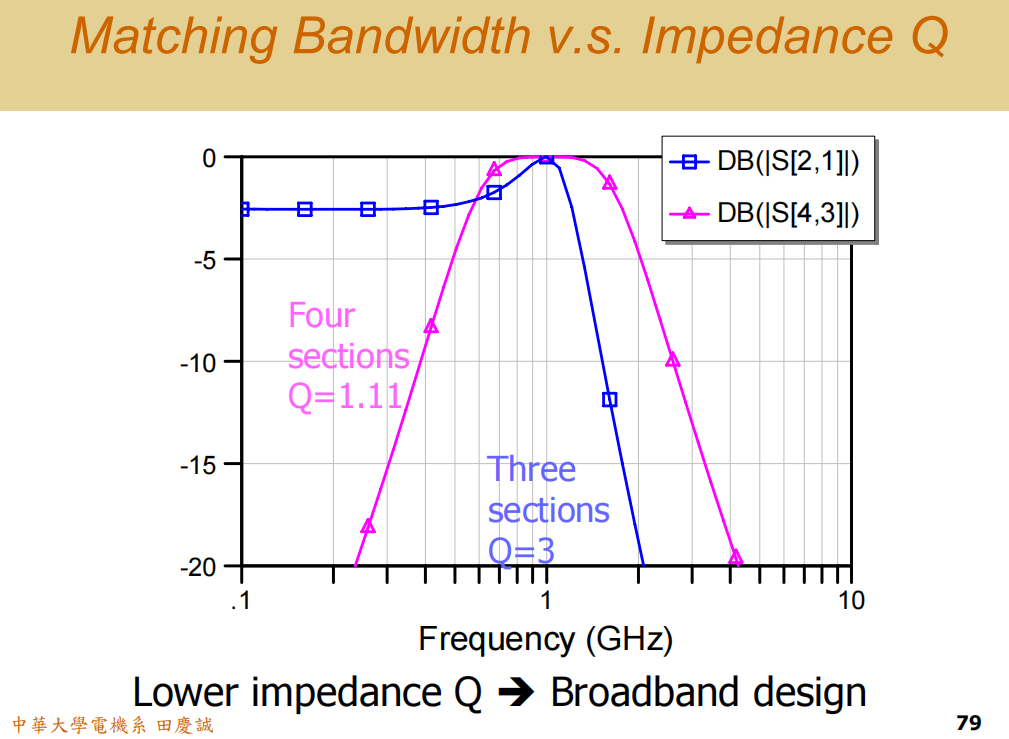
粉色（宽带设计） ：频率响应呈现良好的带通（Bandpass） 形状，对称且平坦。其3dB带宽约为1GHz（从大约0.6GHz到1.6GHz），非常宽。
蓝色（窄带设计） ：频率响应呈现低通（Low-pass） 形状，但通带非常窄且陡峭。在通带边缘衰减得非常快。

结论：低路径Q值（粉色方案）的设计实现了更宽的带宽。

2. 高频衰减斜率验证

在高频区域（远高于中心频率），两种电路的响应都进入直线衰减区，其斜率符合理论：

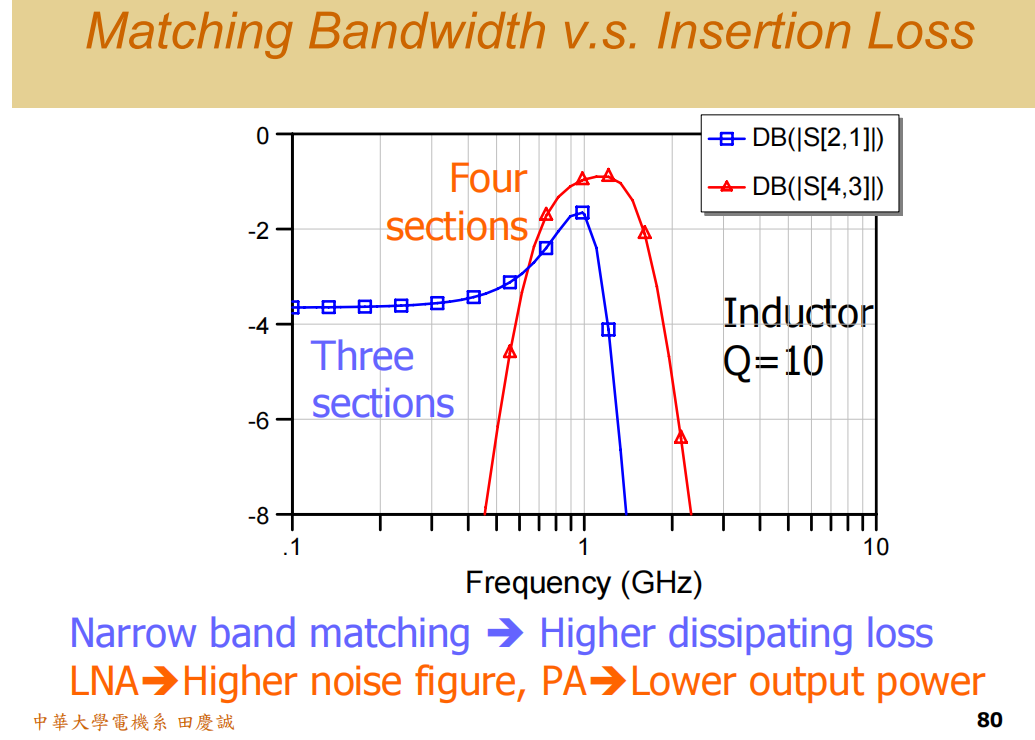
红色方案（两个电感 + 两个电容） ：共有4个电抗元件，每个提供约-20dB/十倍频程的衰减，理论斜率为 -80dB/十倍频程。在2倍频程（Octave）处，理论衰减约 -24dB（4 × -6dB/Oct）。观察图中从2.5GHz到5GHz的衰减，大致符合此理论值。
蓝色方案（两个电感 + 一个电容） ：共有3个电抗元件，理论斜率为 -60dB/十倍频程。在2倍频程处，理论衰减约 -18dB（3 × -6dB/Oct）。观察图中从2GHz到4GHz的衰减，也大致符合。

这验证了我们之前关于多极点网络衰减斜率的理论估算,并且验证了让匹配路径贴近史密斯圆图实轴（低Q路径），不仅能拓宽带宽，更能有效降低匹配网络自身的损耗。

对于低噪声放大器 (LNA) ：输入匹配网络的插入损耗会直接叠加到系统的噪声系数 (Noise Figure) 上。损耗每增加1 dB，噪声系数就增加约1 dB。如果输入匹配损耗高达1.8dB，即使晶体管本身噪声系数很低，整个LNA的噪声性能也会变得很差。

对于功率放大器 (PA) ：输出匹配网络的插入损耗会直接吃掉宝贵的输出功率。损耗1.8 dB意味着近30%的功率被浪费在匹配网络上，这不仅降低了效率，还可能迫使设计者选用成本高得多的大功率晶体管来弥补这部分损失。

因此，在设计LNA和PA时，追求低损耗匹配与追求宽带、良好匹配同等重要。而实现低损耗的秘诀，正是我们反复强调的：设计低Q值的匹配路径（贴近史密斯圆图实轴）。

3. 核心澄清：两种"Q值"的区别

有同学可能会混淆：

负载/路径Q值（我们一直讨论的） ：指在史密斯圆图上，某一特定频率点 的阻抗点（或匹配路径）所对应的Q值（Q = |X|/R）。它衡量的是匹配的难度和潜在带宽。粉色方案的路径Q值（1.11）远低于蓝色方案的最大路径Q值（3）。
电路/滤波器Q值 ：指整个匹配网络作为一个带通或带阻滤波器 时，其频率响应的品质因数。定义为 中心频率 / 3dB带宽 。它衡量的是最终实现电路的频率选择性。

两者关系 ：路径Q值低，意味着更容易实现宽带匹配，因此最终电路的滤波器Q值也倾向于低（即带宽宽）。它们成正比趋势，但数值上并不相等 。

在这个例子中，粉色方案路径Q=1.11，其实现的电路3dB带宽很宽，对应的滤波器Q值也较低；蓝色方案路径最大Q=3，其实现的电路带宽很窄，滤波器Q值较高。

结论

路径Q值决定带宽潜力 ：匹配网络在史密斯圆图上的变换路径，其最大Q值决定了电路最终能达到的带宽上限。Q值越低，潜在带宽越宽。
多级低Q设计是宽带关键 ：通过使用更多元件（如四元件、六元件），并将总阻抗变换分解为多个小步（每步Q值低且相等），可以主动压低路径中的最大Q值，从而实现宽带匹配。方案B（粉色）正是这一原理的成功应用。
元件数不是带宽的保证 ：方案A（蓝色）虽然用了三个元件，但因为中间点选择不当，产生了高Q环节（Q=3），导致其带宽反而比一些两元件设计更窄。"更多元件"必须配合"低Q路径"设计才能拓宽带宽。
在设计匹配网络时，不应只满足于在软件中找到"能匹配"的元件值。应该主动分析或优化匹配路径的Q值，选择那些路径更贴近史密斯圆图实轴的拓扑，这样才能获得性能更优（更宽带宽、可能更低损耗）的设计。

这个实例完美地证明了我们之前的所有理论推导：低Q路径是实现宽带、低损耗匹配的不二法门。

晶体管宽带匹配设计实例演示

上面我们讲的都是无源元件进行匹配，下面我们讲解一个实际晶体管(有源器件)的宽带输出匹配设计，目标是将S11S_{11}S11在1.5 GHz到4.5 GHz的频带内匹配到50欧姆。

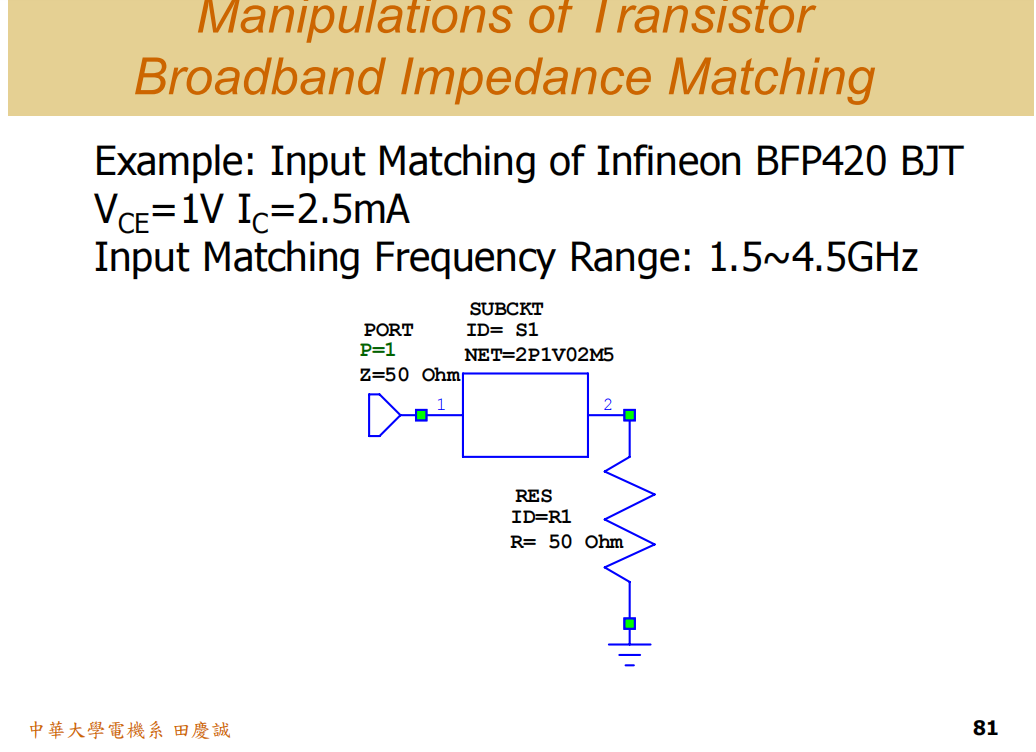
第一步：用传输线进行整体旋转

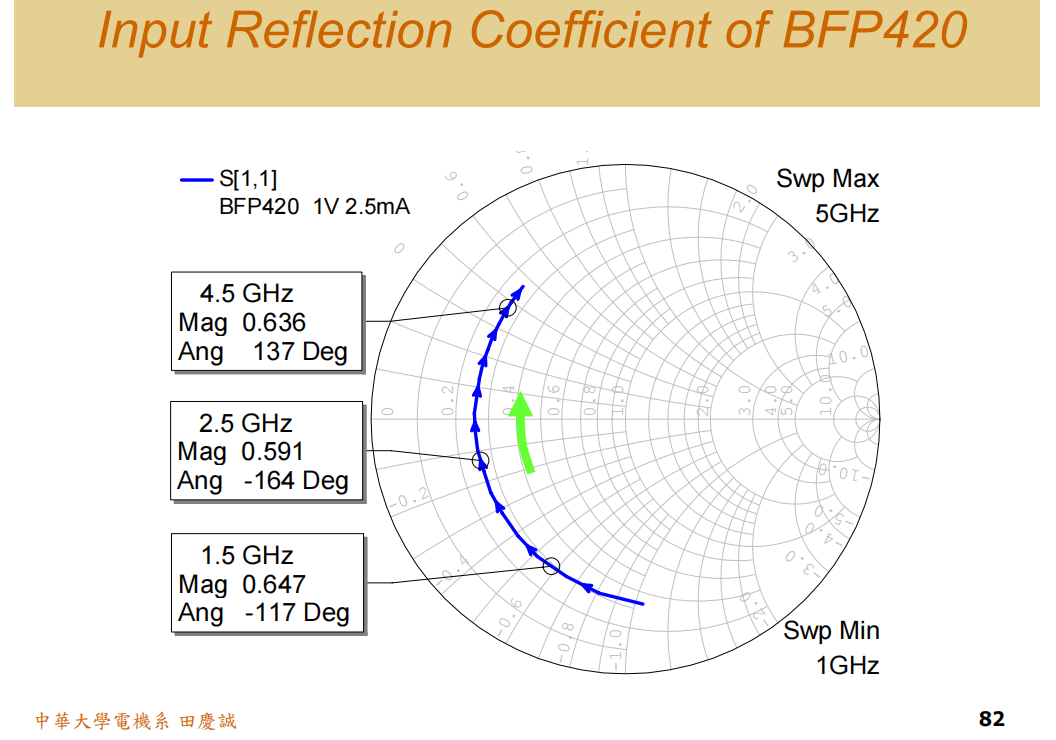
观察初始阻抗轨迹：晶体管的S11轨迹（蓝色曲线）在史密斯圆图上跨度很大，像一个倾斜的环。
中心频率选择 ：带宽为1.5-4.5 GHz，中心频率f0=(1.5+4.5)/2=3GHzf_0 = (1.5+4.5)/2 = 3 GHzf0=(1.5+4.5)/2=3GHz。我们希望将轨迹围绕这个中心频率进行优化。
第一次变换 - 整体旋转 ：我们使用一段 50欧姆传输线 ，长度为8度（在2.5 GHz处，实际物理长度固定，其电长度随频率变化）。这段线的作用是将整个阻抗轨迹顺时针旋转 （向源端移动）。
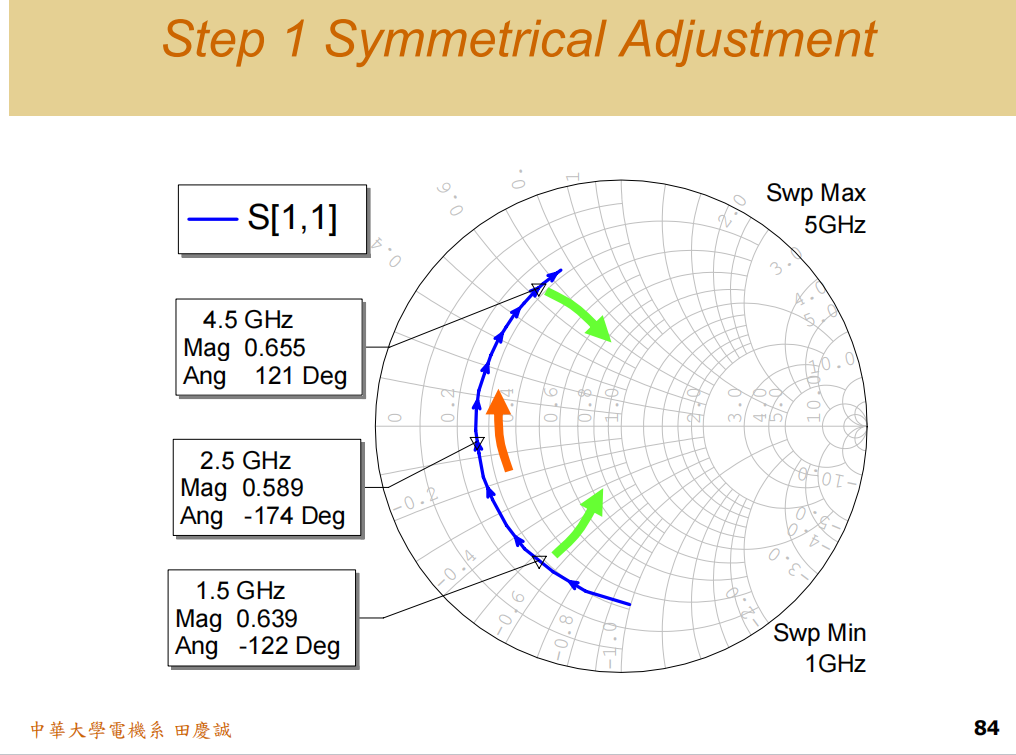
- 效果：旋转后，轨迹整体被"摆正"，高低频两点（1.5G和4.5G）大致关于实轴对称。此时，在中心频率附近，阻抗点看起来像一个 R-L-C串联谐振电路 的轨迹。

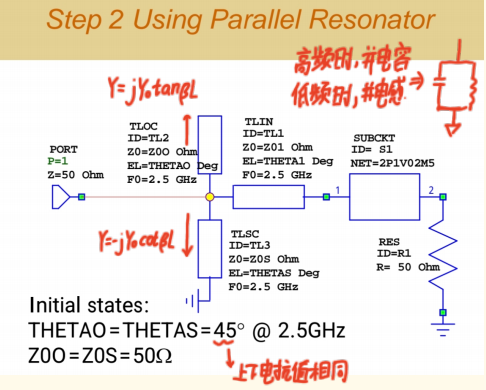
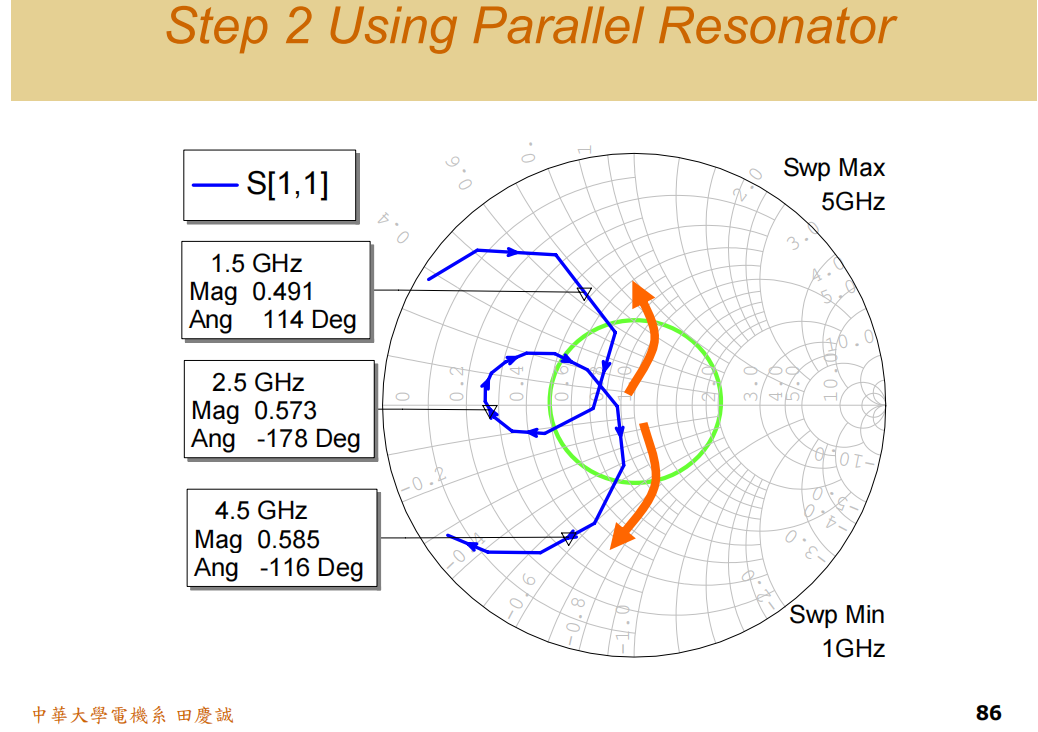
第二步：引入并联谐振器（Resonator）进行压缩

现在需要把"摆正"但依然分散的绿色轨迹，压缩并拉向圆心（50Ω）。

挑战：在宽频带内（1.5G和4.5G），需要同时将轨迹的上下部分都向中心拉拢。一个固定值的并联电容或电感无法做到，因为它们只在一个方向上起作用（电容下拉，电感上拉）。

所以，我们并联一个 LC谐振回路 。这个回路在其谐振频率 f_res 处阻抗为无穷大（开路），因此在fresf_{res}fres处几乎不影响主电路。而在谐振频率两侧：
- 低频时 (f<fresf < f_{res}f<fres) ：LC回路呈感性，等效为一个并联电感，能将阻抗点向上拉。
- 高频时 (f>fresf > f_{res}f>fres) ：LC回路呈容性，等效为一个并联电容，能将阻抗点向下拉。
谐振频率设定 ：我们将谐振回路的fresf_{res}fres设定在中心频率f0=2.5f_0 = 2.5f0=2.5GHz 。这样，在2.5GHz时它不影响电路，而在1.5 GHz和4.5 GHz时，它能分别提供上拉和下拉的力，完美地将绿色轨迹的两端向中心压缩。
实现方式：
- 并联电容 ：在PCB上用 开路支线 (Open Stub) 实现。就是一段终端开路的传输线。在毫米波频段，为了优化性能，其形状可能演变为 径向支线 (Radial Stub)，其原理仍是利用金属平板与地平面间的电容。
- 并联电感 ：用 短路支线 (Short Stub) 实现。是一段终端通过过孔接地的传输线。

关键计算：支线长度

对于特性阻抗为 Z0 的支线，其长度 l 在谐振频率 f_res 下需要满足：jB_cap + jB_ind = 0，即 jY0 tan(βl) + (-jY0 cot(βl)) = 0。这要求 tan(βl) = cot(βl)。满足此条件的电长度 βl = 45° （或 π/4 弧度）。因此，在谐振频率处，开路支线和短路支线的长度都应设计为 λ/8（因为45°是90°的四分之一，而90°对应λ/4）。

加入并联谐振器后，轨迹显示，1.5 GHz和4.5 GHz的点被成功地拉向了中心区域，形成了一个更紧凑的环。但整个环还没有完全进入理想的匹配区域（例如VSWR < 2:1 的圆内）。

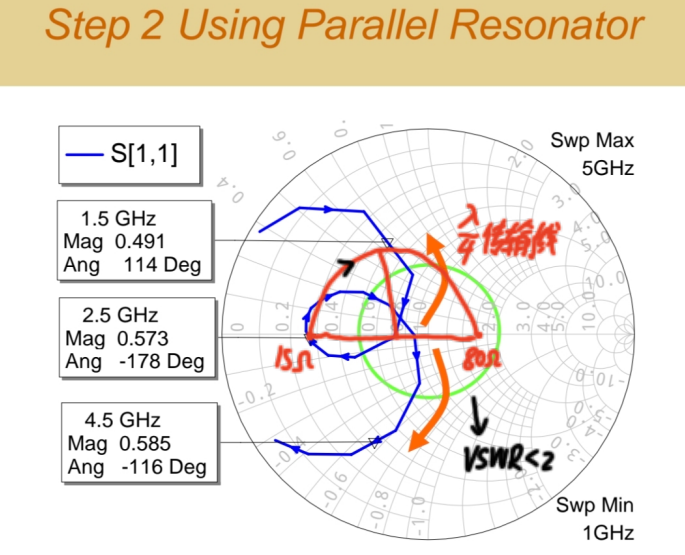
第三步：使用λ/4阻抗变换器进行"平移"

现在需要将这个紧凑的环整体"平移"到圆心附近。

目标：将紫色环，特别是其中心点（约在2.5GHz），移动到50欧姆点附近。
方法：使用 四分之一波长阻抗变换器 。这是一段特性阻抗为 ZtransZ_{trans}Ztrans、长度在中心频率为λ/4λ/4λ/4的传输线。
原理：λ/4 线能将阻抗ZAZ_AZA 变换为ZBZ_BZB，满足ZA∗ZB=Ztrans2Z_A * Z_B = Z_{trans}^2ZA∗ZB=Ztrans2。
设计：
- 我们想将中心点的阻抗（假设为ZcenterZ_{center}Zcenter）变换到50Ω。
- 因此，选择Ztrans=√(50∗Zcenter)Z_{trans} = √(50 * Z_{center})Ztrans=√(50∗Zcenter)。通过观察估算ZcenterZ_{center}Zcenter 大约在15Ω到80Ω之间，取其几何平均数估算Ztrans≈√(80∗15)≈√1200≈34.6ΩZ_{trans} ≈ √(80*15) ≈ √1200 ≈ 34.6ΩZtrans≈√(80∗15)≈√1200≈34.6Ω，因此选择了 35Ω 左右作为变换线阻抗。
- 长度设定为中心频率（2.5GHz）下的90°90°90°（即 λ/4）。

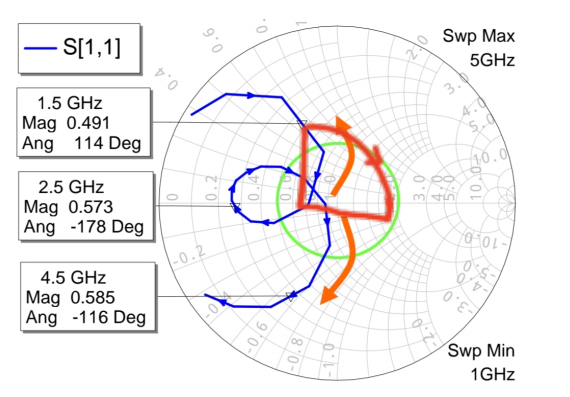
频率响应评估

* 这条35Ω线只在中心频率2.5GHz 处是精确的λ/4λ/4λ/4。

* 在低频1.5 GHz ：电长度变为90°∗(1.5/2.5)=54°90° * (1.5/2.5) = 54°90°∗(1.5/2.5)=54°。因此，环上的1.5 GHz点会沿着一个以35Ω为特征阻抗的等反射系数圆旋转约 2∗54°=108°2*54°=108°2∗54°=108°。通过作图判断，旋转后会进入中心区域。

* 在高频4.5 GHz ：电长度变为90°∗(4.5/2.5)=162°90° * (4.5/2.5) = 162°90°∗(4.5/2.5)=162°。环上的4.5 GHz点会旋转约324°324°324°，几乎绕圆一圈，也有机会进入中心区域。

加入这段35Ω的 λ/4 线后，最终阻抗轨迹的整个环被成功地"平移"并压缩到了50欧姆点附近 ，在1.5 GHz至4.5 GHz的宽频带内，基本都落在了VSWR < 2:1 的绿色圆内，实现了出色的宽带匹配。

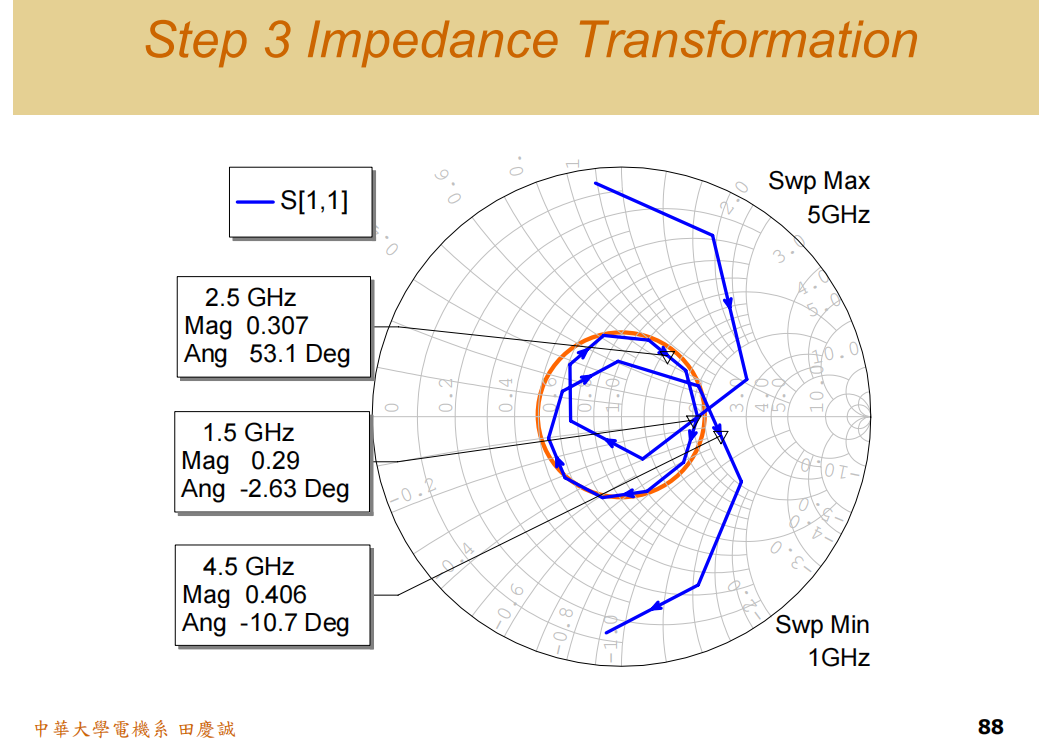
设计总结

旋转 (Rotate)：用传输线校正轨迹的相位/角度，使其对称。
压缩 (Compress)：用并联谐振器利用其频率变抗特性，将轨迹两端向中心压缩。
平移 (Translate) ：用 λ/4 阻抗变换器将整个轨迹平移到目标阻抗点。

第四步：利用软件进行自动优化 (Optimization)

在完成初步设计后，我们得到了一个基本满足要求的匹配网络。但要达到最佳性能，需要借助仿真软件的优化工具。

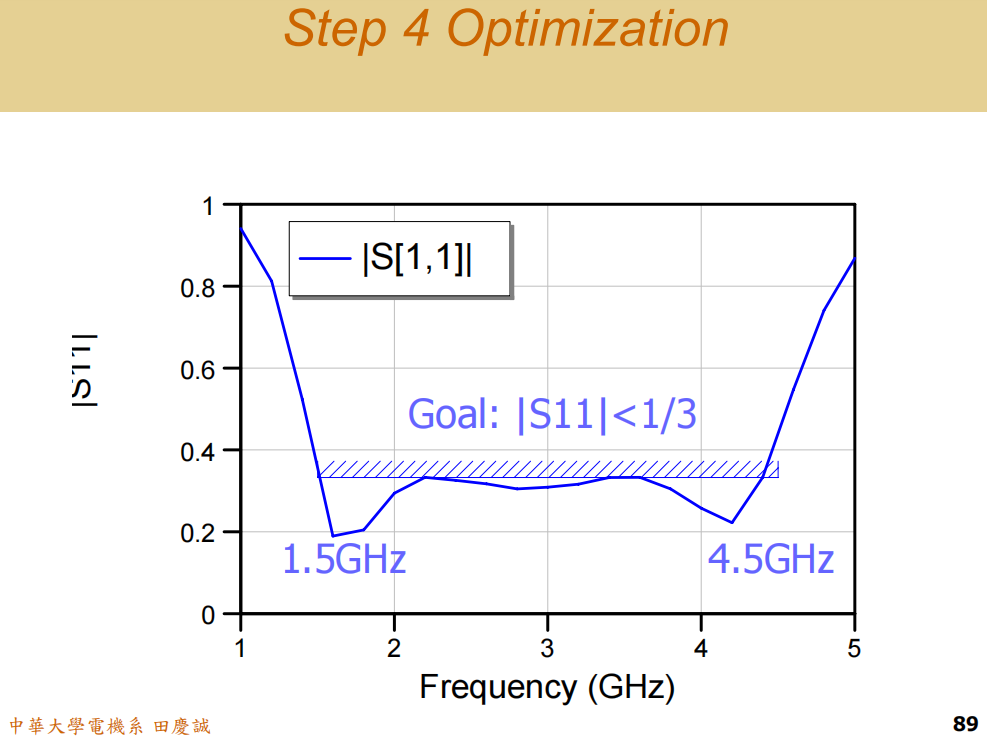
优化目标 (Goal) 的设定：
- 建议使用 S11的绝对值（模值） 作为优化目标，而不是它的dB值。例如，设定目标为 |S11| < 1/3。
- 为什么是1/3？ 这对应于电压驻波比 VSWR ≈ 2:1，是一个在宽带匹配中常见且合理的指标。换算成dB值约为 -9.5 dB。
- 为什么用绝对值？ 有些软件（如您提到的特定版本）的优化器在处理dB值（对数尺度）时可能不够稳定或高效。绝对值是线性尺度，优化算法处理起来更直接、更鲁棒。
优化中的权衡哲学：
- 在优化时，我们追求的不是让频带内某几个点无限趋近于完美匹配（S11=0S_{11} = 0S11=0），而是让整个目标频带（1.5-4.5 GHz）内的S11都均匀地低于某个阈值（如1/3）。
- 如果您强行把中间某些点的S11压得非常低，根据波德-法诺准则，这必然会导致频带边缘的S11恶化，或者整体带宽缩窄。
- 最优的宽带响应，往往是频带内反射系数大小近乎"平坦"的响应，而不是一个有很多深谷的崎岖曲线。优化器的任务就是找到元件值的组合，实现这种最均衡、带宽最宽的效果。

从优化结果中学习与反向指导设计

优化不仅仅是一个"黑箱"过程。分析优化后的结果，能给我们带来宝贵的设计洞察：

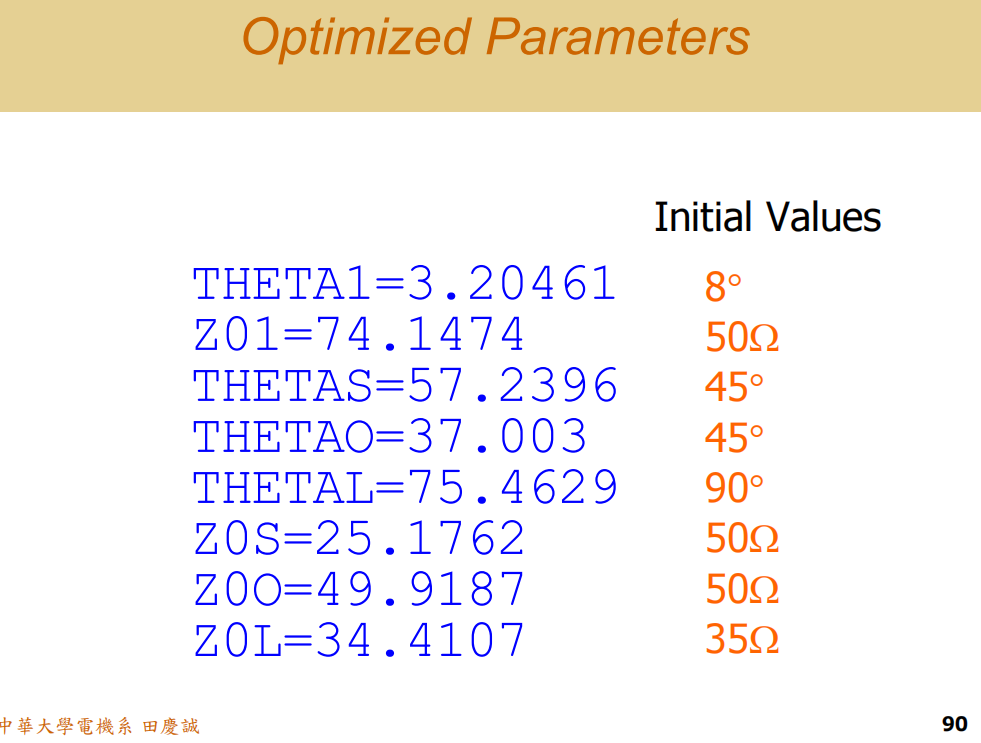
验证设计直觉 ：最初猜测，用于旋转的那段传输线，其特性阻抗大于50欧姆可能会得到更优的旋转路径（半径更大的圆）。优化器运行后，确实将这段线的阻抗推向了更高的值（例如75欧姆附近）。
发现可调整参数：优化器可能会对您最初设定的固定值进行微调，例如：
- 并联谐振器的谐振频率（通过微调L、C值）可能从精确的3 GHz稍有偏移。
- 开路/短路支线的电长度可能从45°调整到更优值。
- λ/4变换线的长度可能不再是精确的90°，而是75°或其它角度。
- 各传输线的特性阻抗值得到最终确认。
- 这些微调都是软件在综合平衡整个频带响应后得到的结果。

两级放大器级联的匹配策略

谈完无源器件，晶体管等有源器件匹配后，我们再来谈最后一部分的内容，放大器的匹配。

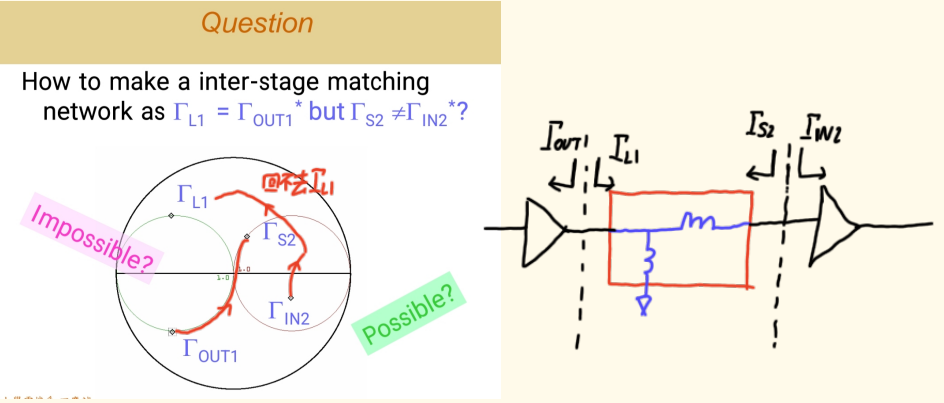
首先，必须牢记匹配的方向性 。我们设计匹配网络时，始终是从源端向负载方向看 进行设计（在史密斯圆图上表现为"向负载端移动"）。反向设计会导致严重错误。

对于两级放大器（如两级LNA或两级PA），中间级（Interstage）的匹配有两种主要思路：

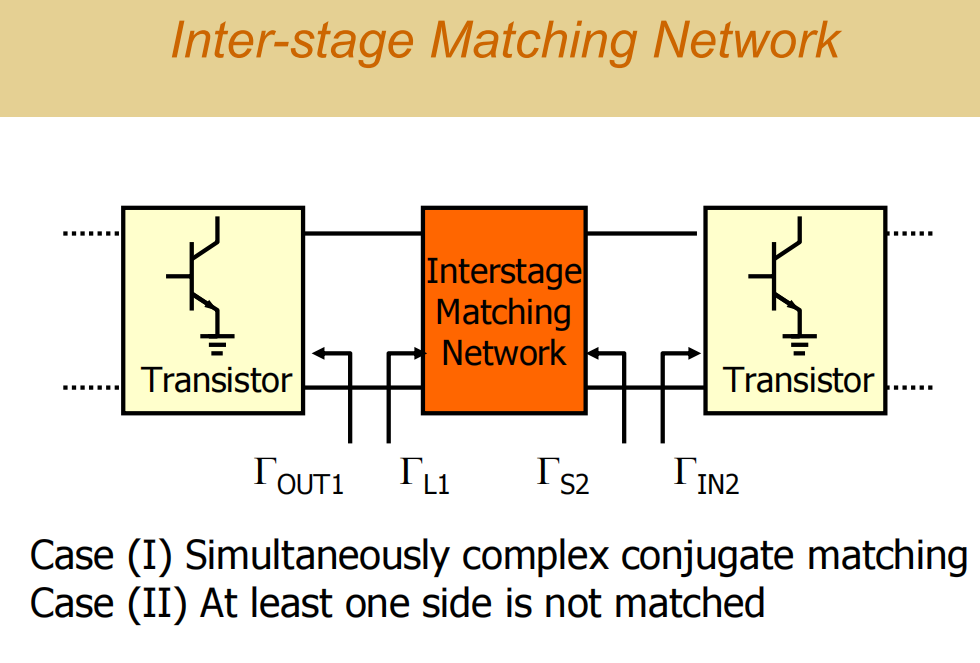
Case 1: 双向同时共轭匹配（Simultaneous Complex Conjugate Matching）

这是最理想、最简单的中间匹配目标 。

目标：使第一级晶体管的输出阻抗（Γout1Γ_{out1}Γout1） 与第二级晶体管的输入阻抗（Γin2Γ_{in2}Γin2）的共轭（Γin2Γ_{in2}Γin2） 相匹配。同时，从第一级看过去的负载反射系数（ΓL1Γ_{L1}ΓL1）也要是Γout1Γ_{out1}Γout1的共轭。
条件：要实现这种完美的双向无反射传输，中间匹配网络必须是严格无耗的（只有纯电感和电容，没有电阻）。任何损耗（包括电感、电容的寄生电阻）都会破坏完美的共轭关系。
现实：现实中不存在绝对无耗的元件，因此只能做到"非常接近"。但这种设计思路清晰，是大多数通用增益放大级联的首选方法，仿真和实际结果通常能很好吻合。

总结：鼓励大家在设计普通增益级联时，优先采用这种"双向共轭匹配"的思路。

Case 2: 单边匹配（One-Side Matching）

在很多高性能设计中，放大器两级的目标并非都是最大增益，这导致中间匹配无法（也不应）实现双向共轭。

A. 两级低噪声放大器（LNA）的情况：

第一级LNA ：首要目标是最低噪声系数（Noise Figure） 。这要求其源端反射系数为 ΓoptΓ_{opt}Γopt （最优噪声反射系数），而不是其输入阻抗的共轭（Γin1∗Γ_{in1}^*Γin1∗）。即：ΓSΓ_SΓS = ΓoptΓ_{opt}Γopt ≠ Γin1∗Γ_{in1}^*Γin1∗。
第二级LNA ：如果它也追求低噪声，同样需要 ΓS2Γ_{S2}ΓS2 = Γopt2Γ_{opt2}Γopt2。
中间匹配困境 ：此时，中间匹配网络需要将一个非共轭匹配点（Γopt1Γ_{opt1}Γopt1对应的输出阻抗）匹配到另一个非共轭匹配点（Γopt2Γ_{opt2}Γopt2）。这是一个双重非共轭匹配问题，非常复杂。
更实用的策略：
1. 第一级 ：精心设计，实现 ΓS1Γ_{S1}ΓS1 = Γopt1Γ_{opt1}Γopt1 以获得最佳噪声。同时尽量优化其增益。
2. 第二级 ：不必强求其噪声最优 。将第二级视为一个提供增益的驱动级 。此时，中间匹配可以采用 Case 1 的双向共轭匹配 ，即匹配第一级的输出（Γout1Γ_{out1}Γout1）到第二级的输入共轭（Γin2∗Γ_{in2}^*Γin2∗）。这样做设计简单，系统总噪声主要由第一级决定，整体性能更可控。
3. 典型架构 ：LNA (噪声优化) -> 匹配网络（双向共轭） -> 驱动放大器（增益优化）。

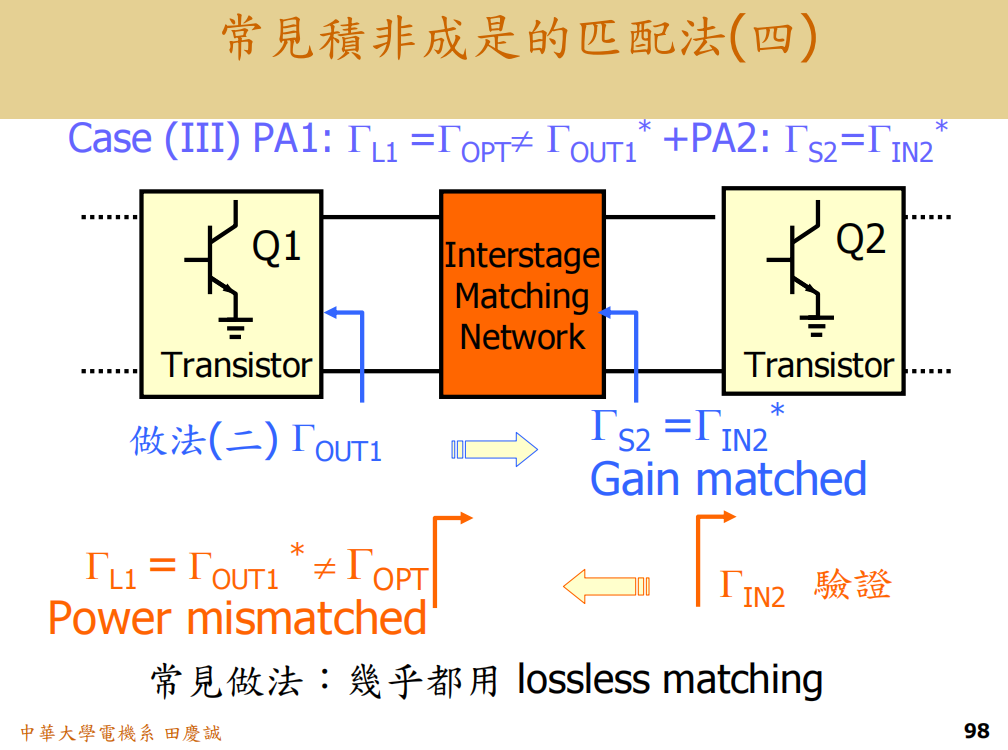
B. 功率放大器（PA）的情况：

核心目标 ：最大输出功率 和效率，而非最大增益。
负载牵引（Load Pull） ：PA晶体管有一个能产生最大输出功率的最佳负载阻抗（ΓLoptΓ_{Lopt}ΓLopt） ，这通常不等于 其输出阻抗的共轭（Γout∗Γ_{out}^*Γout∗）。即：ΓL=ΓLopt≠ΓoutΓ_L = Γ_{Lopt} ≠ Γ_{out}ΓL=ΓLopt=Γout。
输入匹配 ：输入匹配的目标通常是实现最大功率传输（即共轭匹配 ΓS=Γin∗Γ_S = Γ_{in}^*ΓS=Γin∗），以驱动晶体管进入充分工作状态。
中间匹配困境（对于两级PA） ：第一级PA（驱动级）的输出需要匹配到第二级PA（末级）的输入共轭（Γin2∗Γ_{in2}^*Γin2∗） ，但第二级PA自身的输出又需要匹配到其最佳功率负载（ΓLopt2Γ_{Lopt2}ΓLopt2）。这又是一个混合目标。
设计重点 ：对于PA，输出匹配（匹配到ΓLoptΓ_{Lopt}ΓLopt）的优先级远高于级间匹配。级间匹配可以适当放松，甚至允许一定失配，以确保末级的输出功率和效率达标。牺牲一些级间增益来换取整体效率是常见的权衡。

关于课本与现实的差异警告

很多课本重点讲解 Case 2（单边或特殊匹配） 的理论，这本身没错。但问题在于：

仿真与实际的差距：在软件中，我们可以精确设定 Γ_opt 等目标并进行优化。但在实际电路中，元件损耗、寄生效应、PCB误差等会使得最终实现的阻抗偏离设计值。对于本就"紧绷"的非共轭匹配设计，这种偏离可能导致性能（如增益、噪声、功率）严重劣化，与课本或仿真结果相差甚远。
设计的复杂性 ：Case 2 的设计本身就更复杂，对误差更敏感。而 Case 1（双向共轭） 的设计更鲁棒，对元件非理想性的容忍度更高。

除非有非常明确且必须的指标要求（如极限低噪声或极限输出功率），否则对于级联放大器的中间匹配，应优先考虑采用双向共轭匹配（Case 1）这一更稳健、更易实现的设计思路。

对于LNA，将噪声优化重任放在第一级；

对于PA，将功率优化重任放在输出级。这样能有效分解设计难度，提高整体设计的成功率和可重复性。

一个纯粹无耗（只有L、C）的双端口网络，无法实现一侧共轭匹配而另一侧失配。

原因：对于无耗互易网络，其S参数满足幺正性（[S]T[S]∗=[I][S]^T [S]^* = [I][S]T[S]∗=[I]）。如果一端完全匹配（S11=0S_{11} = 0S11=0），根据幺正性可以推导出另一端也必然完全匹配（S22=0S_{22} = 0S22=0），或者网络具有全通或全阻等特殊但无用的性质。换句话说，无耗网络的输入输出匹配状态是强关联的，你无法单独控制一端而让另一端任意失配。

物理意义 ：在无耗网络中，没有被反射的能量不会被电阻吸收，只能在网络内部或端口间来回反射。如果一端完全匹配（无反射），那么从另一端入射的能量必须全部被传输或吸收
但在无耗条件下，吸收不可能，所以只能全部传输，这就要求另一端也必须是匹配的，否则会有能量反射回去，破坏第一端的无反射状态。
因此，要实现"一端匹配，一端特定失配"，网络中必须包含有耗元件（电阻）**来吸收掉那部分因失配而产生的反射能量。

错误案例剖析：两级功率放大器的级间匹配

有工程师认为，对于两级功率放大器（PA）：

第一级PA 输出：需要看到其最佳功率负载（ΓLopt1Γ_{Lopt1}ΓLopt1）。
第二级PA 输入：需要其输入共轭匹配Γin2∗Γ_{in2}^*Γin2∗以获取最大驱动。
他的解决方案 ：分别设计两个独立的匹配电路：
- 电路A：将ΓLopt1Γ_{Lopt1}ΓLopt1匹配到 50Ω。
- 电路B：将 Γin2∗Γ_{in2}^*Γin2∗匹配到 50Ω。
- 然后将这两个50Ω端口直接背靠背连接，认为这就完成了级间匹配。

这个方案的谬误在于：

目标混淆 ：电路A的输出端确实是50Ω，但那是从电路A的源端（接PA1P_{A1}PA1输出）看进去的50Ω。当它连接到电路B的输入端时，对于电路B来说，其源阻抗确实是50Ω，这没错。
但PA1P_{A1}PA1看到的是什么？ PA1P_{A1}PA1看到的负载是整个级联网络（电路A+电路B+PA2P_{A2}PA2）的输入阻抗 。这个阻抗绝对不是电路A单独设计时假定的50Ω负载！因为电路B的接入改变了整个网络的阻抗。
结果：PA1P_{A1}PA1实际看到的负载严重偏离了其最佳功率负载 ΓLopt1Γ_{Lopt1}ΓLopt1，导致其输出功率和效率远低于预期。两个"局部最优"的简单拼接，无法实现"全局最优"。

这个想法失败的数学根源，就是我们之前提到的：一个无耗互易网络，不可能实现一端是任意指定的非共轭阻抗，另一端是共轭匹配。 如果一端匹配了，另一端必然也是匹配的（对于该端的共轭点）。如果一端是特定的ΓLopt1Γ_{Lopt1}ΓLopt1（非共轭点），那么另一端也必然是一个对应的特定点，而不会是任意的Γin2∗Γ_{in2}^*Γin2∗。

常见错误设计方法

教科书和业界中流传的几种看似合理、实则存在固有缺陷的两级放大器设计流程。这些流程都试图用无耗网络 去解决一个本质上需要损耗的问题，因此必然"顾此失彼"。

场景一：两级低噪声放大器（LNA）

目标：第一级要噪声匹配（ΓS1Γ_{S1}ΓS1 = Γopt1Γ_{opt1}Γopt1），第二级也要噪声匹配（ΓS2=Γopt2Γ_{S2} = Γ_{opt2}ΓS2=Γopt2）。
错误方法A（从第二级输入开始设计）：
1. 从第二级输入共轭点（Γin2∗Γ_{in2}^*Γin2∗）出发，用无耗网络匹配到第一级的最佳噪声点（Γopt1Γ_{opt1}Γopt1）。
2. 问题：这样设计出来的网络，其 S11S_{11}S11 必然是Γin2∗Γ_{in2}^*Γin2∗ （共轭匹配），但这不等于 Γopt2Γ_{opt2}Γopt2！因此，第二级的噪声匹配（ΓS2Γ_{S2}ΓS2 = Γopt2Γ_{opt2}Γopt2）被破坏了 。你保住了第一级的噪声和增益，但牺牲了第二级的噪声。
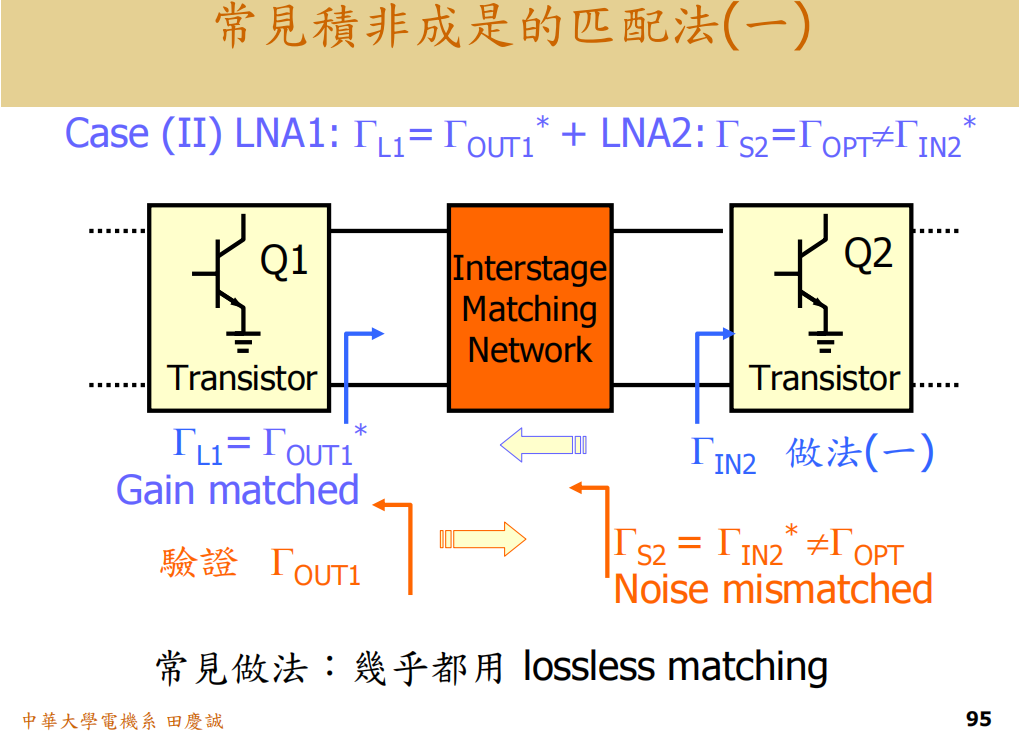
错误方法B（从第一级输出开始设计）：
1. 从第一级最佳噪声点对应的输出阻抗出发，用无耗网络匹配到第二级的最佳噪声点（Γopt2Γ_{opt2}Γopt2）。
2. 问题：这样设计出来的网络，其 S22S_{22}S22 是 Γopt2Γ_{opt2}Γopt2 ，但这不等于 Γin2∗Γ_{in2}^*Γin2∗。因此，第二级的输入不再是共轭匹配 ，其增益会下降。你保住了第二级的噪声，但牺牲了第二级的增益（进而可能影响整体噪声系数，因为第二级增益下降会使第一级噪声贡献更大）。

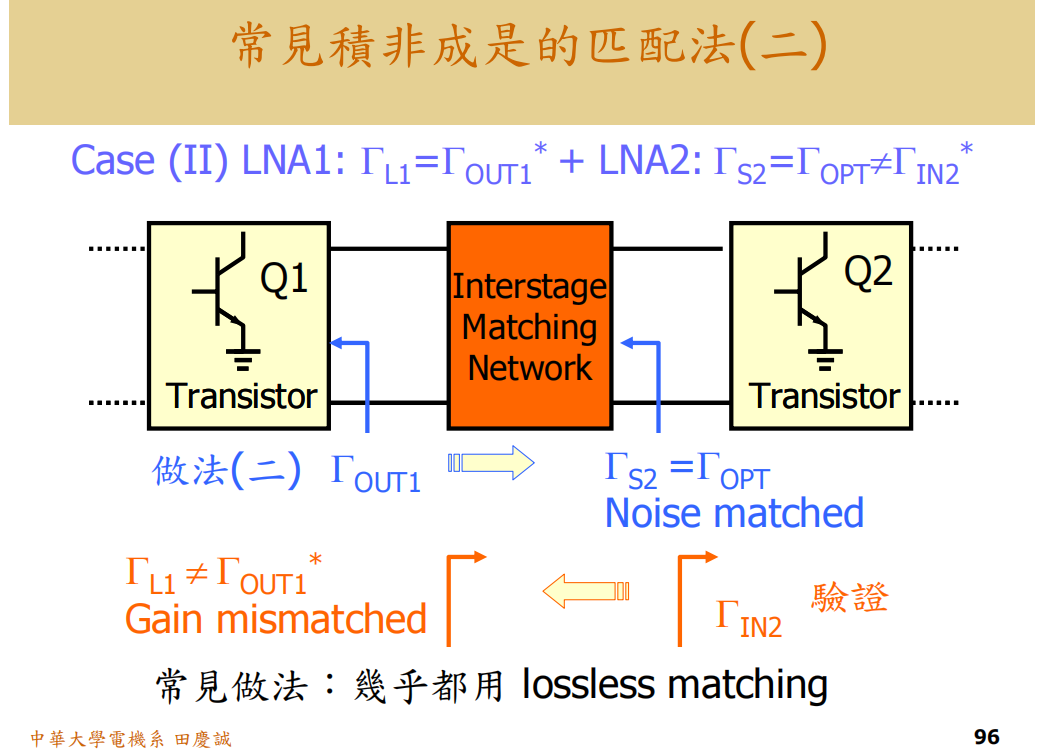
场景二：两级功率放大器（PA）

目标：第一级要看到最佳功率负载（ΓL1Γ_{L1}ΓL1 = ΓLopt1Γ_{Lopt1}ΓLopt1），第二级输入要共轭匹配（ΓS2Γ_{S2}ΓS2 = Γin2∗Γ_{in2}^*Γin2∗）以获得驱动，第二级输出也要看到最佳功率负载（ΓL2Γ_{L2}ΓL2 = ΓLopt2Γ_{Lopt2}ΓLopt2）。
错误方法A（从第二级输入开始设计）：
1. 从第二级输入共轭点（Γin2∗Γ_{in2}^*Γin2∗）出发，用无耗网络匹配到第一级的最佳功率负载点（ΓLopt1Γ_{Lopt1}ΓLopt1）。
2. 问题：同样，网络S11S_{11}S11 = Γin2∗Γ_{in2}^*Γin2∗，但第二级输出端看到的负载不再是其最佳功率负载ΓLopt2Γ_{Lopt2}ΓLopt2（因为网络改变了负载）。你确保了第一级的功率输出和第二级的输入匹配（增益），但牺牲了第二级的输出功率和效率 。
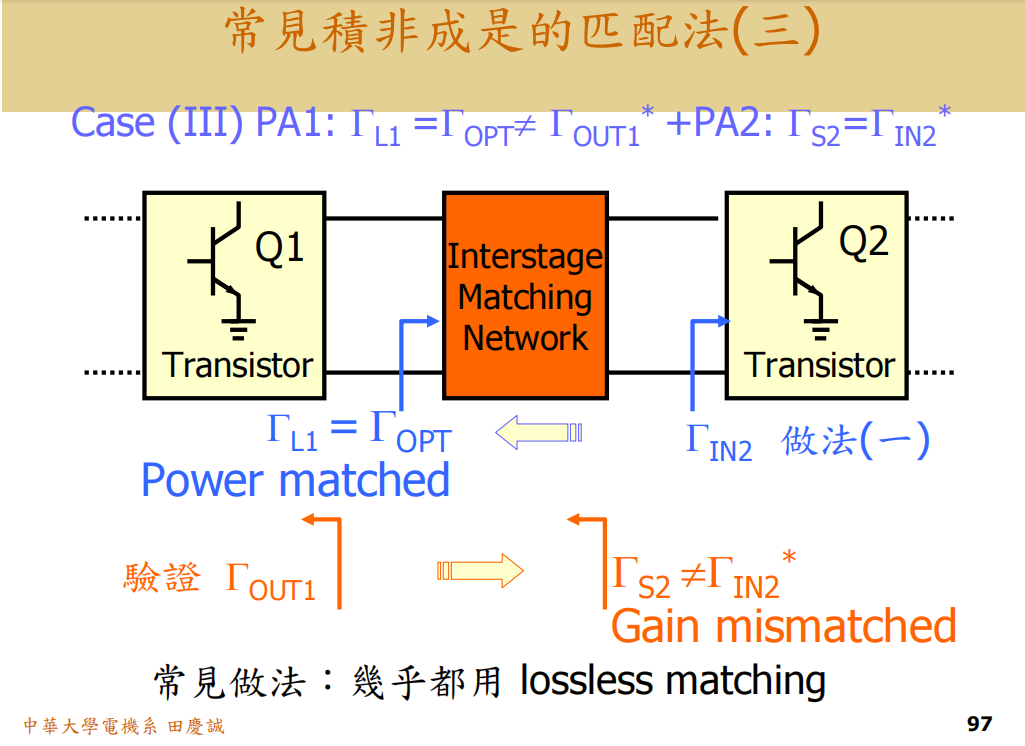
错误方法B（从第一级输出开始设计）：
1. 从第一级最佳功率负载点（ΓLopt1Γ_{Lopt1}ΓLopt1）出发，用无耗网络匹配到第二级输入共轭点（Γin2∗Γ_{in2}^*Γin2∗）。
2. 问题：网络S22S_{22}S22 = Γin2∗Γ_{in2}^*Γin2∗，但第二级输入端看到的源阻抗不再是其输入共轭（因为设计起点是ΓLopt1Γ_{Lopt1}ΓLopt1，而非Γin2∗Γ_{in2}^*Γin2∗的完整网络）。你确保了第一级的功率输出，但牺牲了第二级的输入匹配（增益） ，同样影响驱动和最终输出。

给工程师的宝贵建议

面对这种复杂的两级放大器设计：

优先采用稳健策略：尽量避免两级都追求极端性能（如两级极致低噪声或两级极致高效率）。更稳健的做法是：
- 对于LNA ：第一级专注优化噪声 （ΓS1=Γopt1Γ_{S1} = Γ_{opt1}ΓS1=Γopt1），第二级作为增益级，采用双向共轭匹配（保证增益）。系统噪声主要由第一级决定。
- 对于PA ：末级（输出级）专注优化功率和效率 （匹配到ΓLoptΓ_{Lopt}ΓLopt），前级（驱动级）作为增益级，采用双向共轭匹配（保证足够的驱动增益）。系统效率主要由末级决定。
接受权衡，迭代优化 ：如果必须两级都追求高性能（如级联PA），必须清醒认识到增益、噪声、功率之间的固有矛盾。这时的设计是一个复杂的多目标优化过程，可能需要：
- 在级间网络中引入可控的损耗（电阻）来调和矛盾。
- 使用仿真软件进行全局联合优化，而不是分步独立设计。
- 接受某些指标的适度折衷。
尝试用纯LC网络实现"一端匹配，一端不匹配"------是极好的学习方式。通过亲自推导或仿真，将会深刻理解无耗网络的局限性，从而在未来设计中避免陷入理论陷阱。