1.买卖股票的最佳时机
因为买入要在卖之前，所以需要一个minPrice不断更新到第i天的最低价，不断的用当天的price减去一直维护的minPrice，最终即是答案
两个变量：minPrice和pricei
class Solution:
def maxProfit(self, prices: List[int]) -> int:
ans = 0
minPrice = prices[0]
for p in prices:
ans = max(ans,p-minPrice)
minPrice = min(minPrice,p)
return ans2.最大子数组和
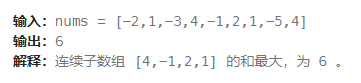具有最大和的连续子数组
首先想到回溯法
回溯公式：dfs(i) = max(dfs(i-1),0)+numsi
dfs定义，以i结尾的最大子数组和
为什么是max和0比，因为如果dfs（i-1）是负数，那最大子数组不就是dfsi自己吗，为什么要带上dfs（i-1）
边界条件：if i==0: return nums0
特殊的地方是ans首先取值要为-inf
时间复杂度：n 空间复杂:n
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
# ans = -inf
# @cache
# def dfs(i):
# if i==0:
# return nums[0]
# else:
# return max(dfs(i-1),0)+nums[i]
# for i in range(len(nums)):
# ans = max(ans,dfs(i))
# return ans一维数组
这个题不需要f的长度为n+1，因为只需要和前一个比较，不像爬楼梯那些，需要和前一个，前两个比较，所以引入了虚拟起点，这样dp[2] 需要单独写 dp[2]=2，无法复用 dp[i] = dp[i-1]+dp[i-2]；
本题只需要n，而且f0就是nums0
时间复杂度n，空间复杂度n
f = [0]*len(nums)
f[0] = nums[0]
for i in range(1,len(nums)):
f[i]=max(f[i-1],0)+nums[i]
return max(f)空间优化
只需要一个f记录之前的前缀和
时间复杂度n，空间复杂度1
ans = -inf
f = 0
for x in nums:
f = max(f,0)+x
ans = max(ans,f)
return ans前缀和法
想象一下，现在手里有最小前缀和，和一直枚举的当前前缀和，用当前前缀和不断的减去最小前缀和，刷新出的最大值，就是解
为什么
因为最小前缀和，说明加上这些会导致最终的值变小啊，所以当前的前缀和减掉这部分前缀，剩余的就是大的
因此我们需要一个不断刷新的minPrice，和股票一样，先计算ans，再去更新minPrice
前缀和是和遍历前缀和同步进行的，和560题一样
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
minPre = sumPre = 0
ans = -inf
for p in nums:
sumPre += p
ans = max(ans,sumPre-minPre)
minPre = min(minPre,sumPre)
return ans3.合并区间
关键点：现将intervals按左端点元素排序
需要引用sort的高阶操作
intervals.sort（key=lambda p:p0）
lambda 匿名函数免去函数命名
p是待排序列表中的【每一个元素】 针对这个题就是每一个区间
p0那就是区间第一个元素
需要做的判断1.如果ans空，就先append进去
2.此时ans的-11就是区间的右端点，需要拿他和下一个进入的区间的左端点p0比较
如果比他小，那就说明两个区间不相交，直接append
r如果比他大，那就说明有相交，那就更新最后一个合并区间的右端点为两者的最大值
举例子直观理解
假设 intervals 排序后为 [[1,3],[2,6],[8,10]]，执行过程：
-
处理第一个区间
[1,3]：ans为空，直接append([1,3])→ans = [[1,3]]；ans[-1][1]=3（最后一个区间的右端点）。
-
处理第二个区间
[2,6]：- 判断
p[0]=2 ≤ ans[-1][1]=3→ 重叠，需要合并； - 更新
ans[-1][1] = max(3,6) = 6→ans = [[1,6]]； - 此时
ans[-1][1] = 6。
- 判断
-
处理第三个区间
[8,10]：- 判断
p[0]=8 > ans[-1][1]=6→ 不重叠； append([8,10])→ans = [[1,6],[8,10]]；- 此时
ans[-1][1] = 10。
- 判断
最终 ans 就是合并后的结果 [[1,6],[8,10]]。
时间复杂度：sort的时间 空间复杂度1
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
intervals.sort(key=lambda p:p[0])
ans = []
for p in intervals:
if ans and p[0] <= ans[-1][1]:
ans[-1][1] = max(ans[-1][1],p[1])#更新右端点
else:
ans.append(p)
return ans