AI导读AI论文:mHC: Manifold-Constrained Hyper-Connections

文档核心总结

本文提出Manifold-Constrained Hyper-Connections（mHC），旨在解决Hyper-Connections（HC）扩展残差流宽度时破坏恒等映射、导致训练不稳定与内存开销过大的问题。mHC通过流形约束恢复恒等映射属性，结合基础设施优化，在大规模LLM预训练中实现性能、稳定性与效率的平衡。

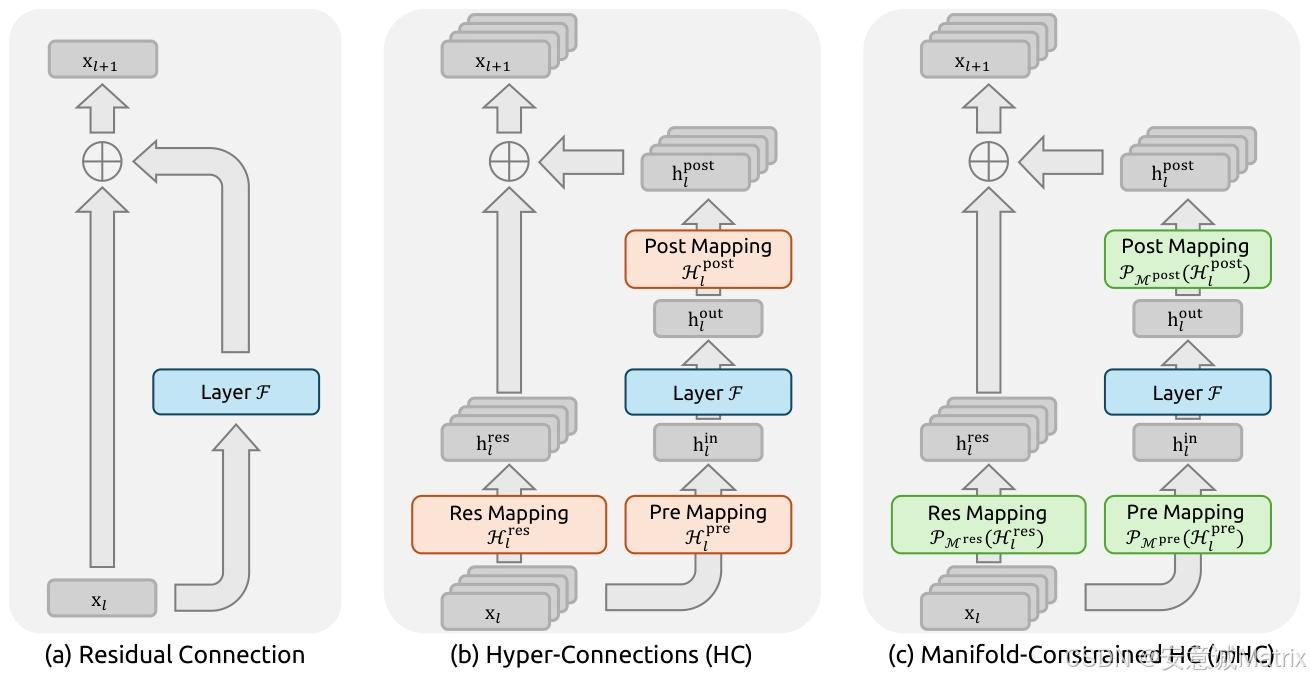
一、研究背景与核心问题

1. 残差连接的基础地位

自ResNet（He et al., 2016a）提出以来，残差连接成为深度学习（尤其是LLM）的核心设计，其核心优势是恒等映射属性------保障信号在深层网络中稳定传播。

标准残差连接单层公式（行内格式）：xl+1=xl+F(xl,Wl)x_{l+1} = x_l + \mathcal{F}(x_l, \mathcal{W}_l)xl+1=xl+F(xl,Wl)
多层递归扩展（独立公式）：
xL=xl+∑i=lL−1F(xi,Wi) x_L = x_l + \sum_{i=l}^{L-1} \mathcal{F}(x_i, \mathcal{W}_i) xL=xl+i=l∑L−1F(xi,Wi)
其中xlx_lxl为浅层输入，直接无修改传递至深层xLx_LxL，是大规模训练稳定的关键。

2. HC的创新与局限

HC（Zhu et al., 2024）通过扩展残差流宽度 （从CCC维增至n×Cn \times Cn×C维）和多样化连接，提升拓扑复杂度但不增加单单元FLOPs：

HC单层传播公式：
xl+1=Hlresxl+Hlpost⊤F(Hlprexl,Wl) x_{l+1} = \mathcal{H}_l^{res} x_l + \mathcal{H}_l^{post\top} \mathcal{F}(\mathcal{H}_l^{pre} x_l, \mathcal{W}_l) xl+1=Hlresxl+Hlpost⊤F(Hlprexl,Wl)

其中Hlpre∈R1×n\mathcal{H}_l^{pre} \in \mathbb{R}^{1 \times n}Hlpre∈R1×n（流聚合）、Hlpost∈R1×n\mathcal{H}_l^{post} \in \mathbb{R}^{1 \times n}Hlpost∈R1×n（流映射回）、Hlres∈Rn×n\mathcal{H}_l^{res} \in \mathbb{R}^{n \times n}Hlres∈Rn×n（流内混合）。
HC的两大核心问题：
1. 训练不稳定性 ：多层层叠后，复合映射∏i=1L−lHL−ires\prod_{i=1}^{L-l} \mathcal{H}_{L-i}^{res}∏i=1L−lHL−ires破坏特征全局均值，导致信号爆炸/衰减（27B模型中Amax增益峰值达3000）；
2. 系统开销大 ：nnn倍残差流使内存访问成本增至(5n+1)C+n2+2n(5n+1)C + n^2 + 2n(5n+1)C+n2+2n（远高于标准残差连接的2C2C2C），管道通信成本增nnn倍。

二、mHC核心方法

mHC的核心是流形约束+基础设施优化，既恢复恒等映射，又控制开销。

1. 流形约束：双重随机矩阵

将Hlres\mathcal{H}l^{res}Hlres投影到双重随机矩阵流形（Birkhoff多面体） ，定义为：
PMres(Hlres):={Hlres∈Rn×n∣Hlres1n=1n, 1n⊤Hlres=1n⊤, Hlres≥0} \mathcal{P}{\mathcal{M}^{res}}(\mathcal{H}_l^{res}) := \left\{ \mathcal{H}_l^{res} \in \mathbb{R}^{n \times n} \mid \mathcal{H}_l^{res} 1_n = 1_n, \, 1_n^\top \mathcal{H}_l^{res} = 1_n^\top, \, \mathcal{H}_l^{res} \geq 0 \right\} PMres(Hlres):={Hlres∈Rn×n∣Hlres1n=1n,1n⊤Hlres=1n⊤,Hlres≥0}

关键特性：n=1n=1n=1时退化为恒等映射；具备三大优势：
1. 范数保持：谱范数∥Hlres∥2≤1\| \mathcal{H}_l^{res} \|_2 \leq 1∥Hlres∥2≤1，避免梯度爆炸；
2. 复合封闭：多矩阵相乘仍为双重随机，全模型深度稳定；
3. 凸包解释：是置换矩阵的凸包，实现流间信息单调混合。

2. 参数化与流形投影

输入预处理：将xl∈Rn×Cx_l \in \mathbb{R}^{n \times C}xl∈Rn×C展平为x⃗l=vec(xl)∈R1×nC\vec{x}_l = vec(x_l) \in \mathbb{R}^{1 \times nC}x l=vec(xl)∈R1×nC，应用RMSNorm；
映射计算（动态+静态）：
{x⃗l′=RMSNorm(x⃗l)H~lpre=αlpre⋅(x⃗l′φlpre)+blpreH~lpost=αlpost⋅(x⃗l′φlpost)+blpostH~lres=αlres⋅mat(x⃗l′φlres)+blres \left\{ \begin{aligned} \vec{x}_l' &= RMSNorm(\vec{x}_l) \\ \tilde{\mathcal{H}}_l^{pre} &= \alpha_l^{pre} \cdot (\vec{x}_l' \varphi_l^{pre}) + b_l^{pre} \\ \tilde{\mathcal{H}}_l^{post} &= \alpha_l^{post} \cdot (\vec{x}_l' \varphi_l^{post}) + b_l^{post} \\ \tilde{\mathcal{H}}_l^{res} &= \alpha_l^{res} \cdot mat(\vec{x}_l' \varphi_l^{res}) + b_l^{res} \end{aligned} \right. ⎩ ⎨ ⎧x l′H~lpreH~lpostH~lres=RMSNorm(x l)=αlpre⋅(x l′φlpre)+blpre=αlpost⋅(x l′φlpost)+blpost=αlres⋅mat(x l′φlres)+blres
约束施加：
{Hlpre=σ(H~lpre)Hlpost=2σ(H~lpost)Hlres=Sinkhorn-Knopp(H~lres) \left\{ \begin{aligned} \mathcal{H}_l^{pre} &= \sigma(\tilde{\mathcal{H}}_l^{pre}) \\ \mathcal{H}_l^{post} &= 2\sigma(\tilde{\mathcal{H}}_l^{post}) \\ \mathcal{H}_l^{res} &= \text{Sinkhorn-Knopp}(\tilde{\mathcal{H}}_l^{res}) \end{aligned} \right. ⎩ ⎨ ⎧HlpreHlpostHlres=σ(H~lpre)=2σ(H~lpost)=Sinkhorn-Knopp(H~lres)
其中σ\sigmaσ为Sigmoid，Sinkhorn-Knopp算法通过迭代归一化收敛至双重随机矩阵：
M(t)=Tr(Tc(M(t−1))),M(0)=exp⁡(H~lres) M^{(t)} = \mathcal{T}_r\left( \mathcal{T}_c(M^{(t-1)}) \right), \quad M^{(0)} = \exp(\tilde{\mathcal{H}}l^{res}) M(t)=Tr(Tc(M(t−1))),M(0)=exp(H~lres)
实验中设迭代次数tmax=20t{max}=20tmax=20。

3. 基础设施优化（控制开销）

核融合 ：混合精度+操作融合，将Hpre/post/res\mathcal{H}{pre/post/res}Hpre/post/res计算、残差合并等融合为统一核，Fpost,res\mathcal{F}{post,res}Fpost,res核读写量大幅下降；
选择性重计算 ：丢弃中间激活，反向重算，最优块大小为：
Lr∗=arg⁡min⁡Lr[nC×⌈LLr⌉+(n+2)C×Lr]≈nLn+2 L_r^* = \arg\min_{L_r} \left[ nC \times \left\lceil \frac{L}{L_r} \right\rceil + (n+2)C \times L_r \right] \approx \sqrt{\frac{nL}{n+2}} Lr∗=argLrmin[nC×⌈LrL⌉+(n+2)C×Lr]≈n+2nL
DualPipe通信重叠 ：高优先级计算流+避免持久核，减少nnn流带来的通信延迟。

三、实验验证

1. 实验设置

模型规模：3B/9B/27B/3B 1T Tokens（MoE架构，DeepSeek-V3）；
关键参数：扩展率n=4n=4n=4，AdamW优化器，Sinkhorn-Knopp tmax=20t_{max}=20tmax=20；
对比对象：基线（标准残差连接）、HC；下游任务覆盖推理（BBH、GSM8K）、阅读理解（DROP）等8项。

2. 核心结果

稳定性：27B模型中，mHC无HC的12k步损失骤升问题，梯度norm稳定，较基线损失降低0.021；
性能：mHC在所有任务中优于基线，多数优于HC（表1）：

表1 | 27B模型下游任务性能（关键指标）

任务 BBH(3-shot EM) DROP(3-shot F1) GSM8K(8-shot EM) MMLU(5-shot Acc.)

基线 43.8 47.0 46.7 59.0

HC 48.9 51.6 53.2 63.0

mHC 51.0 53.9 53.8 63.4
效率：n=4n=4n=4时仅引入6.7%的额外时间开销；
扩展性：3B→9B→27B模型中，mHC性能优势持续保持；3B 1T Tokens训练中，损失稳定下降。

任务	BBH(3-shot EM)	DROP(3-shot F1)	GSM8K(8-shot EM)	MMLU(5-shot Acc.)
基线	43.8	47.0	46.7	59.0
HC	48.9	51.6	53.2	63.0
mHC	51.0	53.9	53.8	63.4

3. 稳定性量化

mHC的Amax增益较HC大幅降低：

复合映射最大Amax增益≈1.6（较HC的3000降低3个数量级），信号传播稳定。

四、结论与展望

核心结论：mHC通过双重随机矩阵流形约束恢复恒等映射，结合核融合、重计算、通信重叠优化，在27B模型上实现性能提升、稳定性增强、效率平衡（6.7%额外开销）；
未来方向：探索更多定制化流形约束，深化宏观架构设计研究，为下一代基础模型拓扑优化提供新方向。