论文: The Entropy Mechanism of Reinforcement Learning for Reasoning Language Models
0. 摘要原文翻译
本文旨在克服扩大强化学习(RL)规模以用于大语言模型(LLMs)推理时的一个主要障碍,即策略熵的坍塌(collapse of policy entropy) 。这种现象在未进行熵干预的大规模RL运行中被持续观察到:策略熵在训练早期急剧下降,导致策略模型过于自信 。结果是,这种探索能力的减弱总是伴随着策略性能的饱和。
在实践中,我们建立了熵 H \mathcal{H} H 与下游性能 R R R 之间的变换方程 R = − a exp ( H ) + b R = -a \exp(\mathcal{H}) + b R=−aexp(H)+b,其中 a , b a, b a,b 为拟合系数 。这一经验定律强烈表明,策略性能是以牺牲策略熵为代价换取的,因此受到熵耗尽的瓶颈限制,且上限是完全可预测的(当 H = 0 \mathcal{H}=0 H=0 时, R ≈ − a + b R \approx -a+b R≈−a+b)。
我们的发现使得为了通过扩大计算规模进行RL持续探索,必须进行熵管理。为此,我们在理论和经验上研究了熵的动力学。我们的推导强调,策略熵的变化是由动作概率与logits变化之间的协方差驱动的,在使用类策略梯度算法(Policy Gradient-like)时,这与优势(Advantage)成正比 。也就是说,具有高优势的高概率动作会降低策略熵,而具有高优势的罕见动作会增加策略熵 。
经验研究表明,协方差项的值与熵的差值完全匹配,支持了理论结论 。此外,协方差项在训练过程中大多保持正值,进一步解释了为什么策略熵会单调递减。通过理解熵动力学背后的机制,我们提出通过限制高协方差Token 的更新来控制熵 。具体来说,我们提出了两种简单而有效的技术,即 Clip-Cov 和 KL-Cov,分别对具有高协方差的Token进行截断(Clip)和施加KL惩罚 。实验表明,这些方法鼓励了探索,从而帮助策略摆脱熵坍塌并实现更好的下游性能
1. 方法动机 (Motivation)
a) 背景与驱动力
随着RL(如Reinforcement Learning from Verifiable Rewards)被广泛应用于提升LLM的推理能力(如数学、代码任务),人们希望通过扩大训练计算规模(Scaling Laws)来获得更强的模型性能。
b) 现有痛点与局限性
- 熵坍塌(Entropy Collapse): 作者观察到一个普遍现象:RL训练初期,策略熵会迅速下降至接近0。模型变得极度"确信",失去了探索新路径的能力。
- 性能饱和与可预测性: 随着熵的消失,模型性能迅速达到瓶颈。论文发现性能 R R R 和熵 H \mathcal{H} H 之间存在严格的指数关系,意味着一旦熵耗尽,性能也就封顶了。
- 传统正则化失效: 简单的熵正则化(Entropy Loss)或全局KL惩罚往往无效,要么导致熵爆炸,要么损害性能。
c) 核心研究假设
策略熵的减少是由某些特定的Token驱动的,这些Token既有高概率(模型自信)又有高优势(高奖励)。如果我们能精准地抑制这些"过度自信且高回报"的Token的更新幅度,就能在不伤害整体学习的前提下维持探索能力。
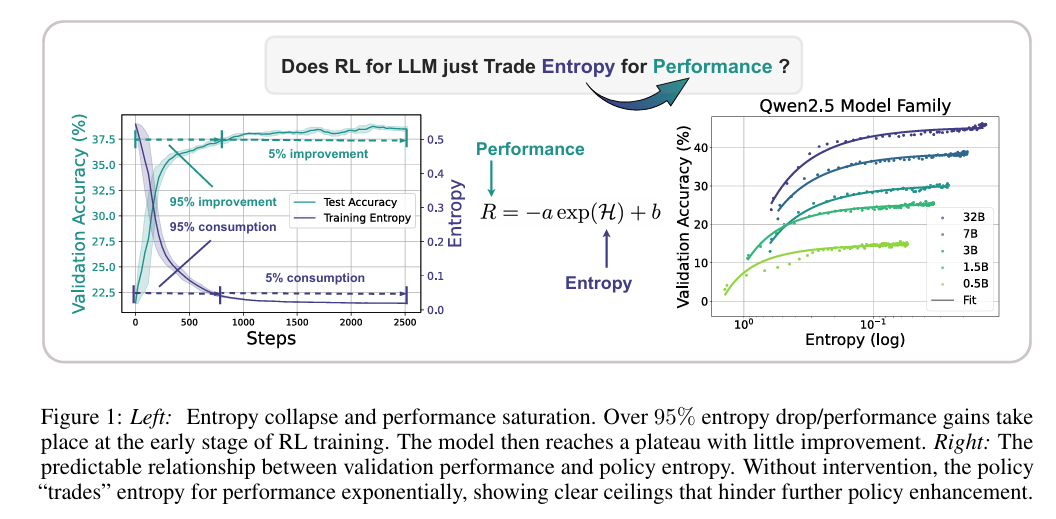
如图所示,作者的实验结果发现能拟合一条曲线;同时,训练初期,熵就迅速坍塌,随后模型性能提升进入平坦区域,只有微小的5%的提升。
ThePredictable "Collapse" of Policy Entropy

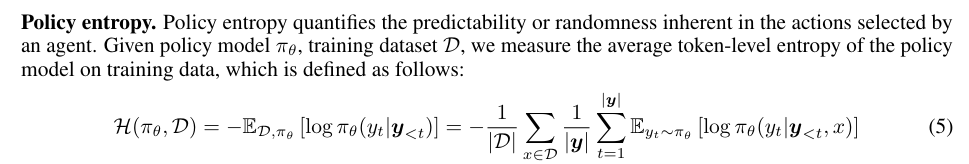
受到熵坍塌现象的启发,作者发现下游任务的表现(accuracy)和熵的关系可以用以下曲线来拟合:
R = − a e p x ( H ) + b R=-a epx(H)+b R=−aepx(H)+b
其中,R代表验证集的表现,H是熵。
作者的实验结果如下:
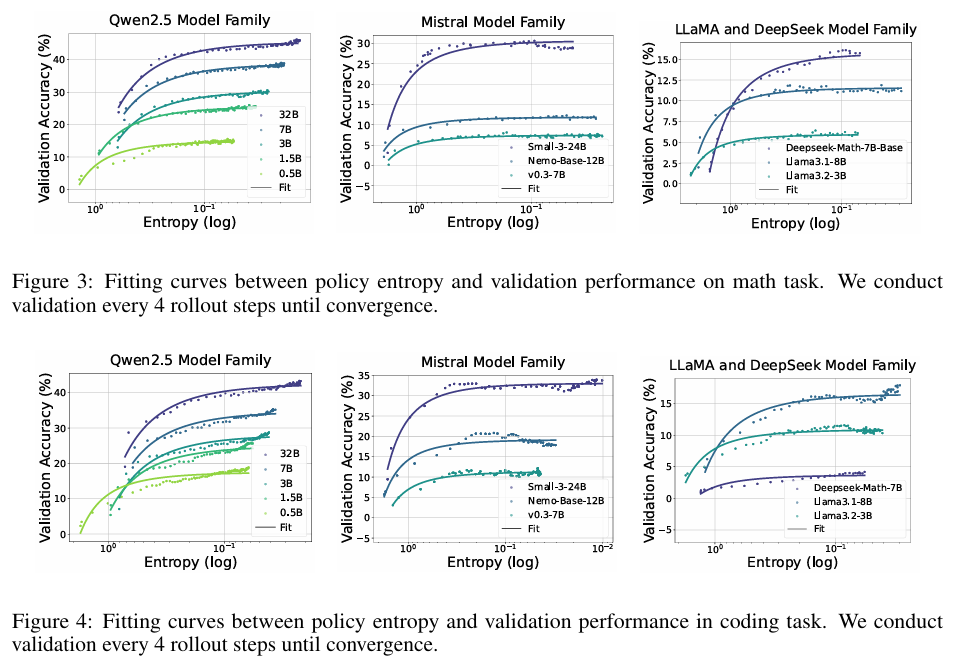
根据这个公式,我们就可以在高熵下采样若干个数据点来拟合曲线,从而去预测低熵下的模型性能,作者进一步做了实验验证,这种预测的误差精度很低,预测的准确性很高。
同时,对于 RL是否只是激活了模型预训练阶段所学习的知识,从而无法突破模型的上限这个问题,作者的实验结果显然是支持这个观点的。根据这个公式,当熵很低的时候(为0),模型的上限不仅存在,还能被预测到。
2. 方法设计 (Methodology)
作者首先通过理论推导建立了熵变化与协方差的关系,基于此设计了两种正则化方法。
a) 理论基础:熵动力学
对于Softmax策略(如LLMs),在策略梯度(PG)更新下,一步之内熵的变化量 Δ H \Delta \mathcal{H} ΔH 近似等于:
H ( π θ k + 1 ) − H ( π θ k ) ≈ − η ⋅ C o v ( log π θ ( a ∣ s ) , π θ ( a ∣ s ) ⋅ A ( s , a ) ) \mathcal{H}(\pi_{\theta}^{k+1}) - \mathcal{H}(\pi_{\theta}^{k}) \approx -\eta \cdot Cov( \log \pi_{\theta}(a|s), \pi_{\theta}(a|s) \cdot A(s,a) ) H(πθk+1)−H(πθk)≈−η⋅Cov(logπθ(a∣s),πθ(a∣s)⋅A(s,a))
通俗解释 :如果模型对某个动作 a a a 赋予了高概率( log π \log \pi logπ 大),且该动作的优势 A A A 也很大(是个好动作),那么这个协方差项就是正的,导致熵 H \mathcal{H} H 减小。反之,如果高优势对应的是低概率动作(罕见动作),熵会增加。
b) 核心Pipeline (算法流程)
Step 1: 数据采样与优势计算
-
对于输入Prompt x x x,模型生成回复 y y y。
-
cite_start\]使用GRPO等算法计算每个Token的优势 A t A_t At \[cite: 131-133\]。
-
根据理论推导,定义每个Token的中心化叉积(Centered Cross-Product),作为协方差的估计值:
C o v ( y i ) = ( log π θ ( y i ) − log π ‾ ) ⋅ ( A ( y i ) − A ‾ ) Cov(y_i) = ( \log \pi_{\theta}(y_i) - \overline{\log \pi} ) \cdot ( A(y_i) - \overline{A} ) Cov(yi)=(logπθ(yi)−logπ)⋅(A(yi)−A) -
这里 N N N 是Batch内的Token总数, ⋅ ‾ \overline{\cdot} ⋅ 表示均值 。
Step 3: 筛选高协方差Token
- 数据分析发现,极少数(如Top 0.02%)的Token贡献了绝大部分的协方差值,这些是导致熵坍塌的"罪魁祸首" 。
简单来说,"高协方差"的Token是指那些模型既对其非常有信心(概率高),同时它又确实获得了很高奖励(优势大)的Token。 在梯度更新时,这会促使模型大幅增加该Token的概率,从而导致概率分布迅速尖锐化,其他可能性的概率被压缩,导致策略熵(探索能力)急剧下降
正是因此这些高协方差的Token导致模型过早丧失探索能力,作者才提出了下面的两种方法。
但是在此之前,作者先用实验证明了一些早期的熵正则化的方法:
- 将熵作为Loss的一部分 L = L − α H ( π θ ) L = L − αH(π_θ) L=L−αH(πθ).
- 增加KL散度 L = L + β D K L ( π θ ∣ ∣ π r e f ) L=L+\beta \mathbb{D}{KL}(\pi\theta||\pi_{ref}) L=L+βDKL(πθ∣∣πref)
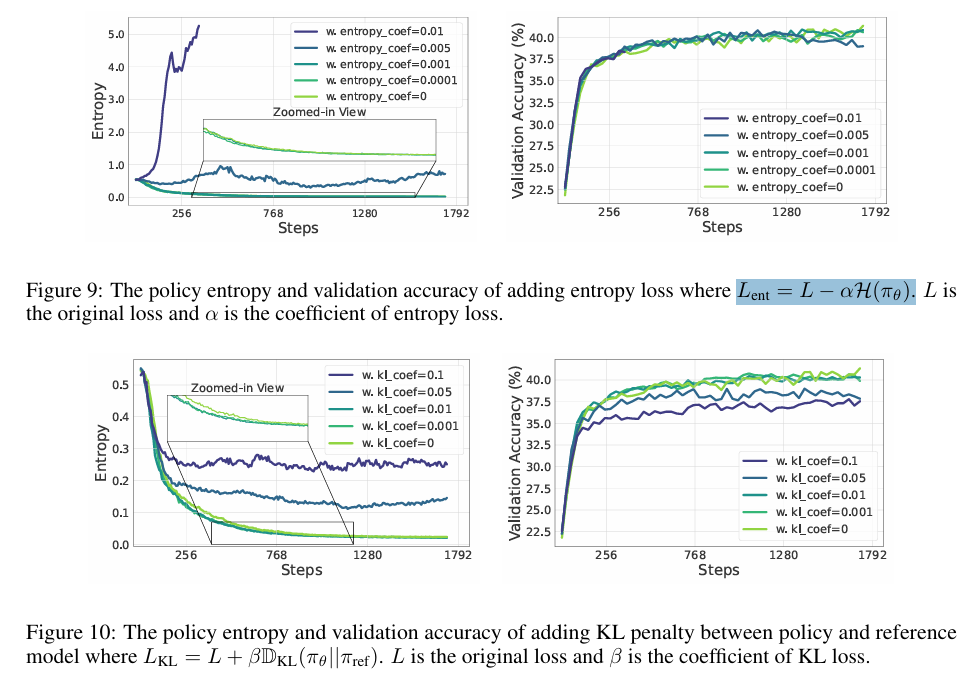
Step 4: 实施正则化策略 (二选一)
策略一:Clip-Cov (截断协方差)
- 操作: 随机选择一部分协方差值落在特定高区间 [ ω l o w , ω h i g h ] [\omega_{low}, \omega_{high}] [ωlow,ωhigh] 的Token。
- 处理: 将这些被选中Token的梯度切断(Detach),即在本次更新中忽略它们,防止模型在这些点上进一步"固化" 。
- 公式: L C l i p − C o v L_{Clip-Cov} LClip−Cov 仅计算未被选中Token的PG Loss。
策略二:KL-Cov (KL惩罚协方差)
- 操作: 对协方差值进行排序,选出Top- k k k(例如前0.2%)的Token。
- 处理: 对这些特定的Token施加额外的KL散度惩罚,迫使当前策略不要偏离参考策略太远。
- 公式:
L K L − C o v = L P G + β ∑ t ∈ I K L D K L ( π θ ∣ ∣ π r e f ) L_{KL-Cov} = L_{PG} + \beta \sum_{t \in I_{KL}} \mathbb{D}{KL}(\pi{\theta} || \pi_{ref}) LKL−Cov=LPG+βt∈IKL∑DKL(πθ∣∣πref)
c) 模块协同
这个设计并不改变RL的主体算法(如GRPO),而是作为一个插件嵌入在Loss计算环节。它充当了一个"减速带",专门针对那些让模型变得过于确信的样本点进行减速。
3. 与其他方法对比
a) 本质区别
- 传统方法 (Entropy Regularization/Global KL): 对所有Token"一视同仁"地施加惩罚或奖励。
- Clip-Higher (Baseline): 通过调整PPO Clip的上限阈值来增加探索,但这主要影响正优势样本,且不够精准 。
- 本方法 (Clip/KL-Cov): Token粒度的精准打击。只针对那些导致熵快速下降的"高协方差"Token进行干预 。
b) 优缺点对比
| 方法 | 核心机制 | 优点 | 缺点 |
|---|---|---|---|
| Entropy Loss | 在Loss中减去熵项 α H \alpha \mathcal{H} αH | 实现简单 | [cite_start]对超参极度敏感,易导致熵爆炸或无效 |
| Global KL | 全局施加KL惩罚 | 保证策略稳定性 | [cite_start]往往导致性能下降,无法有效提升探索 |
| Clip-Higher | 提高PPO Clip上限 ( ϵ \epsilon ϵ) | 早期能提升熵 | [cite_start]训练后期不稳定,性能容易饱和 |
| Clip-Cov (Ours) | 截断高协方差Token梯度 | 有效维持高熵,提升性能 | 需要调节截断比例和阈值 |
| KL-Cov (Ours) | 惩罚高协方差Token | 熵曲线更平稳,性能最佳 | 引入了KL系数超参 |
4. 实验表现与优势
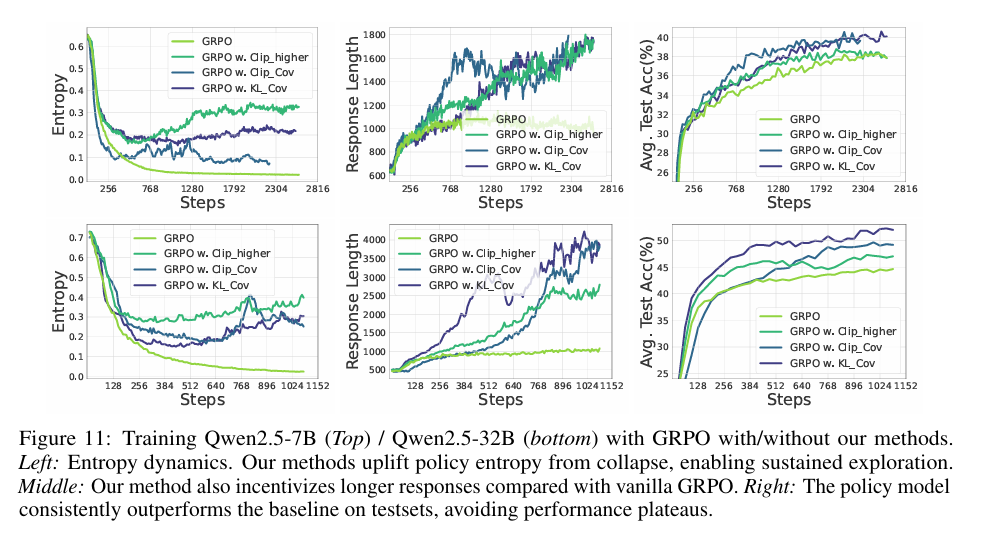
a) 实验设置
- 模型: Qwen2.5-7B 和 Qwen2.5-32B 。
- 任务: 数学推理(AIME, MATH-500, OlympiadBench等)。
- 算法: 基于GRPO进行改进 。
b) 关键实验数据
- 总体提升: 相比于基线GRPO,Qwen2.5-7B平均提升 2.0% ,Qwen2.5-32B平均提升 6.4% 。
- 高难度任务: 在AIME24上,32B模型使用KL-Cov相比GRPO提升了 15.0% (21.8% -> 36.8%) 。
- 熵保持: 当基线GRPO的熵降至接近0时,KL-Cov方法的熵仍保持在10倍以上的水平。
c) 优势场景
- 大规模模型: 在32B模型上的提升显著高于7B模型,说明该方法能释放大模型更强的潜在探索能力。
- 长链条推理: 实验发现该方法激励模型生成更长的回复(Response Length),意味着模型在进行更深度的思考和探索 。
d) 局限性
- 超参敏感: 干预的Token数量非常少( 10 − 3 10^{-3} 10−3级别),调节需要精细 。
- 最优熵值未知: 虽然维持了高熵,但目前尚不清楚具体的"最优熵值"是多少。
同时作者对比了不同超参数对熵的影响:
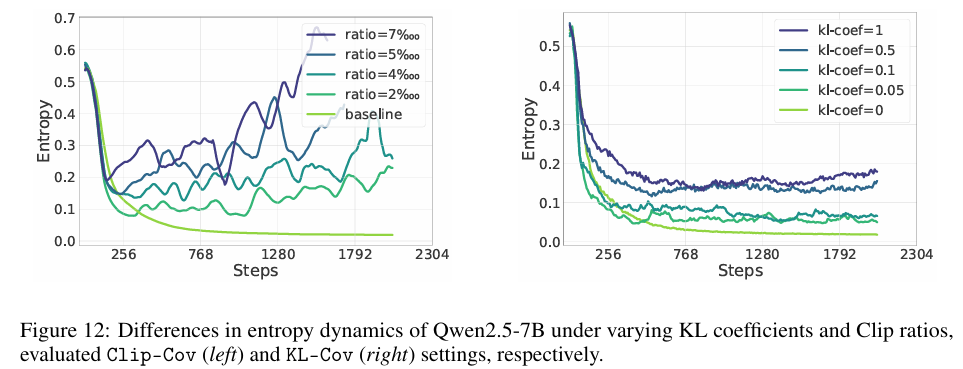
作者发现,可以通过简单的调整超参数的大小,来控制熵的增加,同时KL-cov的训练稳定性要好于Clip-cov。
6. 总结
a) 核心思想
RL中的熵坍塌是由极少数"高置信度且高奖励"的Token驱动的;通过Clip-Cov 或KL-Cov精准抑制这些Token的更新,可以强制模型保持探索能力,从而打破性能天花板。
b) 速记版Pipeline
- 算协方差 :计算每个Token的 ( log π − mean ) × ( A − mean ) (\log\pi - \text{mean}) \times (A - \text{mean}) (logπ−mean)×(A−mean)。
- 抓显眼包:找出协方差最高的极少数Token(Top 0.x%)。
- 精准打击:对这些Token进行梯度截断(Clip)或加KL惩罚。
- 正常更新:其余Token按原策略梯度算法更新。