Calibre nmDRC Dimensional Check Operations（ENClosure/EXTernal/INTernal）(16-1)

本文基于 Calibre v2017.1 官方手册，深度拆解 尺寸检查操作（Dimensional Check Operations） 的核心机制、三大核心操作（ENClosure/EXTernal/INTernal）、测量原理、度量标准及实战规则编写，助力用户精准实现间距、宽度、包围等关键 DRC 约束检查，覆盖先进工艺下的复杂几何验证需求。

一、维度检查概述与核心价值

尺寸检查操作是 Calibre nmDRC 设计规则检查功能的核心。这类操作通过测量单个或两个输入图层上的图形边缘间距，生成派生的错误图层 、边缘图层 或多边形图层 。

尺寸检查主要包含：

• 覆盖关键约束场景：间距（EXTernal）、宽度 / 重叠（INTernal）、包围 / 延伸（ENClosure）；

• 高精度测量：支持多种度量标准（Euclidean/Square 等），适配不同工艺的几何要求；

• 灵活输出：可生成错误层（违规标记）、边缘层（测量目标边缘）、多边形层（测量区域）；

• 兼容层级化模式：nmDRC-H 下支持层级化处理，避免重复计算。

二、三大核心维度检查操作

核心尺寸检查操作包含三种：包围检查（ENClosure） 、外部间距检查（EXTernal） 以及 内部尺寸检查（INTernal）。

• 包围检查：用于执行包围验证或延伸量验证。
• 外部间距检查：用于执行图形间的间距验证。
• 内部尺寸检查：用于执行图形宽度验证或图形重叠量验证。

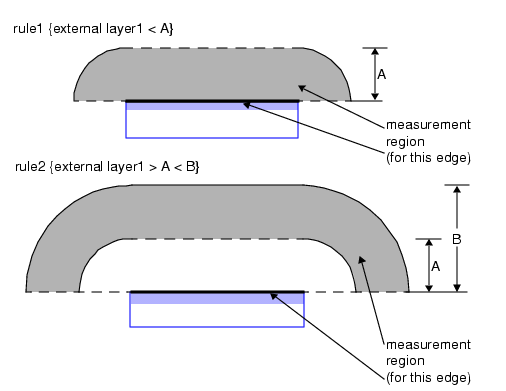
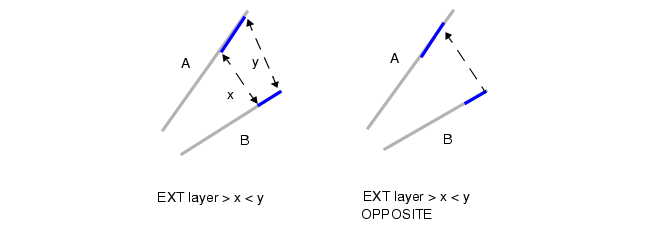
下图展示了尺寸检查操作所测量的图形边缘对象。

包围检查 仅支持双输入图层 的语法格式；而外部间距检查 和内部尺寸检查 同时支持单层 和双层语法格式。本示例中未使用完整的规则检查语法（即包含规则检查名称和外层大括号的完整格式）。

矩形包围检查（Rectangle Enclosure） 、相邻判定（[Not] With Neighbor） 、时序驱动型设计规则检查（TDDRC） 以及 可制造性设计测量（DFM Measure） 这四类操作，均基于上述三种核心尺寸检查操作实现。

尺寸检查操作，以及 SVRF 语言中的其他许多语句，都可以关联可选的次级关键字。这些次级关键字会影响其所在操作的运行逻辑。

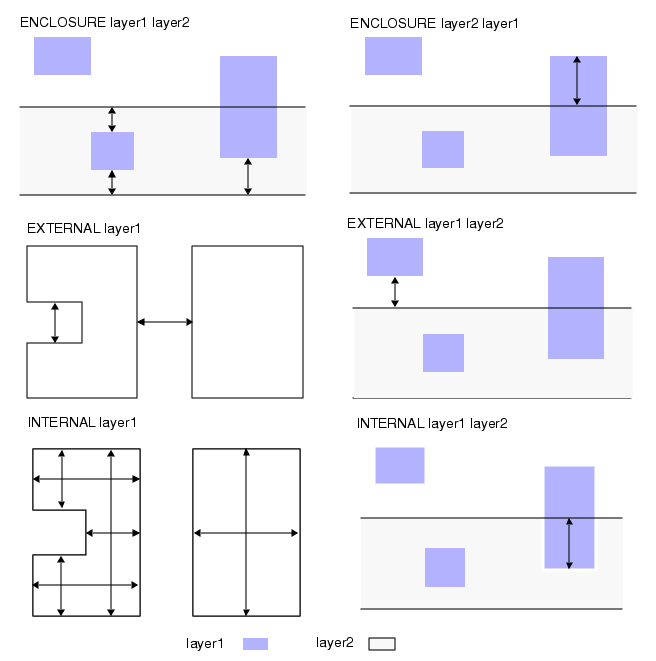
Figure 1. Measured Edges in the Dimensional Check Operations The Rectangle

维度检查包含三个基础操作，覆盖绝大多数 DRC 约束场景，其核心用途、语法及适用场景如下：

操作名称	核心用途	支持图层模式	典型应用场景
EXTernal（EXT）	间距检查（边缘间距离）	单图层（同层间距）、双图层（异层间距）	金属层同层间距、Poly 与 Active 异层间距
INTernal（INT）	宽度检查、重叠检查	单图层（宽度）、双图层（重叠）	金属线宽度、Poly 覆盖 Active 的重叠区域
ENClosure（ENC）	包围检查、延伸检查	仅双图层	Active 被 Poly 包围、金属线延伸超出接触孔

三、关键测量方式

3.1 边缘测量

尺寸检查操作输出的边缘对，仅包含被测边缘中满足测量约束条件的部分。这种边缘测量方法的执行流程如下（参考图 6-2）。

假设本次测量的对象是边缘 A 外侧到边缘 B 外侧的间距，且操作设定的规则为：输出间距小于 0.3 微米的边缘对。程序采用欧几里得度量法，通过构建两个区域来完成对边缘 A 和边缘 B 的测量：

1. 第一个区域为边缘 A 外侧半平面内，所有与边缘 A 间距不超过 0.3 微米的点的集合。

2. 第二个区域为边缘 B 外侧半平面内，所有与边缘 B 间距不超过 0.3 微米的点的集合。（工具默认的长度单位为微米）

最终输出的边缘对包含两部分：一是边缘 A 中与边缘 B 对应区域相交的线段，二是边缘 B 中与边缘 A 对应区域相交的线段。该操作仅输出被测边缘中，实际满足尺寸检查约束条件的部分。

本示例采用的约束条件为 "小于 0.3 微米"，其他所有合法的约束条件或数值的执行逻辑均与之类似。

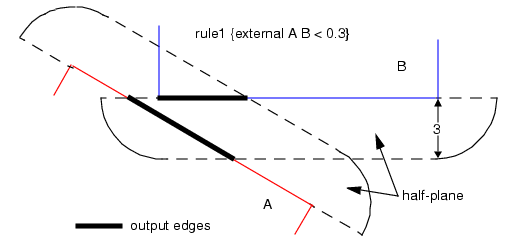
Figure 2. Euclidean Generation of Output Edges

3.2 测量区域构建

在为一条边缘构建测量区域时，程序会根据操作的设定，在该边缘的外侧或内侧 形成一个边界。这个区域被称为半平面。

该边界的形状，部分由操作约束条件中的数值决定。边界由半平面内所有与被测边缘间距等于约束数值的点构成。

根据操作约束条件的不同，半平面内由边界围合的测量区域的构成方式也不同，具体规则如下：

1. 若约束条件的形式为 x < a，则测量区域为边界内侧的所有点。

2. 若约束条件的形式为 x <= a，则测量区域为边界内侧及边界本身的所有点。

3. 若约束条件的形式为 x == a，则测量区域仅包含边界本身。

4. 若约束条件的形式为 a < x < b，则测量区域为半径为 a 的边界外侧 ，且半径为 b 的边界内侧 的所有点。其余三种合法的约束形式（a <= x < b、a < x <= b、a <= x <= b），则会将半径为 a 或 b 的边界包含在内。

Figure 3. Measurement Region Formation

第一个区域基于约束条件 x < a 构建，第二个区域基于约束条件 a < x <= b 构建。需要注意的是，包含边缘 A 的直线上的所有点，均不属于测量区域。

3.3 度量法

尺寸检查操作支持四种标准的度量法：欧几里得度量法（Euclidean） 、直角度量法（Square） 、反向直角度量法（Opposite） 以及 扩展反向直角度量法（Opposite Extended）。

1. 欧几里得度量法 ：构建的测量区域边界为圆角，边界会延伸至被测边缘的端点外侧。这是默认的度量法，在图层操作中无需额外指定关键字。

2. 直角度量法 ：构建的测量区域边界为直角，边界会延伸至被测边缘的端点外侧。

3. 反向直角度量法 ：构建的测量区域边界为直角 ，边界不会延伸至被测边缘的端点外侧。

4. 扩展反向直角度量法 ：构建的测量区域边界为直角 ，边界是否延伸至被测边缘的端点外侧，取决于用户指定的扩展值 。这种度量法支持非对称测量------ 即从边缘 A 到边缘 B 的测量结果，与从边缘 B 到边缘 A 的测量结果可能不同。该度量法指定的扩展值必须为正数。

度量法仅决定边缘周围测量区域的边界构建方式，测量和输出流程的其他所有环节均保持不变。除欧几里得度量法外，其他三种度量法均通过尺寸检查操作的次级关键字进行配置。

对于反向类度量法（所有名称中包含 "Opposite" 的度量法），存在以下特殊处理规则：

• 约束条件 a <= x < b 会被等效为 a < x < b

• 约束条件 a <= x <= b 会被等效为 a < x <= b但上述等效规则在设计规则边界内曲线的上部存在无限相交的情况下不适用。

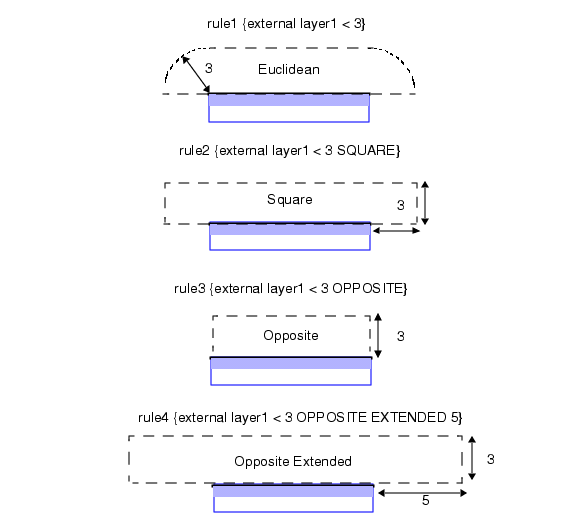
Figure 4. Measurement Regions for Basic Metrics

度量标准决定测量区域的边界形状，直接影响测量结果，核心差异如下：

度量标准	边界形状	是否延伸过拐角	适用场景	语法关键字
Euclidean（默认）	半圆边界（曲线）	是	大多数间距 / 宽度检查（模拟真实物理距离）	无（默认）
Square	直角边界（折线）	是	需严格按坐标轴方向测量的场景	SQUARE
Opposite	直角边界（折线）	否	避免拐角延伸导致的虚假测量	OPPOSITE
Opposite Extended value	直角边界（折线）	是（可指定延伸量）	非对称测量（A→B 与 B→A 结果不同）	OPPOSITE EXTENDED <value>

度量标准可视化对比（以 EXT 操作为例）

度量标准	边界形状示意图	关键特征
Euclidean	边缘两侧为半圆，拐角处为四分之一圆	最贴近真实物理距离，默认首选
Square	边缘两侧为矩形，拐角处延伸为直角	测量范围更大，适用于宽松约束
Opposite	边缘两侧为矩形，拐角处不延伸	测量范围精准，避免拐角干扰
Opposite Extended 0.1	边缘两侧为矩形，拐角处延伸 0.1um	可自定义延伸量，适配特殊工艺

四. 度量法拆分细节

4.1 Special Considerations for the Opposite Metric

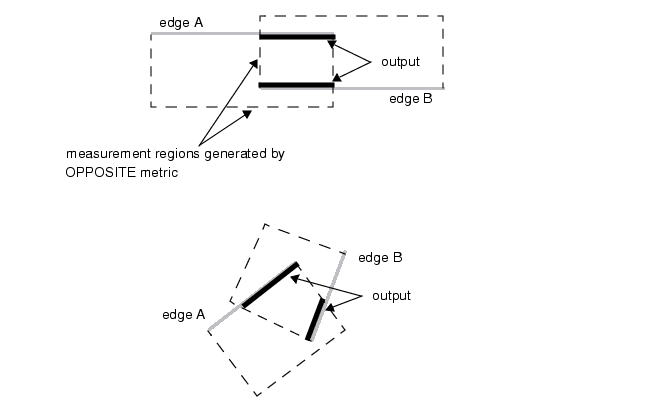
反向度量法（Opposite metric）的核心用途，是减少在使用多边形导向输出 （即 REGION 关键字输出）时产生的非正交边缘（相对于数据库坐标轴）数量。

首先，仅当满足以下两个条件时，反向度量法才会生成输出：

• 从边缘 A 到边缘 B 的测量区域与边缘 B 存在一个以上的交点
• 从边缘 B 到边缘 A 的测量区域与边缘 A 存在一个以上的交点具体如图 6-5 所示。

当反向度量法的两个测量区域均与对应边缘存在非平凡相交 时，这种测量被定义为可交换测量。

图 5 可交换测量

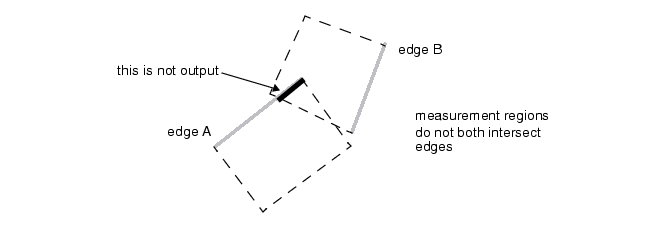
若两条边缘既不平行、也不与数据库坐标轴正交，就可能产生不可交换测量 ，具体如图 6-6 所示。在这种情况下，或任何产生不可交换测量的场景中，反向度量法不会生成任何输出。

图 6 不可交换测量

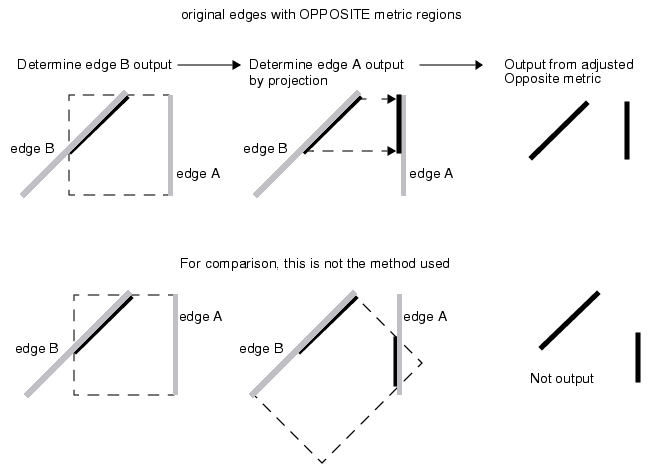
其次，若被测的两条边缘中恰好有一条 为非正交边缘（相对于数据库坐标轴），则测量区域仅基于正交边缘构建。

假设存在两条边缘 A 和 B，其中 B 为非正交边缘。此时边缘 B 会与基于边缘 A 构建的测量区域相交，进而从边缘 B 生成输出结果。而边缘 A 的输出结果，则是边缘 B 的输出结果在边缘 A 上的投影，具体如图 6-7 所示。

图 6-7 反向度量法的输出调整规则直观上可能会认为这种场景的输出结果应如图中第二组图形所示，但实际并非如此。第一组图形才是最终的输出形式。

4.2 Advanced Metrics for Specialized Applications

某些专用度量法主要用于光学邻近效应校正（OPC） 和掩膜数据制备流程。这类度量法通常不用于常规的设计规则检查（DRC），但偶尔也能在这类场景中发挥作用。

第一类专用度量法是反向对称度量法，其详细说明见下文 "反向对称度量法" 章节。

• 反向对称度量法（Opposite Symmetric） ：除了具备反向度量法的功能外，该度量法还针对不相交、不垂直且不平行的边缘，提供特殊的处理逻辑。

• 反向填充对称度量法（Opposite FSymmetric） ：与反向对称度量法类似，额外增加了对反向对称度量法输出的不连续边缘进行填充的功能。

• 扩展反向对称度量法（Opposite Extended Symmetric value） ：与反向对称度量法类似，但改用扩展反向测量区域进行计算。

• 扩展反向填充对称度量法（Opposite Extended FSymmetric value） ：与反向填充对称度量法类似，但改用扩展反向测量区域进行计算。

第二类专用度量法是单向度量法。

• 单向反向 1 度量法（Opposite1） ：与反向对称度量法类似，但仅执行从第一个输入图层 到第二个输入图层的单向测量，不支持反向测量。该度量法仅适用于双输入图层的场景。

• 单向反向 2 度量法（Opposite2） ：与反向对称度量法类似，但仅执行从第二个输入图层 到第一个输入图层的单向测量，不支持反向测量。该度量法仅适用于双输入图层的场景。

• 扩展单向反向 1 度量法（Opposite Extended1 value） ：与扩展反向对称度量法类似，但仅执行从第一个输入图层 到第二个输入图层的单向测量，不支持反向测量。该度量法仅适用于双输入图层的场景。

• 扩展单向反向 2 度量法（Opposite Extended2 value） ：与扩展反向对称度量法类似，但仅执行从第二个输入图层 到第一个输入图层的单向测量，不支持反向测量。该度量法仅适用于双输入图层的场景。

最后一类专用度量法是直角正交度量法（Square Orthogonal Metric）。

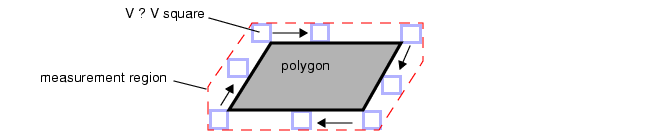
• 直角正交度量法（Square Orthogonal） ：该度量法模拟使用边长为（V×V）的正方形，沿着输入图层中每个多边形的周长进行环绕测量的效果。它适用于掩膜图层制备流程，可模拟掩膜在x 轴和 y 轴方向上的偏移误差。

4.3 Opposite Symmetric Metrics

反向对称度量法系列，基于反向度量法进行测量，并通过对输出结果的后处理 ，实现对非平行边缘的更优对称性优化。

反向对称度量法的执行步骤定义如下：

1. 给定边缘 A 和边缘 B，若二者平行、垂直或相交，则直接采用反向度量法进行计算，并按常规流程输出所有符合条件的结果。

2. 若二者不满足上述条件，仍采用反向度量法进行测量，但需跳过以下两个反向度量法的默认处理逻辑：

   • 跳过针对 "恰好有一条非正交边缘" 的特殊处理（详见 "反向度量法的特殊注意事项" 章节）

   • 即使测量结果为不可交换测量（见图 6-6），也不丢弃输出结果此步骤可能从每条边缘生成 0 个、1 个或 2 个输出结果。

3. 丢弃所有平凡输出边缘（详见 "平凡边缘" 章节）。由于反向度量法的特性，每条输入边缘最多只能生成一个输出边缘（即使使用区间约束）。

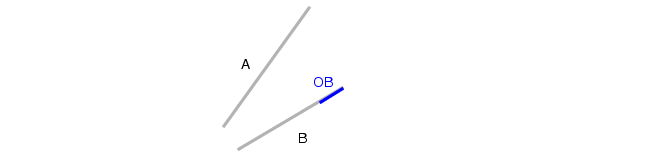
4. 若丢弃平凡边缘后，边缘 A 和边缘 B 均无输出结果，则直接终止流程且不生成任何输出；否则将最终的输出边缘命名为 OA（来自边缘 A）和 OB（来自边缘 B）。根据边缘的朝向和测量区域的大小，OA 或 OB 可能不存在。

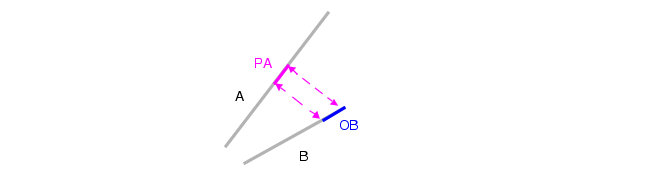
5. 若 OA 存在，则将其投影到边缘 B 上，形成线段 PB；若 OB 存在，则将其投影到边缘 A 上，形成线段 PA。若 PA 或 PB 是舍入误差导致的结果，则将其丢弃。

6. 生成边缘 A 的最终输出结果，即 OA 与 PA 的并集 ；生成边缘 B 的最终输出结果，即 OB 与 PB 的并集。

7. 若 OA 和 PA 均不存在，则边缘 A 无输出结果；若 OB 和 PB 均不存在，则边缘 B 无输出结果。

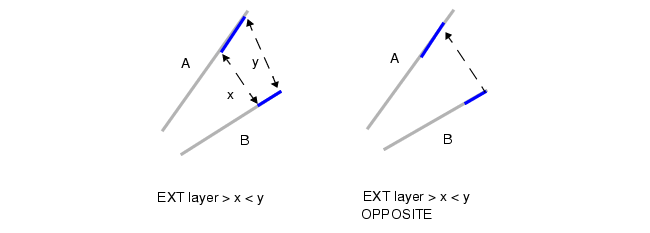
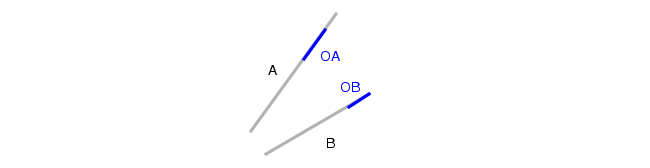
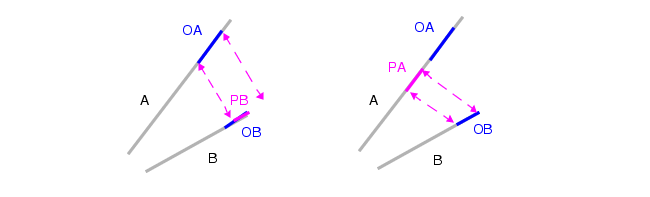
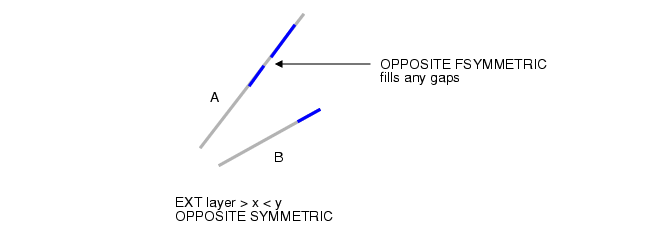
反向填充对称度量法（Opposite FSymmetric）对上述第 6 步进行了修改：将边缘 A 上位于 OA 与 PA 之间的所有部分，均并入 OA 与 PA 的并集中，最终从边缘 A 生成单一的输出边缘。边缘 B、OB 和 PB 的处理逻辑同理。详见下附图的注释说明。

扩展反向对称度量法（Opposite Extended Symmetric）的修改逻辑为：将上述算法第 1、2、3 步中的 "反向测量" 替换为 "扩展反向值测量"。

扩展反向填充对称度量法（Opposite Extended FSymmetric）的修改逻辑为：将上述算法第 1、2、3 步中的 "反向测量" 替换为 "扩展反向值测量"，同时按照反向填充对称度量法的规则修改第 6 步的处理逻辑。

4.4 Unidirectional Metrics

单向度量法系列，基于反向对称度量法的测量逻辑，但仅执行单一方向的测量 。这类度量法均假设输入为两个图层。

单向反向 1 度量法（Opposite1）的执行步骤定义如下：

1. 给定两条边缘，其中 A 来自图层 1，B 来自图层 2。若二者平行、垂直或相交，则直接采用反向度量法进行计算。

2. 若二者不满足上述条件，仍采用反向度量法进行测量，但需跳过以下两个反向度量法的默认处理逻辑：

   • 跳过针对 "恰好有一条非正交边缘" 的特殊处理（详见 "反向度量法的特殊注意事项" 章节）

   • 即使测量结果为不可交换测量（见图 6-6），也不丢弃输出结果此步骤可能从每条边缘生成 0 个、1 个或 2 个输出结果。

3. 丢弃所有平凡输出边缘 （详见 "平凡边缘" 章节）。由于反向度量法的特性，每条输入边缘与输出边缘之间存在一一对应的关系（即使使用区间约束）。

4. 丢弃第 2 步中所有与边缘 A 重合的输出结果（即仅保留与第二个输入图层 的边缘重合的输出结果）。若使用的是单向反向 2 度量法（OPPOSITE2），则此步骤的逻辑反转：仅保留与第一个输入图层的边缘重合的输出结果。后续步骤的测量方向也相应调整为从第二个输入图层到第一个输入图层。假设最终保留的输出边缘为 OB。

5. 将边缘 OB 投影到边缘 A 上，形成线段 PA。若 PA 为平凡线段，则将其丢弃。

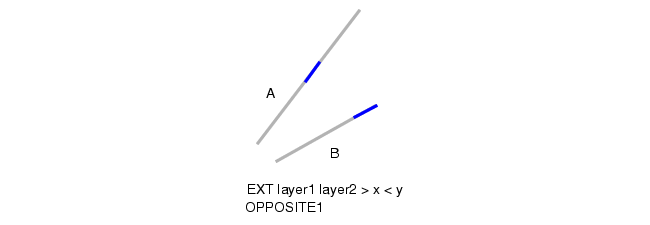
6. 生成边缘 A 的最终输出结果，即 PA ；生成边缘 B 的最终输出结果，即 OB。

最终输出结果详见图 8。

图 8 单向反向 1 度量法的输出结果

扩展单向反向对称度量法的修改逻辑为：将上述算法第 1、2、3 步中的 "反向测量" 替换为 "扩展反向值测量"。

4.5 Square Orthogonal Metric

在设计规则检查（DRC）的尺寸检查操作中 ------ 包括外部间距检查（EXTernal）、内部尺寸检查（INTernal）和包围检查（ENClosure），直角正交度量法（Square Orthogonal）可用于模拟掩膜在x 轴和 y 轴方向上同时发生偏移的效果。

以约束值为 V 的外部间距检查操作为例：

svrf

EXT layer < V ...

直角正交度量法的原理是：模拟使用边长为 V×V 的正方形，沿着输入图层中每个多边形的周长进行环绕测量。在环绕过程中，正方形的至少一个角始终与多边形保持接触；无论输入图层的边缘朝向如何，该正方形始终与数据库坐标轴保持正交。正方形环绕形成的路径，即为最终的测量区域。详见图 9。

图 9 直角正交测量区域

与其他所有度量法相同，直角正交度量法也必须遵循单条边缘的测量区域构建逻辑：

• 对于与数据库坐标轴正交的边缘，直角正交度量法与直角度量法（Square metric） 的效果完全等效。
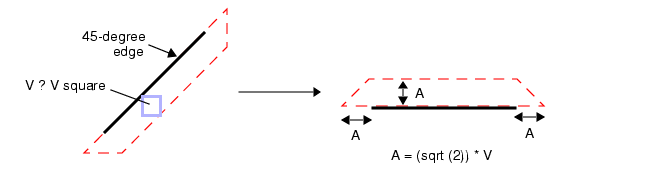
• 对于 45° 边缘，测量区域的形状为等腰梯形，其高为 A = (√2) × V（其中√为平方根函数）。梯形的长底边与 45° 边缘重合，长度为 45° 边缘的长度加上 2A。详见图 6-10。

图 10 45° 边缘的直角正交测量区域

对于与数据库坐标轴既不正交、也不成 45° 的多边形边缘（即斜向边缘），直角正交测量区域的构建过程更为复杂，通常需要由大量边缘线段组成的多边形链来拟合。

Calibre 并不支持由这类多边形链构成的测量区域构建逻辑，同时也希望避免为斜向边缘的测量区域构建定义过多的特殊场景。因此，斜向边缘的测量区域构建遵循以下原则：

1. 避免使用由大量边缘组成的多边形链
2. 为所有场景提供统一的算法逻辑
3. 尽可能逼近精确测量区域的形状
4. 能够平滑适配正交边缘和斜向边缘的极限情况

基于上述目标，斜向边缘的测量区域构建方法定义如下：

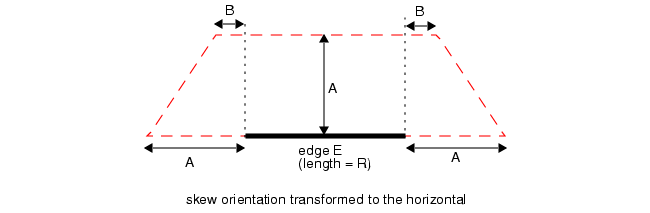
对于任意一条斜向边缘 E（见图 6-11），其端点坐标为 (x1, y1) 和 (x2, y2)，定义以下参数：

DX = |x2 - x1|
DY = |y2 - y1|
R = √(DX × DX + DY × DY)
A = V × R / max(DX, DY)
B = V × |DX - DY| / R

基于上述参数，构建一个等腰梯形，其尺寸定义如下：

• 斜向边缘 E 与梯形的底边 1重合
• 底边 1 的长度 = R + 2A
• 底边 2 的长度 = R + 2B
• 梯形的高 = A

图11 SQUARE ORTHOGONAL Measurement Region (Skew Edge)

四. 操作细节与实战示例

（1）EXTernal（EXT）：间距检查

核心逻辑：测量两个边缘（同层 / 异层）之间的距离，判断是否符合间距约束。

单图层模式（同层间距）

需求：Metal1 层同层边缘间距＜0.3um 时违规。

svrf

// 生成间距＜0.3um的错误层（Euclidean度量，默认）
met1_space_err = EXT MET1 < 0.3
// 完整规则
MET1_SPACING {
  met1_space_err = EXT MET1 < 0.3
  OUTPUT met1_space_err
  COMMENT "Metal1 minimum spacing: 0.3um"
}

双图层模式（异层间距）

需求：Poly 层与 Active 层边缘间距＜0.2um 时违规（Square 度量）。

svrf

// Square度量：直角边界，延伸过边缘拐角
poly_active_space_err = EXT POLY ACTIVE < 0.2 SQUARE
// 完整规则
POLY_ACTIVE_SPACING {
  poly_active_space_err = EXT POLY ACTIVE < 0.2 SQUARE
  OUTPUT poly_active_space_err
  COMMENT "Poly to Active minimum spacing: 0.2um"
}

（2）INTernal（INT）：宽度 / 重叠检查

核心逻辑：

• 单图层：测量边缘的 "内部宽度"（如线宽）；
• 双图层：测量两个图层的重叠区域（如 Poly 覆盖 Active 的面积）。

单图层模式（宽度检查）

需求：Metal2 层宽度＜0.4um 或＞2.0um 时违规（Opposite 度量）。

svrf

// Opposite度量：直角边界，不延伸过拐角
met2_width_err = INT MET2 < 0.4 OR > 2.0 OPPOSITE
// 完整规则
MET2_WIDTH {
  met2_width_err = INT MET2 < 0.4 OR > 2.0 OPPOSITE
  OUTPUT met2_width_err
  COMMENT "Metal2 width: 0.4um ~ 2.0um"
}

双图层模式（重叠检查）

需求：Poly 层与 Active 层重叠区域＜0.1um 时违规（确保 Poly 完全覆盖 Active）。

svrf

poly_active_overlap_err = INT POLY ACTIVE < 0.1
POLY_ACTIVE_OVERLAP {
  poly_active_overlap_err = INT POLY ACTIVE < 0.1
  OUTPUT poly_active_overlap_err
  COMMENT "Poly to Active minimum overlap: 0.1um"
}

（3）ENClosure（ENC）：包围 / 延伸检查

核心逻辑 ：仅双图层模式，检查input_layer1是否被input_layer2包围，或input_layer1是否延伸超出input_layer2。

包围检查

需求：Contact 孔必须被 Metal1 完全包围，Metal1 包围 Contact 的最小宽度＜0.15um 时违规。

svrf

// ENC：检查Contact（input1）被Metal1（input2）包围的宽度
contact_met1_enc_err = ENC CONTACT MET1 < 0.15
CONTACT_MET1_ENCLOSURE {
  contact_met1_enc_err = ENC CONTACT MET1 < 0.15
  OUTPUT contact_met1_enc_err
  COMMENT "Metal1 must enclose Contact by minimum 0.15um"
}

延伸检查

需求：Metal1 必须延伸超出 Contact 孔边缘至少 0.2um，延伸量＜0.2um 时违规。

svrf

// 延伸检查本质是包围检查的变种，约束延伸量
met1_contact_ext_err = ENC MET1 CONTACT < 0.2
MET1_CONTACT_EXTENSION {
  met1_contact_ext_err = ENC MET1 CONTACT < 0.2
  OUTPUT met1_contact_ext_err
  COMMENT "Metal1 must extend beyond Contact by 0.2um"
}

五、输出模式与虚假测量抑制

1. 输出模式（Output Modes）

维度检查支持三种输出模式，通过二级关键字指定：

输出模式	关键字	输出结果	适用场景
错误层（默认）	无	标记违规区域的错误层	DRC 违规检查
边缘层	EDGE	符合约束的边缘片段	边缘级分析（如缺口边缘提取）
多边形层	POLYGON	测量区域的多边形	区域级分析（如重叠区域可视化）

示例：输出边缘层

svrf

// 提取Metal1层宽度＜0.4um的边缘片段
met1_narrow_edge = INT MET1 < 0.4 EDGE
MET1_NARROW_EDGE {
  met1_narrow_edge = INT MET1 < 0.4 EDGE
  OUTPUT met1_narrow_edge
  COMMENT "Extract edges of Metal1 with width <0.4um"
}

2. 虚假测量抑制（False Measurement Reduction）

复杂几何图形（如锐角、小凸起）可能导致虚假测量（误报违规），可通过以下方式抑制：

• 最小长度过滤 ：使用MIN LENGTH <value>关键字，仅保留长度≥value 的边缘片段；

  svrf

  // 仅报告长度≥0.1um的间距违规（过滤小凸起导致的虚假违规）
  met1_space_err = EXT MET1 < 0.3 MIN LENGTH 0.1

• 角度约束 ：使用ANGLE <range>关键字，仅测量特定角度范围内的边缘；

  svrf

  // 仅测量0°~10°或80°~90°的边缘（过滤倾斜边缘的虚假测量）
  met1_space_err = EXT MET1 < 0.3 ANGLE 0-10, 80-90

• 选择合适的度量标准 ：如Opposite度量避免拐角延伸导致的虚假测量。

六、summary

尺寸检查是 Calibre nmDRC 的核心功能，通过 EXTernal/INTernal/ENClosure 三大操作，结合度量标准、二级关键字和输出模式，可覆盖绝大多数 DRC 约束场景。使用时需重点关注：

1. 操作选型：根据约束类型选择合适的操作（间距→EXT，宽度→INT，包围→ENC）；
2. 度量标准：默认使用 Euclidean，特殊场景（拐角干扰 / 非对称测量）选用 Opposite/Square；
3. 约束与过滤：合理设置约束条件，使用MIN LENGTH/ANGLE抑制虚假测量；
4. 层级化适配：nmDRC-H 模式下避免隐性扁平化操作，优化性能。