数据在内存中的存储

1、整数在内存中的存储

1.1、大、小端字节序

就是数据在内存中的每个字节的存放的顺序；

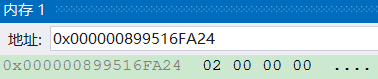
可以看到2本来内存中的存储是这样的 2是整型，32二个比特位，换算成16进制，应该是0x 00 00 00 02；为什么是这样的倒过来的？其实就是在存储设计上，设计了两种不同的存放方式；一个是大端字节序，一个是小端字节序；

比如0x 00 00 00 02，02部分就是低字节，在低位ie；0x 后面的部分 00 就是高字节；我们又知道在内存中它是又低地址到高地址存储的；

大端字节序就是，数据的低字节数据，存放到高地址，高字节数据，存放到低地址；也就是

00 00 00 02

小端字节序就是，数据的低字节数据，放到低地址，高字节数据，存放到高地址；也就是

02 00 00 00

为什么有这样呢？一个内存单元的大小就是一个字节，很多类型的大小是多个字节，那就会导致多个字节在内存中是如何排序的。

1.2、判断当前字节序

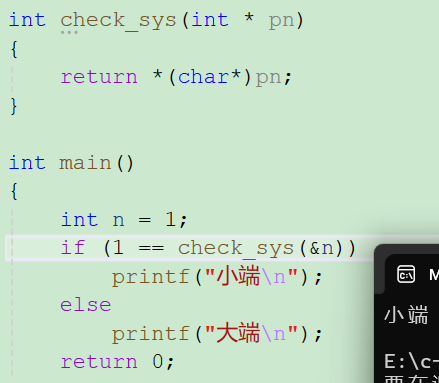
判断当前机器是大端字节序还是小端字节序其实不难；

比如1在内存中的存储，用16进制表示；假设是小端，就是01 00 00 00，如果是大端就是

00 00 00 01；那我们就比较第一个字节就可以了；如果是小端第一个字节就是1；大端就是0；

1.3、数据类型

做几个练习，感受一下；

首先我们要知道char的类型和它的取值范围；

我用的是vs2022;char是signed char，有符号的char；取值范围是-128~127；

取值范围是什么东西？比如char你能不能给一个超过这个范围的数，可以；500，10000都可以；但是char说你随便给，但是我认识这个范围里的数，我会把这些数转换为我认识的数；

比如下面的例子，我们先算-1在内存中的原码，再算出补码；但是char是8个字节的大小；发生截断；存了后8个字节；接着打印a；用%d打印；打印的是有符号的整数；所以要发生整型提升；但是我们要看a的类型；a是什么类型决定了它是如何整型提升的；a是有符号的整型；高位就用它的符号位补充；整型提升完后，它还是内存中的补码；打印的是原码；还得转为原码；

signed cha b 跟a是一样的都是有符号的char;

但是c是无符号的char；也是-1；发生截断；打印的是整数；发生整型提升；看c的类型；它是无符号的char；用0来补高位；它的原码反码补码相同；所以直接打印。

那类型的作用：

申请几个字节的内存空间
如何看待内存数据的视角比如c是无符号整型，那就是里面的数据，原反补相同

这个代码；一个1000个字符的数组；循环赋值；-1，-2，-3，-4.......，这里算它的长度；strlen是算到\0就会停止的。\0就是0；所以遇到0就是停止；但是这里会遇到0吗？

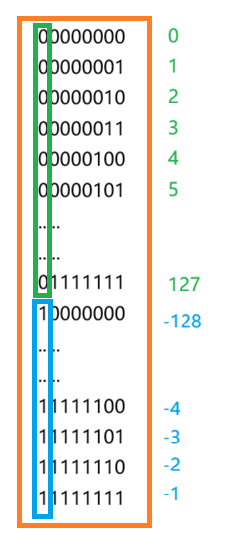
char的取值范围是-128~127；为什么是这个数，我们知道char的大小是8个字节；我们一直算算，从0开始算，一直算到11111111；但是char是一个有符号的char；那它的最高位是它的符号位；

那就是0，1，2，3，4；最高位就是1，就是负数；注意这些都是再内存中的补码；换成整数，从最底下开始就是-1，-2，-3，-4；一直到10000000，为什么10000000就是-128，你把-128换成32个比特位；取最后8个字节就是-128；如果是无符号的char就是没有符号位直接算；0，1，2...255;

就是这么来的；

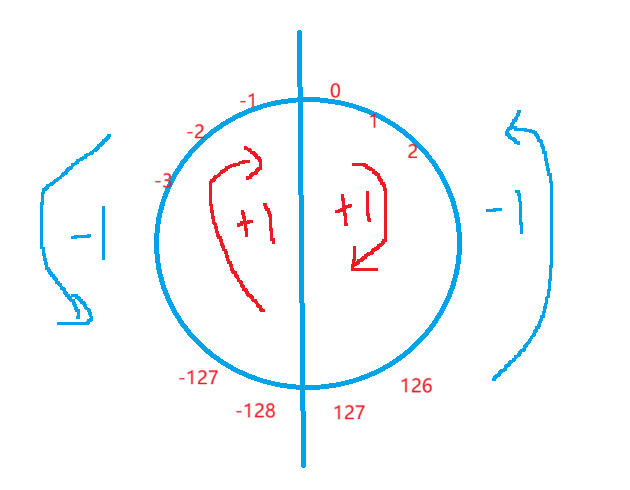
那我们发现在有符号的char算到127+1就变成了-128，算到-1+1，就是0了；我们可以画个图来理解，用个圆圈；右边从0开始，+1+1，到127；在+1就变成-128，一直+1，就变成-1了，再+1就变成0了；反过来-1也是一样的；这其实是一个轮回；

那我们会过来看代码；一直循环，a里面会有0吗？

循环赋值先从-1开始，-1，-2，-3....，-128，此时再-1，就是127，126，.....，0里；那-1到-128是127个字符，127到0是128个字符，相加就是128+127就是255个字符；

这个也是一样的，i 是无符号的char,取值范围是0~255；当i++；i=255为真，打印；打印完后上来++；这时候 i 就已经变成 0 ；死循环；

2、浮点数在内存中的存储

浮点数在内存中的存储跟整数是不一样的。

浮点数的存储是按照据国际标准IEEE（电⽓和电⼦⼯程协会）754，任意⼀个⼆进制浮点数V可以表⽰成下⾯的形式：

V = (-1)^S * M * 2^E
-1的S次方，表示符号位，S=0是整数，S=1是负数
M是有效数字，M是大于等于1，小于2
E是指数位

比如浮点数 9.5：

十进制是9.5
化成二进制是1001.1
9的二进制是1001，0.5的二进制就是1，因为小数点后面的权重是-1，-2....一直往后数
再把二进制化成科学计数法；也就是1.0011 * 2^3；因为是2进制，所以2^3。
再把它对应到这个公式；
因为是整数所以是 (-1)^0 * 1.0011 * 2^3
对应的就是S=0；M=1.0011；E=3
浮点数存储存的就是这个三个S 、M、E；存这三个就可以表示浮点数了。

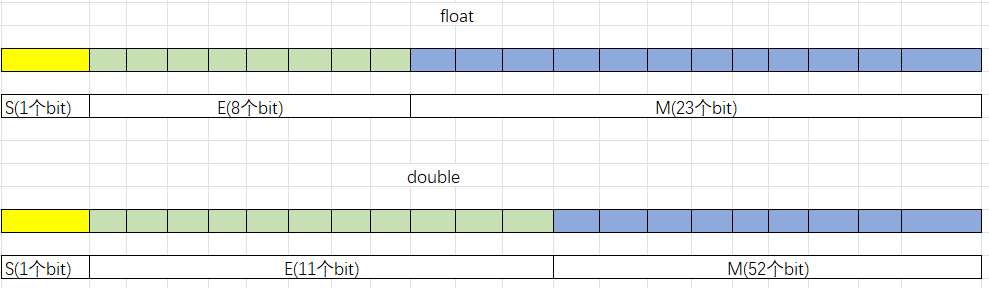
浮点数的存储是分类型的，float 和 double的类型是不一样的；每个数据的存储空间是不一样的；float是4个字节，32个bit;double是8个字节，64个bit。

2.1浮点数存储

S是符号位，放在最前面；负数就是1，正数就是0
M是有效数字，假如是float，给的是23个bit存储；存的是1.0011；前面的1.是不存进去的；因为每个浮点数转换成二进制的时候都是1<=M<2的，所以不存1. ，就存小数点后面的数字；整好多了一个位存有效数字；
E是一个无符号整数；当然有可能是负数，所以E存进去必须加上中间值；
float的要加上127；double的要加上1023

2.2浮点数取出来的过程

看E 是有1有0的情况：
就像9.5，E是3，存进去加上127；换成二进制是有1又有0的情况；那么就看S是不是正负数；再把M拿出来加上1. ，E取出来，2^E；就可以取出来了；
E是全1的情况：
假如是float；E存进去是要加上127；E是8个bit，全是1，就是255；谁加上127等与255；就是128；也就是原来的E是128；2^128，是一个很大的数字，就是无穷大；
E全是0
假如是float，E存进去是加上127；E全是0；那就是-127+127等于0；原本的E就是-127；就是2^127 / 1；是一个很小很小的数字；M取出来的时候就不会加上1 . ，就是直接0. ,表示很小的数

比如，下面的例子：

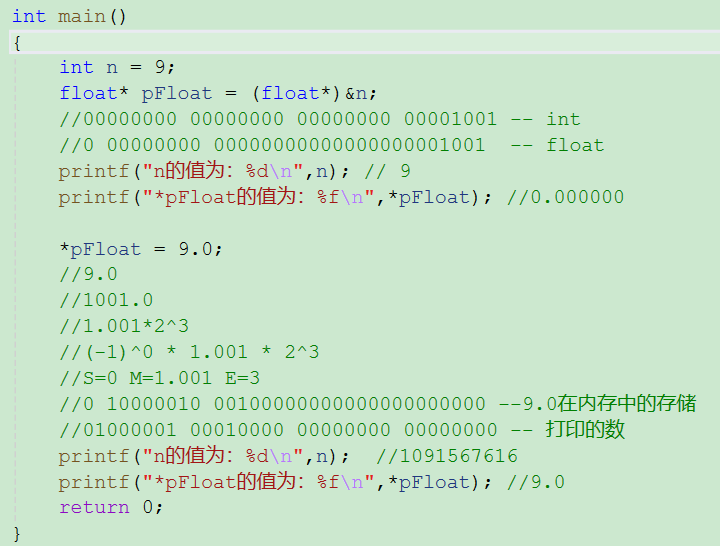
取n的地址强制类型转换float*；放到pFloat指针变量；

打印n的值；就是9；
第二个*pFloat的值；对pFloat解引用找的是n的地址，但是pFloat的类型是float；就是指向的对象是float；那就按照浮点数来取；先把9的在内存中存储的32个bit位，在按照float的S M E，那样来取；S取一个bit，接着E取8个bit；然后剩下的就是M；
第二个打印n的值；前面*pFloat就是n，存放了9.0；然后要打印；我们先看9.0它在内存是怎样存储的；再说要打印整数；再把原来数按照原来的整数格式打印；前面是符号位就是0；原码反码补码相同，直接打印；
最后一个，按照%f打印，没毛病

最后，为什么浮点数不能完全保留它的精度？

比如9.54；你把它换算成二进制，后面是0.5，比较好算，1001.1；小数点后面的权重是2^-1，2^-2，2^-3，2^-4，2^-5，一直下去，对应的就是0.5，0.25，0.125，0.0625.....以此类推；往后那几个位是1，加起来是0.04呢？，可能是1001.1000000000000000000001000000001；我们知道小数点后面的数存起来是23个bit位，如果是太大的数，是存不完；有些数更大，甚至超过了23个bit；那就是有些浮点数不能完全的保留其精度的；

比如我们判断浮点数是否相等，0.1+0.2 == 0.3，是不行的；

因为浮点数可能不会完全保留精度的，所以加起来未必等于0.3；

我们可以用另一种方法取判断浮点数是否相等；取两个浮点数的的绝对值，看是否小于给定的误差

用fabs函数，fabs函数用来取两个浮点数的绝对值；要头文件#include<math.h>

如果两个浮点数的绝对值小于给定的误差就视为相等；

感谢观看