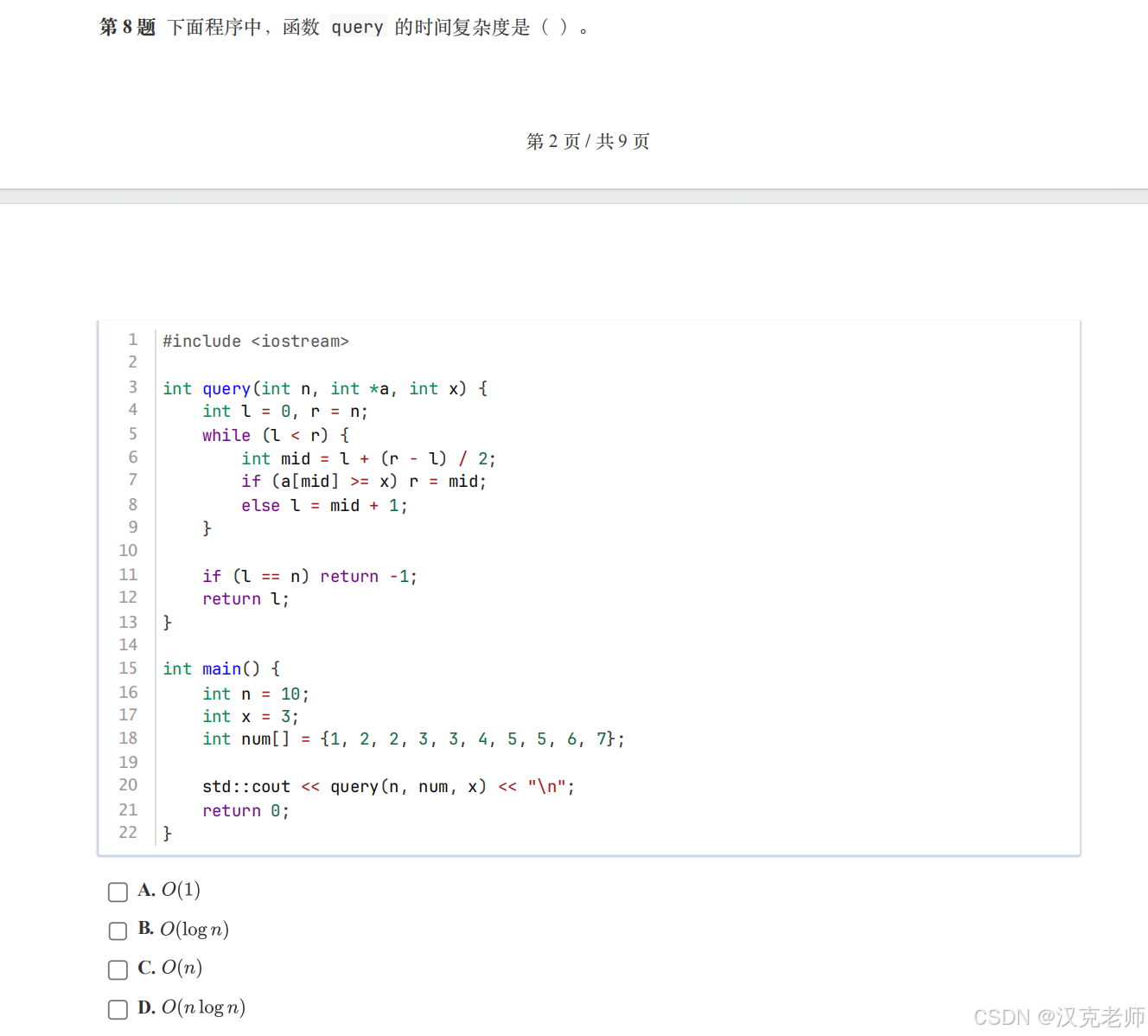
🧩 第 8 题:二分搜索小侦探(时间复杂度)
🎭 故事背景:找书的图书管理员
图书馆里有 10 本排好序的书:
cpp
int num[] = {1,2,2,3,3,4,5,5,6,7};管理员用一个聪明方法找数字 x = 3:
👉 不一本一本翻
👉 每次从中间切一半
🔍 这就是:二分查找(Binary Search)
cpp
while (l < r) {
int mid = (l + r) / 2;
...
}-
第一次:砍一半
-
第二次:再砍一半
-
第三次:再砍一半......
📉 每次都变成原来的一半
🧠 时间复杂度是多少?
如果有 n 本书:
cpp
n → n/2 → n/4 → n/8 → ...👉 要砍 log₂ n 次
✅ 正确答案:O(log n)
🎯 小学生记忆口诀
📚 排好队,砍一半
⏱️ 时间复杂度是 O(log n)

🧩 第 9 题:哈夫曼树的省力比赛(WPL)
🎭 故事背景:五个小精灵传话
5 个精灵说话次数是:
cpp
2, 2, 3, 3, 5规则:
-
说得越多 👉 路要越短
-
说得越少 👉 路可以长一点
👉 这就是 哈夫曼编码
🪜 建树规则(一步一步)
1️⃣ 找最小的两个:2 和 2 → 合并成 4
2️⃣ 再找最小:3 和 3 → 合并成 6
3️⃣ 再找最小:4 和 5 → 合并成 9
4️⃣ 最后:6 和 9 → 合并成 15
📐 计算 WPL(加权路径长度)
每一步合并的权值相加:
cpp
4 + 6 + 9 + 15 = 34✅ 正确答案:B(34)
🎯 记忆口诀
🐦 哈夫曼:小的先合,合并都要加
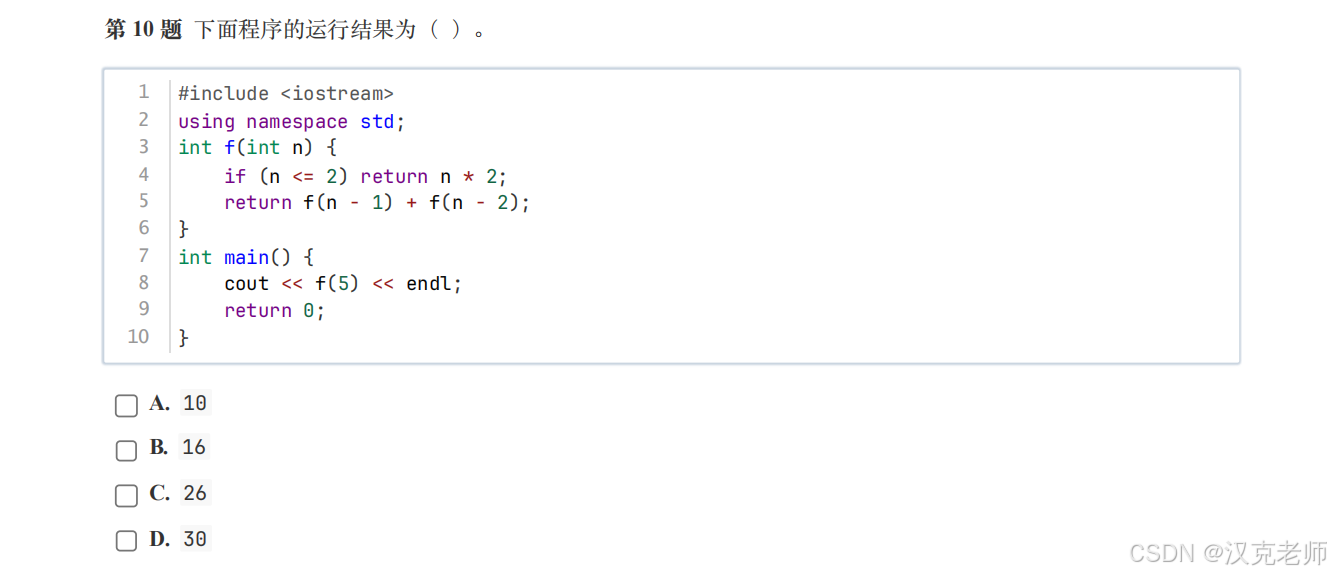
🧩 第 10 题:递归魔法球(函数调用)
cpp
int f(int n) {
if (n <= 2) return n * 2;
return f(n - 1) + f(n - 2);
}🧠 从最小开始算
cpp
f(1) = 2
f(2) = 4
f(3) = 6
f(4) = 10
f(5) = 16✅ 正确答案:B(16)
🎯 记忆口诀
🔁 递归不跳步
🪜 从底往上爬


🧩 第 11 题:图的握手定理
🎭 故事背景:数数有几人
-
图里有 36 条边
-
每个点都连着 4 条边
🧠 图论超级公式(一定要背)
所有点的度数之和 = 边数 × 2
计算:
cpp
36 × 2 = 72每个点 4 条边:
cpp
72 ÷ 4 = 18 个点✅ 正确答案:C(18)
🎯 记忆口诀
🤝 一条边,两个点
度数总和 = 边 × 2

🧩 第 12 题:二叉树真假话大会
1、正确答案:✅ D
在先序遍历中,根后面一定是左孩子
为什么?
🌳 先序遍历规则:
cpp
根 → 左 → 右所以:
-
第一个是根
-
第二个 一定来自左子树
-
左子树的第一个,就是左孩子
2、🧩 选项 A:中序遍历 ≠ 后序遍历,一定不一样?
❓ 选项 A 说了什么?
任意二叉树的中序遍历与后序遍历必定不相同
听起来好像很对?
但注意一个词:"任意" ❗
只要找到 一个反例,它就错了。
🎭 反例故事:只有一个结点的小树 🌱
cpp
A🧪 看三种遍历
-
先序:A
-
中序:A
-
后序:A
👉 中序 = 后序 = A
❌ 选项 A 被反例打败
🧠 小结
只要存在一种情况不成立
"任意" 这句话就错了
❌ 选项 A:错误
3、🧩 选项 B:先序 + 后序,一定能唯一确定二叉树?
❓ 选项 B 说了什么?
已知先序遍历和后序遍历,就能唯一确定二叉树
🎭 故事:两棵"长得不一样"的树
🌳 树 1(只有左孩子)
cpp
A
/
B🌳 树 2(只有右孩子)
cpp
A
\
B🧪 看遍历结果
树 1:
-
先序:A B
-
后序:B A
树 2:
-
先序:A B
-
后序:B A
👉 完全一样!
🤯 但树一样吗?
❌ 不一样!
🧠 小结
先序 + 后序
不一定能唯一确定二叉树
(除非题目说是"满二叉树",但这里没说)
❌ 选项 B:错误
4、🧩 选项 C:高度公式靠谱吗?
这一项考的是二叉树高度和结点数的关系 ,
但题目中的公式并不是二叉树的通用结论 ,
而是混淆了:
-
完全二叉树
-
满二叉树
-
普通二叉树
👉 条件不充分,结论却写死了
🧠 小结
高度和结点数之间
没有唯一固定公式(对所有二叉树)
❌ 选项 C:错误
5、🎯 记忆口诀
🌳 先序遍历:根一定最先,
根后面,一定先走左边!
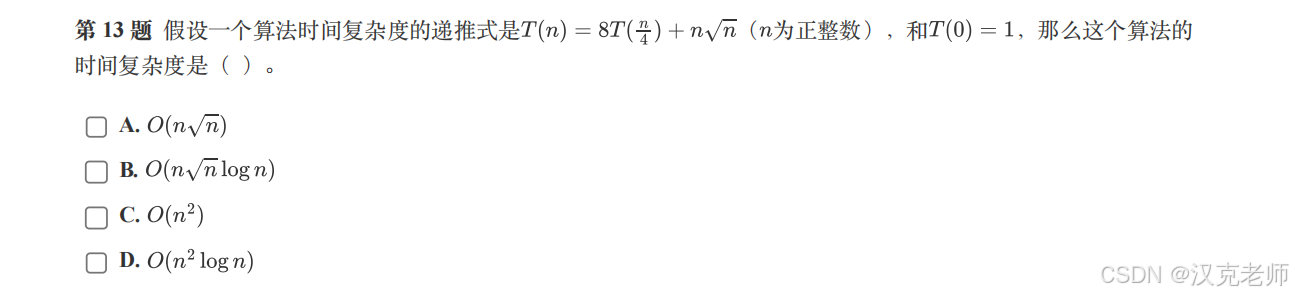
🧩 第 13 题:时间复杂度成长树
⏱️ 递推式的"分身怪兽"故事
📌 1、题目给的递推式
cpp
T(n) = 8T(n/4) + n√nn 是正整数
🧠 2、第一个关键问题(非常重要)
❓ 8T(n/4) 是什么意思?
它表示:
把一个大问题,分成 8 个子问题,
每个子问题的规模是 n/4
我们用一句"人话"翻译它:
原来有 n 个任务
老师说:
分成 8 组同学
每组只做 原来 1/4 那么多的任务
所以:
cpp
8T(n/4)
= T(n/4) + T(n/4) + ...(一共 8 次)🌳 3、这道题一定要用"递归树"来看
我们把算法想象成一棵树 🌳
🌱 第 1 层(最上面)
-
任务数:1 个
-
规模:n
-
本层额外工作量:
cpp
n√n🌿 第 2 层
-
子问题数:8 个
-
每个子问题规模:n/4
👉 每个子问题的额外工作量是:
cpp
(n/4)√(n/4)我们算一下(不怕,慢慢来)👇
🧮 4、关键计算(很多人卡在这里)
先拆 √(n/4)
cpp
√(n/4) = √n / 2所以每个子问题的工作量是:
cpp
(n/4) × (√n / 2)
= n√n / 8🌿 整个第 2 层的总工作量
这一层 有 8 个子问题:
cpp
8 × (n√n / 8) = n√n⚠️ 重要发现:
👉 第 2 层的总工作量 = 第 1 层 = n√n
🌲 5、第 3 层会怎样?
-
子问题数:8 × 8 = 64 个
-
每个规模:n / 16
你如果继续算,会发现一个神奇规律:
✨ 不管是哪一层,这一层的总工作量,永远是
n√n
⏱️ 6、一共有多少层?
每一层,规模都会变成原来的 1/4:
cpp
n → n/4 → n/16 → n/64 → ...直到变成 1 为止。
👉 问:要除以 4 几次,n 才会变成 1?
答案是:
cpp
log₄ n 层🧮 7、把所有层加起来(关键一步)
-
每一层的工作量:
n√n -
层数:
log n
所以:
cpp
总时间复杂度 = n√n × log n🏆 8、答案是 B
因为在选项中:
-
A:O(n√n) ❌(只算了一层,漏了 log)
-
B:O(n√n log n) ✅(每层一样 × 层数)
-
C:O(n²) ❌(太大了)
-
D:O(8ⁿ) ❌(指数爆炸,根本不是这种递归)
👉 所以答案是 B
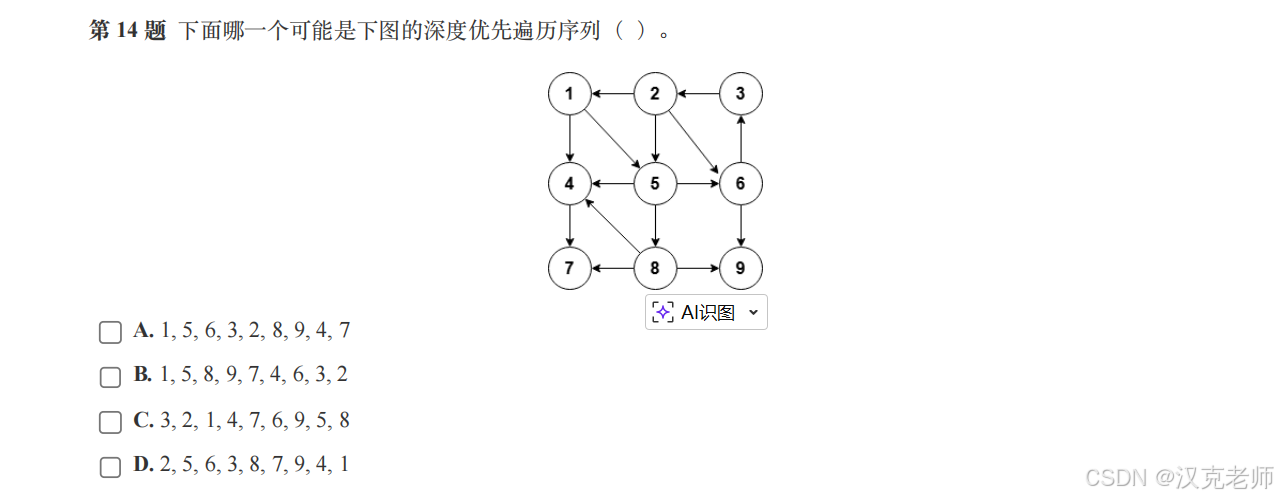
🧩 第 14 题:DFS 探险顺序
🎭 故事背景:迷宫探险
DFS 规则:
-
一条路走到黑
-
走不通再回头
正确答案:✅ B
👉 因为:
-
先深入
-
不会"来回跳"
其他选项都有 提前回头或乱跳
为什么其他选项不可能?
❌ A / C / D 的共同问题
它们都犯了一个 DFS 的大忌:
❌ 还没走到底,就突然"跳去别的分支"
举个例子(非常重要):
-
某个序列里:
-
你明明还能往下走
-
却突然回头 or 跳去另一个节点
-
👉 这在 DFS 中是 绝对不允许的
🎯 记忆口诀
🧭 DFS:不撞南墙不回头
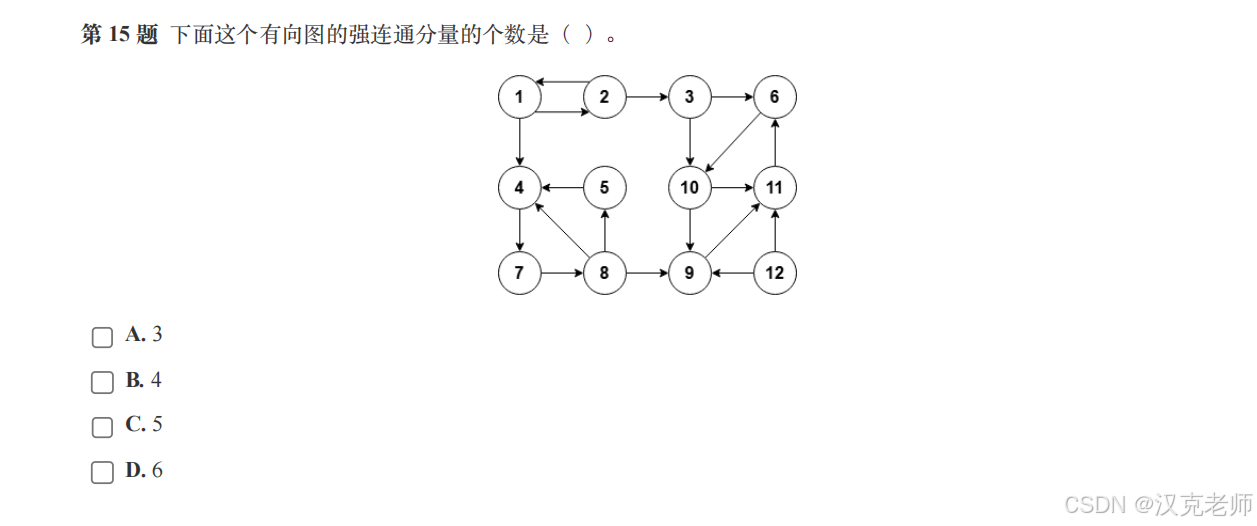
🧩 第 15 题:强连通分量
1、什么是"强连通分量"?(超重要)
🧒 定义
👯 一群点:
A 能走到 B
B 也能走回 A
👉 那它们就是一个 "小团体"
这个小团体就叫:
👉 强连通分量(SCC)
2、🎭 故事背景:我们来"分社团"
把整张图想象成 学生社团:
-
能互相来回串门的 = 一个社团
-
只能单向走、回不来的 = 不同社团
3、一步一步数"社团"(不跳步)
🟣 第 1 个社团
cpp
1 ↔ 2👉 互相能到达
✅ 一个 SCC
🟣 第 2 个社团
cpp
6 → 10 → 9 → 11 → 6
10 → 11👉 互相能到达
👉 形成一个闭环
✅ 一个 SCC
🟣 第 3 个社团
cpp
4 → 7 → 8 → 5 → 4
8 → 4👉 互相都能回来
✅ 一个 SCC
🟣 第 4/5 个社团
cpp
(单独的点,不能和其他互相回来) 3 , 12👉 自成一派
✅ 各自是一个 SCC
4、总数是多少?
我们数一数:
👉 一共 5 个强连通分量
正确答案:✅C
🎯 记忆口诀
🔁啥是强连通分量:
👉 "你能来我家,我也能回你家",
我们就在一个强联通分量里。