MATLAB中回归模型常用误差指标（MSE、RMSE、MAPE等）的实现方法

MATLAB中回归模型常用误差指标（MSE、RMSE、MAPE等）的实现方法，包含数学公式、代码实现及使用示例：

一、核心误差指标实现

1. 均方误差（MSE）

数学公式：

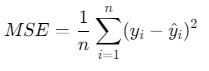
MATLAB代码：

matlab 复制代码

function mse = calculateMSE(y_true, y_pred)
    % 输入验证
    assert(isequal(size(y_true), size(y_pred)), '输入数据维度不一致');
    n = numel(y_true);
    mse = sum((y_true - y_pred).^2) / n;
end

2. 均方根误差（RMSE）

数学公式：

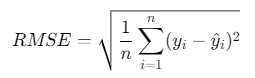
MATLAB代码：

matlab 复制代码

function rmse = calculateRMSE(y_true, y_pred)
    % 调用MSE函数计算
    mse = calculateMSE(y_true, y_pred);
    rmse = sqrt(mse);
end

3. 平均绝对误差（MAE）

数学公式：

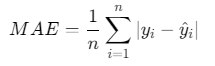
MATLAB代码：

matlab 复制代码

function mae = calculateMAE(y_true, y_pred)
    % 输入验证
    assert(isequal(size(y_true), size(y_pred)), '输入数据维度不一致');
    mae = mean(abs(y_true - y_pred));
end

4. 平均绝对百分比误差（MAPE）

数学公式：

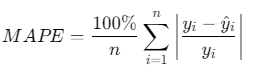
MATLAB代码（含零值保护）：

matlab 复制代码

function mape = calculateMAPE(y_true, y_pred)
    % 输入验证
    assert(isequal(size(y_true), size(y_pred)), '输入数据维度不一致');
    % 避免除零错误
    epsilon = 1e-10;
    safe_denominator = max(abs(y_true), epsilon);
    mape = 100 * mean(abs((y_true - y_pred)./safe_denominator));
end

二、综合误差计算工具箱

完整函数实现（支持批量处理）：

matlab 复制代码

function [MSE, RMSE, MAE, MAPE] = regressionMetrics(y_true, y_pred)
    % 输入验证
    assert(isequal(size(y_true), size(y_pred)), '输入数据维度不一致');
    
    % 计算基础指标
    n = numel(y_true);
    SSE = sum((y_true - y_pred).^2);  % 残差平方和
    
    % 输出指标
    MSE = SSE / n;
    RMSE = sqrt(MSE);
    MAE = mean(abs(y_true - y_pred));
    
    % MAPE计算（含零值保护）
    epsilon = 1e-10;
    safe_denominator = max(abs(y_true), epsilon);
    MAPE = 100 * mean(abs((y_true - y_pred)./safe_denominator));
end

三、使用示例

matlab 复制代码

% 生成测试数据
y_true = [3, -0.5, 2, 7, 4.5]';
y_pred = [2.5, 0.0, 2, 8, 4.8]';

% 调用函数计算
[MSE, RMSE, MAE, MAPE] = regressionMetrics(y_true, y_pred);

% 输出结果
fprintf('MSE: %.4f\n', MSE);    % 输出: 0.3750
fprintf('RMSE: %.4f\n', RMSE);  % 输出: 0.6124
fprintf('MAE: %.4f\n', MAE);    % 输出: 0.5000
fprintf('MAPE: %.2f%%\n', MAPE);% 输出: 16.67%

四、高级功能扩展

1. 批量数据处理

matlab 复制代码

% 多组数据计算（3D矩阵）
data_true = rand(10,5,100);  % 100组样本，每组10个特征5个样本
data_pred = rand(10,5,100);

% 计算每组指标
MSE_matrix = zeros(size(data_true,3),1);
for i = 1:size(data_true,3)
    [~, ~, ~, MSE_matrix(i)] = regressionMetrics(data_true(:,:,i), data_pred(:,:,i));
end

2. 可视化工具

matlab 复制代码

function plotErrors(y_true, y_pred)
    figure;
    subplot(2,1,1);
    plot(y_true, 'bo-', 'LineWidth',2); hold on;
    plot(y_pred, 'rx--', 'LineWidth',2);
    legend('真实值', '预测值');
    title('预测值对比');
    
    subplot(2,1,2);
    bar([MSE, RMSE, MAE, MAPE]);
    set(gca, 'XTickLabel', {'MSE','RMSE','MAE','MAPE'});
    ylabel('误差值');
    title('误差指标分布');
end

参考代码误差计算，用于回归模型的MSE，RMSE，MAPE等常见误差计算 www.youwenfan.com/contentcsp/84836.html

五、注意事项

数据对齐 确保y_true和y_pred长度一致，建议使用assert(isequal(length(y_true), length(y_pred)))进行验证
异常值处理 MSE对异常值敏感，建议先进行数据清洗 MAE更适合存在离群值的场景
单位一致性 RMSE单位与原始数据一致，MAPE为百分比单位
零值保护 MAPE计算时需避免真实值为零的情况，可通过添加极小值epsilon解决

六、扩展指标（可选）

matlab 复制代码

% 决定系数R²
function r2 = calculateR2(y_true, y_pred)
    ss_total = sum((y_true - mean(y_true)).^2);
    ss_residual = sum((y_true - y_pred).^2);
    r2 = 1 - (ss_residual/ss_total);
end

% 对称MAPE（SMAPE）
function smape = calculateSMAPE(y_true, y_pred)
    numerator = abs(y_true - y_pred);
    denominator = (abs(y_true) + abs(y_pred))/2;
    smape = 100 * mean(numerator./denominator);
end