光学学习笔记：详解光通量、照度、强度与亮度

在微纳光学（Micro-nano optics）和光学系统设计中，准确理解光的度量单位是建模的基础。

很多人分不清 Radiometry（辐射度学） 和 Photometry（光度学）。

• 辐射度学是纯物理的能量度量（客观，单位：瓦特 Watt）。
• 光度学是基于人眼感知的度量（主观，单位：流明 Lumen）。

本文将从数学定义的角度，彻底理清光度学四大金刚：光通量、光强、照度、亮度。

---

01. 全局概览图谱

在进入公式之前，先看这张经典的转换关系图。这是光学工程师必须印在脑子里的"地图"。

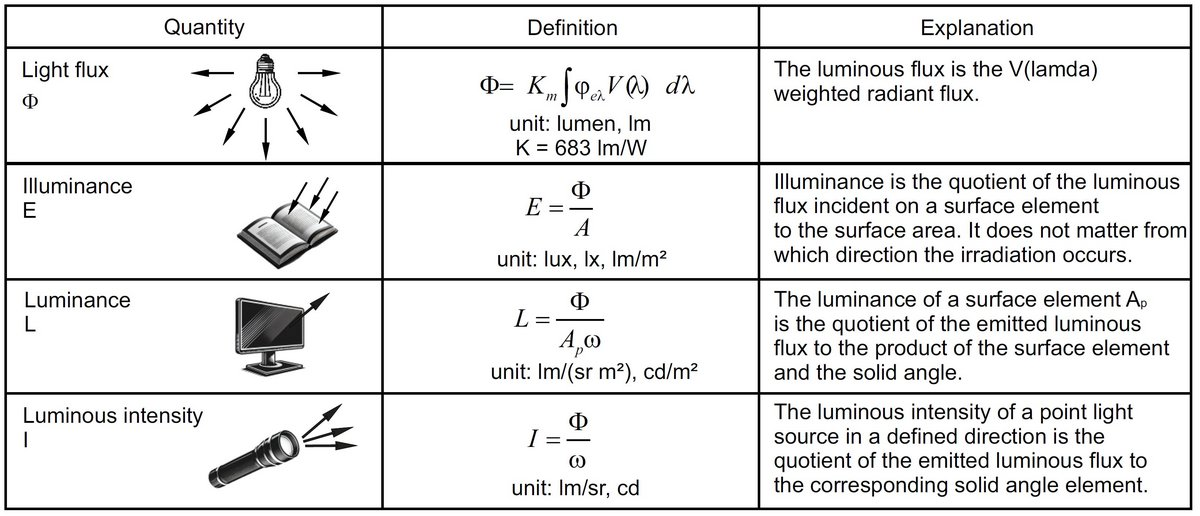
• 光源 (Source) 发出光通量 Φ\PhiΦ。
• 光在立体角 (Solid Angle) 内的密度是光强 III。
• 光打在接收面 (Surface) 上的密度是照度 EEE。
• 人眼 (Observer) 或是相机看到的发光面的明暗程度是亮度 LLL。

---

02. 深度拆解：四大物理量

1. 光通量 (Luminous Flux, Φv\Phi_vΦv)

定义 ：光源在单位时间内发出的光能量，根据人眼视见函数加权后的结果。

• 单位：流明 (Lumen, lm)
• 物理公式 ：
  hiv=Km∫380780P(λ)V(λ)dλ hi_v = K_m \int_{380}^{780} P(\lambda) V(\lambda) d\lambdahiv=Km∫380780P(λ)V(λ)dλ
  • P(λ)P(\lambda)P(λ)：光谱辐射功率分布 (Spectral Power Distribution)，单位 W/nmW/nmW/nm。
  • V(λ)V(\lambda)V(λ)：人眼视见函数（CIE 标准），在 555nm (绿光) 处达到峰值 1。
  • KmK_mKm：最大光视效能，约为 683 lm/W 。

  这意味着 1 Watt 的 555nm 绿光 ≈\approx≈ 683 lm ，而 1 Watt 的红外光 = 0 lm（因为人眼看不见）。

2. 发光强度 (Luminous Intensity, IvI_vIv)

定义 ：点光源在特定方向 上，单位立体角内发出的光通量。

• 单位：坎德拉 (Candela, cd)
• 物理公式 ：
  v=dΦvdΩ v = \frac{d\Phi_v}{d\Omega}v=dΩdΦv
  • Ω\OmegaΩ：立体角 (Solid Angle)，单位是球面度 (sr)。
  • 全空间的立体角是 4π4\pi4π sr。

  如果你把 LED 的发光角度压缩（加透镜），总流明 Φ\PhiΦ 不变，但立体角 Ω\OmegaΩ 变小，所以中心光强 III 会暴涨。这就是激光笔刺眼的原因。

3. 照度 (Illuminance, EvE_vEv)

定义 ：单位接收面积上接收到的光通量。它描述的是"被照面"的情况。

• 单位 ：勒克斯 (Lux, lx = lm/m2lm/m^2lm/m2)
• 物理公式 ：
  v=dΦvdA v = \frac{d\Phi_v}{dA} v=dAdΦv
• 距离平方反比定律 (Inverse Square Law) ：
  对于点光源，照度与距离的平方成反比：
  =Ir2⋅cos⁡θ = \frac{I}{r^2} \cdot \cos\theta=r2I⋅cosθ
  • rrr：光源到接收面的距离。
  • θ\thetaθ：光线入射角（光线与法线的夹角）。
  • 应用 ：在模拟探测器（Detector）上的能量分布时，如果你移动探测器使其距离加倍，照度理论上会变为原来的 1/4。

4. 亮度 (Luminance, LvL_vLv)

定义 ：发光面（或反射面）在单位投影面积 、单位立体角内发出的光通量。

• 单位 ：尼特 (nit = cd/m2cd/m^2cd/m2)
• 物理公式 ：
  v=d2ΦvdΩ⋅dA⋅cos⁡θ v = \frac{d^2\Phi_v}{d\Omega \cdot dA \cdot \cos\theta}v=dΩ⋅dA⋅cosθd2Φv
  • dA⋅cos⁡θdA \cdot \cos\thetadA⋅cosθ：这是投影面积 。当你侧着看屏幕时，投影面积变小了，所以需要除以 cos⁡θ\cos\thetacosθ 来修正。

  在理想光学系统（无损耗）中，光在传播过程中，亮度是不变的 。
  • 这就是为什么你不能通过透镜系统让成像比光源更"亮"（温度不能比光源更高）。

---

03. 辐射度学 vs 光度学：

做微纳光学仿真时，你通常输入的是 Laser Power (Watts)，但最后客户要看的是亮度 (Nits)。你需要这张对照表：

物理维度	辐射度学 (Radiometry) 能量/物理	光度学 (Photometry) 人眼/视觉	转换桥梁 (555nm)
能量/功率	辐射通量 Radiant Flux 单位: Watt (W)	光通量 Luminous Flux 单位: Lumen (lm)	1W=683lm1 W = 683 lm1W=683lm
空间强度	辐射强度 Radiant Intensity 单位: W/sr	发光强度 Luminous Intensity 单位: Candela (cd)	1W/sr=683cd1 W/sr = 683 cd1W/sr=683cd
接收面密度	辐照度 Irradiance 单位: W/m²	照度 Illuminance 单位: Lux (lx)	1W/m2=683lx1 W/m^2 = 683 lx1W/m2=683lx
源表面亮度	辐射亮度 Radiance 单位: W/(sr·m²)	亮度 Luminance 单位: Nit (cd/m²)	1W/(sr⋅m2)=683nit1 W/(sr\cdot m^2) = 683 nit1W/(sr⋅m2)=683nit

---

04. 典型计算案例

场景 ：

你有一个各向同性（各个方向发光均匀）的 LED 灯泡，总光通量为 1000 lm 。

你想知道：

1. 它的发光强度是多少？
2. 在距离它 2 米远的桌面上，照度是多少？

计算过程：

1. 求光强 (III)：

   • 因为是各向同性点光源，光向四面八方发射，立体角 Ω=4π≈12.57\Omega = 4\pi \approx 12.57Ω=4π≈12.57 sr。
   • I=ΦΩ=10004π≈79.6 cdI = \frac{\Phi}{\Omega} = \frac{1000}{4\pi} \approx \mathbf{79.6 \ cd}I=ΩΦ=4π1000≈79.6 cd。

2. 求照度 (EEE)：

   • 利用距离平方反比定律（假设垂直照射，cos⁡θ=1\cos\theta=1cosθ=1）：
   • E=Ir2=79.622=79.64≈19.9 lxE = \frac{I}{r^2} = \frac{79.6}{2^2} = \frac{79.6}{4} \approx \mathbf{19.9 \ lx}E=r2I=2279.6=479.6≈19.9 lx。

---

05. 总结

• Φ\PhiΦ (lm) 是源头的"总水量"。
• III (cd) 是喷头的"水压"。
• EEE (lx) 是地面的"湿润度"。
• LLL (nit) 是别人看过来觉得"刺不刺眼"。

做 Micro-nano optics 时，如果处理的是红外激光（如 1550nm），请直接忽略右边的光度学单位，死磕左边的 Radiometry (Watts) 即可，因为对于那样的波长，流明永远是 0。

---