一、二分类
事实证明,当实现神经网络时,有一些实现技巧会变得非常重要。例如,如果有一个包含M个训练样本的训练集,可能习惯于通过for循环逐步处理这M个训练样本,但通常希望在不使用显式for循环的情况下处理整个训练集
另外一个概念,当组织神经网络的计算时通常会有前向传播步骤,然后时反向传播步骤
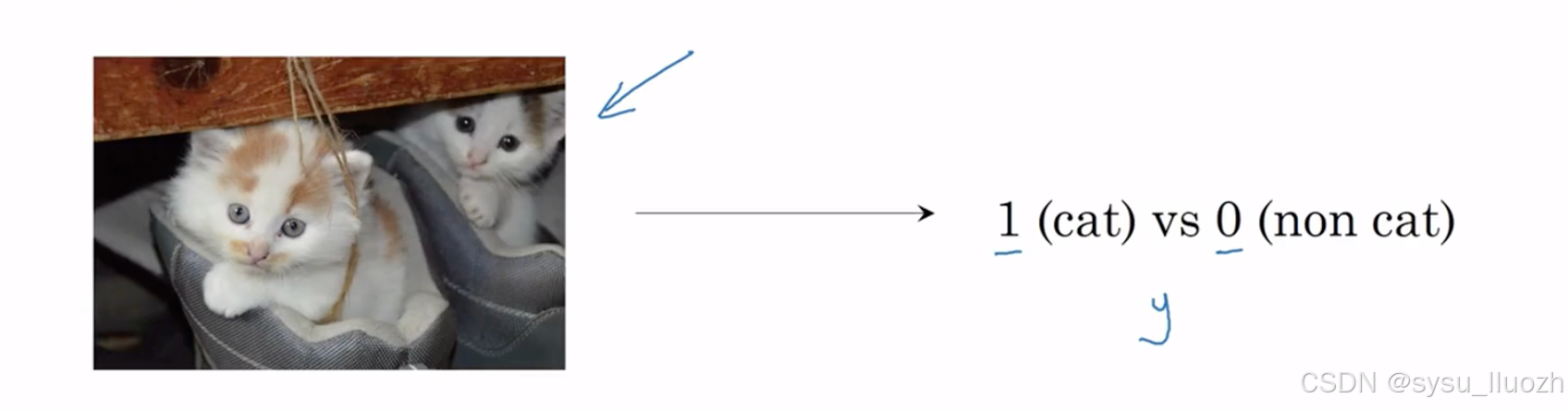
逻辑回归是一种二分类算法。这是一个二分类问题的例子,有一个像这样的图像输入,并希望输出一个标签来判断这是猫此时输出1,或者不是猫此时输出0。将用y表示输出标签
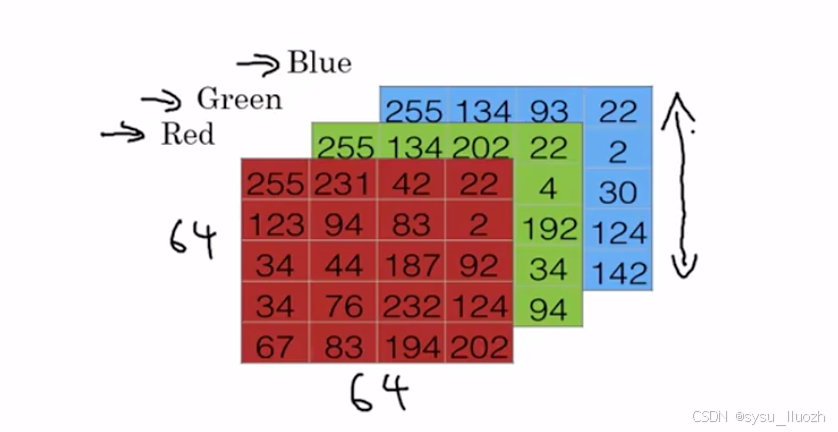
看看图像在计算机中的表示方式,要存储一张图像计算机会存储三个独立的矩阵分别对应红、绿、蓝三个颜色通道。如果输入图像是64 x 64像素,那么会有三个64 x 64的矩阵分别对应红、绿、蓝三个通道的像素强度值。现在画一个小得多的矩阵来表示,这些实际上是5 x 4的矩阵而非64 x 64
要将这些像素强度值转换为特征向量,需要展开所有这些像素值成为输入特征向量x。因此要将这些像素强度值展开为特征向量,需要定义一个特征向量x对应这张图像。将取出所有像素值255,231等等,直到列出所有红色像素,然后是255,134,直到得到一个很长的特征向量,列出所有红、绿、蓝通道的像素强度值
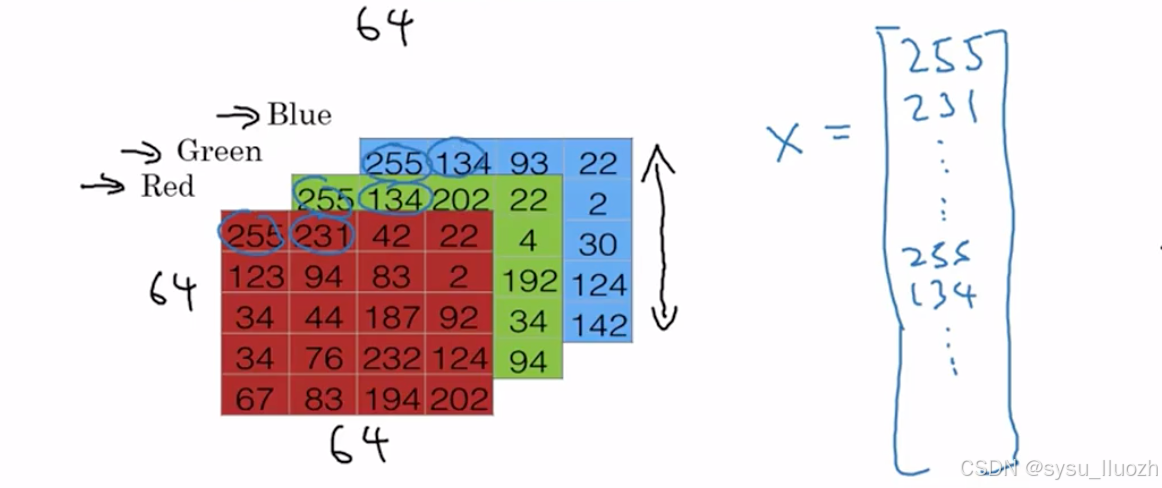
因此如果这是64 x 64的图像,这个向量x的总维度将是64 x 64 x 3,因为这是所有矩阵中数字的总数,在本例中结果是12288。因此将用nx = 12288来表示输入特征x的维度,有时为了简洁,也会用小写n来表示这个输入特征向量的维度
因此在二分类中,目标是学习一个分类器可以输入由特征向量x表示的图像,并预测对应的标签y是1还是0,即这是猫图像还是非猫图像
现在说明一些符号表示,后续会持续使用到。单个训练养呗由一对(x, y)表示,其中x是nx维特征向量,y是标签,取值为0或1
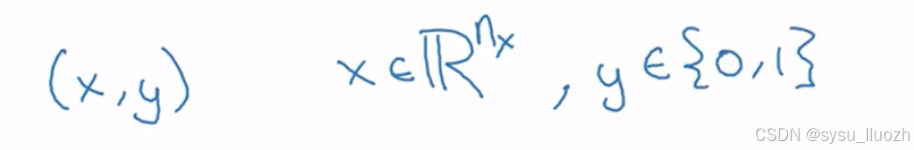
训练集将包含小写m个训练样本,因此训练集会记为(x1, y1),这是第一个训练样本的输入和输出,(x2, y2)对应第二个训练样本,直到(xm, ym),这是最后一个训练样本。这些共同构成了完整的训练集
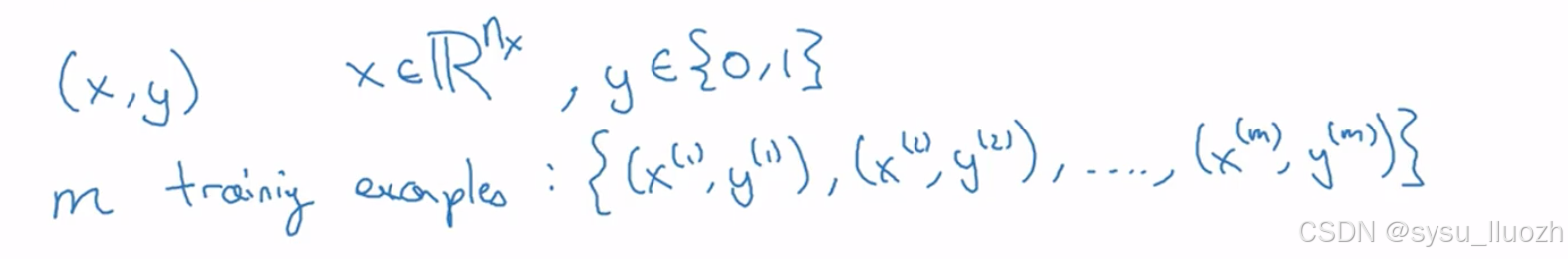
将用小写m表示训练样本数量,有时为了强调这是训练样本数量会写成m_train。当讨论测试集时,用m_test表示测试样本数量。为了用更紧凑的表示法组织所有训练样本,将定义一个矩阵X,其定义为取训练集x1,x2等输入,并按列堆叠。这个矩阵X将由m列,m是训练样本数量,而行数或者说矩阵高度是nx
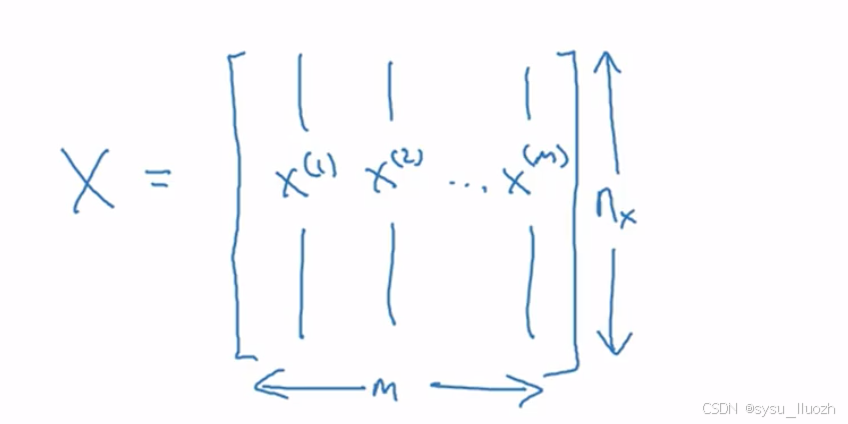
X是nx乘m维矩阵,在Python实现时,X · shape命令用于获取矩阵形状为(nx, m),这表示nx乘m维矩阵。这就是将训练样本输入X组织成矩阵的方法
那么输入标签Y呢?为了使神经网络实现更简单,将Y也按列堆叠。定义Y等于y1、y2直到ym,这里Y将是1 x m维矩阵。同样,用Python表示Y · shape为(1, m) ,即1 x m 矩阵
接下来有一个有用的约定是将与不同训练样本相关的数据(数据指X、Y或之后看到的其他量),将与不同训练样本相关的内容或数据按不同列堆叠,就像对X和Y的处理
二、逻辑回归
逻辑回归是一种学习算法,用于监督学习问题中输出标签y即非0即1的情况,也就是二分类问题
给定输入特征向量x,可能对应一张需要识别是否为猫图的图像,需要一个能输出预测值的算法,称之为y^(即对y的估计值)。更正式的说,希望y^表示在给定特征x时y等于1的概率
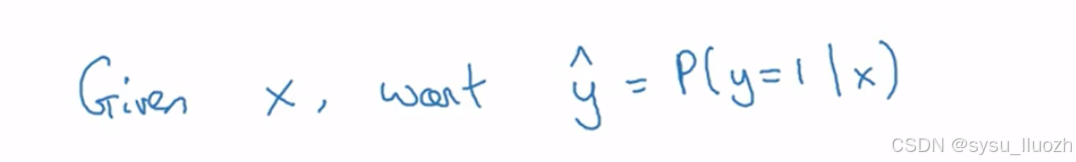
如果x是一张图片,希望y^ 能知道这是猫图的概率。如之前所说,x是一个x维向量,逻辑回归的参数将是w,它也是x维向量,以及b只是一个实数。给定输入x和参数w、b,如何生成输出y^呢?一个不可行的方式是让y^等于 w x + b,即x的线性函数
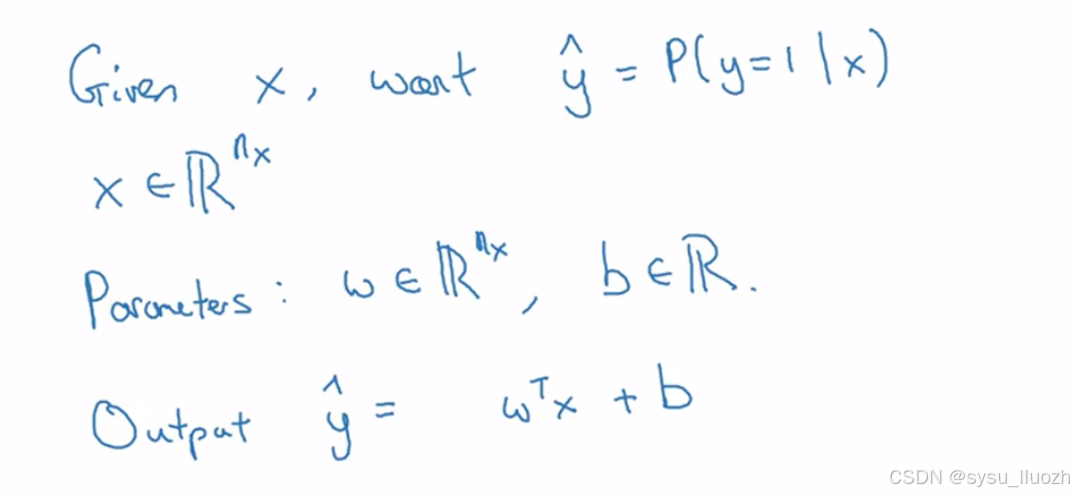
实际上,这正是线性回归的做法。但这不适用于二元分类,因为y^应是y=1的概率,所以y^应在0到1之间。而w x + b可能远大于1,甚至为负,这与概率应在0到1之前的要求矛盾。因此在逻辑回归中,输出改成y^等于这个量的sigmoid函数值
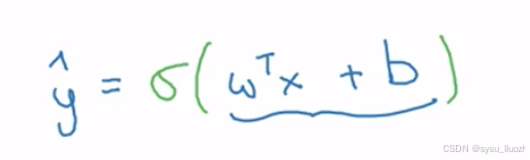
sigmoid函数函数图像如下
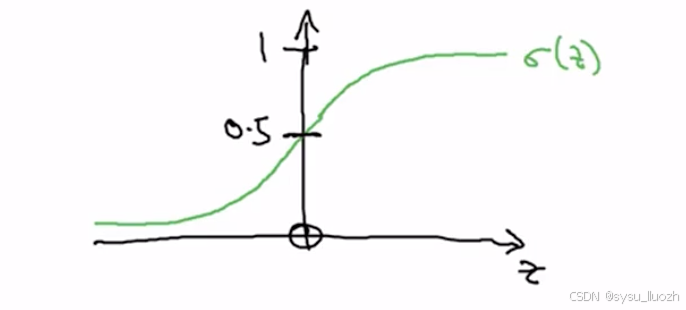
横轴表示z时,sigmoid(z)函数曲线如此,平滑地从0上升到1,曲线从纵轴0.5处穿过,这就是sigmoid(z)的图像
用z表示w x + b,sigmoid函数公式如下
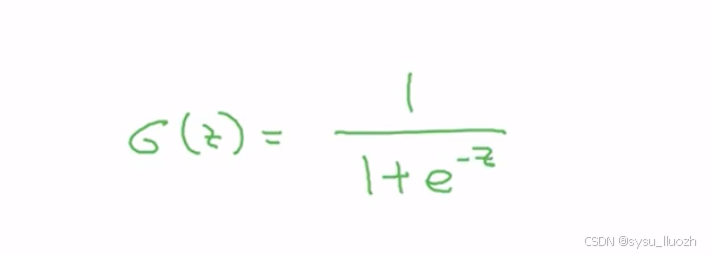
注意几点:
- 当z很大时,
e^(-z)接近0,因此sigmoid(z)约等于1 - 当z很小或是很大的负数时,
e^(-z)变为e的大数次方,可以看作1/(1+极大数),sigmoid(z)结果接近0
实现逻辑回归时,任务是学习参数w和b,使y^能准确估计y=1的概率。在编程神经网络时,通常分开处理参数w和b
三、回归逻辑的损失函数
要训练逻辑回归模型的参数w和b,需要定义一个成本函数,用于训练逻辑回归的成本函数。先看一下逻辑回归的输出函数
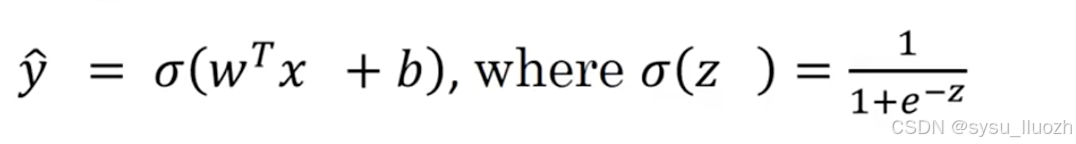
因此要学习模型参数,会获得包含m个训练样本的训练集,很自然希望找到参数w和b,预测值y^_i能够接近训练集中的真实标签y_i,即在训练集中获得的标签
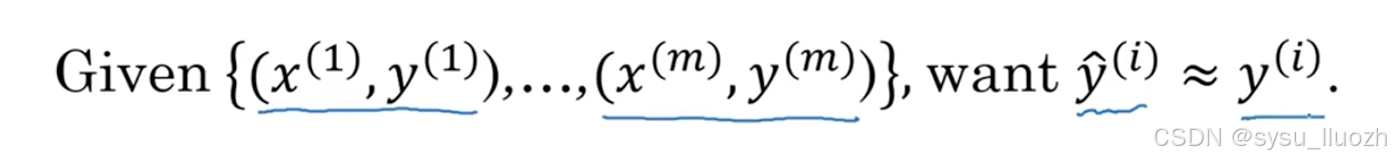
为了更详细说明顶部的方程,y^如顶部定义针对训练样本x,当然对于每个训练样本,使用()的上标来索引不同的训练样本。对第i个训练样本的预测,即y^_i将通过取Sigmoid函数获得,应用与w x_i,即该驯良样本的输入,加上b,可以如下定义z_i
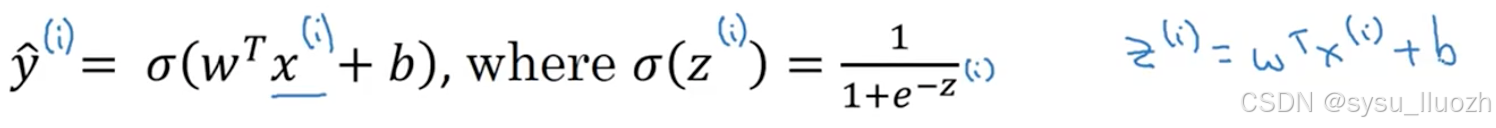
使用符号约定(i)表示数据,无论是x、y、z还是其他,与第i个训练样本相关联,这就是()的上标i的含义、
接下来看看使用什么损失函数或误差函数来衡量算法的表现。可以定义当算法输出y^而真实标签为y时的损失为平方误差或二分之一的平方误差
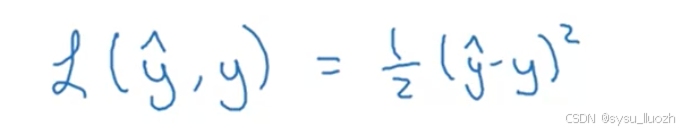
事实证明可以这样做,但在逻辑回归中通常不这样做,因为在学习参数时,会发现优化问题会变成非凸的,因此最终得到的优化问题会有多个局部最优解,因此提督下降可能找不到全局最优解
现在需要定义一个函数用于衡量当真实标签为y时输出y^有多好。平方误差看似是个合理选择,只是它会导致梯度下降效果不佳,因此在逻辑回归中,会定义一个不同的损失函数。它起到与平方误差类似的作用,但会给一个凸优化问题
因此,在逻辑回归中实际使用的损失函数如下
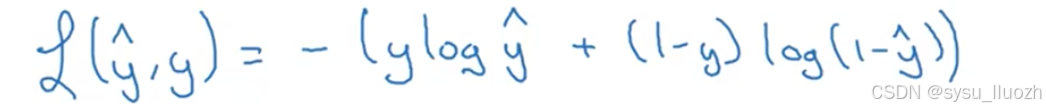
以下解释为何这个损失函数是合理的。请记住如果使用平方误差那么希望平方误差尽可能小,而对于这个逻辑回归损失函数同样也希望它尽可能小。为了理解其合理性,来看两种情况:
- 假设y = 1,那么损失函数仅等于
-ylog(y^),因为如果y等于1的话(1-y)log(1-y^)= 0,此时希望-ylog(y^)尽可能小,意味着log(y^)尽可能大,那么y^尽可能大,y^是Sigmoid(w x + b)永远不大于1,所以当y=1时,y^接近1 - 假设y = 0,那么损失函数仅等于
-(1-y)log(1-y^),因为如果y等于0的话ylog(y^)=0,此时希望-log(1-y^)尽可能小,意味着log(1-y^)尽可能大,因为y^必须在0和1之间,这意味着y^需要尽可能接近0
有很多函数具有大致相同的效果,即当y=1时,试图使y^变大,当y=0时,试图使y^变小