❤️本内容仅供本人阅读、学习,如有侵权,联系即删❤️
ARB-LLM:面向大型语言模型的交替精炼二值化方法
1 上海交通大学、2 苏黎世联邦理工学院、3 联想研究院
摘要
大型语言模型(LLMs)极大地推动了自然语言处理领域的发展,但它们高昂的内存和计算需求阻碍了实际部署。二值化作为一种有效的压缩技术,可将模型权重压缩至仅 1 位,显著降低对计算和内存的高需求。然而,现有二值化方法难以缩小二值化权重与全精度权重之间的分布差距,同时忽略了大型语言模型权重分布中的列偏差问题。为解决这些挑战,我们提出 ARB-LLM,一种专为大型语言模型设计的新型 1 位训练后量化(PTQ)技术。为缩小二值化与全精度权重的分布偏移,我们首先设计了交替精炼二值化(ARB)算法,通过逐步更新二值化参数,大幅降低量化误差。此外,考虑到校准数据的关键作用和大型语言模型权重的列偏差特性,我们进一步将 ARB 扩展为 ARB-X 和 ARB-RC。同时,我们通过列组位图(CGB)优化权重划分策略,进一步提升性能。为 ARB-X 和 ARB-RC 配备 CGB 后,我们分别得到 ARB-LLM_X 和 ARB-LLM_RC,它们在大型语言模型二值化任务中显著优于现有最先进(SOTA)方法。作为一种二进制训练后量化方法,我们的 ARB-LLM_RC 首次实现了超越同尺寸 FP16 模型的性能。相关代码和模型将在https://github.com/ZHITENGLI/ARB-LLM公开。
1 引言
近年来,基于 Transformer 架构(Vaswani,2017)的大型语言模型在各类自然语言处理任务中展现出令人瞩目的性能。然而,这种前所未有的能力在很大程度上归功于这些模型庞大的规模,它们通常包含数十亿个参数。例如,开源预训练 Transformer(OPT)系列(Zhang 等人,2022)涵盖多种模型,其中最大模型拥有 660 亿参数;类似地,LLaMA 系列模型(Touvron 等人,2023)包含 LLaMA-370B 等变体,架构规模更为庞大。此类大型模型推理时的内存需求极高(例如,700 亿参数模型需 150GB 内存),给其在移动设备上的部署带来了巨大挑战。
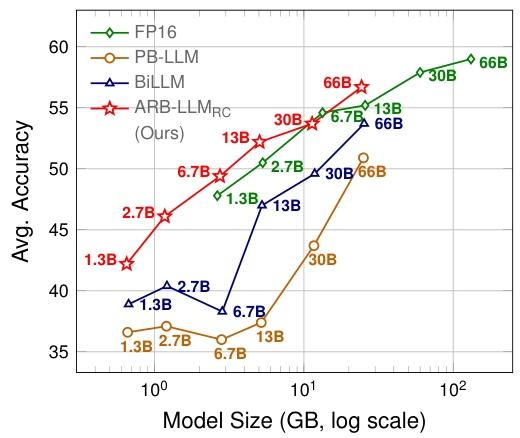
图 1:OPT 模型在 7 个零样本问答(QA)数据集上的性能表现。我们的 ARB-LLM_RC 模型优于同尺寸的 FP16 模型。
大型语言模型的压缩研究可分为权重量化(Lin 等人,2024;Frantar 等人,2023)、低秩分解(Zhang 等人,2024;Yuan 等人,2023)、网络剪枝(Sun 等人,2024;Frantar & Alistarh,2023)和知识蒸馏(Zhong 等人,2024;Gu 等人,2024)四类。其中,二值化作为量化领域的一种特定技术,因其能实现极致的内存压缩(将存储需求降至 1 位)而备受关注。考虑到大型语言模型的庞大尺寸,部分二值化方法采用训练后量化(PTQ)框架,可在极少资源消耗下快速将全精度模型转换为紧凑的二值化版本(例如,在单块 80GB GPU 上即可完成 700 亿参数模型的二值化)。
近期的二进制训练后量化方法(如 PB-LLM(Shang 等人,2024)和 BiLLM(Huang 等人,2024))强调对显著权重的识别,这些权重对模型性能至关重要(Lin 等人,2024)。通过对显著权重采用更高位表示和精细搜索策略,这些方法在性能与存储之间取得了较好的平衡。尽管取得了一定成功,但二值化过程本身的精炼问题仍未得到充分解决,导致二值化权重与全精度权重之间存在显著差异,这一差距成为进一步提升二进制大型语言模型性能的主要障碍。
为最大限度降低二值化过程中的量化误差,我们重新审视了二值化目标的求解方案。分析发现:(i)现有方法存在局限性,二值化后权重与全精度权重存在分布偏移,如图 2 所示,二值化权重的均值与全精度权重的均值未对齐。因此,基于二值化权重的初始分布精炼二值化参数,能更准确地估计原始权重;此外,这种精炼可交替应用于不同二值化参数,最终实现估计精度的显著提升。(ii)尽管校准集规模较小,但它在大型语言模型量化中起着关键作用;然而,将校准数据融入二值化参数更新(更贴合实际场景)的研究仍不够深入。(iii)大型语言模型的权重分布存在明显的列向偏差(见图 3),表明标准的行向二值化方法灵活性不足,可能并不适用。因此,结合行和列缩放因子能产生更具代表性的二值化结果。
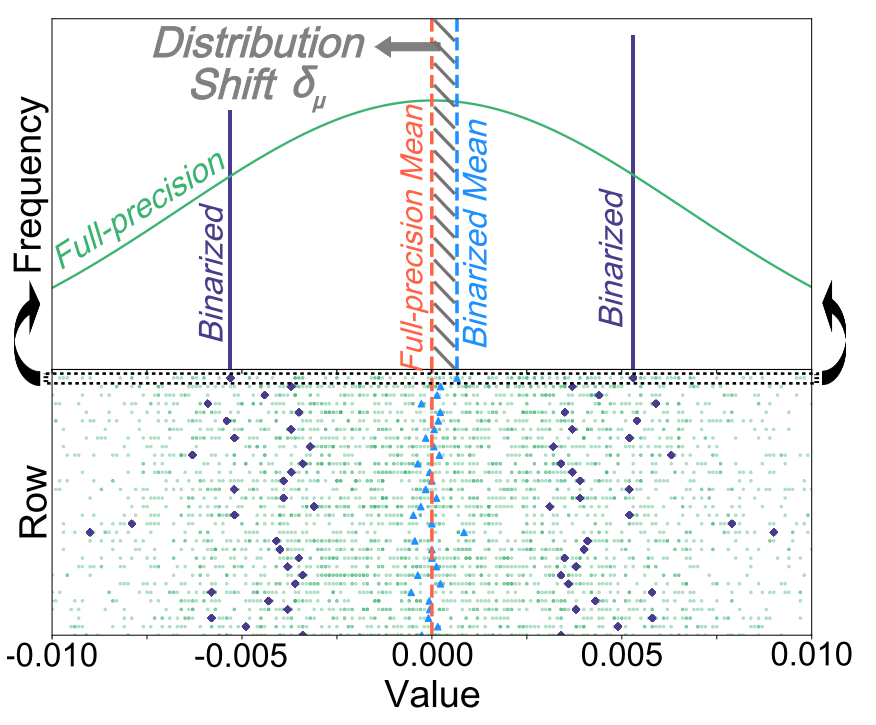
图 2:二值化权重与全精度权重的均值分布偏移。上图:单行的分布偏移;下图:多行的分布偏移。每行对应上图的俯视图。Distribution shift between the mean of binarized and full-precision weights. Top: distribution shift of one row. Bottom: distribution shifts of multiple rows. Each row represents a top view of the corresponding upper image.
基于上述观察与分析,我们首先提出交替精炼二值化(ARB)方法,以在标准二值化过程中对齐二值化与全精度权重的分布。随后,通过融入校准数据和行列双向缩放因子,将该方法扩展为两种高级变体:ARB-X 和 ARB-RC。此外,借鉴现有方法中区分显著与非显著权重、按幅度分组的思路,我们通过列组位图(CGB)优化了这两种划分方式的融合。
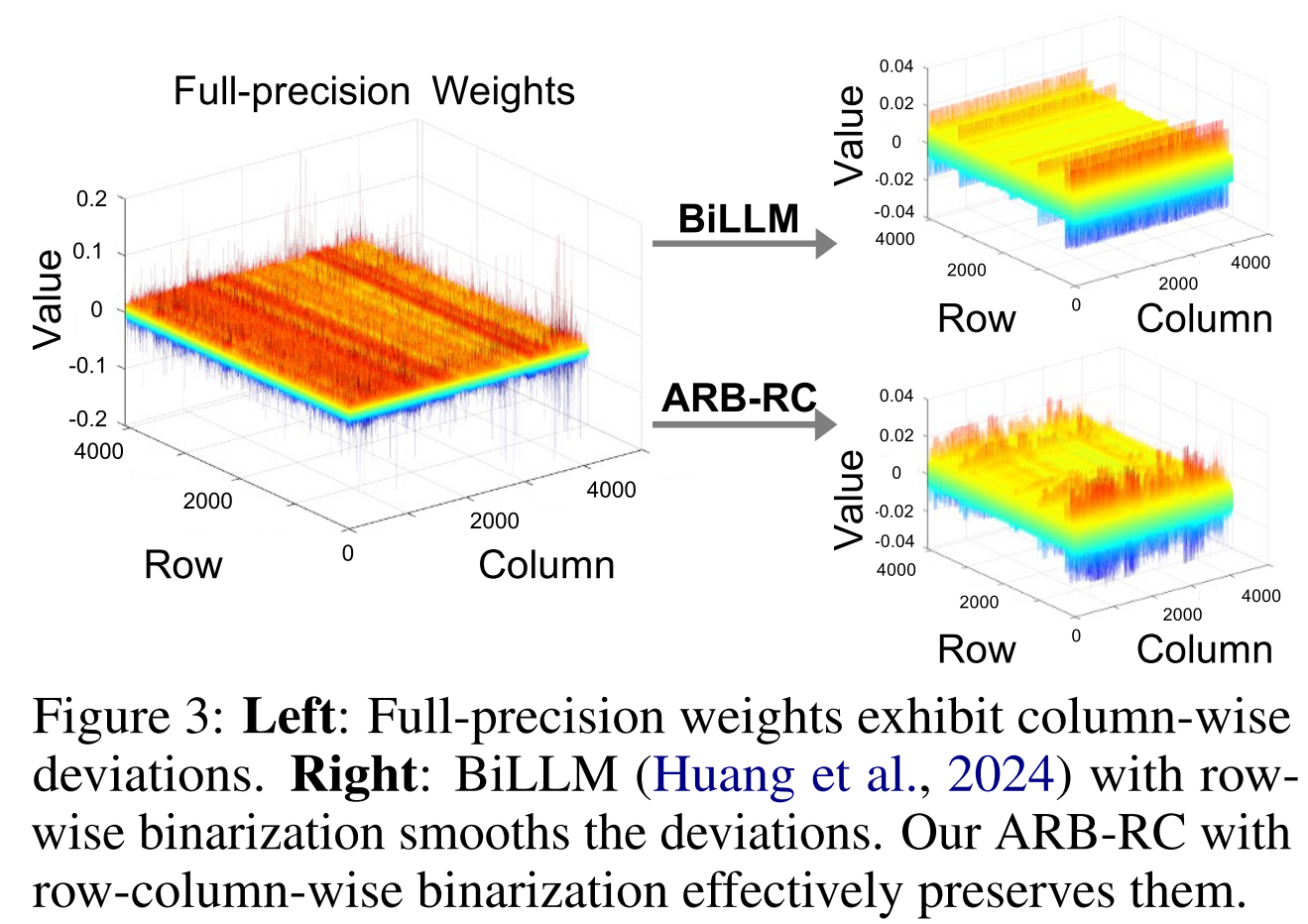
图 3:左图:全精度权重存在列向偏差;右图:采用行向二值化的 BiLLM(Huang 等人,2024)平滑了该偏差,而我们采用行列双向二值化 的 ARB-RC 模型有效保留了这一偏差特征。
本文的核心贡献如下:
- 提出新型二值化框架 ARB,通过逐步对齐二值化与全精度权重的分布 ,实现量化误差降低;同时,对逐步更新过程中的量化误差进行了严格的理论分析。
- 在基础 ARB 框架上,开发两种高级变体:融入校准数据的 ARB(ARB-X)和行列双向的 ARB(ARB-RC),分别针对二进制大型语言模型的特定挑战。
- 提出融合显著列位图与组位图的优化策略(CGB),提升位图利用率并进一步增强性能。
- 大量实验表明,我们的 ARB-LLM_RC(ARB-RC + CGB)在显著优于现有最先进二进制训练后量化方法的同时,所需内存更少;此外,ARB-LLM_RC 首次在零样本问答数据集上超越了同尺寸的 FP16 模型。
2 相关工作
2.1 网络二值化
网络二值化通过符号函数将参数压缩至仅 1 位(±1)。若训练二进制网络,需采用直通估计器(STE)(Bengio 等人,2013)解决反向传播过程中的梯度消失问题。二进制权重网络(BWN)(Rastegari 等人,2016)仅对权重进行二值化,保留全精度激活值;
XNORNet(Rastegari 等人,2016)进一步将权重和激活值均进行二值化,两者均聚焦于标准一阶二值化,并通过缩放因子 α 降低量化误差。网络草图(Guo 等人,2017)扩展了一阶二值化,提出二进制编码量化(BCQ),通过多个二进制矩阵逼近全精度权重;Xu 等人(2018)通过二叉搜索树确定最优编码,改进了 BCQ 方法,但这两种方法均适用于多轮二值化场景,无法应用于标准一阶二值化过程。
另一研究方向中,OneBit(Xu 等人,2024)将缩放因子扩展至权重和激活值;BinaryMoS(Jo 等人,2024)引入多个缩放专家提升性能,但这些模型的训练需要大量资源(例如,在 LLaMA-7B 上训练 OneBit 需使用 8 块 A100-80GB GPU,耗时 7 天)。
2.2 大型语言模型量化
当前大型语言模型的量化技术主要分为量化感知训练(QAT)和训练后量化(PTQ)框架。
量化感知训练(QAT)
QAT 将量化融入训练过程,使模型适应低比特表示。近期研究已成功将 QAT 应用于大型语言模型:LLM-QAT(Liu 等人,2024)通过无数据蒸馏解决了 QAT 训练中的数据壁垒问题;EfficientQAT(Chen 等人,2024)提出优化的两阶段 QAT 框架(Block-AP 和 E2E-QP),降低了大型语言模型 QAT 的内存和计算开销。然而,QAT 仍需大量计算资源,包括高额 GPU 内存和较长训练时间。因此,QLoRA(Dettmers 等人,2024a)等大型语言模型量化技术聚焦于参数高效微调方法,提升了 QAT 的效率,但大型语言模型量化方法的整体效率仍有待提升。
训练后量化(PTQ)
PTQ 直接对现有模型权重进行量化,无需重新训练,因此比 QAT 更快、更节省资源。近期研究已将 PTQ 有效应用于大型语言模型:RTN 通过将权重四舍五入至最近量化级别,确保大型语言模型量化后的高效运行;ZerqQuant(Yao 等人,2022)和 BRECQ(Li 等人,2021)通过为自定义量化块添加额外分组标签,提升了量化精度;GPTQ(Frantar 等人,2023)采用逐层量化策略,通过二阶误差补偿降低量化误差;此外,PB-LLM(Shang 等人,2024)、SpQR(Dettmers 等人,2024b)和 BiLLM(Huang 等人,2024)采用混合方法,对显著权重进行低比特量化,对非显著权重进行二值化;Smoothquant(Xiao 等人,2023)提出缩放权重和激活异常值的策略,简化了量化过程;此后,AWQ(Lin 等人,2024)和 OWQ(Lee 等人,2024)也提出对激活特征的显著权重进行尺度变换,以保留模型容量。本文工作属于二进制训练后量化范畴,相较于现有最先进方法 BiLLM 实现了显著性能提升。
3 方法
概述
如图 4 所示,为逐步对齐大型语言模型中二值化与全精度权重的分布,我们首先在 3.1 节提出交替精炼二值化(ARB)框架。基于该框架,3.2 节提出融入校准数据的交替精炼二值化(ARB-X),以提升校准集的利用率(校准集对二进制大型语言模型至关重要);3.3 节提出行列双向交替精炼二值化(ARB-RC),以解决大型语言模型权重的列偏差问题;3.4 节讨论融合显著列位图与组位图的优化策略(CGB)。最终模型 ARB-LLM_X 和 ARB-LLM_RC 分别通过为 ARB-X 和 ARB-RC 配备 CGB 得到。
3.1 交替精炼二值化(ARB)
首先讨论大型语言模型中的标准权重二值化。对于全精度权重\( W \in \mathbb{R}^{n ×m} \),二值化目标定义为(为简化省略维度广播):
\( \underset{\alpha, B}{arg min }\| \tilde{W}-\alpha B\| {F}^{2} \),其中\( \tilde{W}=W-\mu \),\( \mu=\frac{1}{m} \sum{j=1}^{m} W_{. j} \)
其中,\( \alpha \in \mathbb{R}^{n} \)表示行缩放因子,\( B \in \{+1,-1\}^{n ×m} \)为二进制矩阵。
由于权重的均值不一定为零,通常在二值化前进行行向重分布,使权重达到行向零均值分布,以简化二值化过程。在上述二值化目标下(公式(1)),α和B的最优解可求解为\( \alpha=\frac{1}{m} \sum_{j=1}^{m}|\tilde{W}{. j}| \)和\( B=sign(\tilde{W}) \)。二值化后的量化误差\( \mathcal{L}{1} \)定义为:
\( \mathcal{L}_{1}=\| W-\hat{W}\| _{F}^{2} \),其中\( \hat{W}=\alpha B+\mu \) (2)
接下来,我们旨在研究如何降低量化误差\( \mathcal{L}{1} \)。首先定义残差矩阵\( R=W-\widehat{W} \),分析发现残差矩阵R存在分布偏移------由于二值化过程中不可避免的误差,R的均值并不总是零(见图2)。为解决这一问题,我们为原始均值μ引入修正项\( \delta{\mu} \),有效缓解分布偏移,精炼均值定义如下:
\( \mu_{refine }=\mu+\delta_{\mu} \),其中\( \delta_{\mu}=\frac{1}{m} \sum_{j=1}^{m} R_{. j} \) (3)
这等价于对\( \mathcal{L}{1} \)求关于μ的偏导数并令其等于0,如图4所示。由于μ已更新为\( \mu{refine } \),原始的α和B不再是量化误差\( \mathcal{L}{1} \)的最优解。为进一步最小化量化误差,令\( \partial \mathcal{L}{1} / \partial \alpha=0 \),可得到\( \alpha_{refine } \)和\( B_{refine } \)的最优解:
\( \alpha_{refine }=\frac{1}{m} diag\left(B^{\top}\left(W-\mu_{refine }\right)\right) \),\( B_{refine }=sign\left(W-\mu_{refine }\right) \) (4)
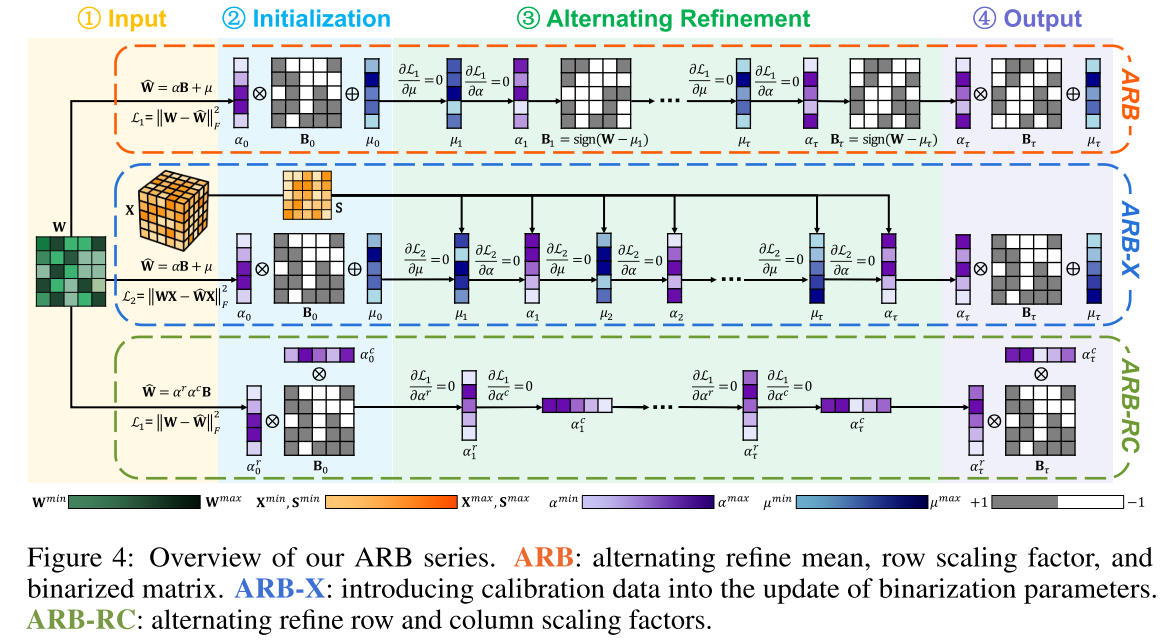
图4:ARB系列方法概述。ARB:交替精炼均值、行缩放因子和二值化矩阵;ARB-X:将校准数据引入二值化参数更新过程;ARB-RC:交替精炼行缩放因子和列缩放因子。
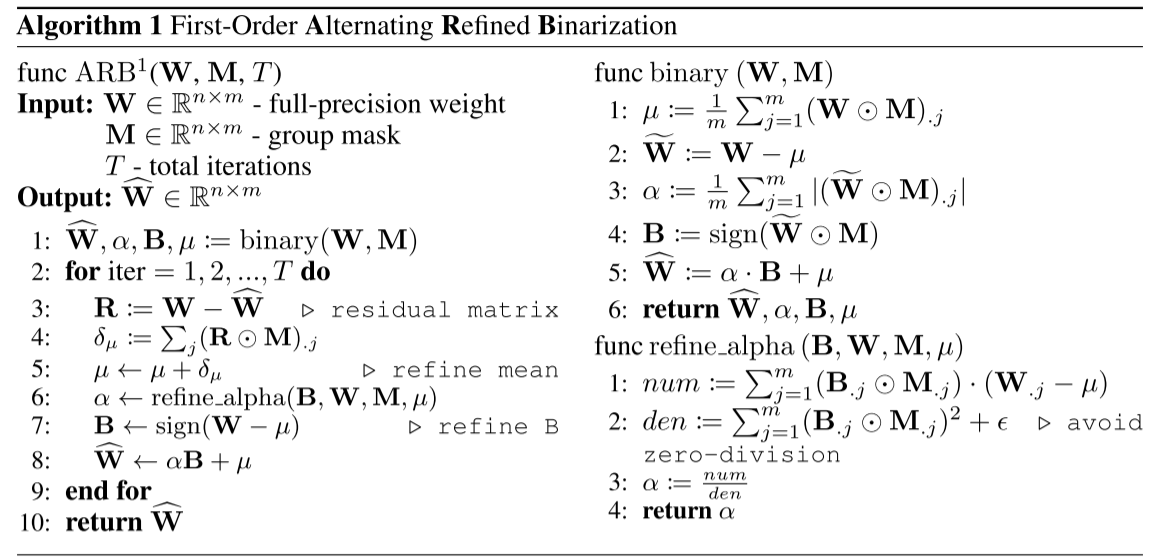
精炼μ、α和B后,可得到\( \widehat{W}{refine }=\alpha{refine } \cdot B_{refine }+\mu_{refine } \)。我们发现该参数更新策略可扩展为迭代算法:在每次迭代中,依次更新μ、α和B,确保它们在当前量化误差\( \mathcal{L}_{1} \)下为最优解。伪代码见算法1(该算法通过组掩码扩展了ARB,组掩码为3.4节详细介绍的位图)。此外,我们对ARB过程中的量化误差进行了理论分析,推导得到T次迭代后量化误差的降低值(见定理1),证明过程见补充文件。

3.2 融入校准数据的交替精炼二值化(ARB-X)
校准集虽规模小,但对大型语言模型量化至关重要。为充分利用校准数据,我们将其融入二值化参数更新过程,提出 ARB-X。
误差重构
标准量化误差\( \mathcal{L}{1} \)仅考虑权重本身,未反映模型在真实数据上的性能。因此,我们引入校准数据X,将误差定义为模型输出误差:
\( \mathcal{L}{2}=\| W X-\hat{W} X\| {F}^{2} \) (8)
其中,\( \hat{W}=\alpha B+\mu \)为二值化权重。直接计算\( \mathcal{L}{2} \)的时间复杂度较高,我们对其进行重构以提升效率。展开公式(8)可得:
\( \mathcal{L}{2}=\left\| (W-\mu-\alpha B) X \right\| {F}^{2}=Tr\left( X X^{\top} (W-\mu-\alpha B)^{\top} (W-\mu-\alpha B) \right) \)
令\( S=\sum{b} X{b}^{T} X_{b} \)(X_b为校准数据的分块),则:
\( \mathcal{L}{2}=\left<S, R^{\top} R\right>{F}=Tr\left(R S R^{\top}\right) \),其中\( R=W-\mu-\alpha B \) (9)
为衡量重构后的效率提升,我们定义加速比η(原始误差计算与重构后方法的时间复杂度之比),理论结果见定理2,证明过程见补充文件。
定理2:重构方法相较于原始方法的加速比η为:
\( \eta \propto \frac{1}{k \cdot\left(\frac{1}{n \cdot T}+\frac{1}{B \cdot L}\right)} \)
其中,n为权重的隐藏维度,k为块大小,T为迭代次数。

通常,我们设置n=4096、B=128、L=2048、T=15、k=128,此时η约为389,即重构方法比原始方法快约389倍,详细信息见补充文件。
参数更新
结合参数更新策略与重构后的\( \mathcal{L}{2} \),令\( \partial \mathcal{L}{2} / \partial \mu=0 \)和\( \partial \mathcal{L}_{2} / \partial \alpha=0 \),可推导得到ARB-X的参数更新公式,依次更新μ和α:
\( \mu=\frac{1^{\top} S(W-\alpha B)^{\top}}{1^{\top} S 1} \),\( \alpha=\frac{diag\left(B S(W-\mu)^{\top}\right)}{diag\left(B S B^{\top}\right)} \)
需注意,此过程中不更新矩阵B------由于B由离散值(+1和-1)组成,无法通过令\( \mathcal{L}_{2} \)对B的偏导数为零直接更新。一阶和二阶ARB-X的伪代码见补充文件。
3.3 行列双向交替精炼二值化(ARB-RC)
现有二值化方法采用行向缩放因子\( \alpha^{r} \)进行权重二值化,但我们对大型语言模型权重矩阵W的数值分布分析发现,列间存在显著偏差(部分列的值明显更大,见图3)。因此,单一的行向缩放因子可能无法有效捕捉大型语言模型参数的分布特征;此外,权重分布的均值接近零,使得行向零均值重分布在大型语言模型二值化中效果有限。
为解决这一问题,我们提出ARB-RC算法:引入列向缩放因子\( \alpha^{c} \)以更好地处理列间参数差异,同时去除重分布参数μ以增强大型语言模型的压缩效果。行列双向二值化过程如下:
\( \alpha^{r}=\frac{1}{m} \sum_{j=1}^{m}\left|W_{. j}\right| \),\( \alpha^{c}=\frac{1}{n} \sum_{j=1}^{n}\left|\frac{W_{j .}}{\alpha_{j}^{r}}\right| \),\( B=sign(W) \)
二值化矩阵为\( \widehat{W}=\alpha^{r} \alpha^{c} B \)------去除μ并引入\( \alpha^{c} \)在减少参数的同时提升了模型性能。然而,仅引入\( \alpha^{c} \)而不采用交替参数更新策略,不仅无法提升性能,反而可能增加量化误差。因此,需将\( \alpha^{c} \)与ARB算法结合,基于量化误差\( \mathcal{L}{1} \)优化参数。尽管量化误差\( \mathcal{L}{2} \)更贴合实际场景,但分析表明,在ARB-RC中融入X会导致参数耦合,增加优化难度(详见补充文件)。因此,基于\( \mathcal{L}{1} \),令\( \partial \mathcal{L}{1} / \partial \alpha^{r}=0 \)和\( \partial \mathcal{L}_{1} / \partial \alpha^{c}=0 \),分别更新\( \alpha^{r} \)和\( \alpha^{c} \):
\( \alpha^{r}=\frac{diag\left(W\left(\alpha^{c} B\right)^{\top}\right)}{diag\left(\left(\alpha^{c} B\right)\left(\alpha^{c} B\right)^{\top}\right)} \),\( \alpha^{c}=\frac{diag\left(W^{\top}\left(\alpha^{r} B\right)\right)}{diag\left(\left(\alpha^{r} B\right)^{\top}\left(\alpha^{r} B\right)\right)} \)
ARB-RC的一阶和二阶伪代码见补充文件。
3.4 列组位图(CGB)
受BiLLM(Huang等人,2024)启发,我们将所有权重划分为显著列和非显著列,并对显著权重采用更高比特表示(即二阶二值化)。与BiLLM不同的是,我们不仅将非显著权重分为稀疏组和密集组,还对显著权重进行类似分组,该方法可更高效地利用列位图和组位图(见图5)。
为识别权重的敏感性(即显著权重),我们采用成熟的PTQ方法,以Hessian矩阵为标准判据,敏感性计算为\( s_{i}=w_{i}^{2} /[H^{-1}]_{i i}^{2} \),其中H为每层的Hessian矩阵,\( w_i \)为每个列的原始值。选择敏感性较高的列作为显著列,详细内容见Huang等人(2024)。
4 实验结果
4.1 实验设置
模型与数据集
我们在多个开源大型语言模型家族上进行实验,包括 OPT(Zhang 等人,2022)、LLaMA1&2&3(Touvron 等人,2023)和 Vicuna(Chiang 等人,2023),模型尺寸涵盖 1.3B 至 70B。实验任务包括零样本问答(QA)和语言建模(困惑度):零样本问答任务采用 7 个数据集(ARC、BoolQ、Hellaswag、PIQA、Winogrande、OpenBookQA、RACE),语言建模任务采用 WikiText2 和 C4 数据集。
对比方法
我们与以下最先进方法进行对比:
- 训练后量化(PTQ ):RTN(四舍五入量化)、GPTQ (Frantar 等人,2023)、PB-LLM (Shang 等人,2024)、BiLLM(Huang 等人,2024);
- 全精度模型:FP16(16 位浮点模型)。
所有对比方法均采用官方实现和推荐超参数,我们的方法基于 PyTorch 框架实现,详细超参数见补充文件。
4.2 主要结果
零样本问答性能
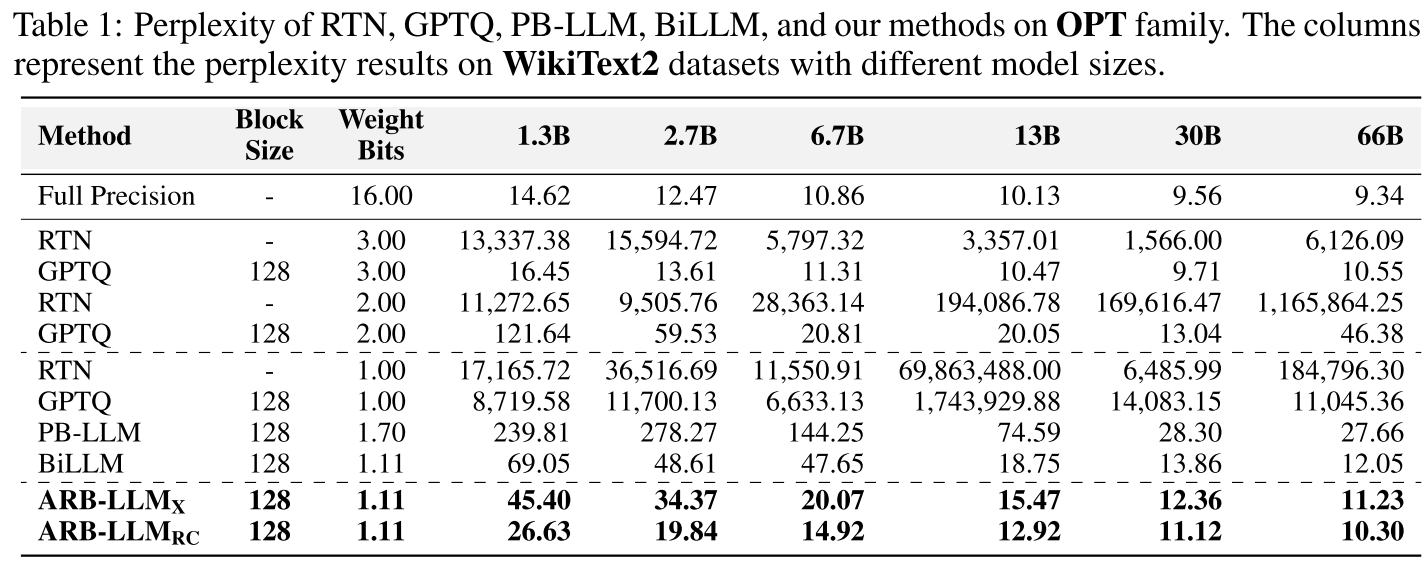
图 1 展示了 OPT 模型在 7 个零样本问答数据集上的平均准确率。可以看出,我们的 ARB-LLM_RC 在所有模型尺寸下均显著优于现有最先进二进制 PTQ 方法(PB-LLM、BiLLM),且首次实现了超越同尺寸 FP16 模型的性能。例如,OPT-66B 模型中,ARB-LLM_RC 的平均准确率比 FP16 高约 2%,比 BiLLM 高约 5%。
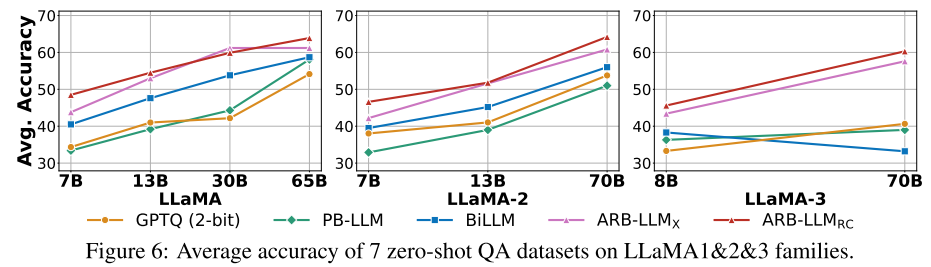
图 6 展示了 LLaMA1&2&3 系列模型在零样本问答任务上的平均准确率。结果表明,ARB-LLM_X 和 ARB-LLM_RC 均大幅优于 BiLLM,且 ARB-LLM_RC 的性能最为突出。此外,ARB-LLM_RC 在部分模型上(如 LLaMA-70B)甚至超越了 3 位量化的 RTN 模型,验证了其在低比特场景下的优越性。
语言建模性能(困惑度)
表 2 展示了各方法在 LLaMA1&2&3 系列模型上的困惑度结果(困惑度越低,性能越好)。可以看出,ARB-LLM_X 和 ARB-LLM_RC 的困惑度显著低于 BiLLM,且无需增加权重比特数。例如,LLaMA-7B 模型中,ARB-LLM_RC 的 WikiText2 困惑度为 14.03,远低于 BiLLM 的 49.79;LLaMA-13B 模型中,ARB-LLM_RC 的困惑度为 13.38,优于 BiLLM 的 43.39。此外,ARB-LLM_RC 在 OPT-66B 模型上超越了 3 位量化的 GPTQ,进一步证明了其性能优势。
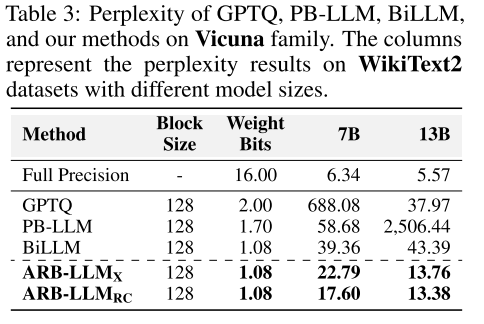
表 3 展示了各方法在 Vicuna 系列模型上的困惑度结果。可以看出,我们的方法在指令微调模型上仍保持显著优势,ARB-LLM_RC 的困惑度最低,验证了其在实际应用场景中的有效性。
表 2:GPTQ、PB-LLM、BiLLM 以及我们提出的方法在 LLaMA1&2&3 系列模型上的困惑度对比。列 WikiText2 和 C4 分别表示两个数据集的结果,数值越低越好。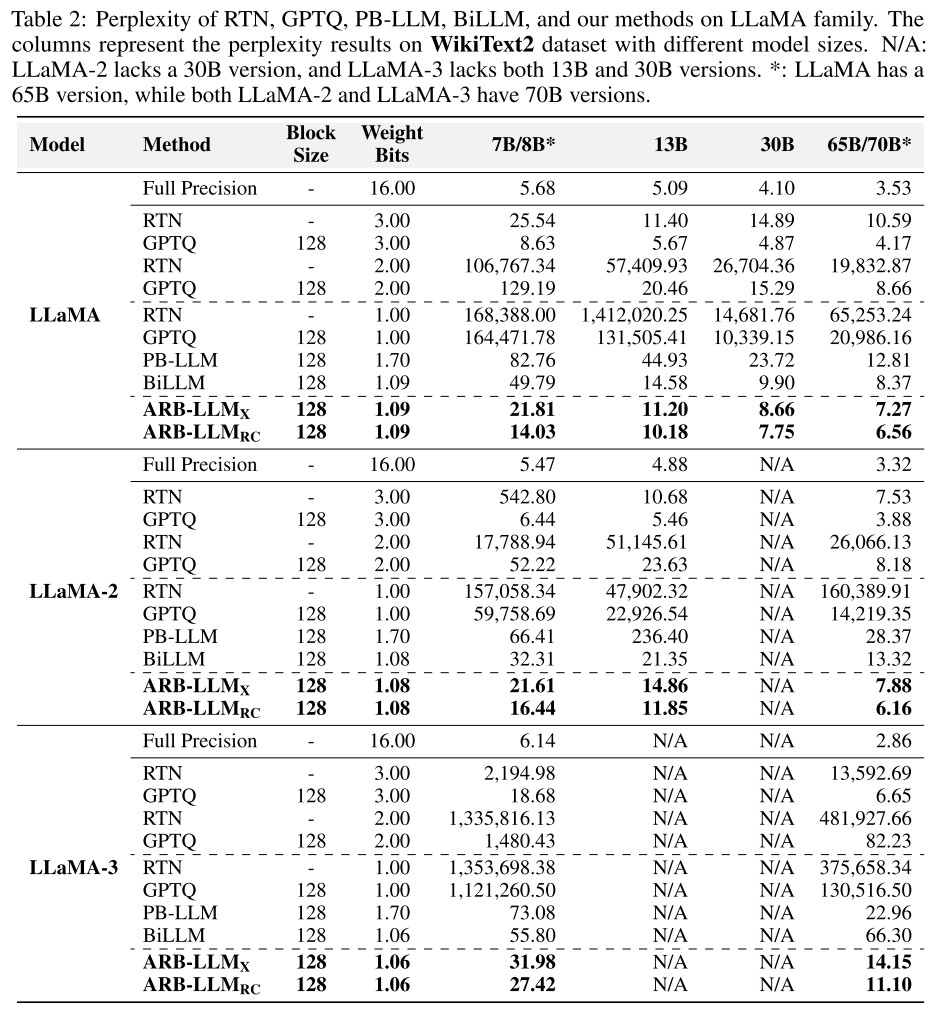
表 3:GPTQ、PB-LLM、BiLLM 以及我们提出的方法在 Vicuna 系列模型上的困惑度结果。列 WikiText2 代表不同模型尺寸下的数据集表现。
4.3 消融实验
高级变体的有效性
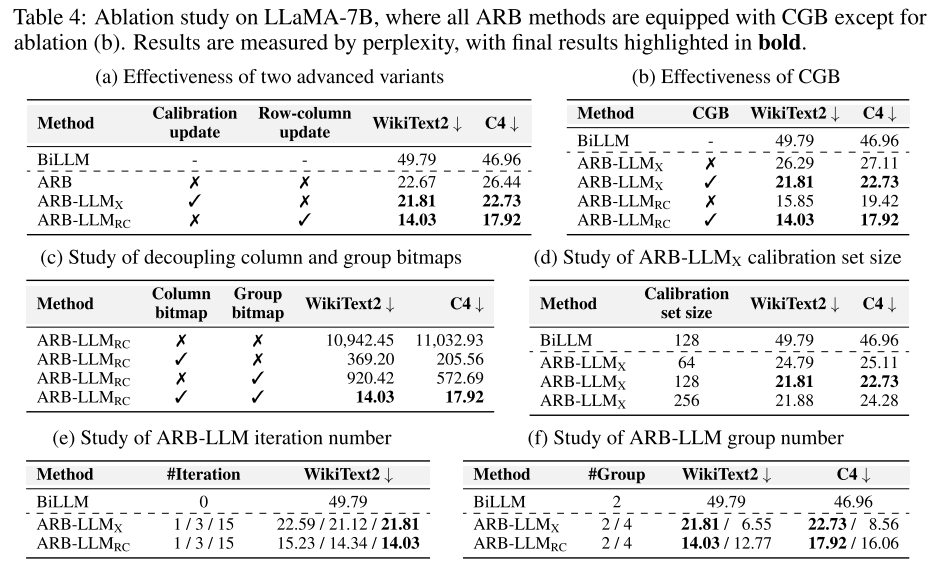
表 4(a)对比了基础 ARB 与两种高级变体(ARB-X、ARB-RC)的性能。可以看出,基础 ARB 已显著优于 BiLLM;而通过融入校准数据(ARB-X)或行列双向缩放(ARB-RC),性能进一步提升,验证了两种高级变体的设计合理性。其中,ARB-RC 的性能最优,表明行列双向缩放能更有效地捕捉大型语言模型的权重分布特征。
CGB 的有效性
表 4(b)展示了 CGB 对模型性能的影响。结果表明,无论是否配备 CGB,ARB 系列方法均优于 BiLLM;而配备 CGB 后,ARB-LLM_X 和 ARB-LLM_RC 的性能均得到进一步提升(例如,ARB-LLM_RC 的 WikiText2 困惑度从 15.85 降至 14.03)。这验证了 CGB 策略能有效优化权重划分,提升位图利用率。
列位图与组位图的协同作用
表 4(c)探索了列位图与组位图的单独作用和协同作用。结果表明,仅使用列位图或组位图会导致性能显著下降;完全不使用位图(#group=1,即朴素二值化)会导致模型完全失效(困惑度超过 10000)。这证明了列位图与组位图的协同作用对模型性能至关重要,CGB 策略通过优化两者的融合实现了性能提升。
校准集规模的影响
表 4(d)展示了校准集规模对 ARB-LLM_X 性能的影响。结果表明,校准集规模为 128 时性能最优;即使规模减小至 64,ARB-LLM_X 的性能仍显著优于 BiLLM(WikiText2 困惑度 24.79 vs 49.79);规模增大至 256 时,性能提升不明显。这表明我们的方法仅需少量校准数据即可实现优异性能,降低了实际应用中的数据依赖。
迭代次数的影响
表 4(e)展示了迭代次数对模型性能的影响。结果表明,即使仅迭代 1 次,ARB-LLM_X 和 ARB-LLM_RC 的性能仍优于 BiLLM;随着迭代次数增加(1→3→15),困惑度逐渐降低,15 次迭代后参数完全收敛。这验证了交替精炼策略的有效性,且迭代带来的额外计算开销可控。
分组数量的影响
表 4(f)展示了分组数量对模型性能的影响。结果表明,分组数量从 2 增加至 4 时,性能有所提升(例如,ARB-LLM_X 的 WikiText2 困惑度从 21.81 降至 6.55),但会带来额外存储开销(LLaMA-7B 模型增加约 0.8GB)。综合考虑性能与内存效率,我们选择 2 组作为默认配置。
表 4:在 LLaMA-7B 模型上的消融实验结果,除消融实验(b)外,所有 ARB 方法均配备 CGB。结果以困惑度衡量,最终结果用粗体突出显示。(a)两种高级变体的有效性(b)CGB 的有效性(c)列位图与组位图的解耦研究(d)ARB-LLM_X 校准集规模的影响(e)ARB-LLM 迭代次数的影响(f)ARB-LLM 分组数量的影响
4.4 时间与内存分析
时间对比
表 5 展示了 BiLLM 与 ARB-LLM 方法在 LLaMA-7B 模型上的时间消耗对比。作为二进制 PTQ 框架,ARB-LLM 无需微调;尽管交替算法需要额外计算以逐步对齐分布,但开销可控。例如,ARB-LLM_RC(15 次迭代)仅比 BiLLM 多耗时 21 分钟;无 CGB 的 ARB-LLM_RC(1 次迭代)仅多耗时 3 分钟。CGB 带来的额外时间开销源于最优划分的分位数搜索,在可接受范围内。

表 5:BiLLM 与我们的 ARB-LLM 方法在 LLaMA-7B 模型上的时间对比。
表 6:FP16、PB-LLM、BiLLM 与我们的 ARB-LLM 方法的内存对比。
内存对比
表 6 展示了各方法在 LLaMA-7B 和 LLaMA-13B 模型上的内存消耗对比。结果表明:
- ARB-LLM_X 与 BiLLM 内存消耗相同(LLaMA-7B 为 2.93GB),但性能显著更优;
- ARB-LLM_RC(无 CGB)的内存消耗最低(LLaMA-7B 为 2.63GB),比 BiLLM 低约 0.3GB,同时性能最优;
- 配备 CGB 后,ARB-LLM_RC 的内存消耗为 2.83GB(LLaMA-7B),仍低于 BiLLM,且性能大幅提升。
这验证了 ARB-LLM 在内存效率和性能之间的优异平衡,为大型语言模型的轻量化部署提供了高效解决方案。
5 结论
本文提出 ARB-LLM,一系列面向大型语言模型的交替精炼二值化方法。通过分析二值化与全精度权重的分布偏移,我们提出交替精炼二值化参数的策略,逐步对齐权重分布;基于基础 ARB 框架,融入校准数据和行列双向缩放因子,得到高级变体 ARB-X 和 ARB-RC;同时,通过列组位图(CGB)优化权重划分策略,提升位图利用率。在多个开源大型语言模型家族上的实验表明,最终模型 ARB-LLM_X 和 ARB-LLM_RC 显著优于现有最先进二进制训练后量化方法,其中 ARB-LLM_RC 首次实现了超越同尺寸 FP16 模型的性能,为大型语言模型的高效部署提供了新的技术路径。
未来工作可探索将 ARB 框架扩展至更低比特量化(如亚比特),并结合硬件优化实现端侧部署。