一、原理介绍
首先我们已知PMSM离散化电流模型
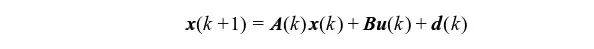
其中
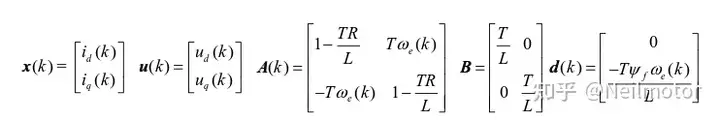
当考虑参数失配时,会得到电流预测值与电流实际值的误差如下
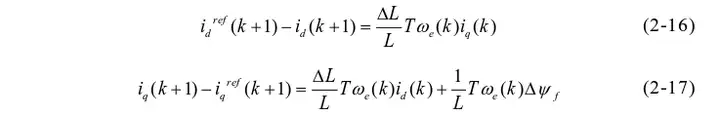
可以得出,控制器中磁链与实际磁链的误差只会对q轴电流造成静差,对d轴电流无影响。当电机正转,控制器中磁链大于实际值时,∆ψf>0,iq实际值大于指令; 当控制器中磁链小于实际值时,∆ψf<0,iq实际值小于指令。
为了消除磁链参数误差对控制器性能的影响,下面引入PMSM增量式模型
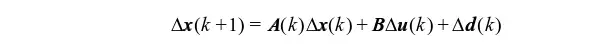
在转速进入稳态后,转子电角速度ωe保持不变,因此d(k)的增量可以表示如下:
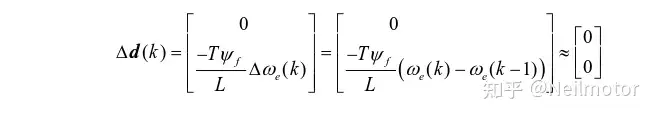
在暂态阶段,尤其是速度阶跃过程中,ωe的变化较快。然而,由于电机的机械时间常数远小于电气时间常数,在相邻的电流环采样周期内,电机转速可以认为相同。此外,多数情况下速度环的采样频率也要低于电流环的采样频率,此时在相邻的电流环周期内速度也为定值。
此外,永磁同步电机还是非线性、强耦合的系统。通过采用增量式模型, A(k)矩阵在相邻的电流环采样周期内也可以认为不变,因此A(k)可以写成A, 整个永磁同步电机模型可以看做线性模型。对于线性系统,状态方程等价于增量式状态方程,即:
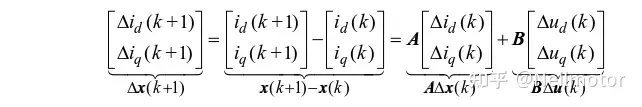
在上式中,唯一含有转子磁链ψf的矩阵d(k)被忽略了。因此采用增量式模型可以保证算法在无需磁链参数的情况下运行。此外,增量式模型不依赖于任何观测器或参数辨识策略,与其他方法相比更简便。
因此将增量式模型引入k+1时刻电流预测算法以及udq预测算法中。数字控制器中的1.5拍延迟已通过算法进行补偿。
二、仿真模型
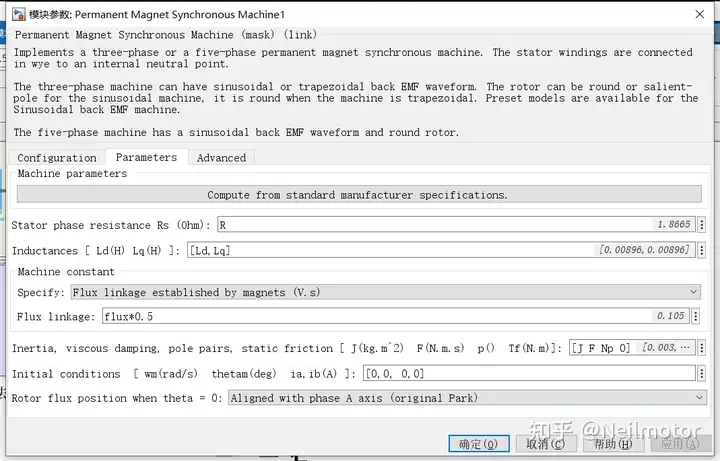
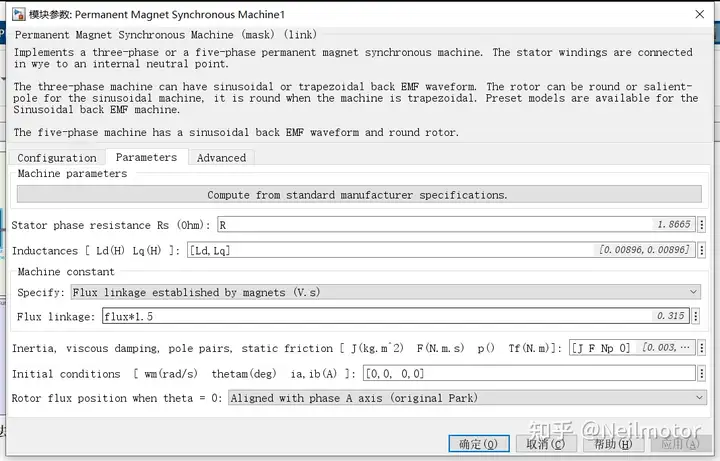
在MATLAB/simulink里面验证所提算法,搭建仿真。采用和实验中一致的采样、控制周期1e-4,电机部分计算周期为5e-7。仿真模型如下所示:
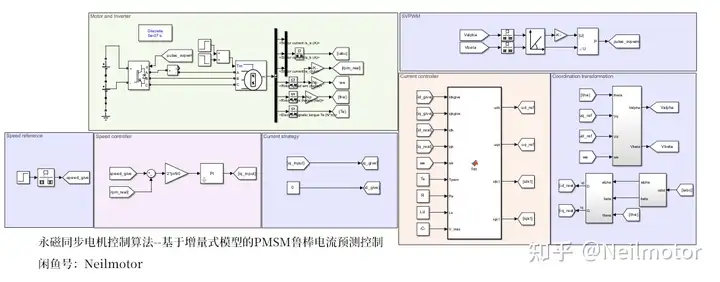
仿真工况:电机空载零速启动,给定转速为1000rpm,0.5s施加额定负载,1s撤掉负载。将传统DPCC(上)与基于增量式模型的鲁棒无差拍电流预测控制(下)进行对比。
2.1参数准确
转速
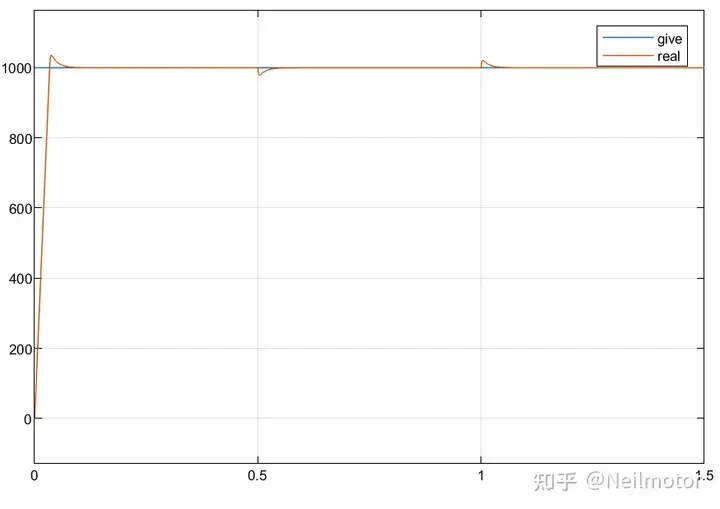
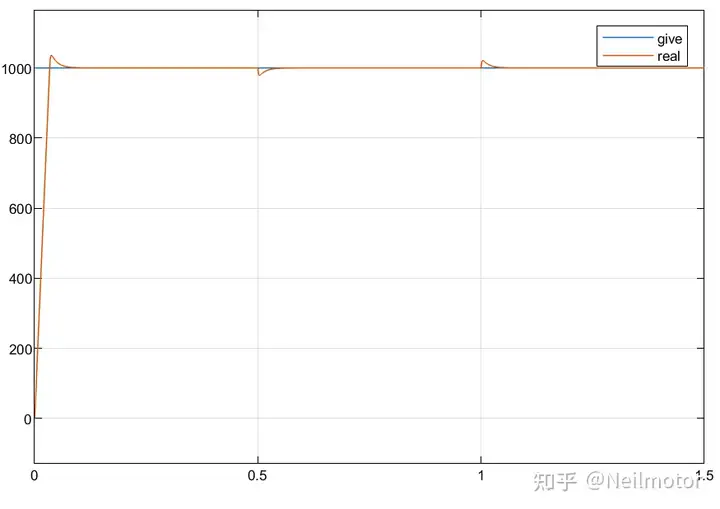
dq轴预测电流与实际电流
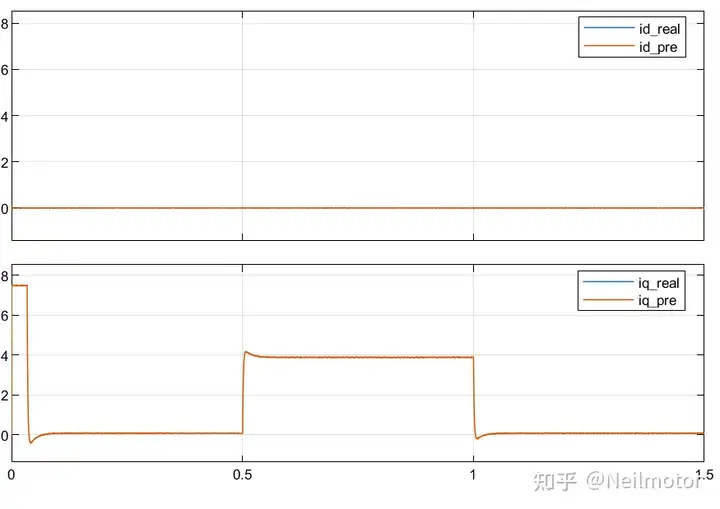
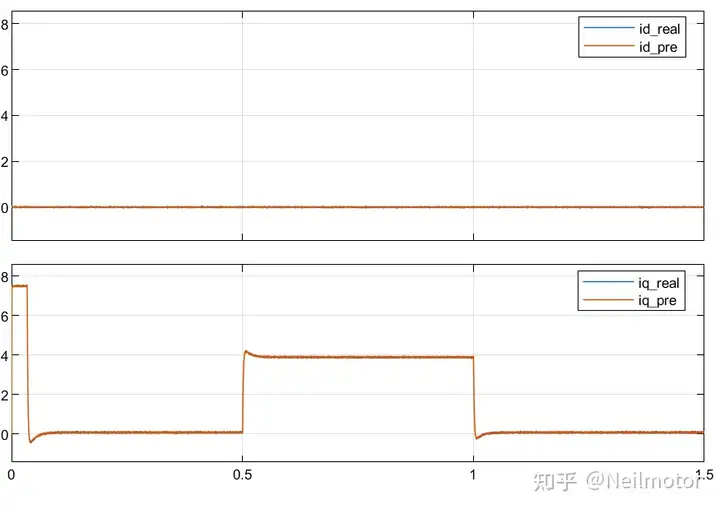
在参数准确时,两种算法的控制性能基本一致。
下面改变电机中设置的参数分别为0.5倍和1.5倍额定磁链,算法中保持1倍额定磁链,模拟磁链参数失配工况
2.2 0.5倍磁链
dq轴预测电流与实际电流
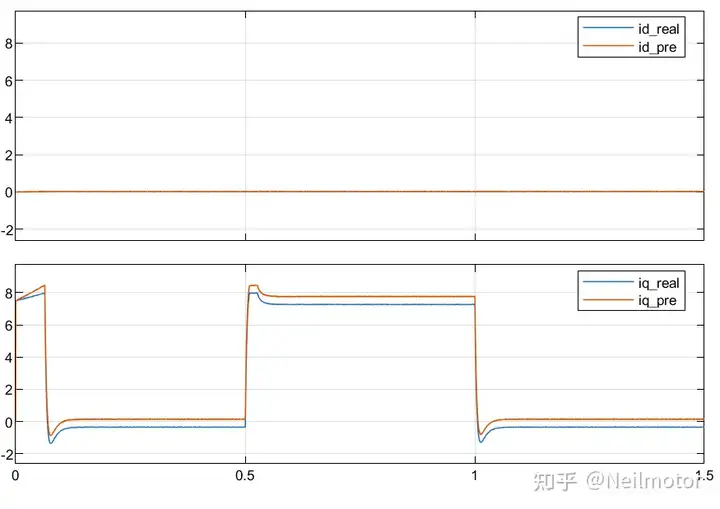
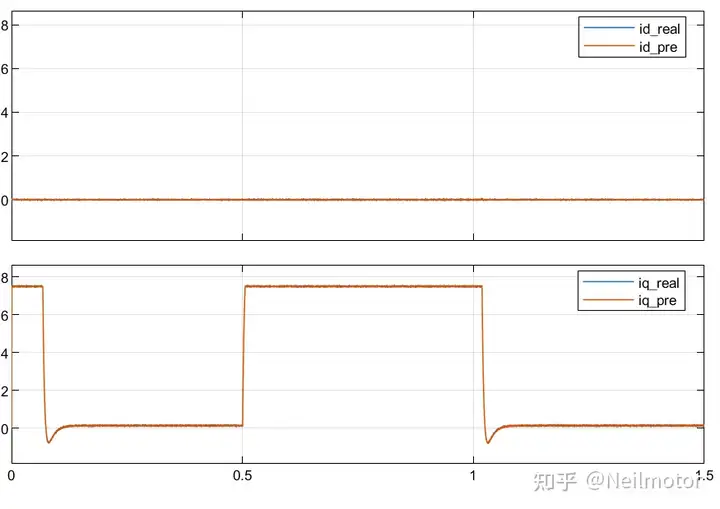
可能对比波形和理论分析,有人会疑惑,理论分析中"当电机正转,控制器中磁链大于实际值时,∆ψf>0,iq实际值大于指令;"而波形里面实际值更小。这是由于上图所示为电机反馈的实际值和MPC预测的电流值,下图才是实际值与控制器给出的指令,即iqref。也就是转速环控制器输出的控制量。可见实际效果与理论分析相符。
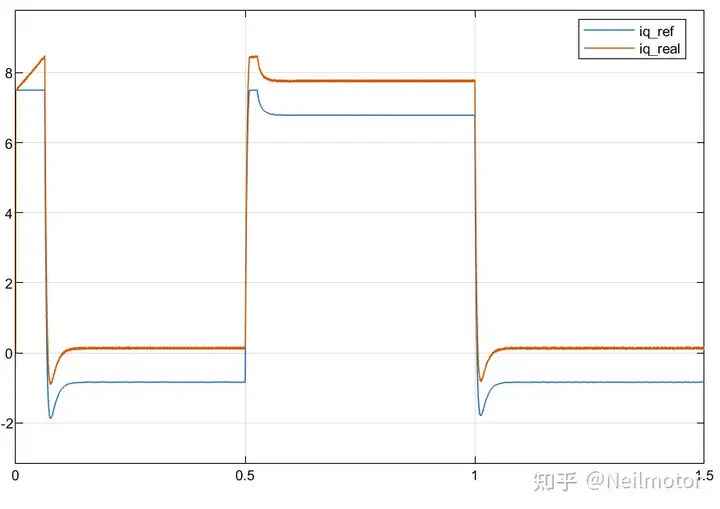
2.3 1.5倍磁链
dq轴预测电流与实际电流
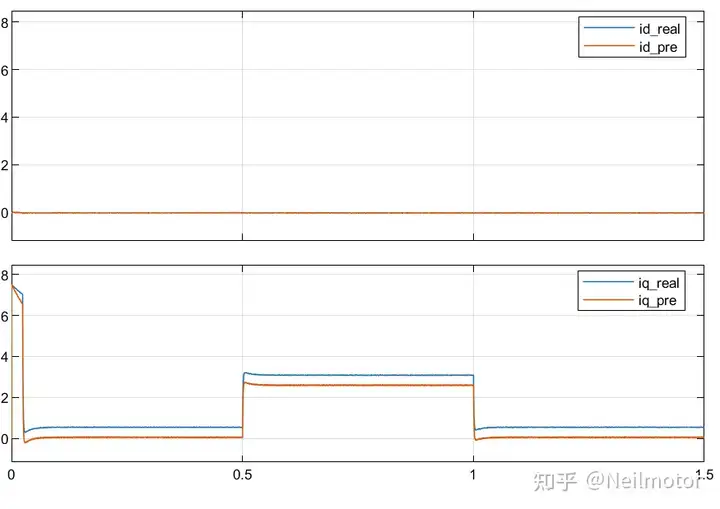
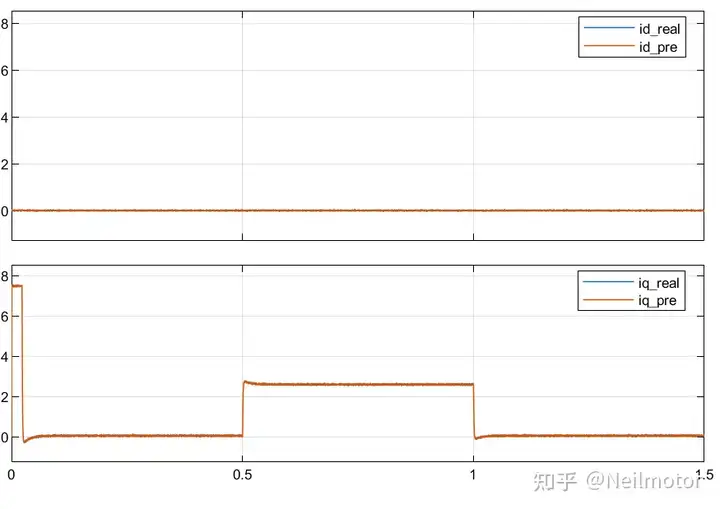
综上,可以看出增量式模型可以有效消除转子磁链参数失配对模型预测算法的干扰,而电阻项系数非常小,本身影响不大。电机电气参数中就剩下了电感,可以通过增加参数辨识算法或者观测器等方法来继续优化,后续也会继续更新这部分的方法。一句话理解增量式模型的作用就是:通过认为相邻两个控制周期转速不变,进而通过相减消除反电动势项(包含磁链的项),从而对磁链"脱敏"。增量式模型的算法可以拓展到其余类型模型预测算法中,比如有限集模型预测。