正态（高斯）分布（Gaussian distribution）

简介：个人学习分享，如有错误，欢迎批评指正。

高斯分布（Gaussian distribution）是描述连续随机变量的概率分布，广泛用于自然科学、统计学、工程学等领域。它由德国数学家高斯（Carl Friedrich Gauss）提出，最早用于描述天文数据中的误差。高斯分布在数学上也被称为正态分布（Normal distribution），具有许多优良的统计性质，并且适用于描述许多自然现象。

1.高斯分布的定义

高斯分布的概率密度函数（Probability Density Function, PDF）定义为：

f ( x ∣ μ , σ 2 ) = 1 2 π σ 2 exp ⁡ ( − ( x − μ ) 2 2 σ 2 ) f(x | \mu, \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left( - \frac{(x - \mu)^2}{2\sigma^2} \right) f(x∣μ,σ2)=2πσ2 1exp(−2σ2(x−μ)2)

其中：

• x x x 是随机变量，表示可能的观测值。
• μ \mu μ 是高斯分布的均值（mean），决定分布的中心位置。
• σ 2 \sigma^2 σ2 是方差 （variance），描述分布的宽度， σ \sigma σ 是标准差（standard deviation），其平方即为方差。标准差反映了数据的分散程度，标准差越大，数据分布越宽，反之则越窄。
• exp 是指数函数。
  

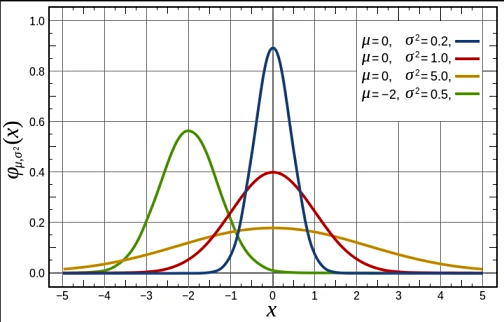
解释

1. 正态分布的形状 ：正态分布的图像呈钟形对称曲线，均值 μ \mu μ 是曲线的对称轴。大部分数据集中在均值附近，远离均值的概率逐渐减小，形成一个平滑的钟形曲线。曲线的高度由标准差 σ \sigma σ 控制，标准差越小，曲线越陡峭；标准差越大，曲线越平缓。

2. 常数因子 1 2 π σ 2 \frac{1}{\sqrt{2\pi \sigma^2}} 2πσ2 1：这一部分保证了整个曲线下面积为1，确保这是一个有效的概率密度函数。由于正态分布是连续分布，概率密度函数下的面积代表了事件的概率。

3. 指数部分 exp ⁡ ( − ( x − μ ) 2 2 σ 2 ) \exp\left( - \frac{(x - \mu)^2}{2\sigma^2} \right) exp(−2σ2(x−μ)2) ：该部分决定了数据点 x x x 离均值 μ \mu μ 越远，概率密度就越小。实际上，这部分是高斯分布最核心的特性，它确保了数据点接近均值时更可能发生，远离均值时发生的概率急剧减小。

2.高斯分布的性质

高斯分布具有以下几个重要性质：

1. 对称性 ：

   高斯分布是对称的，且对称轴为均值 μ \mu μ。这意味着在均值两侧，概率分布是完全一样的。

2. 均值、方差和标准差：

   • 均值 μ \mu μ 表示分布的中心，是数据集中最可能的值。它使得分布的中点与两侧的概率相等。
   • 方差 σ 2 \sigma^2 σ2 描述数据的离散程度，即数据点与均值的偏差的平方的期望值。方差越大，分布越宽；方差越小，分布越窄。
   • 标准差 σ \sigma σ 是方差的平方根，直接反映了数据的波动幅度。它是最常用来衡量数据分散程度的指标。

3. 68-95-99.7法则 （Empirical Rule）：

   这一法则指出，在标准正态分布中，约68%的数据点落在均值的1个标准差范围内，95%的数据点落在2个标准差范围内，99.7%的数据点落在3个标准差范围内。

   具体来说：

   • P ( μ − σ ≤ X ≤ μ + σ ) ≈ 68 P(\mu - \sigma \leq X \leq \mu + \sigma) \approx 68% P(μ−σ≤X≤μ+σ)≈68
   • P ( μ − 2 σ ≤ X ≤ μ + 2 σ ) ≈ 95 P(\mu - 2\sigma \leq X \leq \mu + 2\sigma) \approx 95% P(μ−2σ≤X≤μ+2σ)≈95
   • P ( μ − 3 σ ≤ X ≤ μ + 3 σ ) ≈ 99.7 P(\mu - 3\sigma \leq X \leq \mu + 3\sigma) \approx 99.7% P(μ−3σ≤X≤μ+3σ)≈99.7

4. 极限性质（中心极限定理） ：

   根据中心极限定理，若多个独立的随机变量遵循任意分布，当样本容量增大时，它们的和的分布会趋近于正态分布。因此，很多实际问题中，尽管数据并非直接遵循正态分布，经过加权平均等操作后，最终趋于正态分布。

5. 无穷分布 ：

   正态分布的概率密度函数在理论上是无限延伸的，意味着数据的取值范围是从负无穷到正无穷，但它在两侧的概率非常小。

3.标准正态分布

标准正态分布是均值为 0 0 0 且标准差为 1 1 1 的特殊正态分布。它的概率密度函数为：

f ( x ) = 1 2 π exp ⁡ ( − x 2 2 ) f(x) = \frac{1}{\sqrt{2\pi}} \exp\left( - \frac{x^2}{2} \right) f(x)=2π 1exp(−2x2)

标准正态分布常常用 Z Z Z 来表示。 Z Z Z 是标准正态分布的随机变量，满足以下条件：

• 均值 μ = 0 \mu = 0 μ=0
• 方差 σ 2 = 1 \sigma^2 = 1 σ2=1

对于标准正态分布，任何正态分布的随机变量 X X X 都可以通过标准化转换为标准正态分布：

Z = X − μ σ Z = \frac{X - \mu}{\sigma} Z=σX−μ

其中， μ \mu μ 是原始分布的均值， σ \sigma σ 是标准差。

4.高斯分布的多维扩展

当我们处理多个随机变量时，高斯分布可以扩展到多维空间。如果有 n n n 个随机变量组成的向量 X = ( X 1 , X 2 , ... , X n ) X = (X_1, X_2, \dots, X_n) X=(X1,X2,...,Xn)，它们服从 n n n 维的高斯分布（多元正态分布），其概率密度函数为：

f ( x 1 , x 2 , ... , x n ) = 1 ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 exp ⁡ ( − 1 2 ( X − μ ) T Σ − 1 ( X − μ ) ) f(x_1, x_2, \dots, x_n) = \frac{1}{(2\pi)^{n/2} |\Sigma|^{1/2}} \exp\left( -\frac{1}{2} (X - \mu)^T \Sigma^{-1} (X - \mu) \right) f(x1,x2,...,xn)=(2π)n/2∣Σ∣1/21exp(−21(X−μ)TΣ−1(X−μ))

其中：

• X = ( x 1 , x 2 , ... , x n ) X = (x_1, x_2, \dots, x_n) X=(x1,x2,...,xn) 是一个 ( n ) 维随机变量的向量。
• μ = ( μ 1 , μ 2 , ... , μ n ) \mu = (\mu_1, \mu_2, \dots, \mu_n) μ=(μ1,μ2,...,μn) 是 n n n-维均值向量。
• Σ \Sigma Σ 是 n × n n \times n n×n 的协方差矩阵，描述了不同随机变量之间的相关性。

5.高斯分布的应用

高斯分布在统计学、机器学习、物理学等领域有广泛应用。以下是一些典型的应用：

1. 误差分析 ：

   在实验中，误差通常会受到多种独立因素的影响，根据中心极限定理，这些误差大部分呈现正态分布。因此，正态分布常被用来建模测量误差、实验误差等。。

2. 自然现象建模 ：

   很多自然现象，如人的身高、体重、血压等都可以近似地看作是正态分布。对于这些数据，正态分布可以很好地描述它们的分布特点。

3. 金融模型 ：

   在金融领域，尤其是资产价格波动性和收益率的建模中，常假设收益服从正态分布。然而，实际情况可能会偏离正态分布（如出现厚尾现象），但高斯分布仍然是常用的基础模型。

4. 统计推断 ：

   正态分布是许多统计推断方法的基础。例如，假设检验、置信区间估计等都依赖于正态分布的假设。通过正态分布，我们可以推导出样本均值的分布，进行假设检验等。

5. 机器学习 ：

   高斯分布是许多机器学习算法的基础，例如高斯朴素贝叶斯分类器、支持向量机（SVM）中的高斯核函数等。此外，高斯过程回归（Gaussian Process Regression）是一种非常强大的非参数回归方法。在深度学习中，正态分布也常用于权重初始化、数据预处理等。

6. 信号处理 ：

   在信号处理领域，正态分布被用来描述高斯噪声。很多信号和图像处理中都假设噪声符合正态分布，通过这种假设，我们可以设计滤波器来去除噪声，增强信号。

为了更好地理解正态分布，我们可以通过一个具体的数学实例来展示它在实际问题中的应用。这个例子将帮助我们直观地了解正态分布是如何在实际数据中出现的。

6.实例：测量误差

假设我们要测量一块物体的长度，并且测量工具本身有误差。虽然理想情况下，物体的真实长度是一个确定的值 L L L，但由于各种因素（例如仪器精度、环境因素等），每次测量的结果都会有误差。这些误差通常会服从一个正态分布。

步骤 1：设定真实长度和误差模型

假设物体的真实长度 为 L = 10 L = 10 L=10 厘米。每次测量的误差 ϵ \epsilon ϵ 服从一个正态分布，均值为 0，标准差为 0.5 厘米，即：

ϵ ∼ N ( 0 , 0.5 2 ) \epsilon \sim N(0, 0.5^2) ϵ∼N(0,0.52)

这意味着每次测量的误差是围绕真实值 L = 10 L = 10 L=10 进行随机波动的，并且大多数误差会在 − 0.5 -0.5 −0.5 到 0.5 0.5 0.5 厘米的范围内波动。

步骤 2：计算测量值的分布

每次测量的实际结果 X X X 等于真实长度 L L L 加上误差 ϵ \epsilon ϵ：

X = L + ϵ = 10 + ϵ X = L + \epsilon = 10 + \epsilon X=L+ϵ=10+ϵ

因此，测量值 X X X 的分布是：

X ∼ N ( 10 , 0.5 2 ) X \sim N(10, 0.5^2) X∼N(10,0.52)

即，测量结果 X X X 服从均值为 10 10 10 厘米、标准差为 0.5 厘米的正态分布。

步骤 3：模拟测量

我们进行多次测量，假设我们进行 1000 次独立的测量，每次测量的误差 ϵ \epsilon ϵ 都来自于正态分布 N ( 0 , 0.25 ) N(0, 0.25) N(0,0.25)，并计算每次的测量值 X X X。

1. 在每次测量中，随机生成一个误差 ϵ \epsilon ϵ。
2. 每次测量的结果 X X X 由 X = 10 + ϵ X = 10 + \epsilon X=10+ϵ 给出。

假设我们生成了 1000 次测量结果并绘制其直方图。我们会看到这些测量值大致遵循一个正态分布，均值接近于 10 厘米（即真实长度），标准差接近于 0.5 厘米。

步骤 4：正态分布的性质

根据正态分布的性质，我们可以预计大多数的测量值将会集中在均值附近，具体来说：

• 68%的测量值 会在 [ 10 − 0.5 , 10 + 0.5 ] = [ 9.5 , 10.5 ] [10 - 0.5, 10 + 0.5] = [9.5, 10.5] [10−0.5,10+0.5]=[9.5,10.5] 厘米的范围内。
• 95%的测量值 会在 [ 10 − 1 , 10 + 1 ] = [ 9 , 11 ] [10 - 1, 10 + 1] = [9, 11] [10−1,10+1]=[9,11] 厘米的范围内。
• 99.7%的测量值 会在 [ 10 − 1.5 , 10 + 1.5 ] = [ 8.5 , 11.5 ] [10 - 1.5, 10 + 1.5] = [8.5, 11.5] [10−1.5,10+1.5]=[8.5,11.5] 厘米的范围内。

这意味着大多数测量值都会在真实长度 10 厘米的附近，并且误差会遵循一个正态分布，较大的误差发生的概率会随着误差的增大而急剧减少。

步骤 5：理论与实际结果的比较

1. 理论 ：

   根据正态分布的理论，测量值 X X X 的分布应该是一个均值为 10，标准差为 0.5 的正态分布。

2. 实际 ：

   通过多次模拟测量，我们可以绘制测量值的直方图。结果应该接近理论正态分布，尤其是随着测量次数增多，测量结果的分布会越来越接近正态分布。

结论

通过这个例子，我们证明了正态分布在实际问题中的应用：即使我们的原始数据（测量误差）本身不是正态分布，随着样本量的增大，误差的分布会趋近于正态分布。这也验证了中心极限定理的作用：即使单个误差不服从正态分布，多个独立误差的累积会形成正态分布。通过这种方式，正态分布在现实世界的误差分析中起到了重要作用。

这个例子展示了如何通过正态分布建模实际测量问题，并通过模拟和理论预测正态分布的性质与实际结果的一致性。

7.总结

高斯分布是一个非常重要的概率分布，其定义通过均值和方差完全确定。它的对称性、平滑性以及中心极限定理的性质使得它在很多领域成为常见的假设模型。高斯分布的核心公式为：

f ( x ∣ μ , σ 2 ) = 1 2 π σ 2 exp ⁡ ( − ( x − μ ) 2 2 σ 2 ) f(x | \mu, \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left( - \frac{(x - \mu)^2}{2\sigma^2} \right) f(x∣μ,σ2)=2πσ2 1exp(−2σ2(x−μ)2)

了解高斯分布的性质和应用，对于统计推断、数据分析及各类实际问题的建模都具有重要意义。

参考文献
一文搞懂"正态分布"所有需要的知识点
正态分布
正态分布（高斯分布）

结~~~