文章目录
一、前言
脉冲编码调制(Pulse Code Modulation, PCM) 是连续时间模拟信号进入数字通信系统时最基础也最核心的表示方式之一,其关键环节包括采样、量化与编码。在实际工程中,量化器的设计直接决定了量化噪声的统计特性以及重构信号的主观/客观质量。经典的均匀量化由于结构简单、实现代价低,在多类信号场景下具有良好的可用性;但对于幅度分布高度非均匀、弱信号段占比显著的语音类信号而言,均匀量化往往会造成弱信号细节被"粗粒度"覆盖,从而引入更明显的失真 。基于压扩思想(Companding)的非均匀量化由此成为语音通信系统中的重要方案,其中 μ-law 压缩(μ=255)在北美/日本标准体系内具有代表性。
本文围绕"PCM均匀量化与 μ-law 非均匀量化的性能差异"这一典型问题,构建一套可复现实验流程:以多正弦叠加信号近似模拟语音信号的基频与谐波结构,在电话语音常用采样率下进行采样与量化,并从量化误差与信噪比两条主线出发,给出多维度的仿真对比与现象解释。为了便于大家直观理解量化器的工作机理,程序还生成并保存一组覆盖"信号---量化---误差---指标---特性曲线"的分析图,用以揭示均匀量化与 μ-law 量化在小信号段与大信号段的差异来源。
二、程序整体功能概述
本文对应的仿真程序以 MATLAB 为实现环境,目标并非仅给出单一指标的数值比较,而是建立一套从算法流程到可视化证据链较为完整的 PCM 量化对比框架。总体而言,程序完成如下工作:首先在给定采样频率与持续时间条件下生成归一化到 [ − 1 , 1 ] [-1,1] [−1,1] 的多正弦叠加测试信号,并构造连续时间参考波形用于绘图对照;随后对离散采样序列分别施加均匀量化与 μ-law 非均匀量化。对于 μ-law 方案,程序按照 "压缩→均匀量化→扩展" 的标准思路实现,即先利用 μ-law 压缩函数将幅度动态范围进行非线性映射,再对压缩域信号执行均匀量化,最后通过扩展函数还原至原幅度域。
在性能评价层面,程序围绕两类常用指标展开。一方面给出量化误差序列 e [ n ] = x [ n ] − x ^ [ n ] e[n]=x[n]-\hat{x}[n] e[n]=x[n]−x^[n],并进一步计算均方根误差(RMSE)以反映总体误差能量:
R M S E = 1 N ∑ n = 1 N e 2 [ n ] \mathrm{RMSE}=\sqrt{\frac{1}{N}\sum_{n=1}^{N}e^2[n]} RMSE=N1n=1∑Ne2[n] 另一方面以信噪比(SNR)刻画量化前后信号与误差的功率关系:
S N R = 10 log 10 ( E x 2 [ n ] E e 2 [ n ] ) \mathrm{SNR}=10\log_{10}\left(\frac{\mathbb{E}{x^2[n]}}{\mathbb{E}{e^2[n]}}\right) SNR=10log10(Ee2[n]Ex2[n])为揭示量化性能随系统配置与信号幅度变化的规律,程序不仅固定 8-bit 进行"误差形态---统计分布---局部阶梯"的细致展示,还进一步在 4-bit、6-bit、8-bit 三种量化位数下扫描信号幅度区间(0.1 到 1.0),形成 SNR 曲线与相对增益曲线,从而使对比结论具有更强的可解释性。
三、仿真设置与方法
仿真参数的设定遵循"可复现、易解释、接近语音通信常用配置"的原则。采样频率取 f s = 8000 Hz f_s=8000\ \text{Hz} fs=8000 Hz,对应电话语音常用采样率;信号持续时间取 T = 20 ms T=20\ \text{ms} T=20 ms,从而得到 N = f s T = 160 N=f_sT=160 N=fsT=160 个采样点,能够覆盖多个基频周期并便于观察量化阶梯与误差变化。测试信号采用多正弦叠加形式,包含基频与若干谐波分量 300 H z 、 600 H z 、 900 H z 、 1200 H z 300 Hz、600 Hz、900 Hz、1200 Hz 300Hz、600Hz、900Hz、1200Hz,并将结果归一化到 [ − 1 , 1 ] [-1,1] [−1,1] 区间,以保证不同量化位数下比较时量程一致、饱和风险可控。该信号在频谱结构上具备"基音+谐波"的特征,可用于近似展示语音类信号在短时窗内的典型波形形态。
在量化器设定方面,程序对两种典型方案进行并行实现。均匀量化的核心在于将连续幅值映射到 L = 2 b L=2^b L=2b 个离散电平(其中 b b b 为量化位数),并以相邻电平等间隔为特征。为展示位数变化带来的趋势性影响,程序选取 b ∈ 4 , 6 , 8 b\in{4,6,8} b∈4,6,8 进行对比,并在 8-bit 条件下进行更细致的波形局部放大与误差统计。μ-law 非均匀量化则引入压扩机制,其压缩函数可写为
y = s g n ( x ) ⋅ ln ( 1 + μ ∣ x ∣ ) ln ( 1 + μ ) y=\mathrm{sgn}(x)\cdot\frac{\ln(1+\mu|x|)}{\ln(1+\mu)} y=sgn(x)⋅ln(1+μ)ln(1+μ∣x∣)其中 μ = 255 \mu=255 μ=255 为常用配置。压缩后的 y y y 进入均匀量化器,量化输出再经扩展函数恢复到幅度域。由此形成的等效量化电平在原幅度域呈现"零附近密集、远离零稀疏"的分布特征,这一点也通过程序的电平分布图与压缩特性曲线得以直观验证。
四、关键代码片段
1、生成测试信号
matlab
% 包含基频和谐波成分,幅度逐渐衰减
f1 = 300; % 基频
f2 = 600; % 二次谐波
f3 = 900; % 三次谐波
f4 = 1200; % 四次谐波
% 原始模拟信号(归一化到[-1, 1])
x_analog = 0.5*sin(2*pi*f1*t) + 0.3*sin(2*pi*f2*t) + ...
0.15*sin(2*pi*f3*t) + 0.05*sin(2*pi*f4*t);
x_analog = x_analog / max(abs(x_analog)); % 归一化
% 生成连续时间信号用于绘图
t_continuous = 0:1/(fs*10):T-1/(fs*10);
x_continuous = 0.5*sin(2*pi*f1*t_continuous) + 0.3*sin(2*pi*f2*t_continuous) + ...
0.15*sin(2*pi*f3*t_continuous) + 0.05*sin(2*pi*f4*t_continuous);
x_continuous = x_continuous / max(abs(x_continuous));2、量化函数定义
matlab
% 均匀量化函数
uniform_quantize = @(x, L) round((x + 1) / 2 * (L - 1)) / (L - 1) * 2 - 1;
% μ-law压缩函数
mu_law_compress = @(x, mu) sign(x) .* log(1 + mu * abs(x)) / log(1 + mu);
% μ-law扩展函数
mu_law_expand = @(y, mu) sign(y) .* ((1 + mu).^abs(y) - 1) / mu;3、8-bit量化详细分析
matlab
bit = 8;
L = 2^bit; % 量化电平数
% 均匀量化
x_uniform = uniform_quantize(x_analog, L);
% 非均匀量化(μ-law)
x_compressed = mu_law_compress(x_analog, mu); % 压缩
x_compressed_quantized = uniform_quantize(x_compressed, L); % 均匀量化
x_mulaw = mu_law_expand(x_compressed_quantized, mu); % 扩展还原
% 量化误差
error_uniform = x_analog - x_uniform;
error_mulaw = x_analog - x_mulaw;4、不同量化位数下的SNR对比
matlab
% 测试不同幅度的信号
amplitude_range = 0.1:0.1:1.0;
SNR_uniform = zeros(length(bits), length(amplitude_range));
SNR_mulaw = zeros(length(bits), length(amplitude_range));
for b = 1:length(bits)
bit_num = bits(b);
L_num = 2^bit_num;
for a = 1:length(amplitude_range)
amp = amplitude_range(a);
% 生成测试信号
x_test_signal = amp * x_analog;
% 均匀量化
x_uni = uniform_quantize(x_test_signal, L_num);
err_uni = x_test_signal - x_uni;
% μ-law量化
x_comp = mu_law_compress(x_test_signal, mu);
x_comp_q = uniform_quantize(x_comp, L_num);
x_mu = mu_law_expand(x_comp_q, mu);
err_mu = x_test_signal - x_mu;
% 计算SNR
signal_power = mean(x_test_signal.^2);
SNR_uniform(b, a) = 10 * log10(signal_power / mean(err_uni.^2));
SNR_mulaw(b, a) = 10 * log10(signal_power / mean(err_mu.^2));
end
end五、实验仿真结果
原始波形和采样后的离散信号
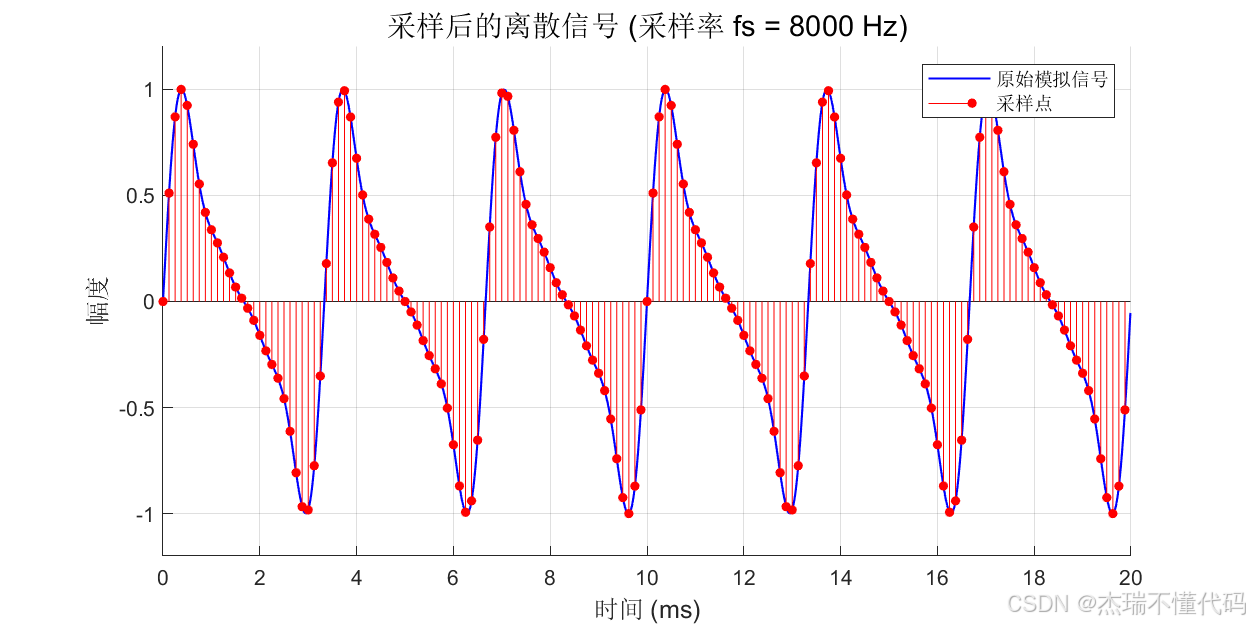
均匀量化后的波形
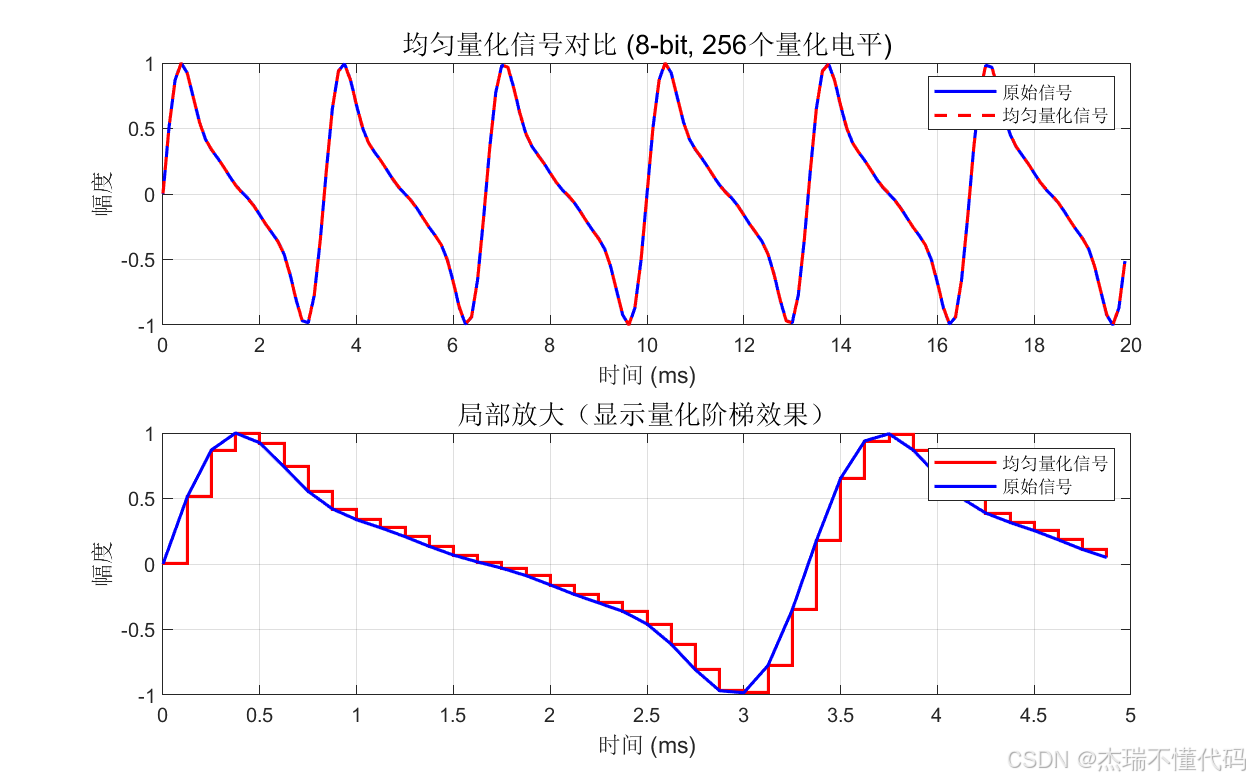
非均匀量化后的波形
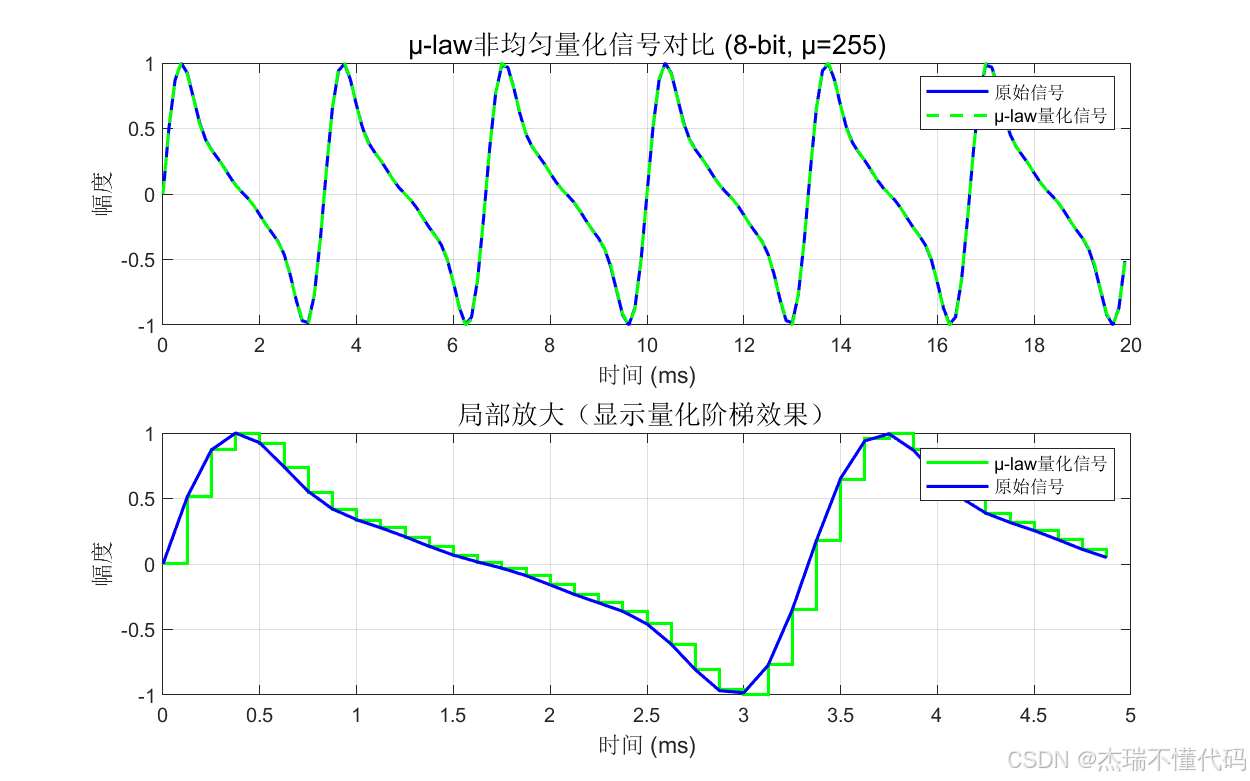
量化误差对比图
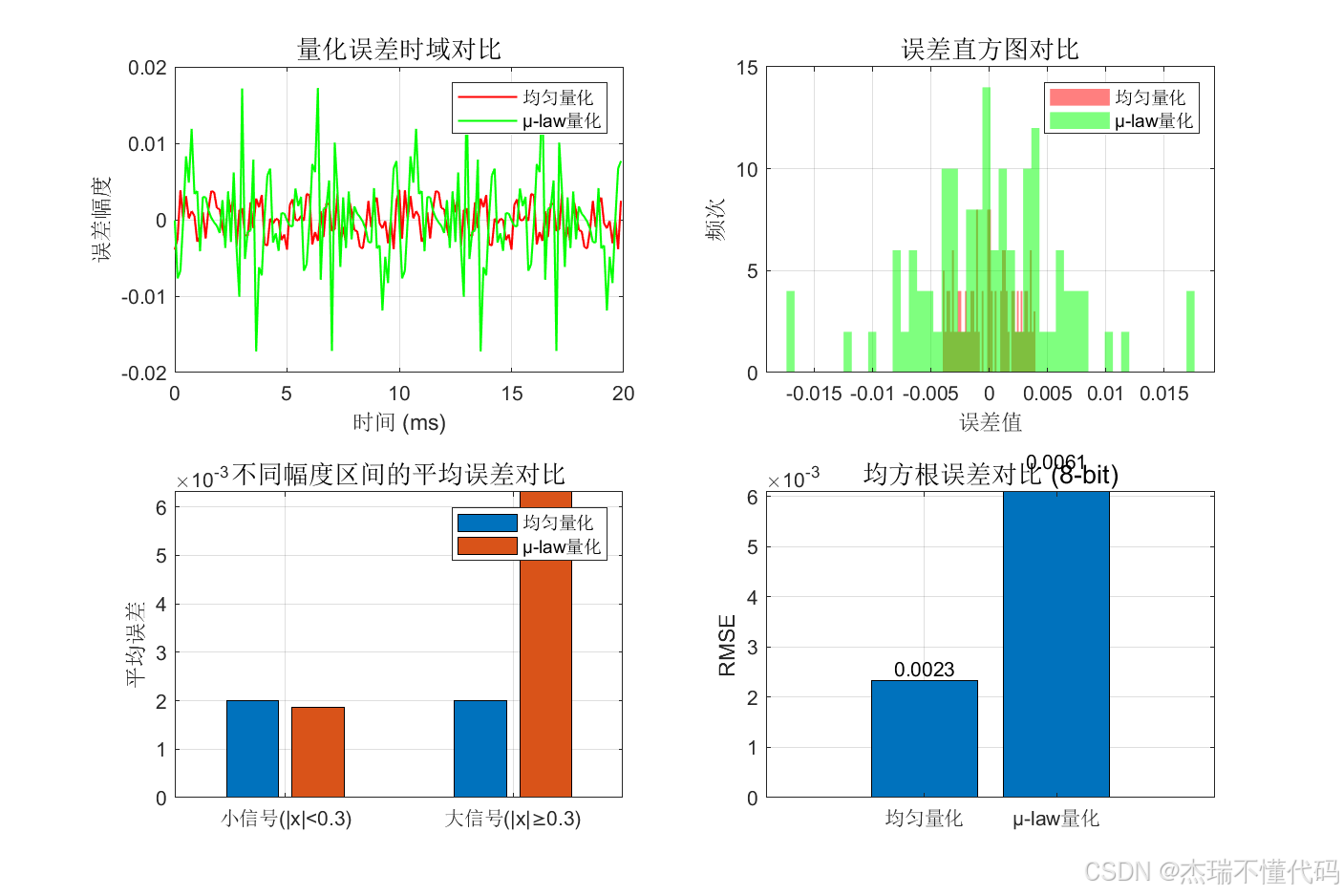
不同量化位数SNR对比曲线
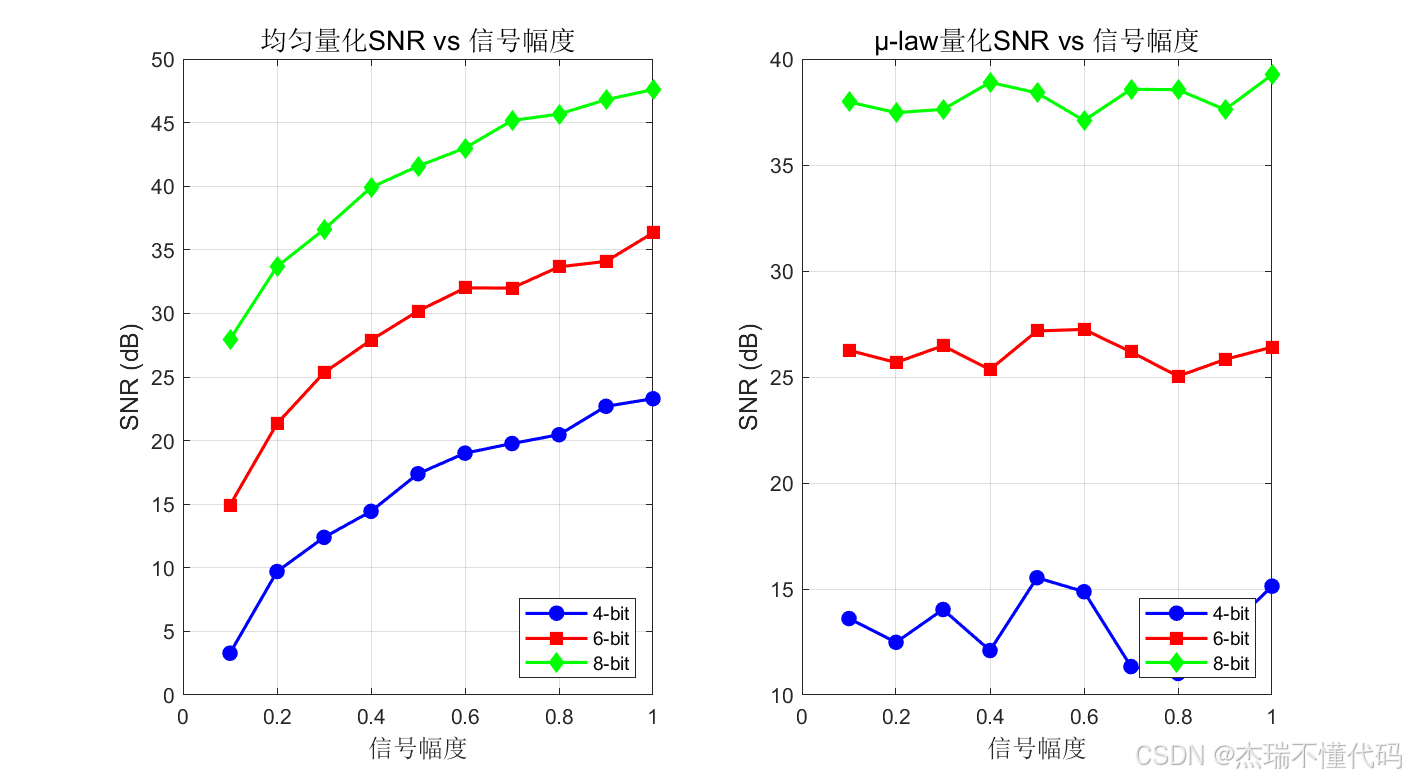
均匀量化和非均匀量化直观对比图
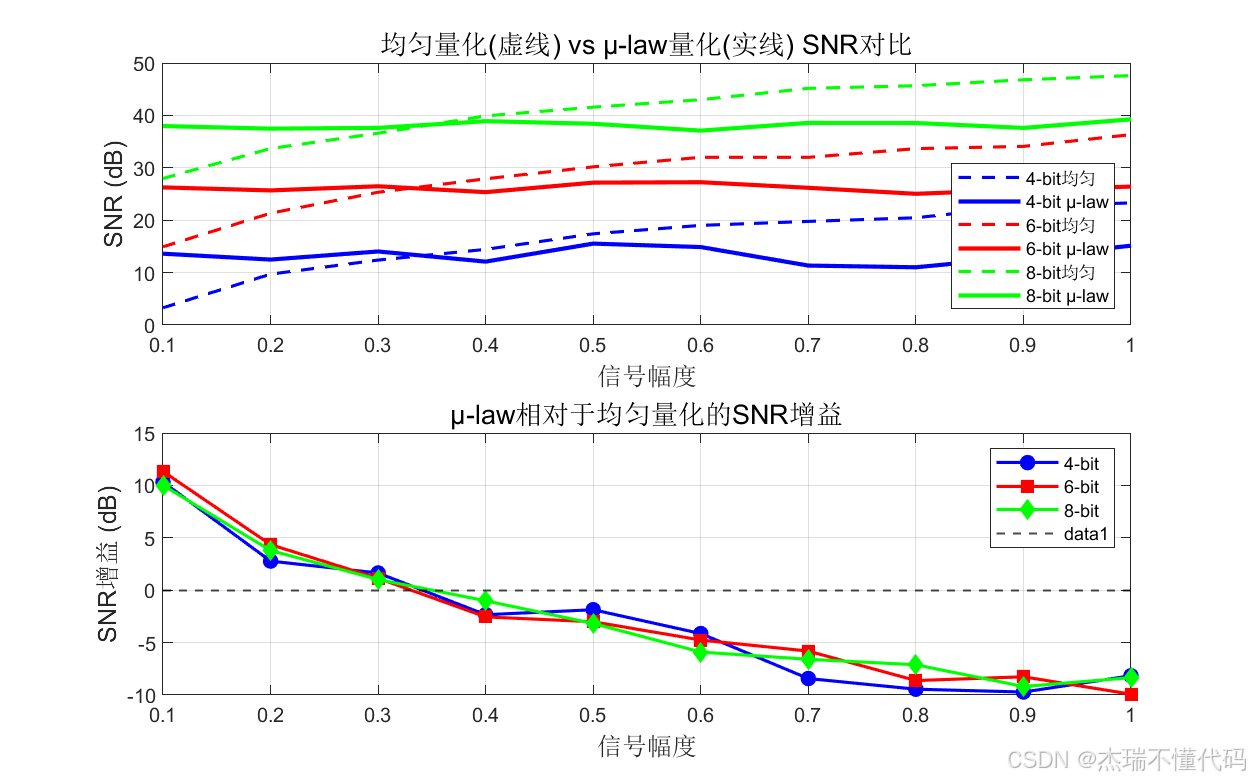
小信号情况下的对比图
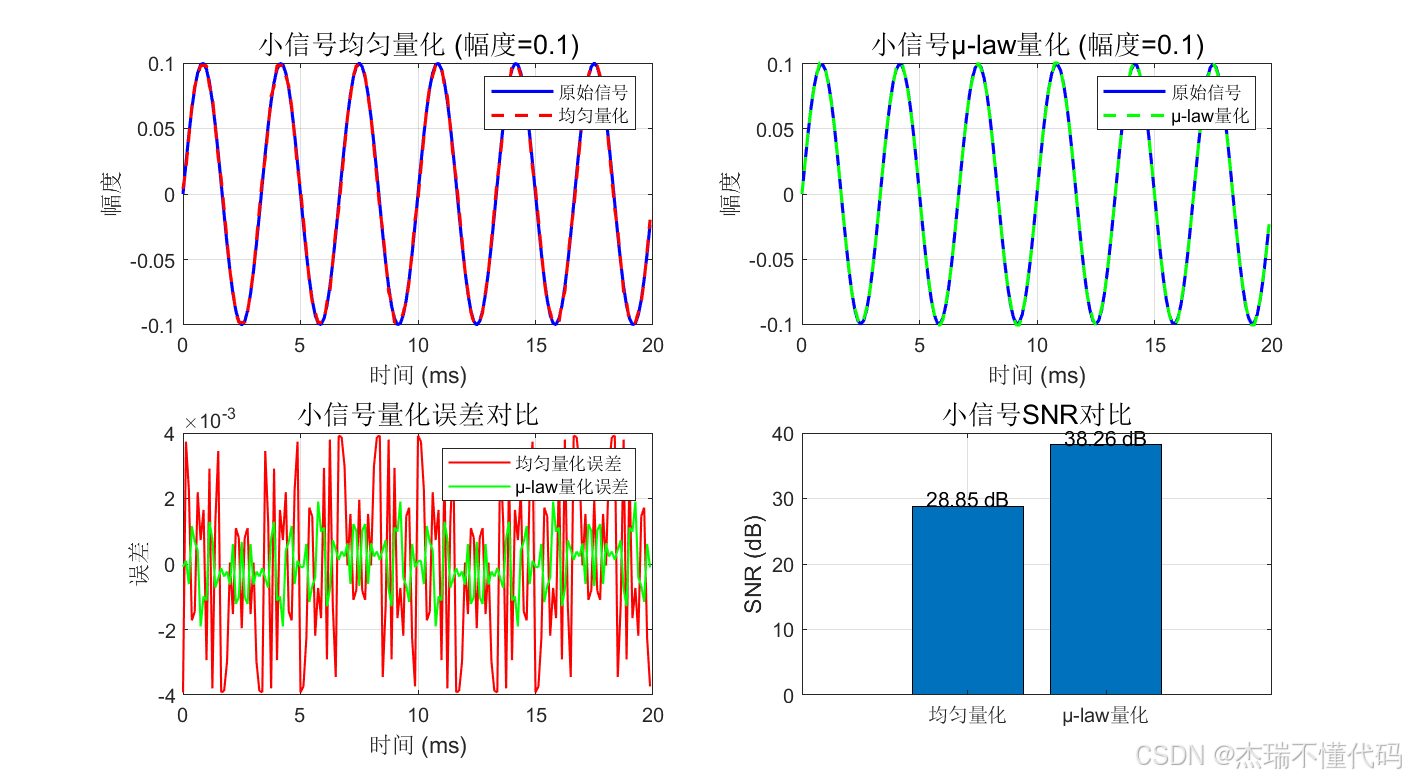
图片太多啦,看一张总览吧~
需要注意的是:μ-law 非均匀量化并非以最小均方误差为目标,而是通过对小幅度信号进行更精细的量化来提高弱信号的信噪比,因此在全幅度平均意义下,其 RMSE 可能大于均匀量化,但在小信号区域具有明显优势。
由于源代码很长,无法直接全部粘在这,因此挑了一些关键的部分予以展示,如果你对完整源码、可运行工程文件或拓展版本 感兴趣,欢迎留言交流,后续也会继续分享更多通信系统仿真相关内容,我是不懂代码的杰瑞学长,我们下期再见!
如果觉得文章对你有帮助,欢迎点赞 + 收藏 + 关注,一起进步!