一、机器学习核心任务分类
(配图1:机器学习三大核心任务对比图)
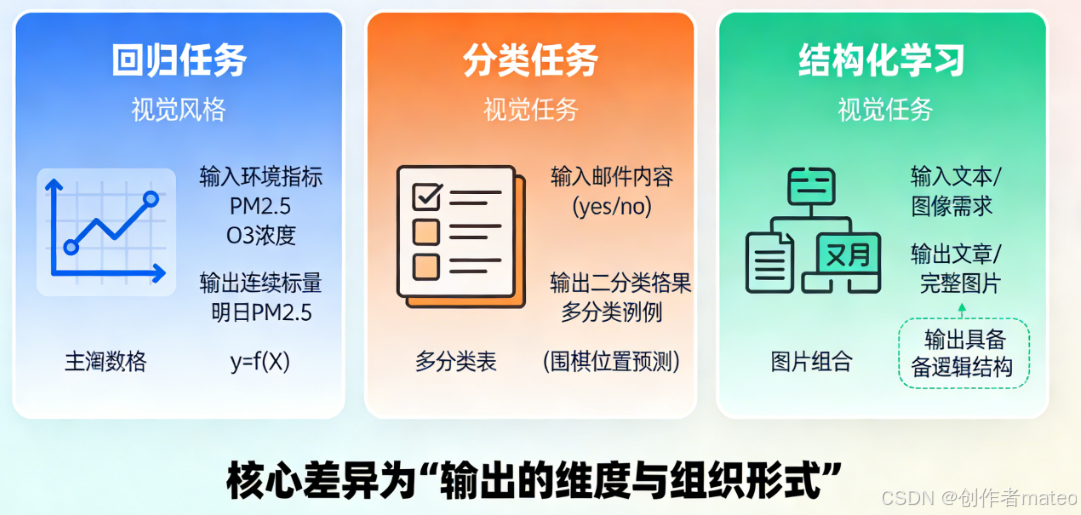
图注:机器学习的核心任务可根据输出形态分为三类:回归任务输出连续标量(如PM2.5预测);分类任务输出离散类别(如垃圾邮件判断);结构化学习输出具备逻辑或空间结构的结果(如文本、图像生成)。三者的核心差异在于输出的维度与组织形式。
机器学习的本质是找到合适的函数fff,将输入映射为符合任务需求的输出。根据输出形式的不同,核心任务主要分为三类:
1.1 回归(Regression)
- 定义 :函数的输出为标量(scalar),也就是单一的连续数值,主要用于预测连续型变量。
- 数学表达 :可以简单表示为y=f(X)y = f(X)y=f(X),其中XXX是输入的特征向量(比如环境指标、时序数据),yyy是待预测的连续目标值。
- 实际案例 :根据今日的PM2.5PM2.5PM2.5浓度、臭氧(O3O_3O3)浓度等环境数据,预测明日的PM2.5PM2.5PM2.5数值,具体映射关系为f(今日PM2.5、O3浓度)→明日PM2.5f(\text{今日}PM2.5、O_3浓度) \rightarrow \text{明日}PM2.5f(今日PM2.5、O3浓度)→明日PM2.5。此时函数输出的是具体的PM2.5PM2.5PM2.5数值,是典型的回归任务。
1.2 分类(Classification)
- 定义 :给定预设的选项(类别/classes),函数从这些类别中输出正确的结果,用于解决离散型的类别预测问题,又可分为二分类和多分类。
- 细分类型与案例 :
- 二分类(Binary Classification) :将样本划分为两个互斥的类别。最常见的例子是垃圾邮件过滤(spam filtering) :输入邮件内容,函数输出
yes或no,以此判断邮件是否为垃圾邮件,即f(邮件内容)→yes/nof(\text{邮件内容}) \rightarrow yes/nof(邮件内容)→yes/no。 - 多分类(Multi-class Classification) :将样本划分为两个以上的类别。比如围棋位置预测(playing Go):输入棋局状态,函数输出棋盘上的具体位置------棋盘上的每个位置对应一个独立类别,模型需要从众多类别中选出正确的位置。
- 二分类(Binary Classification) :将样本划分为两个互斥的类别。最常见的例子是垃圾邮件过滤(spam filtering) :输入邮件内容,函数输出
1.3 结构化学习(Structured Learning)
- 定义 :生成具有特定结构的输出,属于机器学习中的"创造类任务"。和回归、分类不同,它的输出不是单一数值或类别,而是带有逻辑关系的结构化对象(如序列、层级、空间结构)。
- 核心特征:输出结果具备上下文逻辑、空间布局、层级关系等结构化属性。
- 应用场景:文本生成(比如创作一篇逻辑连贯的文章)、图像生成(生成构图合理的完整图片)、分子结构预测(预测化学分子的空间结构)等,都属于结构化学习的范畴。简单来说,就是让机器根据输入创造出有结构的结果。
二、机器学习模型构建三步骤(案例分析)
(配图2:网页点击量预测模型三步构建流程图)
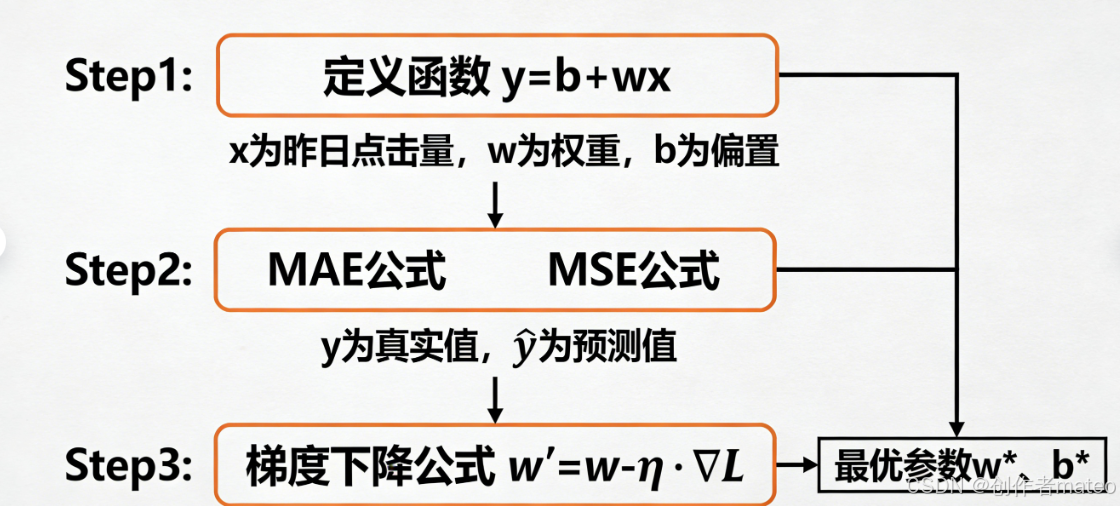
图注:以网页点击量预测为例,机器学习模型构建遵循固定逻辑:Step1 基于领域知识定义含未知参数的线性函数 y=b+wxy=b+wxy=b+wx;Step2 选用MAE或MSE作为损失函数,衡量预测值与真实值的差距;Step3 通过梯度下降迭代优化,找到使损失最小的最优参数 w∗,b∗w^*,b^*w∗,b∗。
以"预测网页总点击量"为例,讲解构建机器学习模型的核心三步骤,这也是搭建几乎所有ML模型的基础逻辑:
Step 1:定义含未知参数的函数
- 目标函数初始形式 :针对网页点击量预测任务,先定义抽象的函数形式为y=f(网站资讯、日期、订阅数)y = f(\text{网站资讯、日期、订阅数})y=f(网站资讯、日期、订阅数),其中yyy代表待预测的网页总点击量。
- 简化线性模型 :为降低问题复杂度,选取"昨日点击量"作为核心特征,用线性模型进行初步拟合,公式为y=b+wxy = b + wxy=b+wx。
- 参数说明 :
- yyy:今日网页点击量(模型的预测值/model output);
- xxx:昨日网页点击量(真实的观测数据/feature);
- bbb(偏置项/Bias):线性模型的截距,用于调整预测结果的基准线;
- www(权重/Weight):特征的权重,代表特征xxx对预测值yyy的影响程度。
- 参数设定依据 :bbb和www的初始值可以结合**领域知识(domain knowledge)**设定(比如根据网站历史点击规律,假设昨日点击量的权重为0.8),后续再通过优化步骤不断调整。
- 参数说明 :
Step 2:基于训练数据定义损失函数(Loss Function)
(配图3:MAE与MSE误差计算对比示意图)
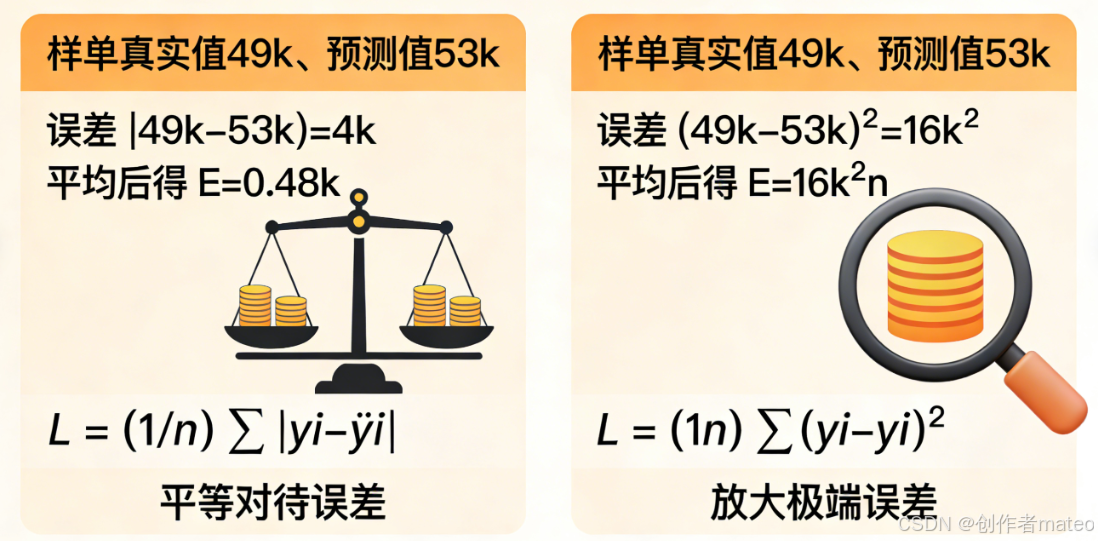
图注:两种常见的回归损失函数对比:平均绝对误差(MAE)对所有误差一视同仁,对异常值不敏感;均方误差(MSE)通过平方运算放大极端误差,更适合需要重点修正偏差的场景。
损失函数是关于参数的函数L(b,w)L(b, w)L(b,w),用于衡量模型预测值与真实值之间的差距。损失值越小,说明模型的预测效果越好,它是评估模型优劣的"标尺"。
2.1 常见的损失计算方式
- 平均绝对误差(MAE/Mean Absolute Error) :
- 计算公式:单样本误差e=∣y−y^∣e = |y - \hat{y}|e=∣y−y^∣(yyy为真实值,y^\hat{y}y^为模型预测值),整体损失为所有训练样本的平均误差,即L=1n∑i=1n∣yi−y^i∣L = \frac{1}{n}\sum_{i=1}^n |y_i - \hat{y}_i|L=n1∑i=1n∣yi−y^i∣(nnn为样本数量)。
- 特点 :对所有误差一视同仁,对异常值(outliers)不敏感。即便个别样本的预测误差很大,MAE也不会过度放大其影响。
- 均方误差(MSE/Mean Squared Error) :
- 计算公式:单样本误差e=(y−y^)2e = (y - \hat{y})^2e=(y−y^)2,整体损失为L=1n∑i=1n(yi−y^i)2L = \frac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2L=n1∑i=1n(yi−y^i)2。
- 特点 :通过平方运算放大了大误差的影响,对异常值敏感,能让模型更关注极端预测偏差的修正。
- 交叉熵(Cross-Entropy) :
- 适用场景:当yyy和y^\hat{y}y^为**概率分布(probability distributions)**时(比如分类任务中模型输出的类别概率),用交叉熵衡量两个分布的相似度。
- 作用:交叉熵值越小,代表预测分布与真实分布越契合,常作为分类任务的损失函数。
2.2 实际计算示例
以2017/01/01 - 2020/12/31的网页点击数据为训练集,代入暂定模型y=0.5k+1xy = 0.5k + 1xy=0.5k+1x计算:
- 2017/01/02的真实点击量为49k,模型预测值为53k,单样本MAE误差为∣49k−53k∣=4k|49k - 53k| = 4k∣49k−53k∣=4k,MSE误差为(49k−53k)2=16k2(49k - 53k)^2 = 16k^2(49k−53k)2=16k2;
- 计算训练集中每一天的误差后取平均值,得到模型在训练数据上的整体损失,以此判断当前参数bbb和www的拟合效果。
Step 3:模型优化(Optimization)
(配图4:梯度下降参数迭代示意图)
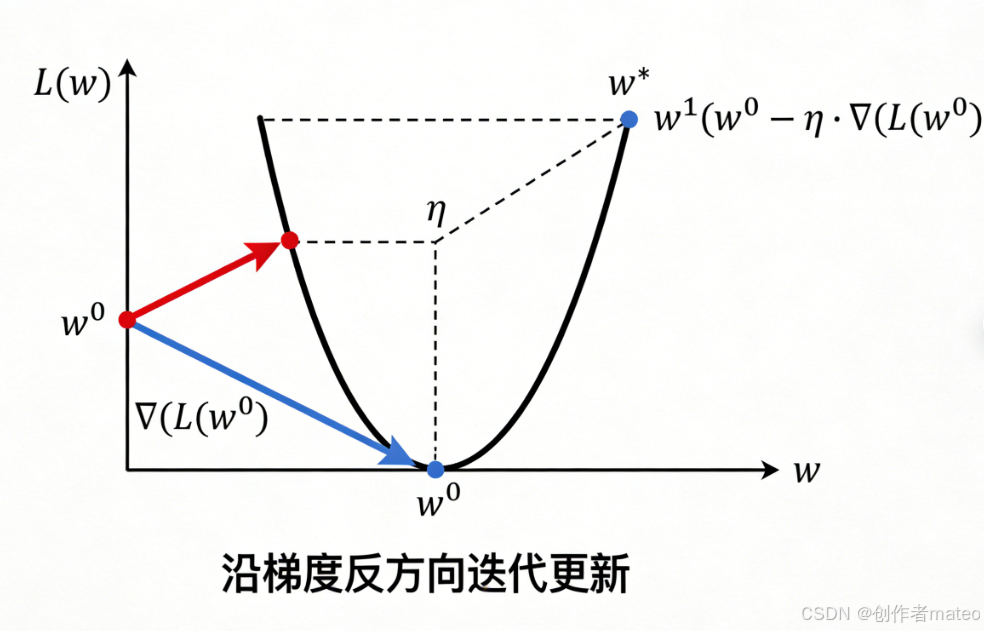
图注:梯度下降的核心逻辑是「沿着损失函数下降最快的方向更新参数」。图中曲线为损失函数 L(w)L(w)L(w),箭头方向代表参数 www 的更新路径,学习率 η\etaη 控制每次迭代的步长,最终收敛至损失最小的最优参数点。
优化的目标是找到能让损失函数最小化的最优参数w∗,b∗w^*, b^*w∗,b∗,数学表达为w∗,b∗=argminw,bL(b,w)w^*, b^* = \arg\min_{w,b} L(b, w)w∗,b∗=argminw,bL(b,w)。**梯度下降(Gradient Descent)**是机器学习中最常用的优化算法。
3.1 单参数的梯度下降流程
- 随机初始化 :为参数www随机选取一个初始值w0w^0w0(即优化的起点)。
- 计算梯度 :求解损失函数在w0w^0w0处的梯度dLdw∣w=w0\frac{dL}{dw}\big|_{w=w^0}dwdL w=w0,梯度代表损失函数上升最快的方向。
- 若梯度为负 :说明www增大时损失会减小,需增大www;
- 若梯度为正 :说明www减小时损失会减小,需减小www。
- 迭代更新 :用公式w′←w0−η⋅dLdw∣w=w0w' \leftarrow w^0 - \eta \cdot \frac{dL}{dw}\big|_{w=w^0}w′←w0−η⋅dwdL w=w0更新参数,其中η\etaη是学习率(learning rate) ,属于超参数,控制每次更新的步长(η\etaη过大易导致损失震荡不收敛,过小则训练速度过慢)。
3.2 超参数(Hyperparameters)
- 学习率η\etaη:需要手动设定,是影响梯度下降效率的关键超参数。
- 停止条件:当损失值收敛(损失变化量小于预设阈值)、梯度趋近于0,或达到预设的迭代次数时,停止参数更新。
3.3 多参数的梯度下降
对于线性模型y=b+wxy = b + wxy=b+wx中的www和bbb两个参数,优化步骤如下:
- 随机初始化参数的初始值w0w^0w0和b0b^0b0;
- 分别计算损失函数对www和bbb的偏导数:∂L∂w∣w=w0,b=b0\frac{\partial L}{\partial w}\big|{w=w^0, b=b^0}∂w∂L w=w0,b=b0和∂L∂b∣w=w0,b=b0\frac{\partial L}{\partial b}\big|{w=w^0, b=b^0}∂b∂L w=w0,b=b0;
- 同步更新参数:
w′←w0−η⋅∂L∂ww' \leftarrow w^0 - \eta \cdot \frac{\partial L}{\partial w}w′←w0−η⋅∂w∂L
b′←b0−η⋅∂L∂bb' \leftarrow b^0 - \eta \cdot \frac{\partial L}{\partial b}b′←b0−η⋅∂b∂L - 实操技巧:在TensorFlow、PyTorch等深度学习框架中,只需一行代码就能实现参数的自动迭代更新,无需手动计算梯度。
三、模型的训练与泛化能力
(配图5:模型训练集与测试集损失对比柱状图)
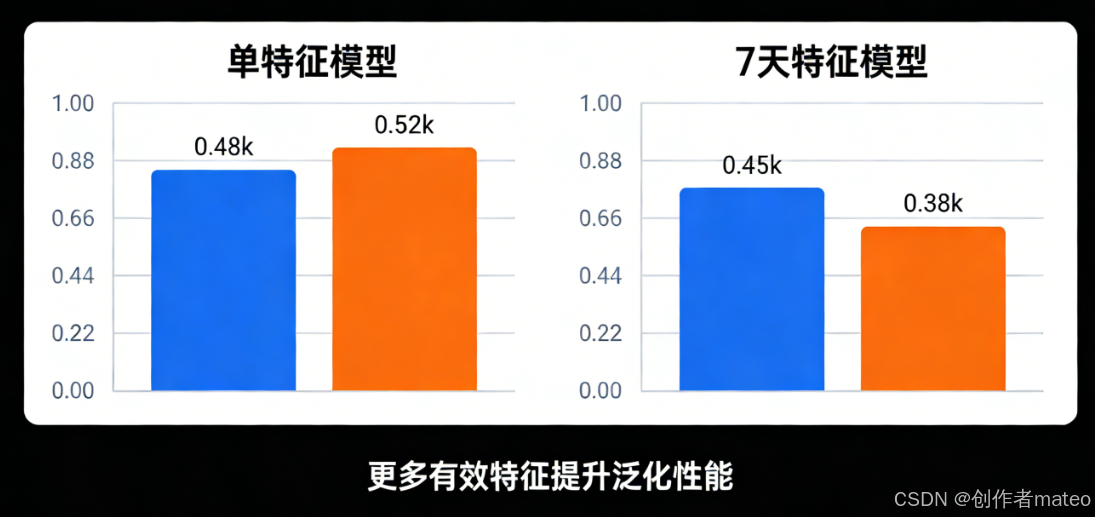
图注:模型泛化能力的提升案例:仅用昨日点击量作为特征的模型,在测试集上损失较高;引入过去7天点击量特征后,测试集损失从0.48k降至0.38k,泛化能力显著增强------更多有效特征有助于提升模型的泛化性能。
- 训练效果 :以模型y=0.1k+0.97xy = 0.1k + 0.97xy=0.1k+0.97x为例,在2017 - 2020年的训练数据上,该模型达到了L=0.48kL=0.48kL=0.48k的最小损失,说明在训练集上拟合效果较好。
- 泛化测试:用2021年未参与训练的新数据测试时,发现模型预测效果下降,这是因为模型对训练集过拟合,泛化能力不足。
- 优化泛化的尝试 :引入"过去7天的点击量"作为特征,将模型调整为y=b+17∑i=17wixiy = b + \frac{1}{7}\sum_{i=1}^7 w_i x_iy=b+71∑i=17wixi,此时模型在测试集上的损失降至L=0.38kL=0.38kL=0.38k,泛化能力得到提升。
四、从线性模型到非线性模型的演进
4.1 线性模型的局限性
线性模型y=wx+by = wx + by=wx+b的输出始终是一条直线,只能拟合线性关系,无法处理正相关、负相关交替的非线性关系,存在模型偏差(Model Bias)。如果一直使用线性模型,永远无法拟合复杂的曲线关系,因此需要引入更灵活的模型。
4.2 分段线性近似(Piecewise Linear Curves)
- 核心思路:用多段直线拼接的方式近似拟合曲线,分段数量越多,能拟合的曲线就越复杂。
- 原理:基于微分思想,只要分段足够密集,分段线性曲线就能无限逼近连续的非线性曲线。
- 典型示例:Hard Sigmoid(硬Sigmoid)是典型的分段线性函数,常作为非线性拟合的基础单元。
4.3 非线性激活函数:Sigmoid
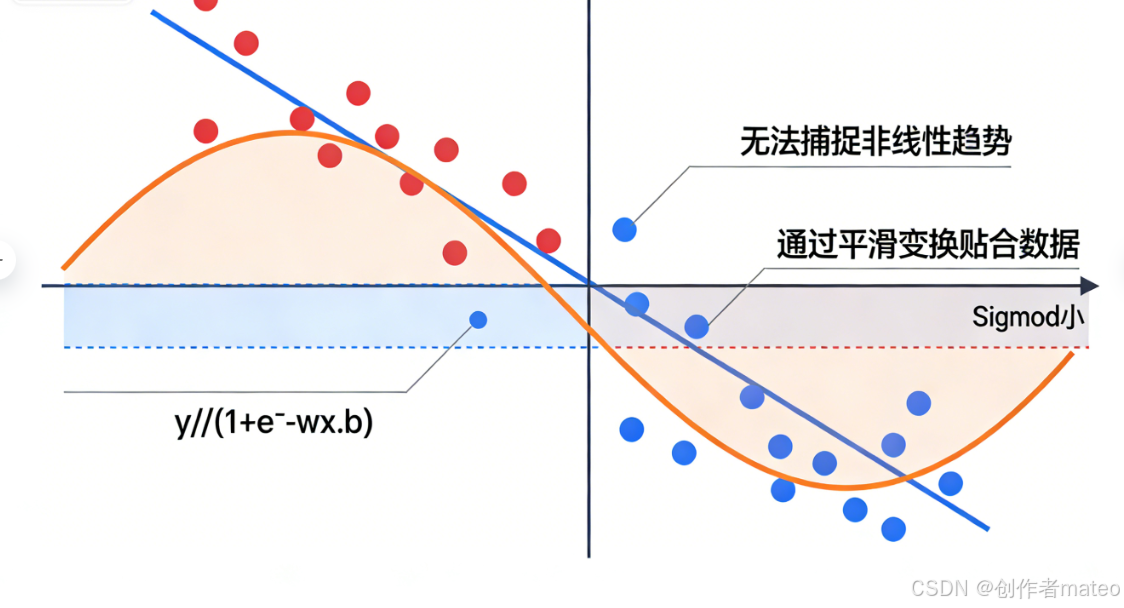
(配图6:线性模型与非线性模型拟合效果对比图)
图注:线性模型的局限性与非线性模型的优势:直线无法拟合复杂的非线性数据分布,而Sigmoid曲线通过平滑的非线性变换,能更精准地贴合数据趋势,是解决非线性问题的基础工具。
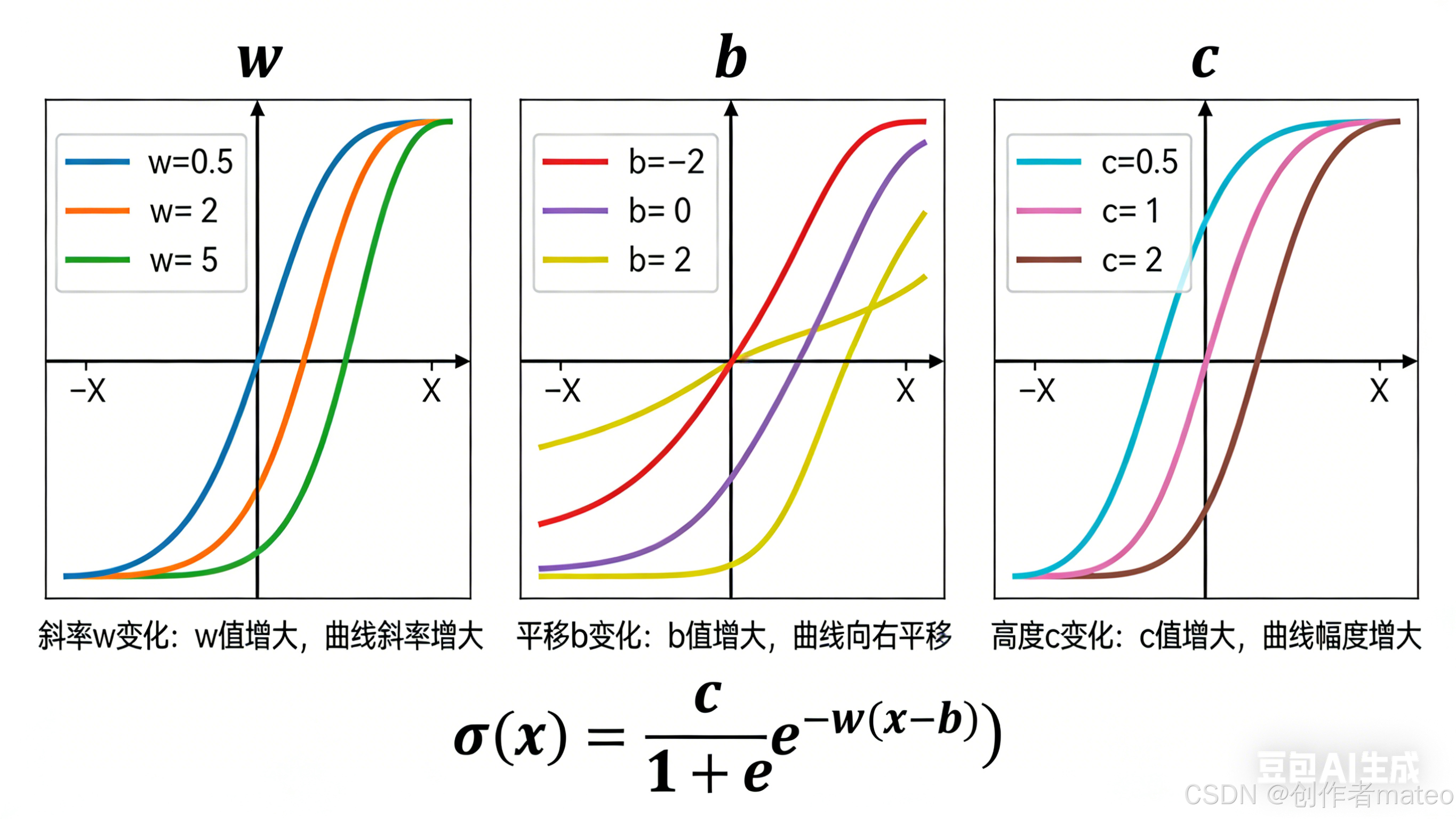
(配图7:Sigmoid函数参数影响示意图)
图注:Sigmoid函数 y=c⋅11+e−(wx+b)y = c \cdot \frac{1}{1+e^{-(wx+b)}}y=c⋅1+e−(wx+b)1 的参数调控效果:www 决定曲线的陡峭程度,bbb 控制曲线的左右平移,ccc 调整曲线的上下高度,三者配合可拟合不同形态的非线性关系。
为了实现更平滑的非线性拟合,引入Sigmoid函数,其公式为:
y=c⋅11+e−(wx+b)y = c \cdot \frac{1}{1 + e^{-(wx + b)}}y=c⋅1+e−(wx+b)1
- 参数的作用 :
- www:改变曲线的斜率(slope);
- bbb:让曲线发生平移(shift);
- ccc:调整曲线的高度(height)。
- 优势:和分段线性函数相比,Sigmoid是连续平滑的非线性函数,能更好地拟合复杂的非线性关系,也是神经网络中常用的激活函数之一。
五、多特征非线性模型的构建
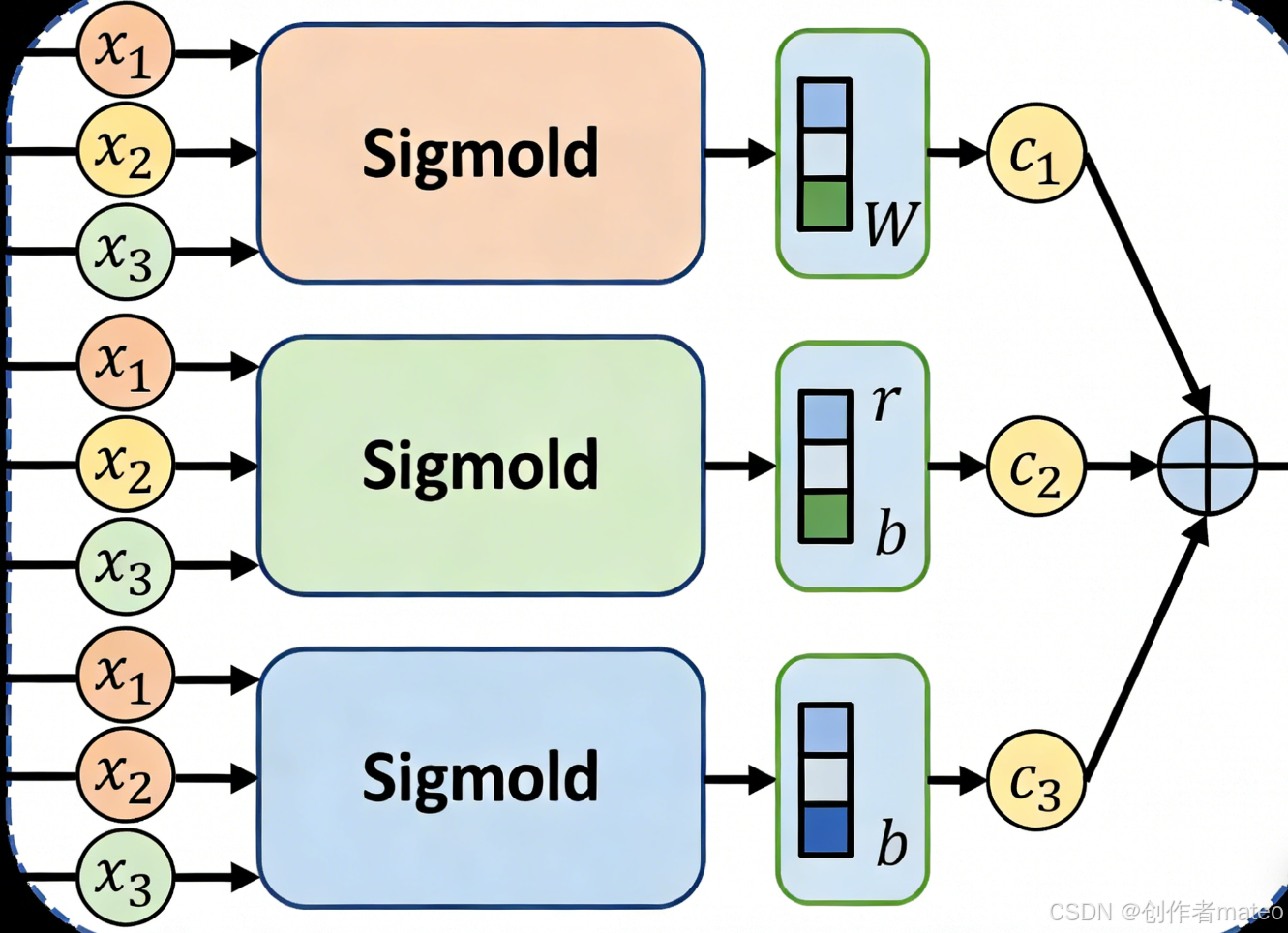
(配图8:多Sigmoid组合的非线性模型结构图)
图注:多Sigmoid组合模型的结构:输入层为多个特征(如前3天点击量),中间层为3个Sigmoid单元(分别拟合局部非线性特征),输出层将Sigmoid的结果线性组合,最终得到预测值。
当单一特征无法满足拟合需求时,需引入多特征(More Features) 并结合非线性激活函数,构建更复杂的模型以拟合高维、非线性的数据关系。
5.1 多Sigmoid组合的非线性模型
- 核心公式 :将多个Sigmoid函数线性组合,形成能拟合复杂曲线的模型,公式为:
y=b+∑ici⋅sigmoid(bi+∑jwijxj)y = b + \sum_{i} c_i \cdot \text{sigmoid}(b_i + \sum_{j} w_{ij} x_j)y=b+i∑ci⋅sigmoid(bi+j∑wijxj)
其中iii代表第iii个Sigmoid单元,jjj代表第jjj个输入特征。 - 参数含义 :
- xjx_jxj:第jjj个输入特征(如网页点击预测中,x1x_1x1为前1天点击量,x2x_2x2为前2天点击量,x3x_3x3为前3天点击量);
- wijw_{ij}wij:第iii个Sigmoid单元对应第jjj个特征的权重(Weight for xjx_jxj for iii-th sigmoid);
- bib_ibi:第iii个Sigmoid单元的偏置项;
- cic_ici:第iii个Sigmoid单元输出的权重系数。
- 模型意义:每个Sigmoid单元负责拟合数据的一个局部非线性特征,通过线性组合多个Sigmoid的输出,实现对整体复杂非线性关系的拟合。
5.2 模型的矩阵向量化表示
(配图9:多Sigmoid输入的矩阵运算示意图)
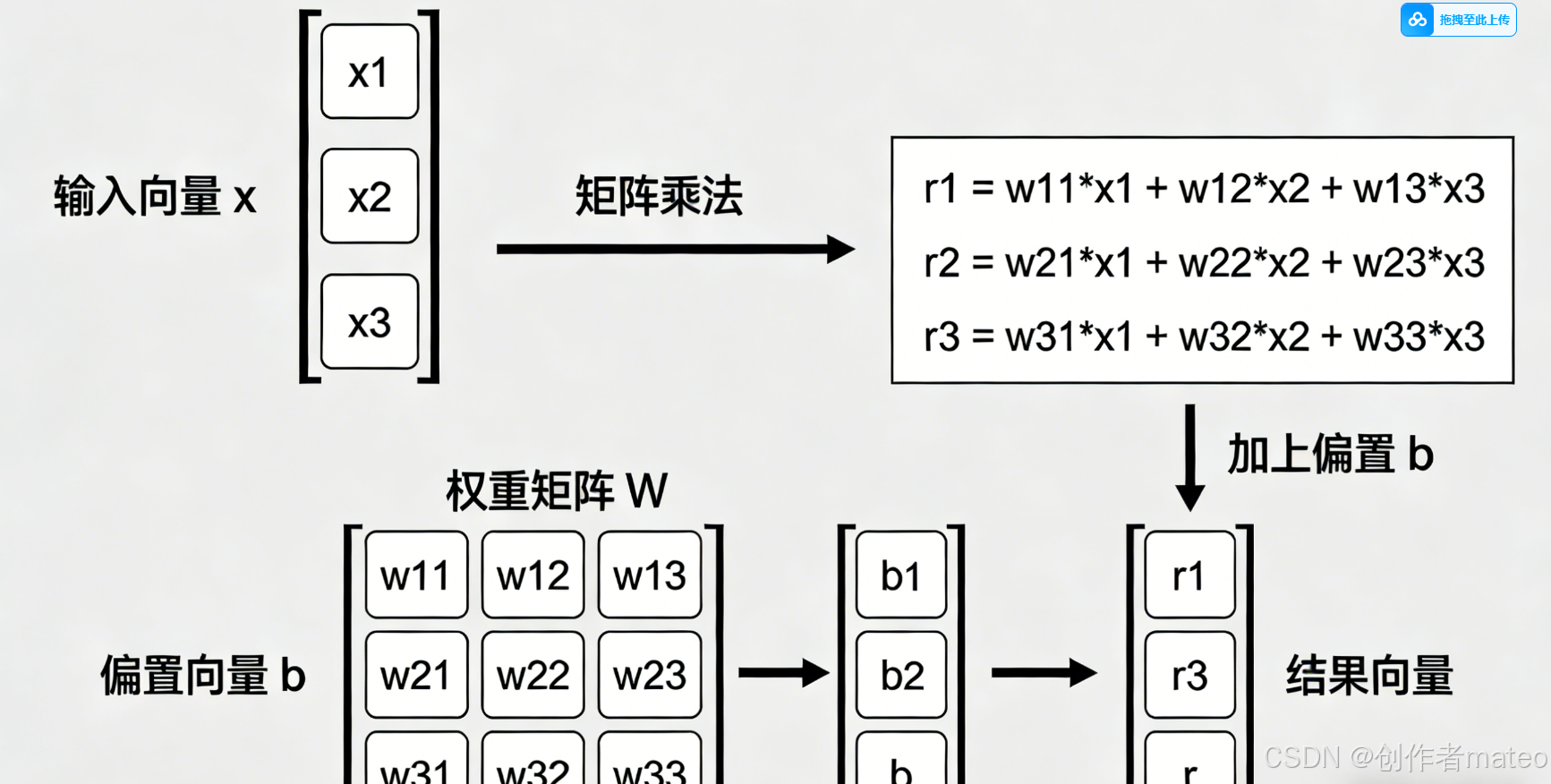
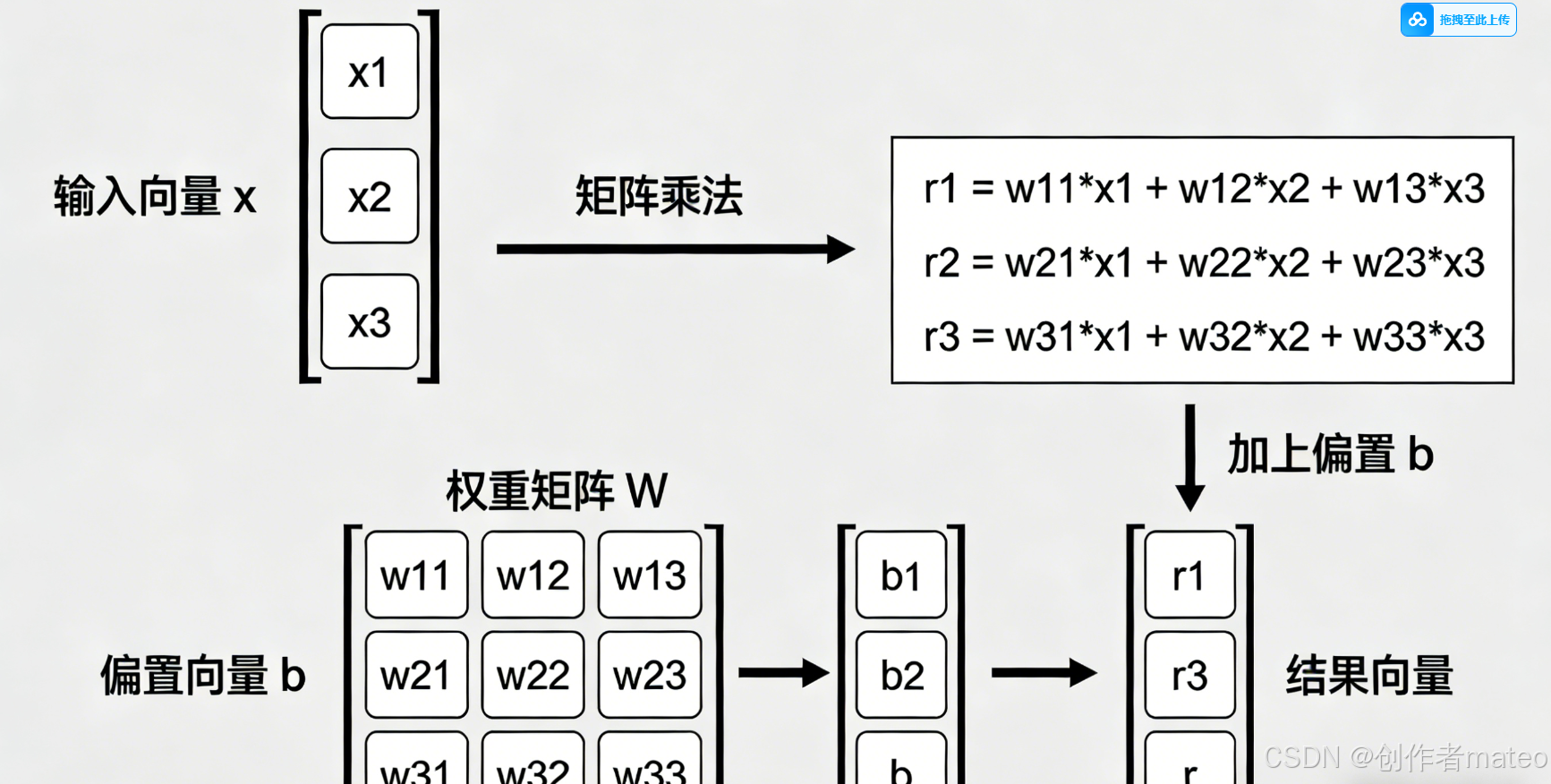
图注:多Sigmoid输入的矩阵向量化转换:将3个Sigmoid单元的输入计算(ri=bi+wi1x1+wi2x2+wi3x3r_i = b_i + w_{i1}x_1 + w_{i2}x_2 + w_{i3}x_3ri=bi+wi1x1+wi2x2+wi3x3)整合为矩阵乘法 r⃗=b⃗+W⋅x⃗\vec{r} = \vec{b} + W \cdot \vec{x}r =b +W⋅x ,大幅提升计算效率。
为了简化计算并适配计算机的矩阵运算能力,将多Sigmoid的输入部分转化为矩阵与向量的乘法形式:
- 定义输入向量与参数矩阵 :
- 输入特征向量:x⃗=[x1x2x3]\vec{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}x = x1x2x3
- 偏置向量:b⃗=[b1b2b3]\vec{b} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix}b = b1b2b3
- 权重矩阵:W=[w11w12w13w21w22w23w31w32w33]W = \begin{bmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ w_{31} & w_{32} & w_{33} \end{bmatrix}W= w11w21w31w12w22w32w13w23w33
- 矩阵形式的输入计算 :
每个Sigmoid单元的输入ri=bi+∑jwijxjr_i = b_i + \sum_{j} w_{ij} x_jri=bi+∑jwijxj,整合为矩阵运算:
r⃗=b⃗+W⋅x⃗\vec{r} = \vec{b} + W \cdot \vec{x}r =b +W⋅x
其中r⃗=[r1r2r3]\vec{r} = \begin{bmatrix} r_1 \\ r_2 \\ r_3 \end{bmatrix}r = r1r2r3 ,代表三个Sigmoid单元的输入向量。 - 优势:矩阵运算能大幅提升计算效率,尤其是在特征数和Sigmoid单元数较多时,可借助GPU实现并行计算。
六、模型优化的工程实现:批量梯度下降
(配图10:批量梯度下降流程图)
图注:批量梯度下降的工程流程:将总样本按Batch Size分块,每次用一个Batch计算梯度并更新参数,遍历所有Batch完成1个Epoch,重复训练直至模型收敛。该策略平衡了计算效率与优化精度。
前文的梯度下降为全量梯度下降(Full Batch Gradient Descent) ,在实际工程中,由于数据量庞大,全量计算梯度会导致效率极低,因此引入批量(Batch) 与小批量(Mini-Batch) 梯度下降策略。
6.1 核心概念定义
- 样本总量(NNN) :训练集的总样本数(如示例中N=10,000N=10,000N=10,000);
- 批量大小(Batch Size, BBB) :每次参与梯度计算的样本数(如示例中B=10B=10B=10);
- 迭代(Update):用一个Batch的样本计算梯度并更新一次参数,称为一次迭代;
- 轮次(Epoch):将所有训练样本完整遍历一次(即所有Batch都参与计算),称为一个Epoch。
6.2 批量梯度下降的计算流程
- 参数初始化 :随机选取模型参数的初始值θ0\theta^0θ0(θ\thetaθ包含所有权重和偏置,如WWW、b⃗\vec{b}b 、cic_ici等);
- 数据分批次 :将总样本数NNN按Batch Size BBB划分为若干个Batch(示例中N=10,000N=10,000N=10,000,B=10B=10B=10,共1000个Batch);
- 迭代更新参数 :
- 对每个Batch,计算该批次样本的损失LLL和梯度∇L(θ)\nabla L(\theta)∇L(θ);
- 按梯度下降公式更新参数:θ′←θ−η⋅∇L(θ)\theta' \leftarrow \theta - \eta \cdot \nabla L(\theta)θ′←θ−η⋅∇L(θ)(η\etaη为学习率);
- 轮次循环:重复步骤2-3,直到遍历完所有Batch(完成1个Epoch),通常会训练多个Epoch直至模型收敛。
6.3 批量策略的作用
- 数据分块:避免因样本量过大导致的内存溢出问题,实现大数据集的分批处理;
- 梯度近似:用Mini-Batch的梯度近似全量数据的梯度,在保证优化方向准确的前提下,大幅提升训练速度;
- 收敛特性:Mini-Batch梯度下降的损失曲线会围绕最优值震荡,但收敛速度远快于全量梯度下降,是深度学习中最常用的优化策略。
6.4 迭代停止条件的工程考量
在实际训练中,很难等到梯度完全为0时停止迭代,通常采用以下停止条件:
- 损失收敛 :连续多个Epoch的损失变化量小于预设阈值(如10−610^{-6}10−6);
- 达到最大迭代次数:预设最大Epoch数(如100),防止模型过拟合或无意义的长时间训练;
- 验证集指标下降:当验证集的损失或准确率不再提升时,提前停止训练(早停,Early Stopping)。