残差连接(Residual Connection)的数学原理核心是通过残差映射和恒等映射的结合,解决深度神经网络训练中的梯度消失问题。其本质是将传统的网络层学习任务从直接拟合目标函数 H(x)H(x)H(x) 转变为学习残差 F(x)=H(x)−xF(x)=H(x)-xF(x)=H(x)−x,从而保证梯度在深层网络中能够有效传播。
1.基本数学表达
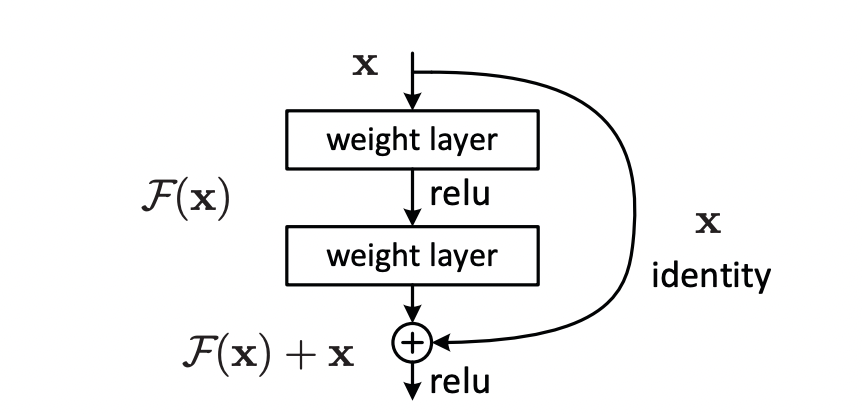
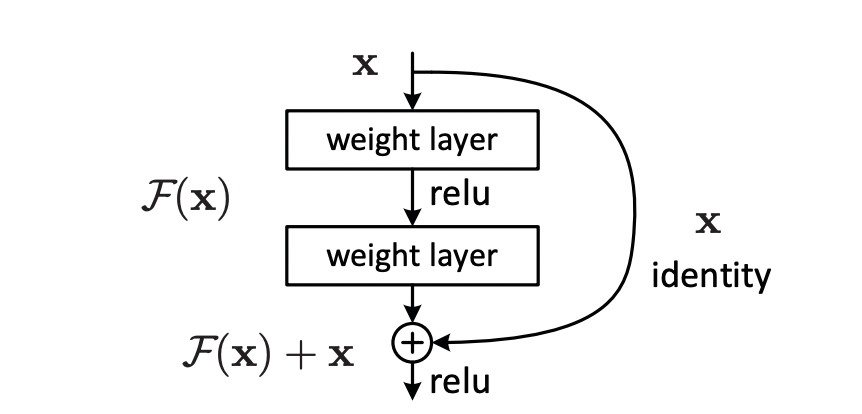
残差连接的基本形式为:y=F(x)+xy=F(x)+xy=F(x)+x,其中:
- xxx 是当前层的输入
- F(x)F(x)F(x) 是当前层子网络(如卷积层、全连接层等)学习的残差函数
- yyy 是当前层的输出
关键洞察 :传统网络要求子网络直接学习完整的映射 H(x)H(x)H(x),而残差网络只需学习输入与输出的差异 F(x)=H(x)−xF(x)=H(x)-xF(x)=H(x)−x。当子网络未学到有效特征时,F(x)F(x)F(x) 可以近似为0,此时 y≈xy\approx xy≈x,即网络退化为恒等映射,保证模型性能不会因深度增加而下降。
2.梯度传播的数学分析
残差连接的核心优势在于梯度的稳定传播 。假设损失函数为 L\mathcal{L}L,对输出 yyy 的梯度为 ∂L∂y\frac{\partial \mathcal{L}}{\partial y}∂y∂L,则根据链式法则,对输入 xxx 的梯度为:
∂L∂x=∂L∂y⋅∂y∂x=∂L∂y(∂F(x)∂x+1)\frac{\partial \mathcal{L}}{\partial x} = \frac{\partial \mathcal{L}}{\partial y}\cdot \frac{\partial y}{\partial x} = \frac{\partial \mathcal{L}}{\partial y}\left(\frac{\partial F(x)}{\partial x}+1\right) ∂x∂L=∂y∂L⋅∂x∂y=∂y∂L(∂x∂F(x)+1)
梯度保护机制:
当子网络的梯度 ∂F(x)∂x\frac{\partial F(x)}{\partial x}∂x∂F(x) 趋近于0时,总梯度 ∂L∂x≈∂L∂y\frac{\partial \mathcal{L}}{\partial x}\approx \frac{\partial \mathcal{L}}{\partial y}∂x∂L≈∂y∂L,避免了梯度消失。
即使子网络的梯度为负(如∂F(x)∂x=−0.5\frac{\partial F(x)}{\partial x}=-0.5∂x∂F(x)=−0.5),总梯度仍为0.5,不会完全消失。
3.深层网络的递归展开
对于包含n个残差块的深层网络,其输出可递归展开为:
yn=x+F1(x)+F2(y1)+⋯+Fn(yn−1)y_n=x+F_1(x)+F_2(y_1)+\cdots+F_n(y_{n-1})yn=x+F1(x)+F2(y1)+⋯+Fn(yn−1)
其中 yi=x+∑k=1iFk(yk−1)y_i=x+\sum_{k=1}^iF_k(y_{k-1})yi=x+∑k=1iFk(yk−1),y0=xy_0=xy0=x
展开后的特性:
- 每一层的输出都包含初始输入的直接贡献,打破了传统网络的链式依赖。
- 反向传播时,梯度可以通过所有残差块的恒等映射路径直接传递到输入层,如:
∂L∂x=∂L∂yn+∑i=1n∂L∂yn ∏k=i+1n∂Fk∂yk−1\frac{\partial \mathcal{L}}{\partial x} = \frac{\partial \mathcal{L}}{\partial y_n}+ \sum_{i=1}^{n} \frac{\partial \mathcal{L}}{\partial y_n}\, \prod_{k=i+1}^{n} \frac{\partial F_k}{\partial y_{k-1}} ∂x∂L=∂yn∂L+i=1∑n∂yn∂Lk=i+1∏n∂yk−1∂Fk
其中第一项 ∂L∂yn\frac{\partial \mathcal{L}}{\partial y_n}∂yn∂L 是通过恒等映射直接传递的梯度,后续项是通过子网络传递的梯度。
4.恒等映射的重要性
残差连接的有效性依赖于恒等映射的严格满足。若子网络的输出维度与输入维度不一致(如通道数变化),则需要引入投影矩阵 WWW 进行维度匹配:y=F(x)+Wxy=F(x)+Wxy=F(x)+Wx 但研究表明,直接恒等映射 (W=I)(W=I)(W=I) 的效果最优。当使
用投影矩阵时,模型性能会略有下降,因为投影操作破坏了原始输入的直接传递。
5.与传统网络的对比
| 特性 | 传统网络 | 残差网络 |
|---|---|---|
| 学习目标 | 直接拟合 H(x)H(x)H(x) | 拟合残差 F(x)=H(x)−xF(x)=H(x)-xF(x)=H(x)−x |
| 梯度传播 | 链式乘积,易消失(如0.9100≈00.9^{100}\approx 00.9100≈0) | 包含恒等项,梯度稳定(如0.9+1=1.9) |
| 网络深度 | 通常不超过20层 | 可轻松扩展到1000层以上 |
| 性能退化 | 深度增加时性能下降 | 深度增加时性能稳步提升 |
总结
残差连接的数学原理可概括为:
- 残差映射:将学习任务简化为拟合输入与输出的差异,降低学习难度。
- 恒等映射:通过直接传递输入,保证梯度在深层网络中不消失。
- 递归展开:深层网络的输出是所有残差块的叠加,保留了各层的特征贡献。
这种简洁而深刻的设计,使得残差网络成为深度学习领域
的基石,广泛应用于图像识别(ResNet)、自然语言处
理(Transformer)等任务中。