卡尔曼滤波 | UKF 原理、仿真与实现

斐夷所非2026-01-11 8:31

注：本文为 "卡尔曼滤波 " 相关合辑。

图片清晰度受引文原图所限。

略作重排，未整理去重。

如有内容异常，请看原文。

无迹卡尔曼滤波-1

posted @ 2016-03-02 14:35 XXX已失联

1 引言与无迹变换定义

无迹卡尔曼滤波 (Unscented Kalman Filter, UKF) 的理论基础为无迹变换。维基百科对无迹变换 (Unscented Transform, UT) 的定义如下：

The unscented transform (UT) is a mathematical function used to estimate the result of applying a given nonlinear transformation to a probability distribution that is characterized only in terms of a finite set of statistics. The most common use of the unscented transform is in the nonlinear projection of mean and covariance estimates in the context of nonlinear extensions of the Kalman filter.

2 非线性映射下的统计量求解问题

为理解无迹变换的思想，首先分析如下基础问题：设 X X X 为服从正态分布的一维随机变量， Y Y Y 为随机变量 X X X 经非线性映射得到的随机变量，求解随机变量 Y Y Y 的数学期望与方差。
X ∼ N ( μ , σ 2 ) , Y = sin ⁡ ( X ) X \sim \mathcal{N}(\mu, \sigma^2) , \quad Y = \sin(X) X∼N(μ,σ2),Y=sin(X)

2.1 理论求解方法

根据数理统计的基础理论，若连续型随机变量 X X X 的概率密度函数为 f ( x ) f(x) f(x)，则随机变量 Y = g ( X ) Y=g(X) Y=g(X) 的数学期望定义为：

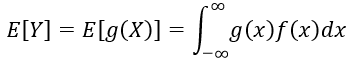
求解该数学期望需计算反常积分，也可先推导 Y Y Y 的分布函数，求导得到其概率密度函数后，再依据数学期望的定义完成求解。

方差的计算公式如下，可见方差的求解需以数学期望的计算结果为前提：

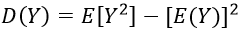
2.2 一阶泰勒展开近似解法

实际求解中，反常积分存在求解难度大或积分不收敛的情况，将导致该方法的可行性降低。对此可采用近似解法：将函数 y = sin ⁡ ( x ) y=\sin(x) y=sin(x) 在 x = μ x=\mu x=μ 处做一阶泰勒展开并忽略高阶小项，展开形式为：

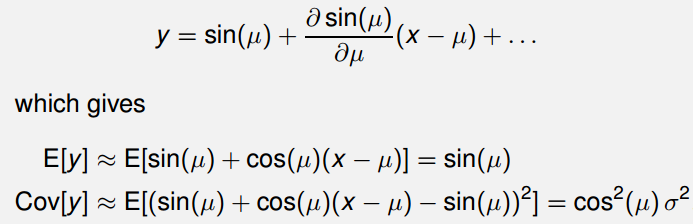
3 泰勒展开近似的数值验证与误差分析

3.1 数值实验实现

该近似方法的计算精度可通过数值实验进行验证，实验代码如下：

python 复制代码 
from numpy import sin,cos,exp,inf,pi
import scipy.integrate as integrate

mu = 1      # 期望
sigma = 1   # 标准差

# Y = sin(X)
# 按公式计算E[Y]和D[Y]
f1 = lambda x:  sin(x) * exp(-(x-mu)**2/(2*sigma**2)) / ((2*pi)**0.5*sigma)
f2 = lambda x:  sin(x)**2 * exp(-(x-mu)**2/(2*sigma**2)) / ((2*pi)**0.5*sigma)
f_mu, err = integrate.quad( f1,  -inf,  inf)
temp, err = integrate.quad( f2,  -inf,  inf)
f_cov = temp - f_mu**2

print(f_mu, f_cov)

# 按一阶泰勒展开近似计算
print(sin(mu), cos(mu)**2 * sigma**2)

3.2 实验结果与误差分析

数值实验得到的数学期望与方差计算结果如下：
0.510377951545 0.267674021573 0.510377951545 \quad 0.267674021573 0.5103779515450.267674021573
0.841470984808 0.291926581726 0.841470984808 \quad 0.291926581726 0.8414709848080.291926581726

第一行数据为基于公式的数值积分精确解，第二行数据为一阶泰勒展开的近似解。对比可知，一阶泰勒展开的计算结果与理论值之间存在显著误差。一阶泰勒展开的本质是在局部区域用线性函数逼近非线性函数，这意味着当函数呈现强非线性特征时，一阶泰勒展开的近似误差会显著增大。

该规律可通过如下案例佐证：对于函数 f ( x ) = sin ⁡ x f(x)=\sin x f(x)=sinx 与 g ( x ) = sin ⁡ 2 x g(x)=\sin2x g(x)=sin2x，在 x = π / 4 x=\pi/4 x=π/4 处，函数 g ( x ) g(x) g(x) 的非线性程度显著高于 f ( x ) f(x) f(x)；对两个函数在该位置做一阶泰勒展开，分别求解随机变量 Y = sin ⁡ ( X ) Y=\sin(X) Y=sin(X) 与 Y = sin ⁡ ( 2 X ) Y=\sin(2X) Y=sin(2X) 的数学期望，可得 g ( x ) g(x) g(x) 对应的期望绝对误差大于 f ( x ) f(x) f(x)。

4 泰勒展开近似法的局限性与EKF的缺陷

综上，非线性问题的一阶泰勒展开近似法存在诸多局限性：高阶项不可忽略时将产生较大的截断误差；部分非线性函数的求导过程复杂；计算精度与函数的非线性程度强相关。针对此类问题，亟需一种无需泰勒展开、且能保证计算精度的求解方法。

扩展卡尔曼滤波 (Extended Kalman Filter, EKF) 同样采用一阶泰勒展开结合雅可比矩阵完成非线性系统的线性化近似，因此上述局限性同样存在于 EKF 算法中。本文将基于该问题逐步推导无迹卡尔曼滤波 (UKF) 的原理，并完成其与 EKF 算法的特性对比。

参考

https://en.wikipedia.org/wiki/Unscented_transform
http://www.lce.hut.fi/~ssarkka/course_k2010/slides_5.pdf

无迹卡尔曼滤波-2

posted @ 2016-03-02 19:16 XXX已失

1 采样法的思路与维度爆炸问题

针对前文提出的问题 X ∼ N ( μ , σ 2 ) , Y = sin ⁡ ( X ) X \sim \mathcal{N}(\mu, \sigma^2) , \ Y = \sin(X) X∼N(μ,σ2), Y=sin(X)，求解随机变量 Y Y Y 的数学期望与方差，可提出另一类求解思路：对随机变量 X X X 进行采样得到样本点（该类样本点被定义为 σ \sigma σ 点），再基于采样点的统计特征求解期望与方差。当采样点数量足够大时，统计结果将逼近理论值。

该思路存在明显的缺陷：随着随机变量维度的提升，所需采样点的数量会呈指数级增长。例如，一维随机变量需 500 500 500 个采样点，二维随机变量则需要 500 2 = 250000 500^2=250000 5002=250000 个采样点，三维随机变量需要 500 3 = 125000000 500^3=125000000 5003=125000000 个采样点，将造成巨大的计算开销。

无迹卡尔曼滤波算法提出了一种高效的采样策略：对 n n n 维随机变量仅选取 2 n + 1 2n+1 2n+1 个 σ \sigma σ 点即可完成统计特征的高精度近似，从根本上解决了维度爆炸带来的计算负担问题。

2 一维随机变量的σ点采样规则

如上图所示，利用正态分布的对称性，对一维随机变量选取 3 3 3 个 σ \sigma σ 点即可完成近似计算（ σ \sigma σ 点的选取方式不唯一），其中 1 1 1 个采样点为均值点，另外 2 2 2 个采样点关于均值对称分布，选取形式如下：
χ 0 = μ ; χ 1 = μ + σ ; χ 2 = μ − σ ; \begin{align*} \chi_0 &= \mu; \\ \chi_1 &= \mu + \sigma; \\ \chi_2 &= \mu - \sigma; \end{align*} χ0χ1χ2=μ;=μ+σ;=μ−σ;

2.1 权值的约束关系

为保证采样点的统计特性与原分布一致，为每个 σ \sigma σ 点分配对应的权值 W i W_i Wi，权值需满足如下约束关系：

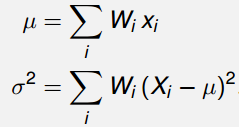
2.2 数字特征的近似求解

基于上述采样点与权值，可通过如下公式近似求解 Y = sin ⁡ ( X ) Y=\sin(X) Y=sin(X) 的数字特征：

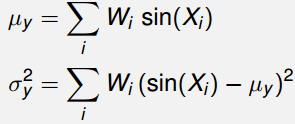
3 多维随机变量的无迹变换推广

将该方法推广至多维场景：设 n n n 维随机向量 X ∼ N ( μ , Σ ) \boldsymbol{X} \sim \mathcal{N}(\boldsymbol{\mu},\boldsymbol{\Sigma}) X∼N(μ,Σ)，其中 Σ \boldsymbol{\Sigma} Σ 为随机向量 X \boldsymbol{X} X 的协方差矩阵。对协方差矩阵做 Cholesky 分解可得下三角矩阵 L \boldsymbol{L} L，满足 Σ = L L T \boldsymbol{\Sigma} = \boldsymbol{L}\boldsymbol{L}^\mathrm{T} Σ=LLT，该矩阵 L \boldsymbol{L} L 可视为一维场景下标准差 σ \sigma σ 的多维推广形式。

3.1 多维σ点的选取形式

多维场景下的 σ \sigma σ 点选取形式为：
χ 0 = μ ; χ i = μ + c L ; χ n + i = μ − c L ; \begin{align*} \boldsymbol{\chi}_0 &= \boldsymbol{\mu}; \\ \boldsymbol{\chi}i &= \boldsymbol{\mu} + c\boldsymbol{L}; \\ \boldsymbol{\chi}{n+i} &= \boldsymbol{\mu} - c\boldsymbol{L}; \end{align*} χ0χiχn+i=μ;=μ+cL;=μ−cL;

式中， c c c 为正的常数。

3.2 多维非线性映射的统计量计算

对非线性变换 Y = g ( X ) \boldsymbol{Y}=\boldsymbol{g}(\boldsymbol{X}) Y=g(X)，变换后随机向量的数学期望与协方差可通过如下公式完成近似计算：

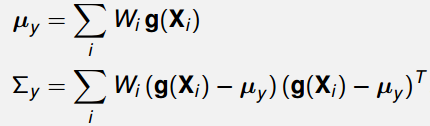
4 规范化的σ点与权值选取准则

该方法的要点为 σ \sigma σ 点与权值的规范化选取，主流的标准选取方式为：

  1. 首个 σ \sigma σ 点固定选取为均值，即 χ 0 = μ \boldsymbol{\chi}_0=\boldsymbol{\mu} χ0=μ；
  2. 设定常数 α , κ , λ \alpha, \kappa, \lambda α,κ,λ，三者满足如下关联公式：

其余 2 n 2n 2n 个 σ \sigma σ 点的计算公式如下，式中下标 i i i 表示矩阵 L \boldsymbol{L} L 的第 i i i 列：

4.1 权值的分配规则

完成 σ \sigma σ 点的选取后，对所有采样点分配对应的权值，均值权值与协方差权值的分配规则相互独立：

  • 求解数学期望时，首个 σ \sigma σ 点的权值为：
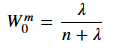
  • 求解协方差时，首个 σ \sigma σ 点的权值为（式中 β \beta β 为额外引入的常数）：
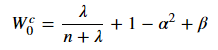
  • 剩余 2 n 2n 2n 个 σ \sigma σ 点的均值权值与协方差权值完全相同，其表达式为：

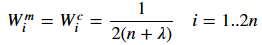
4.2 超参数的经验整定规则

综上，无迹变换中共需整定 α , β , κ \alpha, \beta, \kappa α,β,κ 三个超参数，相关学术研究给出的经验整定规则为：
β = 2 \beta=2 β=2 为高斯分布下的最优取值； κ = 3 − n \kappa=3-n κ=3−n 为适配维度的推荐取值； α \alpha α 的取值区间为 0 ≤ α ≤ 1 0 \le \alpha \le 1 0≤α≤1。

参数 α \alpha α 的物理意义为： α \alpha α 取值越大，均值处的 σ \sigma σ 点权重占比越高，其余采样点则越远离均值。

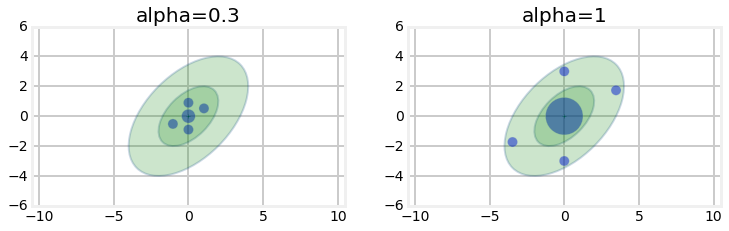
如上图所示，对 2 2 2 维随机变量选取 5 5 5 个 σ \sigma σ 点，图中点的大小表征对应权值的大小。由概率分布的特性可知，远离均值的采样点应分配更小的权值，符合该参数整定的内在逻辑。

5 无迹变换的Python实现

基于上述理论推导的计算流程与公式，可完成 σ \sigma σ 点选取与权值计算的程序化实现。在 Python 环境中，可直接调用开源库 FilterPy \textbf{FilterPy} FilterPy 完成相关计算，该库可通过 pip 工具完成安装，执行命令为 pip install filterpy。

python 复制代码 
# -*- coding: utf-8 -*-
from filterpy.kalman import MerweScaledSigmaPoints as SigmaPoints

mean = 0    # 均值
cov =  1    # 方差

points = SigmaPoints(n=1, alpha=0.1, beta=2.0, kappa=1.0)  
Wm, Wc = points.weights()
sigmas = points.sigma_points(mean, cov)

print(Wm, Wc)    # 计算均值和方差的权值
print(sigmas)    # sigma点的坐标

对标准正态分布执行上述代码，输出结果如下：

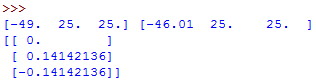
6 二维正态分布的无迹变换数值验证

选取服从二维正态分布的随机变量，其数学期望与协方差矩阵为：

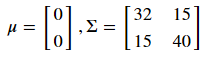
对该随机变量执行如下非线性变换：

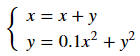
下文将通过无迹变换近似求解非线性变换后随机变量的数学期望，并与直接采样 1000 1000 1000 个样本点的统计结果进行对比，验证无迹变换的精度与效率优势。

python 复制代码 
# -*- coding: utf-8 -*-
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
from numpy.random import multivariate_normal
from filterpy.kalman import unscented_transform
from filterpy.kalman import MerweScaledSigmaPoints as SigmaPoints

# 非线性变换函数
def f_nonlinear_xy(x, y):
    return np.array([x + y, 0.1*x**2 + y**2])

def plot1(xs, ys):
    xs = np.asarray(xs) 
    ys = np.asarray(ys)
    xmin = xs.min()
    xmax = xs.max()
    ymin = ys.min()
    ymax = ys.max()
    values = np.vstack([xs, ys])  
    kernel = stats.gaussian_kde(values)   
    X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]
    positions = np.vstack([X.ravel(), Y.ravel()])
    Z = np.reshape(kernel.evaluate(positions).T, X.shape)  
    plt.imshow(np.rot90(Z),cmap=plt.cm.Greys,extent=[xmin, xmax, ymin, ymax])
    plt.plot(xs, ys, 'k.', markersize=2)
    plt.xlim(-20, 20)
    plt.ylim(-20, 20)
   
def plot2(xs, ys, f, mean_fx):
    fxs, fys = f(xs, ys)    # 将采样点进行非线性变换
    computed_mean_x = np.average(fxs)   
    computed_mean_y = np.average(fys)
    plt.subplot(121)
    plt.grid(False)
    plot1(xs, ys)
    plt.subplot(122)
    plt.grid(False)
    plot1(fxs, fys)
    plt.scatter(fxs, fys, marker='.', alpha=0.01, color='k')
    plt.scatter(mean_fx[0], mean_fx[1], marker='o', s=100, c='r', label='UT_mean')
    plt.scatter(computed_mean_x, computed_mean_y, marker='*',s=120, c='b', label='mean')
    plt.ylim([-10, 200])
    plt.xlim([-100, 100])
    plt.legend(loc='best', scatterpoints=1)
    print ('Difference in mean x={:.3f}, y={:.3f}'.format(
           computed_mean_x-mean_fx[0], computed_mean_y-mean_fx[1]))
    
# -------------------------------------------------------------------------------------------
mean = [0, 0]               # Mean of the N-dimensional distribution.
cov = [[32, 15], [15, 40]]  # Covariance matrix of the distribution.

# create sigma points(2n+1个sigma点)
# uses 3 parameters to control how the sigma points are distributed and weighted
points = SigmaPoints(n=2, alpha=.1, beta=2., kappa=1.)  
Wm, Wc = points.weights()
sigmas = points.sigma_points(mean, cov)

# pass through nonlinear function
sigmas_f = np.empty((5, 2))
for i in range(5):  
    sigmas_f[i] = f_nonlinear_xy(sigmas[i, 0], sigmas[i ,1]) 

# use unscented transform to get new mean and covariance
ukf_mean, ukf_cov = unscented_transform(sigmas_f, Wm, Wc)

# generate random points
xs, ys = multivariate_normal(mean, cov, size=1000).T  # 从二维随机变量的正态分布中产生1000个数据点
plot2(xs, ys, f_nonlinear_xy, ukf_mean)

# 画sigma点
plt.xlim(-30, 30); plt.ylim(0, 90)
plt.subplot(121)
plt.scatter(sigmas[:,0], sigmas[:,1], c='r', s=30) 
plt.show()

6.1 实验结果分析

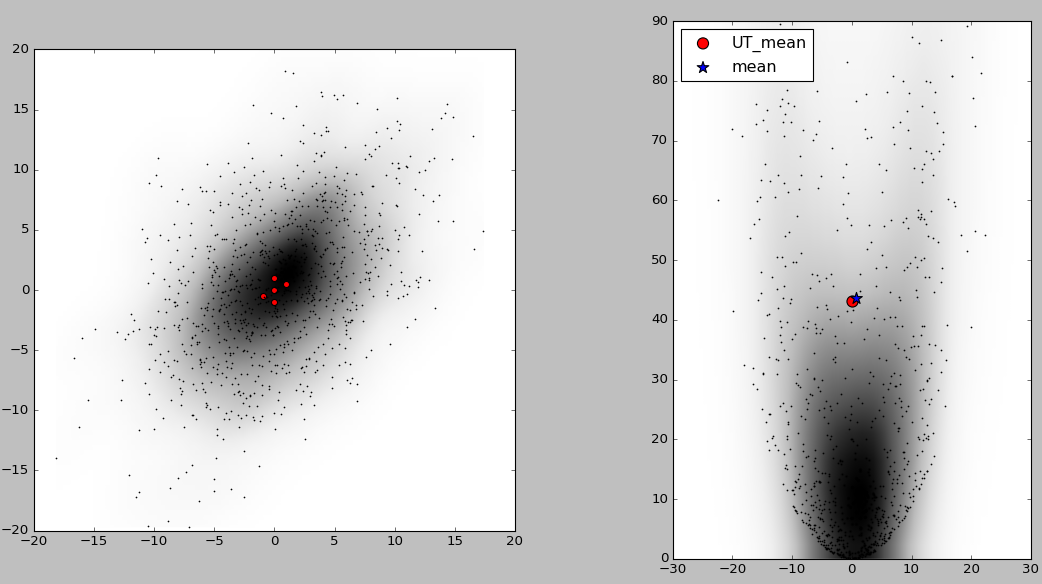
实验结果如下图所示：

左图中黑色散点为随机采样的 1000 1000 1000 个样本点， 5 5 5 个红色标记点为无迹变换的 σ \sigma σ 点；图中阴影的深浅表征概率密度的大小，颜色越深则对应区域的概率密度越大。

右图中红色圆点为基于 5 5 5 个 σ \sigma σ 点经无迹变换得到的近似期望，蓝色星号为 1000 1000 1000 个样本点经非线性变换后直接统计的期望。

实验结论表明：相较于随机采样的直接统计法，无迹变换的计算量得到极大降低，同时二者的计算结果误差处于极小的可接受范围内，体现了无迹变换在非线性系统统计特征求解中高精度、低算力的双重优势。

UKF 原理与实现

td092 原创于 2020-04-21 10:34:40 发布

本文对卡尔曼滤波体系中的无迹卡尔曼滤波（Unscented Kalman Filter, UKF）展开深度解析。UKF 适用于强非线性系统场景，其思路为通过无迹变换（Unscented Transformation, UT）完成状态均值与协方差的推演计算，实现对系统状态的高精度估计。

本文将详细阐述 UT 变换的完整流程，包含采样点的选取规则、非线性映射变换、权值矩阵的确定方法，以及均值矩阵与协方差矩阵的推导计算过程。

卡尔曼滤波体系中主流的滤波方法包含 KF、EKF、UKF 三类。KF 适用于系统方程与量测方程均为线性的场景，EKF 适用于弱非线性场景，UKF 则在强非线性的系统环境中具备更优的估计性能。本文仅针对 UKF 展开阐述。

在 KF 算法中，需求解状态协方差矩阵以推导卡尔曼增益，而受系统非线性特性的影响，该参数仅能获取近似解。EKF 采用雅可比矩阵对非线性系统做一阶泰勒展开实现线性化处理，UKF 则通过随机采样得到的条件均值替代理论均值，基于被估计量与量测量的采样点集合，完成二者自协方差矩阵与互协方差矩阵的求解，该过程即为 U T \boldsymbol {UT} UT 变换。

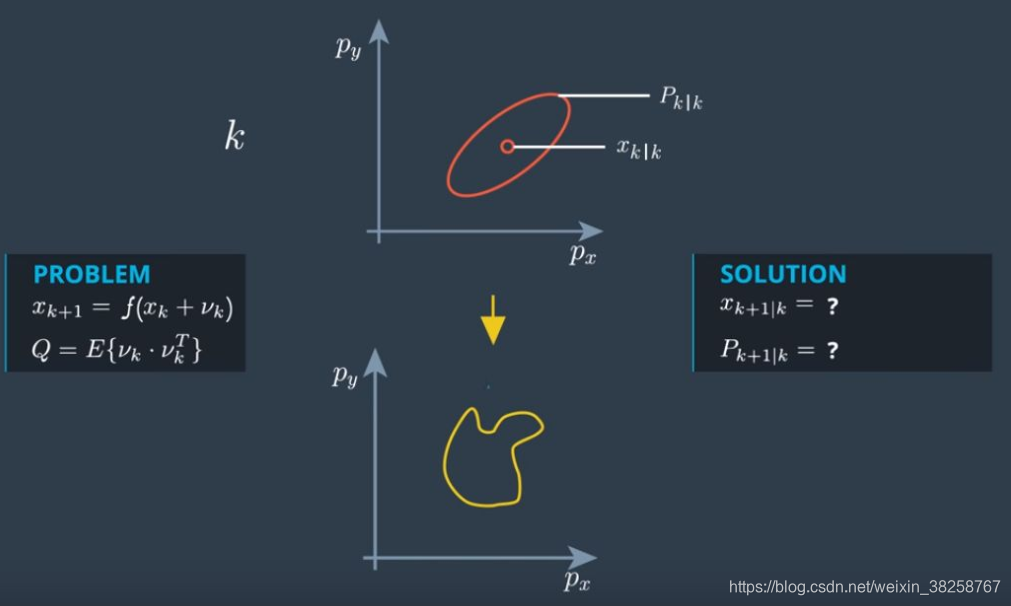
1 UT 变换

针对一维状态变量的场景， U T \boldsymbol {UT} UT 变换的本质可描述为：选取 μ x , μ x + σ x , μ x − σ x \mu_x, \mu_x+\sigma_x, \mu_x-\sigma_x μx,μx+σx,μx−σx 共 3 3 3 个采样点，经非线性映射 g ( ⋅ ) g(\cdot) g(⋅) 完成投影后，对投影后的采样点集拟合高斯分布。

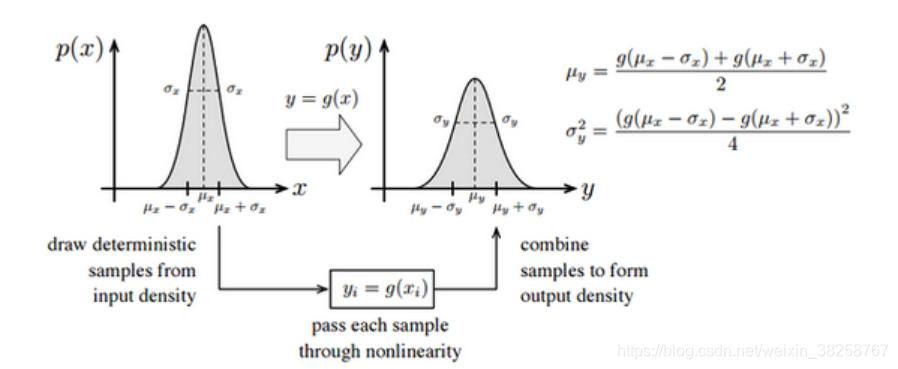
U T \boldsymbol {UT} UT 变换的完整步骤如下：

设 n n n 维随机向量 X X X 经非线性映射 f ( ⋅ ) f(\cdot) f(⋅) 变换后得到 m m m 维随机向量 Y Y Y，满足表达式
Y = f ( X ) Y=f(X) Y=f(X)

在已知随机向量 X X X 的均值 X ˉ \bar{X} Xˉ 与协方差矩阵 P X X P_{XX} PXX 的前提下，求解变换后随机向量 Y Y Y 的均值 Y ˉ \bar{Y} Yˉ 与协方差矩阵 P Y Y P_{YY} PYY。

步骤 1 构造 σ \sigma σ 采样点集

基于随机向量 X X X 的均值 X ˉ \bar{X} Xˉ 与协方差矩阵 P X X P_{XX} PXX，构造共计 2 n + 1 2n+1 2n+1 个 1 倍标准差的 σ \sigma σ 采样点，采样点的生成公式为：
χ ( 0 ) = X ˉ χ ( i ) = X ˉ + ( ( n + λ ) P X X ) ( i ) i = 1 , 2 , ... , n χ ( i ) = X ˉ − ( ( n + λ ) P X X ) ( i − n ) i = n + 1 , n + 2 , ... , 2 n \begin{align} \chi^{(0)} &= \bar{X} \\ \chi^{(i)} &= \bar{X} + \bigl(\sqrt{(n+\lambda) P_{XX}}\bigr){(i)} \quad &i=1,2,\dots,n \\ \chi^{(i)} &= \bar{X} - \bigl(\sqrt{(n+\lambda) P{XX}}\bigr)_{(i-n)} \quad &i=n+1,n+2,\dots,2n \end{align} χ(0)χ(i)χ(i)=Xˉ=Xˉ+((n+λ)PXX )(i)=Xˉ−((n+λ)PXX )(i−n)i=1,2,...,ni=n+1,n+2,...,2n

式中， ( ( n + λ ) P X X ) ( i ) \bigl(\sqrt{(n+\lambda) P_{XX}}\bigr){(i)} ((n+λ)PXX )(i) 代表矩阵 ( n + λ ) P X X (n+\lambda)P{XX} (n+λ)PXX 经下三角分解后得到的平方根矩阵的第 i i i 列，其为 n n n 维列向量。

步骤 2 采样点的非线性映射

对步骤 1 中生成的所有 σ \sigma σ 采样点执行非线性变换，得到映射后的采样点集：
Y ( i ) = f [ χ ( i ) ] i = 0 , 1 , ... , 2 n Y^{(i)}=f\bigl[\chi^{(i)}\bigr] \quad i=0,1,\dots,2n Y(i)=f[χ(i)]i=0,1,...,2n

步骤 3 确定加权系数

定义均值加权系数与协方差加权系数的计算公式如下：
W 0 ( m ) = λ n + λ W 0 ( c ) = λ n + λ + 1 − α 2 + β W i ( m ) = W i ( c ) = 1 2 ( n + λ ) i = 1 , 2 , ... , 2 n \begin{align} W_0^{(m)} &= \frac{\lambda}{n+\lambda} \\ W_0^{(c)} &= \frac{\lambda}{n+\lambda}+1-\alpha^2+\beta \\ W_i^{(m)} &= W_i^{(c)} = \frac{1}{2(n+\lambda)} \quad &i=1,2,\dots,2n \end{align} W0(m)W0(c)Wi(m)=n+λλ=n+λλ+1−α2+β=Wi(c)=2(n+λ)1i=1,2,...,2n

式中，参数 λ \lambda λ 为尺度因子，其计算公式为
λ = α 2 ( n + κ ) − n \lambda = \alpha^2(n+\kappa)-n λ=α2(n+κ)−n

各参数的取值规范为： α \alpha α 为极小正实数，满足 10 − 4 ≤ α ≤ 1 10^{-4}\leq \alpha \leq 1 10−4≤α≤1；常数项取 κ = 3 − n \kappa=3-n κ=3−n； β \beta β 为与随机向量 X X X 概率分布相关的参数，当 X X X 服从正态分布时，取 β = 2 \beta=2 β=2 为最优取值。

步骤 4 求解均值与协方差矩阵

基于加权系数与映射后的采样点集，分别求解随机向量 Y Y Y 的均值与协方差矩阵，近似估计公式为：
Y ˉ ≈ ∑ i = 0 2 n W i ( m ) Y ( i ) P Y Y ≈ ∑ i = 0 2 n W i ( c ) [ Y ( i ) − Y ˉ ] [ Y ( i ) − Y ˉ ] T \begin{align} \bar{Y} &\approx \sum_{i=0}^{2n} W_i^{(m)} Y^{(i)} \\ P_{YY} &\approx \sum_{i=0}^{2n} W_i^{(c)} \bigl[Y^{(i)}-\bar{Y}\bigr]\bigl[Y^{(i)}-\bar{Y}\bigr]^\mathrm{T} \end{align} YˉPYY≈i=0∑2nWi(m)Y(i)≈i=0∑2nWi(c)[Y(i)−Yˉ][Y(i)−Yˉ]T

2 UKF 滤波流程

步骤 1 滤波初值的选取

设定滤波初始时刻的状态估计值与协方差矩阵，表达式如下：
X ^ 0 = E [ X 0 ] P 0 = E [ ( X 0 − X ^ 0 ) ( X 0 − X ^ 0 ) T ] \begin{align} \hat{X}_0 &= \mathbb{E}[X_0] \\ P_0 &= \mathbb{E}\bigl[(X_0-\hat{X}_0)(X_0-\hat{X}_0)^\mathrm{T}\bigr] \end{align} X^0P0=E[X0]=E[(X0−X^0)(X0−X^0)T]

步骤 2 生成 k − 1 k-1 k−1 时刻的 σ \sigma σ 采样点集

基于 k − 1 k-1 k−1 时刻的状态量，构造共计 2 n + 1 2n+1 2n+1 个 σ \sigma σ 采样点，采样点的生成公式为：
χ ( 0 ) = X ˉ χ ( i ) = X ˉ + γ ( P k − 1 ) ( i ) i = 1 , 2 , ... , n χ ( i ) = X ˉ − γ ( P k − 1 ) ( i − n ) i = n + 1 , n + 2 , ... , 2 n \begin{align} \chi^{(0)} &= \bar{X} \\ \chi^{(i)} &= \bar{X} + \gamma \bigl(\sqrt{P_{k-1}}\bigr){(i)} \quad &i=1,2,\dots,n \\ \chi^{(i)} &= \bar{X} - \gamma \bigl(\sqrt{P{k-1}}\bigr)_{(i-n)} \quad &i=n+1,n+2,\dots,2n \end{align} χ(0)χ(i)χ(i)=Xˉ=Xˉ+γ(Pk−1 )(i)=Xˉ−γ(Pk−1 )(i−n)i=1,2,...,ni=n+1,n+2,...,2n

式中，参数 γ \gamma γ 为简化系数，其表达式为
γ = n + λ \gamma = \sqrt{n+\lambda} γ=n+λ

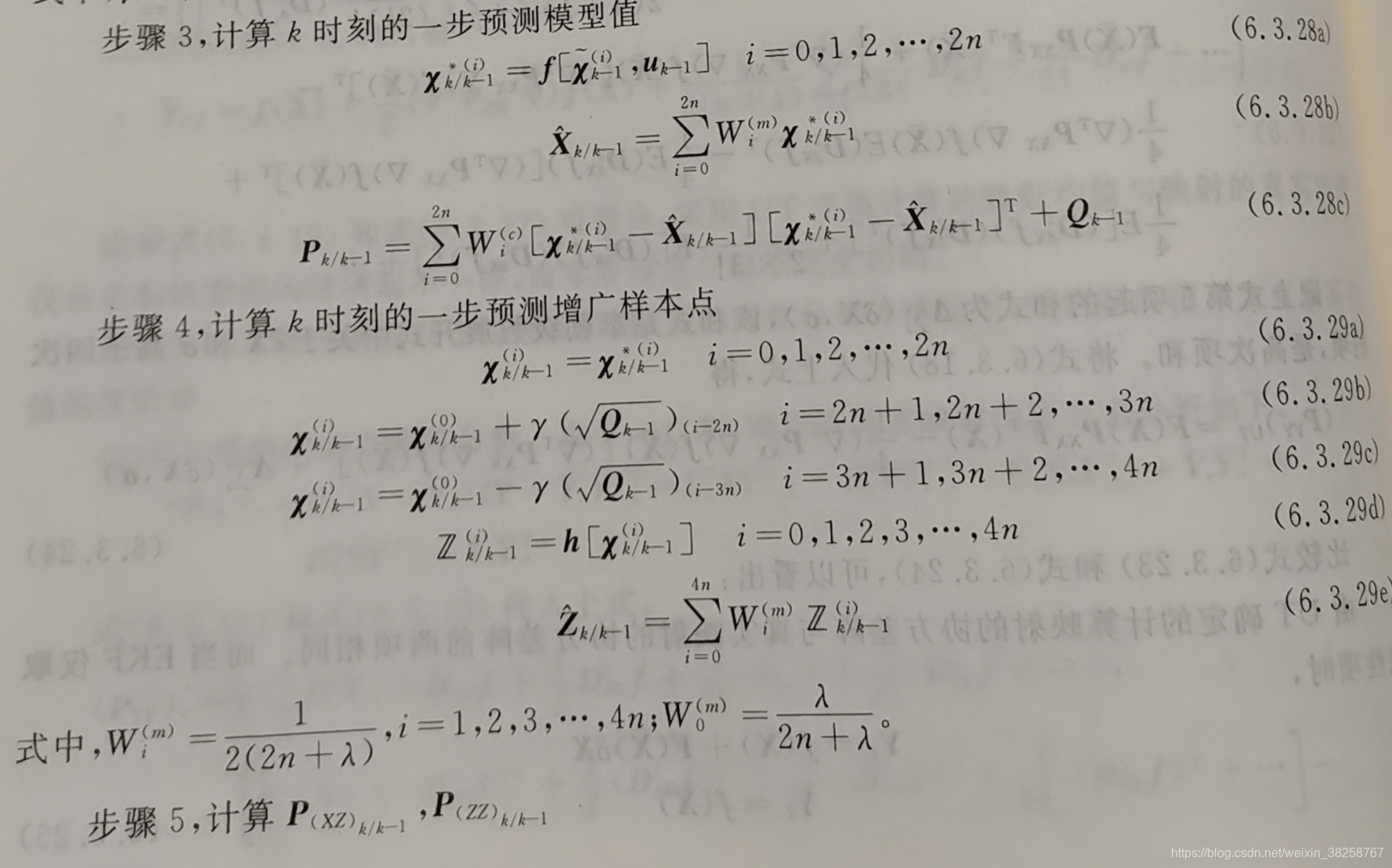
附 实现与参考资料

超详细讲解无迹卡尔曼（UKF）滤波

『蒋小''`花』 原创已于 2023-07-01 11:26:29 修改

1 滤波的应用场景

滤波算法的作用为处理系统的各类不确定性，该类不确定性主要来源于三个方面：

  1. 实际物理系统无法通过完美的数学模型完成精准表征；
  2. 系统运行过程中存在不可控的外部扰动，且扰动的数学建模难度较大；
  3. 各类测量传感器均存在固有测量误差，量测值无法完全等于真实值。

应用示例 1 ：由系统状态方程推导得到的电流值 i 1 i_1 i1，与传感器实测得到的电流值 i 2 i_2 i2，均因上述不确定性存在偏差；通过卡尔曼滤波可对两个来源的信息完成加权融合，求解最接近真实值的最优估计值。

应用示例 2：小红依据经验判断老师当日穿着红色衣物（每周四的规律），小白通过视觉观测判断老师穿着白色衣物（视觉观测存在误差）；卡尔曼滤波可对两种信息的可信度分配权重，最终得到更贴合实际的结论。

2 线性卡尔曼滤波

2.1 系统模型定义

线性系统的状态方程与量测方程满足严格的线性关系，且过程噪声 w k − 1 \boldsymbol{w}{k-1} wk−1与量测噪声 v k \boldsymbol{v}k vk均服从零均值的高斯分布，系统的数学模型为：
x k = A x k − 1 + B U k − 1 + w k − 1 Z k = H x k + v k \begin{aligned} \boldsymbol{x}{k}&= \boldsymbol{A}\boldsymbol{x}{k-1} + \boldsymbol{B}\boldsymbol{U}{k-1} + \boldsymbol{w}{k-1} \\ \boldsymbol{Z}{k}&= \boldsymbol{H}\boldsymbol{x}{k} + \boldsymbol{v}_{k} \end{aligned} xkZk=Axk−1+BUk−1+wk−1=Hxk+vk

其中，过程噪声满足 p ( w ) ∼ N ( 0 , Q ) p(\boldsymbol{w}) \sim \mathcal{N}(0, \boldsymbol{Q}) p(w)∼N(0,Q)，量测噪声满足 p ( v ) ∼ N ( 0 , R ) p(\boldsymbol{v}) \sim \mathcal{N}(0, \boldsymbol{R}) p(v)∼N(0,R)； Q \boldsymbol{Q} Q为过程噪声协方差矩阵， R \boldsymbol{R} R为量测噪声协方差矩阵。

2.2 先验估计

先验估计为基于 k − 1 k-1 k−1时刻的后验状态，对 k k k时刻的状态进行一步预测，得到无实测值修正的预测值，对应的公式为：
x ^ k − = A x ^ k − 1 + B U k − 1 P k − = A P k − 1 A T + Q \widehat{\boldsymbol{x}}{k}^{-}= \boldsymbol{A}\widehat{\boldsymbol{x}}{k-1} + \boldsymbol{B}\boldsymbol{U}{k-1} \\ \boldsymbol{P}{k}^{-}= \boldsymbol{A}\boldsymbol{P}_{k-1}\boldsymbol{A}^{T} + \boldsymbol{Q} x k−=Ax k−1+BUk−1Pk−=APk−1AT+Q

其中， x ^ k − \widehat{\boldsymbol{x}}{k}^{-} x k−为 k k k时刻的状态先验估计值，表征仅通过系统模型得到的预测结果； P k − \boldsymbol{P}{k}^{-} Pk−为状态先验误差协方差矩阵，其物理意义为 e k − = x k − x ^ k − \boldsymbol{e}{k}^{-} = \boldsymbol{x}{k}-\widehat{\boldsymbol{x}}{k}^{-} ek−=xk−x k−的协方差，即 P k − = E [ e k − e k − T ] \boldsymbol{P}{k}^{-} = \mathbb{E}\left[\boldsymbol{e}{k}^{-}\boldsymbol{e}{k}^{-T}\right] Pk−=E[ek−ek−T]，该矩阵用于卡尔曼增益的求解，其迹越小代表先验估计的误差越小。

2.3 后验估计

后验估计为滤波的重要输出，是结合先验预测值与实测值的最优估计，对应的公式为：
x ^ k = x ^ k − + K k ( Z k − H x ^ k − ) K k = P k − H T H P k − H T + R P k = ( I − K k H ) P k − \begin{aligned} \widehat{\boldsymbol{x}}{k}&= \widehat{\boldsymbol{x}}{k}^{-} + \boldsymbol{K}{k}\left(\boldsymbol{Z}{k}-\boldsymbol{H}\widehat{\boldsymbol{x}}{k}^{-}\right) \\ \boldsymbol{K}{k}&= \frac{\boldsymbol{P}{k}^{-}\boldsymbol{H}^{T}}{\boldsymbol{H}\boldsymbol{P}{k}^{-}\boldsymbol{H}^{T}+\boldsymbol{R}} \\ \boldsymbol{P}{k}&= \left(\boldsymbol{I}-\boldsymbol{K}{k}\boldsymbol{H}\right)\boldsymbol{P}_{k}^{-} \end{aligned} x kKkPk=x k−+Kk(Zk−Hx k−)=HPk−HT+RPk−HT=(I−KkH)Pk−

其中， K k \boldsymbol{K}{k} Kk为卡尔曼增益，其取值表征对先验预测与实测值的信任程度： K k \boldsymbol{K}{k} Kk越大，代表越信任实测值； K k \boldsymbol{K}{k} Kk越小，代表越信任系统模型的预测值。后验误差协方差 P k = E [ ( x k − x ^ k ) ( x k − x ^ k ) T ] \boldsymbol{P}{k} = \mathbb{E}\left[(\boldsymbol{x}{k}-\widehat{\boldsymbol{x}}{k})(\boldsymbol{x}{k}-\widehat{\boldsymbol{x}}{k})^{T}\right] Pk=E[(xk−x k)(xk−x k)T]，滤波的目标为使 P k \boldsymbol{P}_{k} Pk的迹最小，即实现估计值与真实值的误差最小。

3 扩展卡尔曼滤波

线性卡尔曼滤波仅适用于线性高斯系统的状态估计，无法直接处理非线性问题------原因是：服从高斯分布的随机变量经过非线性变换后，其分布将不再满足高斯特性。扩展卡尔曼滤波（EKF）的思路为：通过泰勒级数的一阶展开对非线性模型完成局部线性化，将非线性问题转化为线性问题后，再沿用卡尔曼滤波的递推框架完成求解。

3.1 非线性系统模型定义

非线性系统的状态方程与量测方程的一般形式为：
x k = f ( x k − 1 , u k − 1 , w k − 1 ) Z k = h ( x k , v k ) \begin{aligned} \boldsymbol{x}{k}&= \boldsymbol{f}(\boldsymbol{x}{k-1},\boldsymbol{u}{k-1},\boldsymbol{w}{k-1}) \\ \boldsymbol{Z}{k}&= \boldsymbol{h}(\boldsymbol{x}{k},\boldsymbol{v}_{k}) \end{aligned} xkZk=f(xk−1,uk−1,wk−1)=h(xk,vk)

其中， f ( ⋅ ) \boldsymbol{f}(\cdot) f(⋅)为非线性状态转移函数， h ( ⋅ ) \boldsymbol{h}(\cdot) h(⋅)为非线性量测函数；过程噪声 w k − 1 ∼ N ( 0 , Q ) \boldsymbol{w}{k-1} \sim \mathcal{N}(0, \boldsymbol{Q}) wk−1∼N(0,Q)，量测噪声 v k ∼ N ( 0 , R ) \boldsymbol{v}{k} \sim \mathcal{N}(0, \boldsymbol{R}) vk∼N(0,R)。

3.2 泰勒一阶线性化

对非线性函数的线性化过程在当前最优估计点 处完成，原因是真实状态未知，无法在真实值处展开。对状态转移函数 f ( ⋅ ) \boldsymbol{f}(\cdot) f(⋅)在 x ^ k − 1 \widehat{\boldsymbol{x}}{k-1} x k−1处一阶泰勒展开：
f ( x k − 1 ) ≈ f ( x ^ k − 1 ) + F k − 1 ( x k − 1 − x ^ k − 1 ) \boldsymbol{f}(\boldsymbol{x}{k-1}) \approx \boldsymbol{f}(\widehat{\boldsymbol{x}}{k-1}) + \boldsymbol{F}{k-1}\left(\boldsymbol{x}{k-1}-\widehat{\boldsymbol{x}}{k-1}\right) f(xk−1)≈f(x k−1)+Fk−1(xk−1−x k−1)

对量测函数 h ( ⋅ ) \boldsymbol{h}(\cdot) h(⋅)在 x ^ k − \widehat{\boldsymbol{x}}{k}^{-} x k−处一阶泰勒展开：
h ( x k ) ≈ h ( x ^ k − ) + H k ( x k − x ^ k − ) \boldsymbol{h}(\boldsymbol{x}{k}) \approx \boldsymbol{h}(\widehat{\boldsymbol{x}}{k}^{-}) + \boldsymbol{H}{k}\left(\boldsymbol{x}{k}-\widehat{\boldsymbol{x}}{k}^{-}\right) h(xk)≈h(x k−)+Hk(xk−x k−)

其中， F k − 1 = ∂ f ∂ x ∣ x = x ^ k − 1 \boldsymbol{F}{k-1} = \frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}} \bigg|{\boldsymbol{x}=\widehat{\boldsymbol{x}}{k-1}} Fk−1=∂x∂f x=x k−1为状态转移雅克比矩阵， H k = ∂ h ∂ x ∣ x = x ^ k − \boldsymbol{H}{k} = \frac{\partial \boldsymbol{h}}{\partial \boldsymbol{x}} \bigg|{\boldsymbol{x}=\widehat{\boldsymbol{x}}{k}^{-}} Hk=∂x∂h x=x k−为量测雅克比矩阵。

3.3 EKF 递推公式

完成线性化后，EKF 的先验估计与后验估计公式可由线性卡尔曼滤波推广得到，先验估计 ：
x ^ k − = f ( x ^ k − 1 , u k − 1 , 0 ) P k − = F k − 1 P k − 1 F k − 1 T + Q \begin{aligned} \widehat{\boldsymbol{x}}{k}^{-}&= \boldsymbol{f}(\widehat{\boldsymbol{x}}{k-1},\boldsymbol{u}{k-1},0) \\ \boldsymbol{P}{k}^{-}&= \boldsymbol{F}{k-1}\boldsymbol{P}{k-1}\boldsymbol{F}{k-1}^{T} + \boldsymbol{Q} \end{aligned} x k−Pk−=f(x k−1,uk−1,0)=Fk−1Pk−1Fk−1T+Q
后验估计 ：
x ^ k = x ^ k − + K k ( Z k − h ( x ^ k − , 0 ) ) K k = P k − H k T H k P k − H k T + R P k = ( I − K k H k ) P k − \begin{aligned} \widehat{\boldsymbol{x}}{k}&= \widehat{\boldsymbol{x}}{k}^{-} + \boldsymbol{K}{k}\left(\boldsymbol{Z}{k}-\boldsymbol{h}(\widehat{\boldsymbol{x}}{k}^{-},0)\right) \\ \boldsymbol{K}{k}&= \frac{\boldsymbol{P}{k}^{-}\boldsymbol{H}{k}^{T}}{\boldsymbol{H}{k}\boldsymbol{P}{k}^{-}\boldsymbol{H}{k}^{T}+\boldsymbol{R}} \\ \boldsymbol{P}{k}&= \left(\boldsymbol{I}-\boldsymbol{K}{k}\boldsymbol{H}{k}\right)\boldsymbol{P}{k}^{-} \end{aligned} x kKkPk=x k−+Kk(Zk−h(x k−,0))=HkPk−HkT+RPk−HkT=(I−KkHk)Pk−

EKF 与线性卡尔曼滤波的差异为：将线性矩阵 A 、 H \boldsymbol{A}、\boldsymbol{H} A、H替换为雅克比矩阵 F 、 H \boldsymbol{F}、\boldsymbol{H} F、H，将线性映射替换为非线性函数的直接求解。其固有缺陷为：泰勒一阶展开舍弃了高阶项，在强非线性系统中会引入不可忽略的线性化误差；同时雅克比矩阵的求解过程复杂，部分非线性函数甚至无法求得解析的雅克比矩阵。

4 无迹卡尔曼滤波

针对 EKF 的上述缺陷，无迹卡尔曼滤波（UKF）提出了全新的非线性处理思路：不对非线性函数做近似，而是对非线性函数作用的概率密度分布做近似。UKF 无需对非线性模型进行泰勒展开，也无需计算雅克比矩阵，而是通过无迹变换（UT）完成均值与协方差的非线性传递，其对统计矩的近似精度可达二阶，在非线性系统中具备更高的估计精度与数值稳定性。

4.1 无迹变换的原理

无迹变换是处理非线性随机变量传递的方法，其逻辑为：对一个服从某一概率分布的随机向量，按既定规则选取少量采样点（Sigma 点），该组采样点的均值与协方差和原随机向量完全一致；将所有采样点代入非线性函数完成映射后，对映射后的采样点重新加权求和，即可得到非线性变换后随机向量的均值与协方差。

无迹变换的完整流程分为 3 个步骤：

  1. 从原状态分布中按对称采样规则选取 2 n + 1 2n+1 2n+1个 Sigma 采样点，采样点的均值与协方差严格匹配原分布；
  2. 将所有 Sigma 点代入非线性函数，得到非线性映射后的采样点集；
  3. 对映射后的采样点集加权求和，求解变换后随机向量的均值与协方差。

4.2 无迹变换的数学实现

设存在非线性映射 y = f ( x ) \boldsymbol{y} = \boldsymbol{f}(\boldsymbol{x}) y=f(x)， x \boldsymbol{x} x为 n n n维随机向量，已知其均值 x ‾ \overline{\boldsymbol{x}} x、协方差 P \boldsymbol{P} P，无迹变换的具体实现步骤如下。

（1）Sigma 点集的构造

{ X ( 0 ) = x ‾ , i = 0 X ( i ) = x ‾ + ( ( n + λ ) P ) i , i = 1 ∼ n X ( i ) = x ‾ − ( ( n + λ ) P ) i − n , i = n + 1 ∼ 2 n \begin{cases} \boldsymbol{X}^{(0)} = \overline{\boldsymbol{x}}, & i=0 \\ \boldsymbol{X}^{(i)} = \overline{\boldsymbol{x}} + \left(\sqrt{(n+\lambda)\boldsymbol{P}}\right){i}, & i=1\sim n \\ \boldsymbol{X}^{(i)} = \overline{\boldsymbol{x}} - \left(\sqrt{(n+\lambda)\boldsymbol{P}}\right){i-n}, & i=n+1\sim 2n \end{cases} ⎩ ⎨ ⎧X(0)=x,X(i)=x+((n+λ)P )i,X(i)=x−((n+λ)P )i−n,i=0i=1∼ni=n+1∼2n

其中， ( ( n + λ ) P ) i \left(\sqrt{(n+\lambda)\boldsymbol{P}}\right)_{i} ((n+λ)P )i表示矩阵 ( n + λ ) P (n+\lambda)\boldsymbol{P} (n+λ)P乔里斯基分解后的第 i i i列； λ = α 2 ( n + κ ) − n \lambda = \alpha^2(n+\kappa)-n λ=α2(n+κ)−n为缩放参数，工程中常用取值为 α ∈ ( 0 , 1 ] \alpha \in (0,1] α∈(0,1]、 κ ≥ 0 \kappa \ge 0 κ≥0、 β = 2 \beta=2 β=2（适配高斯分布的最优值），简化场景下可取 λ = 3 − n \lambda=3-n λ=3−n。需保证矩阵 ( n + λ ) P (n+\lambda)\boldsymbol{P} (n+λ)P为半正定矩阵，确保分解有效。

（2）Sigma 点的权值分配

为每个 Sigma 点分配均值权值 w m ( i ) w_m^{(i)} wm(i)与协方差权值 w c ( i ) w_c^{(i)} wc(i)，权值满足归一化条件 ∑ i = 0 2 n w m ( i ) = 1 \sum_{i=0}^{2n}w_m^{(i)}=1 ∑i=02nwm(i)=1，具体取值为：
{ w m ( 0 ) = λ n + λ w c ( 0 ) = λ n + λ + ( 1 − α 2 + β ) w m ( i ) = w c ( i ) = 1 2 ( n + λ ) , i = 1 ∼ 2 n \begin{cases} w_m^{(0)} = \frac{\lambda}{n+\lambda} \\ w_c^{(0)} = \frac{\lambda}{n+\lambda} + (1-\alpha^2+\beta) \\ w_m^{(i)} = w_c^{(i)} = \frac{1}{2(n+\lambda)}, & i=1\sim 2n \end{cases} ⎩ ⎨ ⎧wm(0)=n+λλwc(0)=n+λλ+(1−α2+β)wm(i)=wc(i)=2(n+λ)1,i=1∼2n

（3）非线性映射与统计特征求解

将所有 Sigma 点代入非线性函数，得到映射后的采样点集 Y ( i ) = f ( X ( i ) ) \boldsymbol{Y}^{(i)} = \boldsymbol{f}(\boldsymbol{X}^{(i)}) Y(i)=f(X(i))；对映射后的点集加权求和，即可得到输出量 y \boldsymbol{y} y的均值与协方差：
y ‾ = ∑ i = 0 2 n w m ( i ) Y ( i ) P y = ∑ i = 0 2 n w c ( i ) ( Y ( i ) − y ‾ ) ( Y ( i ) − y ‾ ) T \begin{aligned} \overline{\boldsymbol{y}} &= \sum_{i=0}^{2n} w_m^{(i)} \boldsymbol{Y}^{(i)} \\ \boldsymbol{P}y &= \sum{i=0}^{2n} w_c^{(i)} \left(\boldsymbol{Y}^{(i)}-\overline{\boldsymbol{y}}\right)\left(\boldsymbol{Y}^{(i)}-\overline{\boldsymbol{y}}\right)^T \end{aligned} yPy=i=0∑2nwm(i)Y(i)=i=0∑2nwc(i)(Y(i)−y)(Y(i)−y)T

4.3 UKF 完整算法流程

针对非线性系统 { X ( k + 1 ) = f ( x ( k ) , W ( k ) ) Z ( k ) = h ( x ( k ) , V ( k ) ) \begin{cases} \boldsymbol{X}(k+1) = \boldsymbol{f}(\boldsymbol{x}(k),\boldsymbol{W}(k)) \\ \boldsymbol{Z}(k) = \boldsymbol{h}(\boldsymbol{x}(k),\boldsymbol{V}(k)) \end{cases} {X(k+1)=f(x(k),W(k))Z(k)=h(x(k),V(k))，

其中 W ( k ) ∼ N ( 0 , Q ) \boldsymbol{W}(k)\sim\mathcal{N}(0,\boldsymbol{Q}) W(k)∼N(0,Q)， V ( k ) ∼ N ( 0 , R ) \boldsymbol{V}(k)\sim\mathcal{N}(0,\boldsymbol{R}) V(k)∼N(0,R)，

UKF 的完整递推步骤如下：

步骤 1：初始化系统状态

X ^ ( 0 ∣ 0 ) = E [ X ( 0 ) ] , P ( 0 ∣ 0 ) = E [ ( X ( 0 ) − X ^ ( 0 ∣ 0 ) ) ( X ( 0 ) − X ^ ( 0 ∣ 0 ) ) T ] \widehat{\boldsymbol{X}}(0|0) = \mathbb{E}\left[\boldsymbol{X}(0)\right], \quad \boldsymbol{P}(0|0) = \mathbb{E}\left[\left(\boldsymbol{X}(0)-\widehat{\boldsymbol{X}}(0|0)\right)\left(\boldsymbol{X}(0)-\widehat{\boldsymbol{X}}(0|0)\right)^T\right] X (0∣0)=E[X(0)],P(0∣0)=E[(X(0)−X (0∣0))(X(0)−X (0∣0))T]

步骤 2：生成 Sigma 点集

基于 k k k时刻的后验状态，生成 2 n + 1 2n+1 2n+1个 Sigma 点：
X ( i ) ( k ∣ k ) = [ X ^ ( k ∣ k ) , X ^ ( k ∣ k ) + ( n + λ ) P ( k ∣ k ) , X ^ ( k ∣ k ) − ( n + λ ) P ( k ∣ k ) ] \boldsymbol{X}^{(i)}(k|k) = \left[ \widehat{\boldsymbol{X}}(k|k), \widehat{\boldsymbol{X}}(k|k)+\sqrt{(n+\lambda)\boldsymbol{P}(k|k)}, \widehat{\boldsymbol{X}}(k|k)-\sqrt{(n+\lambda)\boldsymbol{P}(k|k)} \right] X(i)(k∣k)=[X (k∣k),X (k∣k)+(n+λ)P(k∣k) ,X (k∣k)−(n+λ)P(k∣k) ]

步骤 3：状态预测（Sigma 点的一步传播）

将所有 Sigma 点代入非线性状态转移函数，完成预测：
X ( i ) ( k + 1 ∣ k ) = f [ k , X ( i ) ( k ∣ k ) ] \boldsymbol{X}^{(i)}(k+1|k) = \boldsymbol{f}\left[k, \boldsymbol{X}^{(i)}(k|k)\right] X(i)(k+1∣k)=f[k,X(i)(k∣k)]

步骤 4：求解状态先验均值与协方差

对预测后的 Sigma 点加权求和，得到先验估计值，同时引入过程噪声协方差：
X ^ ( k + 1 ∣ k ) = ∑ i = 0 2 n w ( i ) X ( i ) ( k + 1 ∣ k ) P ( k + 1 ∣ k ) = ∑ i = 0 2 n w ( i ) [ X ( i ) ( k + 1 ∣ k ) − X ^ ( k + 1 ∣ k ) ] [ X ( i ) ( k + 1 ∣ k ) − X ^ ( k + 1 ∣ k ) ] T + Q \begin{aligned} \widehat{\boldsymbol{X}}(k+1|k) &= \sum_{i=0}^{2n} w^{(i)} \boldsymbol{X}^{(i)}(k+1|k) \\ \boldsymbol{P}(k+1|k) &= \sum_{i=0}^{2n} w^{(i)} \left[\boldsymbol{X}^{(i)}(k+1|k)-\widehat{\boldsymbol{X}}(k+1|k)\right]\left[\boldsymbol{X}^{(i)}(k+1|k)-\widehat{\boldsymbol{X}}(k+1|k)\right]^T + \boldsymbol{Q} \end{aligned} X (k+1∣k)P(k+1∣k)=i=0∑2nw(i)X(i)(k+1∣k)=i=0∑2nw(i)[X(i)(k+1∣k)−X (k+1∣k)][X(i)(k+1∣k)−X (k+1∣k)]T+Q

步骤 5：量测空间的 Sigma 点生成与映射

基于状态先验值重新生成 Sigma 点集，并代入非线性量测函数完成量测预测：
X ^ ( i ) ( k + 1 ∣ k ) = [ X ^ ( k + 1 ∣ k ) , X ^ ( k + 1 ∣ k ) + ( n + λ ) P ( k + 1 ∣ k ) , X ^ ( k + 1 ∣ k ) − ( n + λ ) P ( k + 1 ∣ k ) ] Z ( i ) ( k + 1 ∣ k ) = h [ X ^ ( i ) ( k + 1 ∣ k ) ] \begin{aligned} \widehat{\boldsymbol{X}}^{(i)}(k+1|k) &= \left[ \widehat{\boldsymbol{X}}(k+1|k), \widehat{\boldsymbol{X}}(k+1|k)+\sqrt{(n+\lambda)\boldsymbol{P}(k+1|k)}, \widehat{\boldsymbol{X}}(k+1|k)-\sqrt{(n+\lambda)\boldsymbol{P}(k+1|k)} \right] \\ \boldsymbol{Z}^{(i)}(k+1|k) &= \boldsymbol{h}\left[ \widehat{\boldsymbol{X}}^{(i)}(k+1|k) \right] \end{aligned} X (i)(k+1∣k)Z(i)(k+1∣k)=[X (k+1∣k),X (k+1∣k)+(n+λ)P(k+1∣k) ,X (k+1∣k)−(n+λ)P(k+1∣k) ]=h[X (i)(k+1∣k)]

步骤 6：求解量测先验均值、协方差与交叉协方差

Z ‾ ( k + 1 ∣ k ) = ∑ i = 0 2 n w ( i ) Z ( i ) ( k + 1 ∣ k ) P z z = ∑ i = 0 2 n w ( i ) [ Z ( i ) ( k + 1 ∣ k ) − Z ‾ ( k + 1 ∣ k ) ] [ Z ( i ) ( k + 1 ∣ k ) − Z ‾ ( k + 1 ∣ k ) ] T + R P x z = ∑ i = 0 2 n w ( i ) [ X ^ ( i ) ( k + 1 ∣ k ) − X ^ ( k + 1 ∣ k ) ] [ Z ( i ) ( k + 1 ∣ k ) − Z ‾ ( k + 1 ∣ k ) ] T \begin{aligned} \overline{\boldsymbol{Z}}(k+1|k) &= \sum_{i=0}^{2n} w^{(i)} \boldsymbol{Z}^{(i)}(k+1|k) \\ \boldsymbol{P}{zz} &= \sum{i=0}^{2n} w^{(i)} \left[\boldsymbol{Z}^{(i)}(k+1|k)-\overline{\boldsymbol{Z}}(k+1|k)\right]\left[\boldsymbol{Z}^{(i)}(k+1|k)-\overline{\boldsymbol{Z}}(k+1|k)\right]^T + \boldsymbol{R} \\ \boldsymbol{P}{xz} &= \sum{i=0}^{2n} w^{(i)} \left[\widehat{\boldsymbol{X}}^{(i)}(k+1|k)-\widehat{\boldsymbol{X}}(k+1|k)\right]\left[\boldsymbol{Z}^{(i)}(k+1|k)-\overline{\boldsymbol{Z}}(k+1|k)\right]^T \end{aligned} Z(k+1∣k)PzzPxz=i=0∑2nw(i)Z(i)(k+1∣k)=i=0∑2nw(i)[Z(i)(k+1∣k)−Z(k+1∣k)][Z(i)(k+1∣k)−Z(k+1∣k)]T+R=i=0∑2nw(i)[X (i)(k+1∣k)−X (k+1∣k)][Z(i)(k+1∣k)−Z(k+1∣k)]T

步骤 7：卡尔曼增益求解与状态更新

K ( k + 1 ) = P x z P z z − 1 X ^ ( k + 1 ∣ k + 1 ) = X ^ ( k + 1 ∣ k ) + K ( k + 1 ) [ Z ( k + 1 ) − Z ‾ ( k + 1 ∣ k ) ] P ( k + 1 ∣ k + 1 ) = P ( k + 1 ∣ k ) − K ( k + 1 ) P z z K ( k + 1 ) T \begin{aligned} \boldsymbol{K}(k+1) &= \boldsymbol{P}{xz} \boldsymbol{P}{zz}^{-1} \\ \widehat{\boldsymbol{X}}(k+1|k+1) &= \widehat{\boldsymbol{X}}(k+1|k) + \boldsymbol{K}(k+1)\left[ \boldsymbol{Z}(k+1)-\overline{\boldsymbol{Z}}(k+1|k) \right] \\ \boldsymbol{P}(k+1|k+1) &= \boldsymbol{P}(k+1|k) - \boldsymbol{K}(k+1)\boldsymbol{P}_{zz}\boldsymbol{K}(k+1)^T \end{aligned} K(k+1)X (k+1∣k+1)P(k+1∣k+1)=PxzPzz−1=X (k+1∣k)+K(k+1)[Z(k+1)−Z(k+1∣k)]=P(k+1∣k)−K(k+1)PzzK(k+1)T

实际应用（仿真分析）

4.1 仿真系统模型

本次仿真选取的状态方程与量测方程如下，其中状态向量为二维运动的位置与速度，量测为非线性的距离量测：
X ( k + 1 ) = Φ X ( k ) + Γ W ( k ) Z ( k ) = ( x ( k ) − x 0 ) 2 + ( y ( k ) − y 0 ) 2 + V ( k ) \begin{aligned} \boldsymbol{X}(k+1) &= \boldsymbol{\Phi} \boldsymbol{X}(k) + \boldsymbol{\Gamma} \boldsymbol{W}(k) \\[1em] \boldsymbol{Z}(k) &= \sqrt{(x(k)-x_0)^2+(y(k)-y_0)^2} + \boldsymbol{V}(k) \end{aligned} X(k+1)Z(k)=ΦX(k)+ΓW(k)=(x(k)−x0)2+(y(k)−y0)2 +V(k)

式中各矩阵取值为：
Φ = [ 1 1 0 0 0 1 0 0 0 0 1 1 0 0 0 1 ] , Γ = [ 0.5 0 1 0 0 0.5 0 1 ] , Q = σ w ⋅ d i a g ( [ 1 , 1 ] ) , R = 5 \boldsymbol{\Phi}= \begin{bmatrix}1&1&0&0\\0&1&0&0\\0&0&1&1\\0&0&0&1\end{bmatrix}, \boldsymbol{\Gamma}= \begin{bmatrix}0.5&0\\1&0\\0&0.5\\0&1\end{bmatrix}, \boldsymbol{Q}=\sigma_w \cdot diag([1,1]), \boldsymbol{R}=5 Φ= 1000110000100011 ,Γ= 0.5100000.51 ,Q=σw⋅diag([1,1]),R=5

系统的真实状态为
X r e a l ( k ) = [ x r e a l ( k ) , x ˙ r e a l ( k ) , y r e a l ( k ) , y ˙ r e a l ( k ) ] T ， \boldsymbol{X}{real}(k) = [x{real}(k),\dot{x}{real}(k),y{real}(k),\dot{y}_{real}(k)]^T， Xreal(k)=[xreal(k),x˙real(k),yreal(k),y˙real(k)]T，

UKF 滤波估计状态为
X U K F ( k ) = [ x U K F ( k ) , x ˙ U K F ( k ) , y U K F ( k ) , y ˙ U K F ( k ) ] T \boldsymbol{X}{UKF}(k) = [x{UKF}(k),\dot{x}{UKF}(k),y{UKF}(k),\dot{y}_{UKF}(k)]^T XUKF(k)=[xUKF(k),x˙UKF(k),yUKF(k),y˙UKF(k)]T

4.2 误差评价指标

定义均方根误差（RMSE）作为滤波精度的评价指标，表征估计值与真实值的偏差程度：
RMSE ( k ) = ( x U K F ( k ) − x r e a l ( k ) ) 2 + ( y U K F ( k ) − y r e a l ( k ) ) 2 \text{RMSE}(k) = \sqrt{(x_{UKF}(k)-x_{real}(k))^2 + (y_{UKF}(k)-y_{real}(k))^2} RMSE(k)=(xUKF(k)−xreal(k))2+(yUKF(k)−yreal(k))2

RMSE 越小，代表滤波算法的估计精度越高。

4.3 MATLAB 仿真代码

matlab 复制代码 
%% 无迹卡尔曼滤波 仿真实现
clear;clc;close all;
T = 1;          % 时间步长
N = 60/T;       % 仿真总步数
n = 4;          % 状态维度 x=[x,dx,y,dy]

%% 1. 系统参数初始化
X = zeros(n,N);             % 真实状态矩阵
X(:,1) = [-100,2,200,20]';  % 初始状态
Z = zeros(1,N);             % 量测值矩阵
delta_w = 1e-3;
Q = delta_w * diag([0.5,1]);% 过程噪声协方差
G = [T^2/2,0;T,0;0,T^2/2;0,T]; % 噪声驱动矩阵
R = 5;                      % 量测噪声方差
F = [1,T,0,0;0,1,0,0;0,0,1,T;0,0,0,1]; % 状态转移矩阵
x0 = 200;y0 = 300;          % 量测参考点
Xstation = [x0,y0];
v = sqrt(R)*randn(1,N);     % 量测噪声

%% 2. 生成真实状态与量测值
for t = 2:N
    X(:,t) = F*X(:,t-1) + G*sqrtm(Q)*randn(2,1);
end
for t = 1:N
    Z(t) = Dist(X(:,t),Xstation) + v(t);
end

%% 3. UKF 参数配置
L = n;
alpha = 1;
kappa = 0;
beta = 2;
lambda = 3 - L;             % 缩放参数 λ=3-n
% 权值分配
Wm = ones(1,2*L+1)/(2*(L+lambda));
Wc = ones(1,2*L+1)/(2*(L+lambda));
Wm(1) = lambda/(L+lambda);
Wc(1) = lambda/(L+lambda) + (1-alpha^2+beta);

%% 4. UKF 初始化
Xukf = zeros(n,N);      % UKF估计状态
Xukf(:,1) = X(:,1);     % 初始估计值
P0 = eye(n);            % 初始协方差矩阵

%% 5. UKF 递推滤波主循环
for t = 2:N
    xestimate = Xukf(:,t-1);
    P = P0;
    
    % 步骤1：生成Sigma点集
    cho = chol(P*(L+lambda))';
    xgamaP1 = zeros(n,L);xgamaP2 = zeros(n,L);
    for k = 1:L
        xgamaP1(:,k) = xestimate + cho(:,k);
        xgamaP2(:,k) = xestimate - cho(:,k);
    end
    Xsigma = [xestimate, xgamaP1, xgamaP2];
    
    % 步骤2：Sigma点状态预测
    Xsigmapre = F * Xsigma;
    
    % 步骤3：计算状态先验均值与协方差
    Xpred = zeros(n,1);
    for k = 1:2*L+1
        Xpred = Xpred + Wm(k)*Xsigmapre(:,k);
    end
    Ppred = zeros(n,n);
    for k = 1:2*L+1
        Ppred = Ppred + Wc(k)*(Xsigmapre(:,k)-Xpred)*(Xsigmapre(:,k)-Xpred)';
    end
    Ppred = Ppred + G*Q*G';
    
    % 步骤4：量测空间Sigma点生成与映射
    chor = chol((L+lambda)*Ppred)';
    XaugsigmaP1 = zeros(n,L);XaugsigmaP2 = zeros(n,L);
    for k = 1:L
        XaugsigmaP1(:,k) = Xpred + chor(:,k);
        XaugsigmaP2(:,k) = Xpred - chor(:,k);
    end
    Xaugsigma = [Xpred, XaugsigmaP1, XaugsigmaP2];
    Zsigmapre = zeros(1,2*L+1);
    for k = 1:2*L+1
        Zsigmapre(1,k) = hfun(Xaugsigma(:,k),Xstation);
    end
    
    % 步骤5：计算量测先验均值与协方差
    Zpred = 0;
    for k = 1:2*L+1
        Zpred = Zpred + Wm(k)*Zsigmapre(1,k);
    end
    Pzz = 0;
    for k = 1:2*L+1
        Pzz = Pzz + Wc(k)*(Zsigmapre(1,k)-Zpred)*(Zsigmapre(1,k)-Zpred)';
    end
    Pzz = Pzz + R;
    
    % 步骤6：计算交叉协方差与卡尔曼增益
    Pxz = zeros(n,1);
    for k = 1:2*L+1
        Pxz = Pxz + Wc(k)*(Xaugsigma(:,k)-Xpred)*(Zsigmapre(1,k)-Zpred)';
    end
    K = Pxz * inv(Pzz);
    
    % 步骤7：状态与协方差更新
    xestimate = Xpred + K*(Z(t)-Zpred);
    P = Ppred - K*Pzz*K';
    P0 = P;
    Xukf(:,t) = xestimate;
end

%% 6. 计算滤波误差并绘图
for i = 1:N
    Err_KalmanFilter(i) = Dist(X(:,i),Xukf(:,i));
end
% 轨迹对比图
figure;hold on;box on;grid on;
plot(X(1,:),X(3,:),'-k.','LineWidth',1.2);
plot(Xukf(1,:),Xukf(3,:),'-r+','LineWidth',1.2);
legend('真实轨迹','UKF 估计轨迹','Location','best');
xlabel('X 位置');ylabel('Y 位置');title('UKF 滤波轨迹对比');
% 误差曲线图
figure;hold on;box on;grid on;
plot(Err_KalmanFilter,'-ks','MarkerFace','r','LineWidth',1);
xlabel('迭代步数');ylabel('均方根误差 RMSE');title('UKF 滤波误差曲线');
end

%% 子函数1：计算两点间距离
function d = Dist(X1,X2)
    if length(X2)<=2
        d = sqrt((X1(1)-X2(1))^2 + (X1(3)-X2(2))^2);
    else
        d = sqrt((X1(1)-X2(1))^2 + (X1(3)-X2(3))^2);
    end
end

%% 子函数2：非线性量测函数
function y = hfun(x,xx)
    y = sqrt((x(1)-xx(1))^2 + (x(3)-xx(2))^2);
end

无迹卡尔曼滤波算法------基本原理（附 MATLAB 程序）

leon625 原创已于 2024-08-21 11:40:49 修改

无迹卡尔曼滤波（Unscented Kalman Filter, UKF）是一类适用于非线性系统的递推式状态估计算法，相较于扩展卡尔曼滤波（EKF），UKF 在处理非线性问题时具备更高的估计精度与数值稳健性。其优势为通过无迹变换（Unscented Transform, UT）直接对非线性分布进行近似，无需对非线性函数做泰勒展开，也无需计算复杂的雅克比矩阵，对强非线性系统的适配性更强。

一、无迹卡尔曼滤波算法的基本原理

UKF 的思想为：通过构造一组确定的 Sigma 采样点表征系统状态的概率分布，该组采样点的均值与协方差和原状态分布严格一致；将采样点代入非线性函数完成映射后，通过加权求和恢复映射后的概率分布特征（均值与协方差），最终沿用卡尔曼滤波的框架完成状态更新。整个过程未对非线性模型做任何近似，仅对概率分布做合理近似，是一种更贴合非线性系统本质的滤波方法。

主要步骤

1. 生成 Sigma 点

针对 n n n维状态向量 x \boldsymbol{x} x与协方差矩阵 P \boldsymbol{P} P，生成 2 n + 1 2n+1 2n+1个 Sigma 采样点，采样规则满足对称分布，公式为：
{ X ( 0 ) = x ^ X ( i ) = x ^ + ( n + λ ) P i , i = 1 , ... , n X ( i ) = x ^ − ( n + λ ) P i − n , i = n + 1 , ... , 2 n \begin{cases} \boldsymbol{X}^{(0)} = \widehat{\boldsymbol{x}} \\ \boldsymbol{X}^{(i)} = \widehat{\boldsymbol{x}} + \sqrt{(n+\lambda)\boldsymbol{P}}i, & i=1,\dots,n \\ \boldsymbol{X}^{(i)} = \widehat{\boldsymbol{x}} - \sqrt{(n+\lambda)\boldsymbol{P}}{i-n}, & i=n+1,\dots,2n \end{cases} ⎩ ⎨ ⎧X(0)=x X(i)=x +(n+λ)P i,X(i)=x −(n+λ)P i−n,i=1,...,ni=n+1,...,2n

其中， λ \lambda λ为缩放参数，取值为 λ = α 2 ( n + κ ) − n \lambda = \alpha^2(n+\kappa)-n λ=α2(n+κ)−n，用于调节采样点的分布范围； n n n为状态向量的维度。

2. 预测 Sigma 点

将生成的 Sigma 点代入非线性状态转移函数 f ( ⋅ ) \boldsymbol{f}(\cdot) f(⋅)，完成所有采样点的一步预测，得到预测域的 Sigma 点集：
X k + 1 ∣ k ( i ) = f ( X k ∣ k ( i ) ) \boldsymbol{X}{k+1|k}^{(i)} = \boldsymbol{f}\left(\boldsymbol{X}{k|k}^{(i)}\right) Xk+1∣k(i)=f(Xk∣k(i))

3. 计算预测均值和协方差

对预测后的 Sigma 点集加权求和，得到状态的先验均值与协方差，同时叠加过程噪声的影响：
x ^ k + 1 ∣ k = ∑ i = 0 2 n w i X k + 1 ∣ k ( i ) \widehat{\boldsymbol{x}}{k+1|k} = \sum{i=0}^{2n} w_i \boldsymbol{X}{k+1|k}^{(i)} x k+1∣k=i=0∑2nwiXk+1∣k(i)
P k + 1 ∣ k = ∑ i = 0 2 n w i ( X k + 1 ∣ k ( i ) − x ^ k + 1 ∣ k ) ( X k + 1 ∣ k ( i ) − x ^ k + 1 ∣ k ) T + Q \boldsymbol{P}{k+1|k} = \sum_{i=0}^{2n} w_i \left(\boldsymbol{X}{k+1|k}^{(i)}-\widehat{\boldsymbol{x}}{k+1|k}\right)\left(\boldsymbol{X}{k+1|k}^{(i)}-\widehat{\boldsymbol{x}}{k+1|k}\right)^T + \boldsymbol{Q} Pk+1∣k=i=0∑2nwi(Xk+1∣k(i)−x k+1∣k)(Xk+1∣k(i)−x k+1∣k)T+Q

其中， w i w_i wi为 Sigma 点的加权系数， Q \boldsymbol{Q} Q为过程噪声协方差矩阵。

4. 预测测量

将状态预测域的 Sigma 点代入非线性量测函数 h ( ⋅ ) \boldsymbol{h}(\cdot) h(⋅)，映射至量测空间得到量测域的 Sigma 点集：
Z k + 1 ∣ k ( i ) = h ( X k + 1 ∣ k ( i ) ) \boldsymbol{Z}{k+1|k}^{(i)} = \boldsymbol{h}\left(\boldsymbol{X}{k+1|k}^{(i)}\right) Zk+1∣k(i)=h(Xk+1∣k(i))

5. 计算测量均值和协方差

对量测域的 Sigma 点集加权求和，得到量测的先验均值、量测协方差与状态-量测交叉协方差，叠加量测噪声的影响：
z ^ k + 1 ∣ k = ∑ i = 0 2 n w i Z k + 1 ∣ k ( i ) \widehat{\boldsymbol{z}}{k+1|k} = \sum{i=0}^{2n} w_i \boldsymbol{Z}{k+1|k}^{(i)} z k+1∣k=i=0∑2nwiZk+1∣k(i)
P z z = ∑ i = 0 2 n w i ( Z k + 1 ∣ k ( i ) − z ^ k + 1 ∣ k ) ( Z k + 1 ∣ k ( i ) − z ^ k + 1 ∣ k ) T + R \boldsymbol{P}{zz} = \sum_{i=0}^{2n} w_i \left(\boldsymbol{Z}{k+1|k}^{(i)}-\widehat{\boldsymbol{z}}{k+1|k}\right)\left(\boldsymbol{Z}{k+1|k}^{(i)}-\widehat{\boldsymbol{z}}{k+1|k}\right)^T + \boldsymbol{R} Pzz=i=0∑2nwi(Zk+1∣k(i)−z k+1∣k)(Zk+1∣k(i)−z k+1∣k)T+R
P x z = ∑ i = 0 2 n w i ( X k + 1 ∣ k ( i ) − x ^ k + 1 ∣ k ) ( Z k + 1 ∣ k ( i ) − z ^ k + 1 ∣ k ) T \boldsymbol{P}{xz} = \sum{i=0}^{2n} w_i \left(\boldsymbol{X}{k+1|k}^{(i)}-\widehat{\boldsymbol{x}}{k+1|k}\right)\left(\boldsymbol{Z}{k+1|k}^{(i)}-\widehat{\boldsymbol{z}}{k+1|k}\right)^T Pxz=i=0∑2nwi(Xk+1∣k(i)−x k+1∣k)(Zk+1∣k(i)−z k+1∣k)T

其中， R \boldsymbol{R} R为量测噪声协方差矩阵。

6. 更新

求解卡尔曼增益，并完成状态与协方差的后验更新，得到最优估计值：
K k + 1 = P x z P z z − 1 \boldsymbol{K}{k+1} = \boldsymbol{P}{xz} \boldsymbol{P}{zz}^{-1} Kk+1=PxzPzz−1
x ^ k + 1 ∣ k + 1 = x ^ k + 1 ∣ k + K k + 1 ( z k + 1 − z ^ k + 1 ∣ k ) \widehat{\boldsymbol{x}}{k+1|k+1} = \widehat{\boldsymbol{x}}{k+1|k} + \boldsymbol{K}{k+1}\left(\boldsymbol{z}{k+1}-\widehat{\boldsymbol{z}}{k+1|k}\right) x k+1∣k+1=x k+1∣k+Kk+1(zk+1−z k+1∣k)
P k + 1 ∣ k + 1 = P k + 1 ∣ k − K k + 1 P z z K k + 1 T \boldsymbol{P}{k+1|k+1} = \boldsymbol{P}{k+1|k} - \boldsymbol{K}{k+1}\boldsymbol{P}{zz}\boldsymbol{K}_{k+1}^T Pk+1∣k+1=Pk+1∣k−Kk+1PzzKk+1T

其中， z k + 1 \boldsymbol{z}_{k+1} zk+1为 k + 1 k+1 k+1时刻的实际量测值。

二、无迹卡尔曼滤波的优点

  1. 非线性适配性强：UKF 对非线性函数的概率密度分布直接近似，避免了 EKF 泰勒展开的线性化误差，在强非线性系统中具备显著更高的估计精度，其近似精度可达二阶。
  2. 计算复杂度低：无需推导与求解雅克比矩阵，仅需完成采样点的非线性映射与矩阵运算，工程实现难度远低于 EKF，尤其适用于无解析雅克比矩阵的非线性系统。
  3. 数值稳定性好：滤波过程中仅需对正定矩阵做乔里斯基分解，不存在 EKF 中雅克比矩阵奇异导致的滤波发散问题，鲁棒性更强。
  4. 通用性高：可无缝适配线性系统（退化为线性卡尔曼滤波）与非线性系统，无需对模型做额外修改。

三、应用场景

UKF 凭借其优异的非线性处理能力与估计精度，被广泛应用于各类存在非线性特性的工程领域，典型应用场景包括：

  1. 无人驾驶汽车：车辆位姿估计、目标跟踪、传感器融合（激光雷达+毫米波雷达+视觉）等场景，适配车辆运动的非线性模型。
  2. 机器人控制：移动机器人的自主定位与导航、机械臂的运动状态估计，处理机器人动力学的强非线性特性。
  3. 飞行控制：无人机、航天器的姿态与位置估计，适配飞行器的非线性动力学与运动学模型。
  4. 导航与制导：惯性导航与卫星导航的组合滤波，处理惯性器件的非线性误差模型。
  5. 金融数据分析：金融时间序列的预测与风险评估，处理金融市场的非线性波动特性。

无迹卡尔曼滤波是目前非线性滤波领域的经典算法之一，其在精度、复杂度与稳定性之间取得了极佳的平衡，是解决非线性状态估计问题的优选方法。

四、MATLAB 仿真程序

1. 设置系统模型

matlab 复制代码 
% 无迹卡尔曼滤波 通用实现模板
clear;clc;close all;
%% 1. 系统基础参数配置
n = 4;  % 状态维度 x = [x, dx, y, dy]^T
m = 2;  % 观测维度 z = [x^2, y^2]^T

% 初始状态与协方差
x0 = [0; 0; 1; 1];               % 初始状态值
P0 = eye(n);                     % 初始协方差矩阵

% 噪声协方差矩阵
Q = 0.1 * eye(n);                % 过程噪声协方差
R = 0.1 * eye(m);                % 观测噪声协方差

% 非线性函数定义
f = @(x) [x(1)+x(3); x(2)+x(4); x(3); x(4)];  % 状态转移函数
h = @(x) [x(1)^2; x(2)^2];                     % 量测函数

% 仿真时间参数
dt = 0.1;    % 时间步长
T = 10;      % 仿真总时长
time = 0:dt:T;
N = length(time);

2. 无迹卡尔曼滤波器实现

matlab 复制代码 
%% 2. UKF 参数配置
alpha = 1e-3;   % 缩放参数，控制sigma点分布
beta = 2;       % 适配高斯分布的最优值
kappa = 0;      % 辅助参数
lambda = alpha^2*(n+kappa) - n;  % 缩放系数
c = n + lambda;                  % 权重归一化常数

% 计算sigma点权重
Wm = [lambda/c; repmat(1/(2*c), 2*n, 1)];  % 均值权重
Wc = [lambda/c + (1-alpha^2+beta); repmat(1/(2*c), 2*n, 1)];  % 协方差权重

%% 3. 滤波初始化
x_est = x0;    % 状态估计值初始化
P_est = P0;    % 协方差矩阵初始化

% 结果存储矩阵
X_est = zeros(n, N);   % 估计状态
X_true = zeros(n, N);  % 真实状态
Y_meas = zeros(m, N);  % 量测值

X_true(:,1) = x0;
Y_meas(:,1) = h(x0) + sqrtm(R)*randn(m,1);

%% 4. UKF 递推滤波主循环
for t = 2:N
    % 步骤1：生成Sigma点集
    sqrt_P = sqrtm(P_est);
    X_sig = [x_est, x_est+sqrt_P, x_est-sqrt_P];
    
    % 步骤2：Sigma点状态预测
    X_sig_pred = zeros(n, 2*n+1);
    for i = 1:2*n+1
        X_sig_pred(:,i) = f(X_sig(:,i));
    end
    
    % 步骤3：计算状态先验均值与协方差
    x_pred = X_sig_pred * Wm;
    P_pred = Q;
    for i = 1:2*n+1
        P_pred = P_pred + Wc(i)*(X_sig_pred(:,i)-x_pred)*(X_sig_pred(:,i)-x_pred)';
    end
    
    % 步骤4：Sigma点量测预测
    Y_sig_pred = zeros(m, 2*n+1);
    for i = 1:2*n+1
        Y_sig_pred(:,i) = h(X_sig_pred(:,i));
    end
    
    % 步骤5：计算量测先验均值、协方差与交叉协方差
    y_pred = Y_sig_pred * Wm;
    P_yy = R;
    P_xy = zeros(n, m);
    for i = 1:2*n+1
        P_yy = P_yy + Wc(i)*(Y_sig_pred(:,i)-y_pred)*(Y_sig_pred(:,i)-y_pred)';
        P_xy = P_xy + Wc(i)*(X_sig_pred(:,i)-x_pred)*(Y_sig_pred(:,i)-y_pred)';
    end
    
    % 步骤6：计算卡尔曼增益与状态更新
    K = P_xy / P_yy;
    z_meas = h(X_true(:,t-1)) + sqrtm(R)*randn(m,1);  % 生成量测值
    x_est = x_pred + K*(z_meas - y_pred);
    P_est = P_pred - K*P_yy*K';
    
    % 生成真实状态
    X_true(:,t) = f(X_true(:,t-1)) + sqrtm(Q)*randn(n,1);
    
    % 存储结果
    X_est(:,t) = x_est;
    Y_meas(:,t) = z_meas;
end

3. 绘制结果

matlab 复制代码 
%% 5. 结果可视化
figure('Color','w');
% X方向位置对比
subplot(2,1,1);
plot(time, X_true(1,:), 'g-', 'LineWidth',1.2);hold on;
plot(time, X_est(1,:), 'b--', 'LineWidth',1.2);
legend('真实X位置','UKF估计X位置','Location','best');
xlabel('时间 / s');ylabel('X 位置');grid on;

% Y方向位置对比
subplot(2,1,2);
plot(time, X_true(2,:), 'g-', 'LineWidth',1.2);hold on;
plot(time, X_est(2,:), 'b--', 'LineWidth',1.2);
legend('真实Y位置','UKF估计Y位置','Location','best');
xlabel('时间 / s');ylabel('Y 位置');grid on;

说明

  1. 系统模型：本程序定义了典型的非线性状态转移函数与非线性量测函数，可根据实际工程需求直接替换为目标系统的非线性模型，无需对滤波框架做修改。
  2. UKF 参数设置 ：程序中选取的 α = 1 e − 3 、 β = 2 、 κ = 0 \alpha=1e-3、\beta=2、\kappa=0 α=1e−3、β=2、κ=0为工程中的通用最优参数，适用于绝大多数高斯分布的滤波场景；如需适配特定分布，可微调参数取值。
  3. 滤波实现逻辑：程序严格遵循无迹卡尔曼滤波的标准流程，包含 Sigma 点生成、状态预测、量测预测、增益求解与状态更新全环节，代码可读性强且易于修改。
  4. 结果绘制：通过对比真实状态与滤波估计状态的时间序列曲线，可直观评估 UKF 的滤波精度与收敛性。

该程序为无迹卡尔曼滤波的通用实现模板，可直接移植至各类非线性状态估计场景，具备较强的工程参考价值。

via:

相关推荐
Evand J1 个月前
【matlabfilter例程】二维平面的雷达测角+测距目标跟踪，单个雷达，KF融合雷达和IMU数据。轨迹绘图、误差绘图输出。附代码下载链接
matlab·雷达·卡尔曼滤波·kf·跟踪·kalman·二维
Evand J2 个月前
【MATLAB例程】2雷达二维目标跟踪滤波系统-UKF（无迹卡尔曼滤波）实现，目标匀速运动模型（带扰动）。附代码下载链接
开发语言·matlab·目标跟踪·滤波·卡尔曼滤波
Evand J2 个月前
【MATLAB例程】二维平面上，三个雷达对一个目标跟踪，输出观测平均与UKF滤波两种算法的结果对比，附下载链接
matlab·平面·目标跟踪·滤波·卡尔曼滤波
jz_ddk2 个月前
[实战] 卡尔曼滤波原理与实现（GITHUB 优秀库解读）
算法·github·信号处理·kalman filter·卡尔曼滤波
Evand J2 个月前
【自适应粒子滤波MATLAB例程】Sage Husa自适应粒子滤波，用于克服初始Q和R不准确的问题，一维非线性滤波。附下载链接
开发语言·matlab·卡尔曼滤波·自适应滤波·非线性
Ai多利7 个月前
能上Nature封面的idea！强化学习+卡尔曼滤波
强化学习·卡尔曼滤波
大耳猫8 个月前
卡尔曼滤波算法简介与 Kotlin 实现
算法·kotlin·卡尔曼滤波
放羊郎9 个月前
卡尔曼滤波解释及示例
ekf·卡尔曼滤波·ukf·akf
Stara05119 个月前
YOLOv8+ Deepsort+Pyqt5车速检测系统
yolov8·pyqt5·卡尔曼滤波·deepsort
热门推荐
01GitHub 镜像站点02Labelme从安装到标注：零基础完整指南03Linux下V2Ray安装配置指南04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05jdk21下载、安装（Windows、Linux、macOS）06Claude Code 2.1.2 升级报错？别折腾了，一行命令搞定072025-04-03 Latex学习1——本地配置Latex + VScode环境08自用Proteus(8.15)常用元器件图示和功能介绍(持续更新...)09【踩坑笔记】50系显卡适配的 PyTorch 安装10Opencode CLI 安装成功,但是启动失败