【MATLAB程序，一维非线性EKF与RTS】MATLAB，用于一维的位移与速度滤波和RTS平滑/高精度定位，带滤波前后的误差对比

非线性动态系统下的扩展卡尔曼滤波（EKF）与 Rauch--Tung--Striebel（RTS）平滑算法的联合仿真与性能对比分析。
原创代码，请勿翻卖

程序简介

本代码演示了如何在一个具有非线性动力学 和非线性观测特征的系统中，通过两步法获取最优的状态估计：

前向过程 (EKF)： 在实时运行中，利用当前时刻的观测值动态更新位置和速度。
后向过程 (RTS 平滑)： 在获得所有数据后，利用未来的信息反向修正历史轨迹，进一步消除噪声，提高精度。

代码结构分解

模块名称	关键操作	目的
参数初始化	设置时间步长 `dt`、噪声协方差 `Q` 和 `R`。	定义仿真环境的物理特性与噪声强度。
数据生成	使用递归方程生成真实轨迹，并叠加随机噪声生成观测值 `z`。	模拟真实场景，作为滤波器的输入。
EKF 前向滤波	计算状态转移雅可比矩阵和观测雅可比。	解决非线性系统的实时线性化逼近。
RTS 后向平滑	从时刻反向计算到时刻，修正 EKF 的估计值。	利用"全局视角"显著降低 EKF 的滞后和随机误差。
结果评估	绘制位置、速度对比曲线及误差曲线，计算 RMSE。	直观展示平滑算法相较于基础 EKF 的性能提升。

算法优势与应用

高精度： 通过 RTS 平滑，代码展示了如何显著降低均方根误差 (RMSE)，尤其是在处理突变或高噪声数据时
非线性处理： 利用雅可比矩阵（Jacobian）实时线性化，是工程中处理复杂系统（如雷达跟踪、机器人导航）的通用手段
分析工具： 提供了完整的误差评估指标（RMSE 和标准差），方便直接用于数据分析

运行结果

运行结果有若干图片和命令行输出的误差统计特性。

位移的曲线和误差曲线如下：

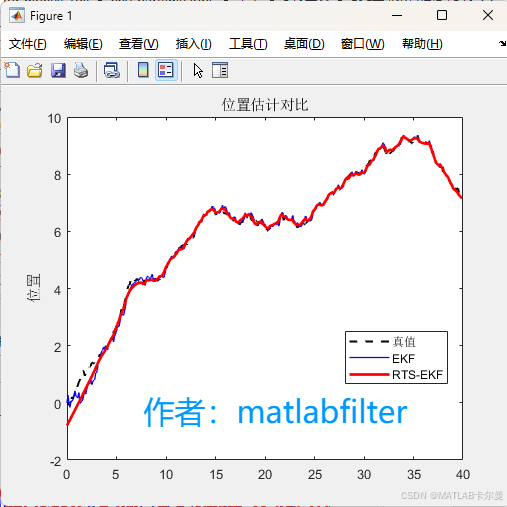
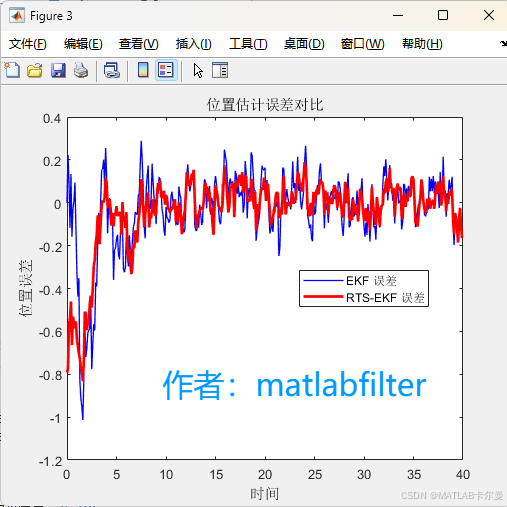
速度曲线和误差曲线如下：

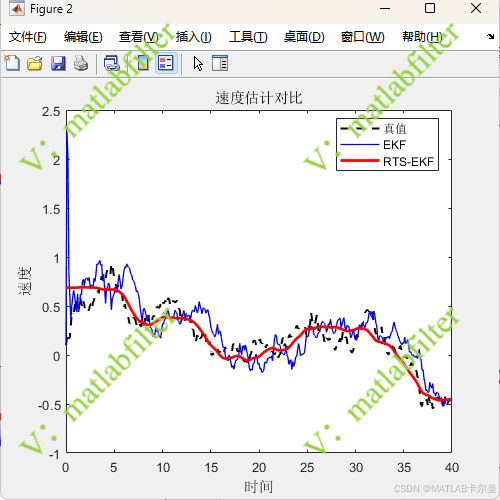
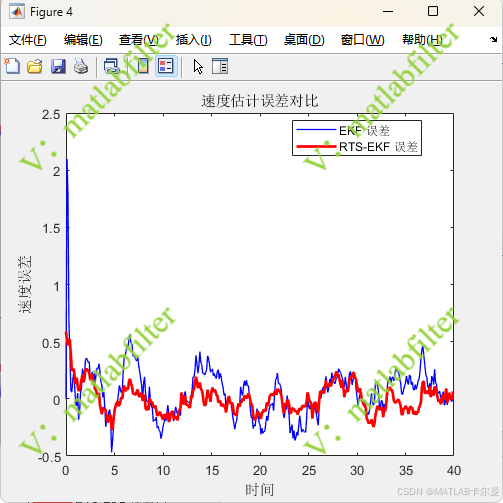
命令行截图：

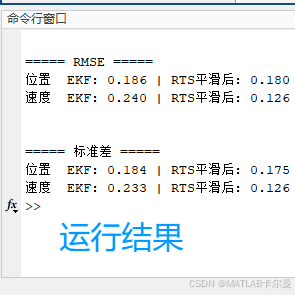
MATLAB源代码

部分代码如下：

matlab 复制代码

%% EKF + RTS 平滑（非线性系统）
% 状态：位置 + 速度
% 作者: matlabfilter（V同号，可接代码定制、讲解与调试）
% 2026-01-15/Ver1

clear; clc; close all;
rng(0);

%% ====参数设置
dt = 0.1;
T  = 40;
N  = T/dt;
t  = (0:N-1)*dt;
alpha = 1e-5;           % 非线性强度
Q = 0.001*diag([5, 2]);   % 过程噪声
R = 4;                  % 观测噪声

%% ======= 真实状态与观测
x_true = zeros(2,N);
x_true(:,1) = [0;0.1];
z = zeros(1,N);
for k = 2:N
    p = x_true(1,k-1);
    v = x_true(2,k-1);
    x_true(:,k) = [
        p + v*dt;
        v + alpha*sin(p)
    ] + mvnrnd([0;0],Q)';
end

完整代码：
如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者