2026年--Lc336-1448. 统计二叉树中好节点的数目(树）--java版

豆沙沙包?2026-01-11 11:04

1.题目

2.思路

时间复杂度：O(n)，其中 n 为二叉树中的节点个数。在深度优先遍历的过程中，每个节点只会被遍历一次。

空间复杂度：O(n)。由于我们使用递归来实现深度优先遍历，因此空间复杂度的消耗主要在栈空间，取决于二叉树的高度，最坏情况下二叉树的高度为 O(n)。

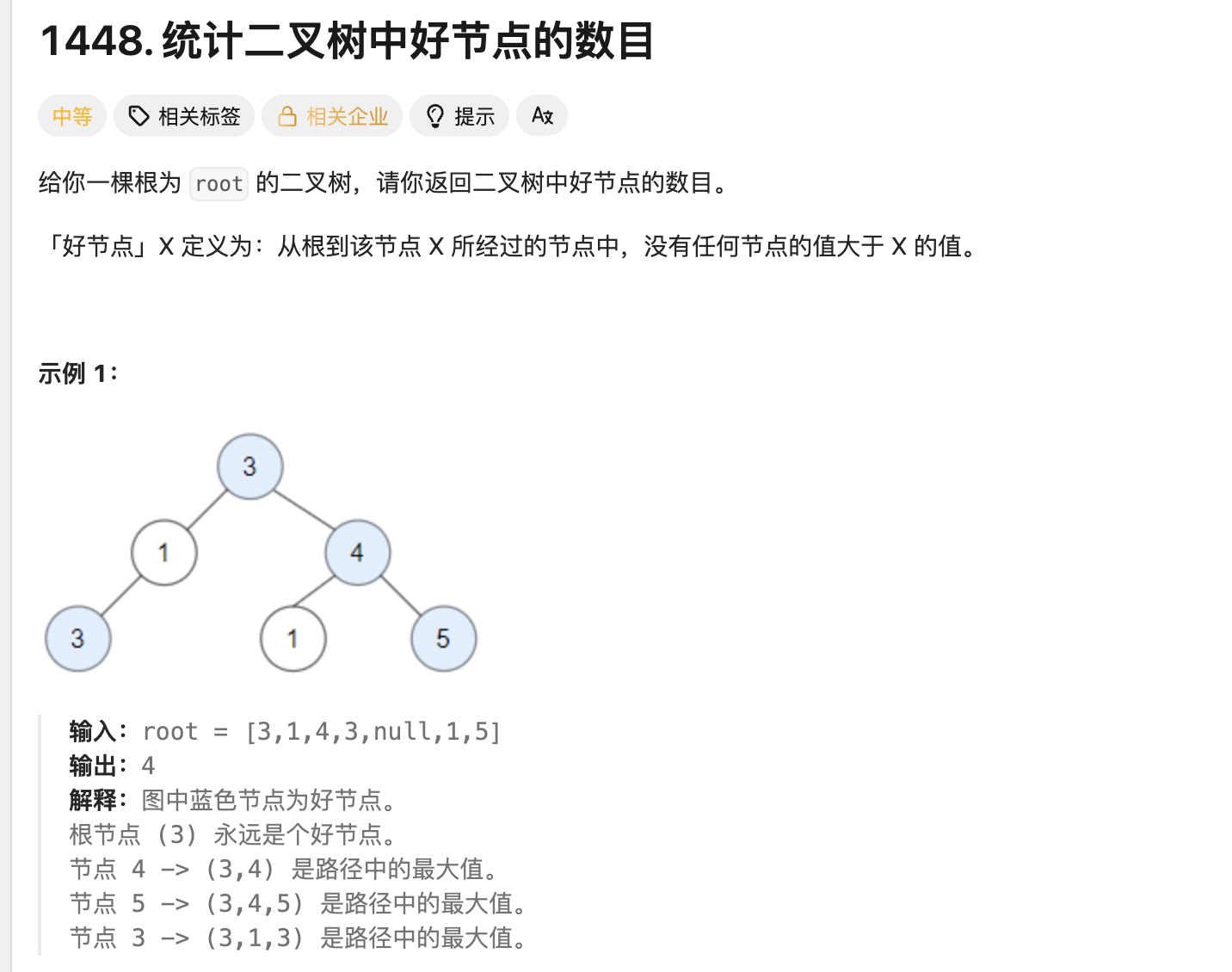
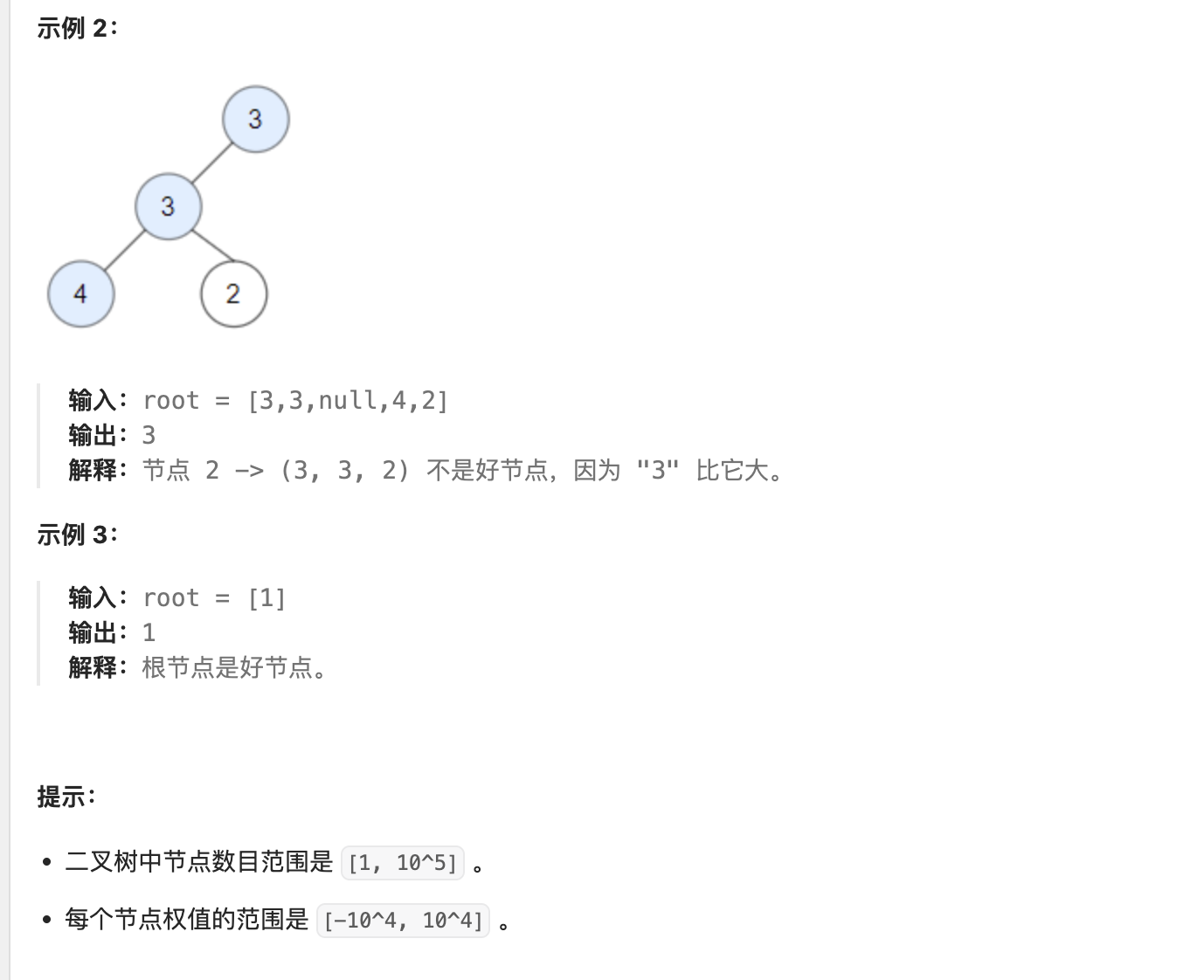
在题目的定义中，从根到好节点所经过的节点中，没有任何节点的值大于好节点的值，等同于根节点到好节点的路径上所有节点（不包括好节点本身）的最大值小于等于好节点的值。

可以在深度优先遍历的过程中，记录从根节点到当前节点的路径上所有节点的最大值，若当前节点的值大于等于该最大值，则认为当前节点是好节点。

3.代码实现

java 复制代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int goodNodes(TreeNode root) {
        if(root.left==null&&root.right==null)
        {
            return 1;
        }else if(root==null)
        {
            return 0;
        }else{
            return dfs(root,Integer.MIN_VALUE);
        } 
    }
    public int dfs(TreeNode root,int pathMax)
    {
        if(root==null)
        {
            return 0;
        }
        int res=0;
        if(root.val>=pathMax)
        {
            pathMax=root.val;
            res++;//计数器➕1
        }
        //递归遍历左右子树
        res=res+dfs(root.left,pathMax)+dfs(root.right,pathMax);
        return res;
    }
}