rate3775...题目其实很有意义,这样的一个几何题在游戏引擎相关的开发中非常有用,各种光线、模型求交的时候都需要有这样的几何思考能力。
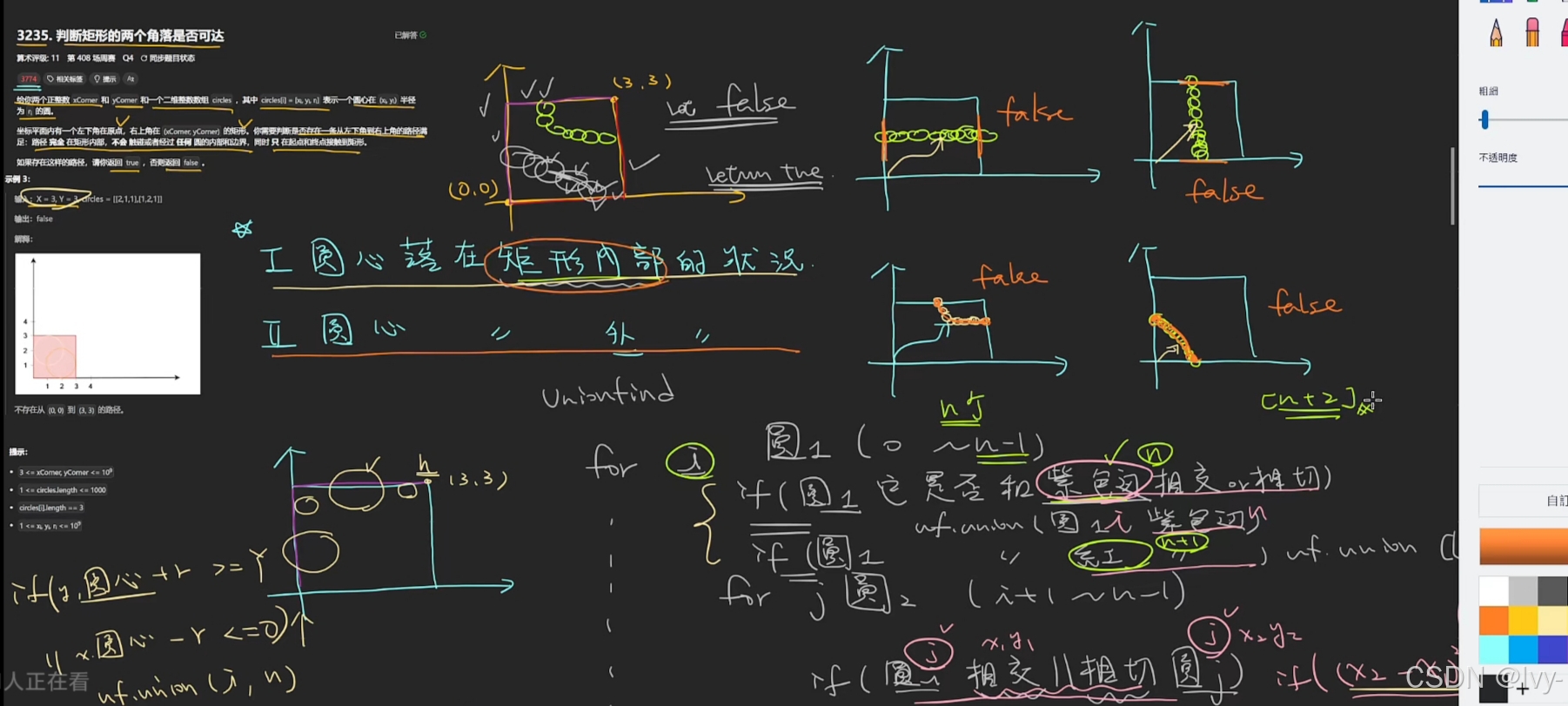
lc3235
DFS遍历相交的圆,判断是否存在圆阻碍矩形左下角到右上角的路径
若圆包含矩形顶点或形成左/上边界到右/下边界的阻碍链则返回false,否则返回true
class Solution {
// 判断点 (x,y) 是否在圆 (ox,oy,r) 内
bool in_circle(long long ox, long long oy, long long r, long long x, long long y) {
return (ox - x) * (ox - x) + (oy - y) * (oy - y) <= r * r;
}
public:
bool canReachCorner(int X, int Y, vector<vector<int>>& circles) {
int n = circles.size();
vector<int> vis(n);
auto dfs = [&](auto&& dfs, int i) -> bool {
long long x1 = circles[i][0], y1 = circles[i][1], r1 = circles[i][2];
// 圆 i 是否与矩形右边界/下边界相交相切
if (y1 <= Y && abs(x1 - X) <= r1 || x1 <= X && y1 <= r1) {
return true;
}
vis[i] = true;
for (int j = 0; j < n; j++) {
long long x2 = circles[j][0], y2 = circles[j][1], r2 = circles[j][2];
// 在两圆相交相切的前提下,点 A 是否严格在矩形内
if (!vis[j] && (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) <= (r1 + r2) * (r1 + r2) &&
x1 * r2 + x2 * r1 < (r1 + r2) * X &&
y1 * r2 + y2 * r1 < (r1 + r2) * Y &&
dfs(dfs, j)) {
return true;
}
}
return false;
};
for (int i = 0; i < n; i++) {
long long x = circles[i][0], y = circles[i][1], r = circles[i][2];
if (in_circle(x, y, r, 0, 0) || // 圆 i 包含矩形左下角
in_circle(x, y, r, X, Y) || // 圆 i 包含矩形右上角
// 圆 i 是否与矩形上边界/左边界相交相切
!vis[i] && (x <= X && abs(y - Y) <= r || y <= Y && x <= r) && dfs(dfs, i)) {
return false;
}
}
return true;
}
};
java推论版
并查集过925/978 case
class UnionFind {
}
class Solution {
public boolean canReachCorner(int x, int y, int[][] a) {
int n = a.length;
// space: O(n);
// time:
UnionFind uf = new UnionFind(n + 2);
for(int i = 0; i < n; i++){
int[] p = a[i];
int x1 = p[0], y1 = p[1], r1 = p[2];
// 判断紫色边
if(x1 - r1 <= 0 || y1 + r1 >= y)
uf.union(i, n);
// 判断红色边
if(y1 - r1 <= 0 || x1 + r1 >= x)
uf.union(i, n + 1);
for(int j = i + 1; j < n; j++){
int[] q = a[j];
int x2 = q[0], y2 = q[1], r2 = q[2];
if((long)(x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1) <= (long)(r2 + r1) * (r2 + r1)){
uf.union(i, j);
}
}
}
if(uf.isUnion(n, n + 1))
return false;
return true;
}
}
dfs check ac
- inCircle 方法:判断点是否在圆内,避免浮点运算,用平方和比较。
- dfs 方法:深搜相连的圆,判断是否能从左/上边界 连通到右/下边界
- canReachCorner 主方法:初始化变量后,遍历每个圆,若包含矩形顶点则直接返回 false ;
若与左/上边界相交则启动DFS,若DFS返回 true (连通右/下边界)则返回 false ,否则最终返回 true 。
class Solution {
int X;
int Y;
int[][] a;
boolean[] vis;
int n;
long x, y, r; // 用于inCircle方法的临时变量
// 判断点(targetX, targetY)是否在圆(x,y,r)内(包括边界)
private boolean inCircle(long x, long y, long r, long targetX, long targetY) {
return (targetX - x) * (targetX - x) + (targetY - y) * (targetY - y) <= r * r;
}
// DFS遍历相连的圆,判断是否能从左/上边界连通到右/下边界
private boolean dfs(int i) {
long x1 = a[i][0], y1 = a[i][1], r1 = a[i][2];
// 判断是否连通到右/下边界
if (y1 <= Y && Math.abs(X - x1) <= r1 ||
x1 <= X && y1 - 0 <= r1 ||
x1 > X && inCircle(x1, y1, r1, X, 0)) {
return true;
}
vis[i] = true;
// 遍历所有其他圆,判断是否相交/相切且交集在矩形内
for (int j = 0; j < n; j++) {
if (i == j || vis[j]) continue;
long x2 = a[j][0], y2 = a[j][1], r2 = a[j][2];
// 两圆相交/相切 且 交集在矩形内的条件
if ((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) <= (r1 + r2) * (r1 + r2) &&
r1 * y2 + r2 * y1 < (r1 + r2) * Y &&
r1 * x2 + r2 * x1 < (r1 + r2) * X) {
if (dfs(j)) {
return true;
}
}
}
return false;
}
public boolean canReachCorner(int X, int Y, int[][] a) {
this.X = X;
this.Y = Y;
this.a = a;
this.n = a.length;
this.vis = new boolean[n];
for (int i = 0; i < n; i++) {
long x = a[i][0], y = a[i][1], r = a[i][2];
// 若圆包含起点(0,0)或终点(X,Y),直接不可达
if (inCircle(x, y, r, 0, 0) || inCircle(x, y, r, X, Y))
return false;
// 若圆与左/上边界相交且未访问,DFS判断是否连通到右/下边界
if (!vis[i] && (x <= X && Math.abs(y - Y) <= r ||
y <= Y && x - 0 <= r ||
y > Y && inCircle(x, y, r, 0, Y))) {
if (dfs(i)) {
return false;
}
}
}
return true;
}
};