Part8_编写自己的解释器

今天，我们将谈一谈一元操作符：正号（+）和负号（-）操作符。

今天的很多内容都以之前文章中的内容为基础。所以，如果你需要简单回顾一下，请移步到Part7。记住：复习是学习之母。

下面就是你今天将要学习的内容：

扩展你的语法规则，使其能够处理正号、负号操作符。
添加一个新的AST节点类：UnaryOp。
扩展你的语法解析器，使其能够生成一棵含有UnaryOp类型节点的AST。
扩展你的解释器，添加一个新的方法：visit_UnaryOp ，用于解释AST中的UnaryOp类型的节点。

让我们开始吧，准备好了吗？

迄今为止，我们只涉及到了二元操作符^[1](#1)（+、-、*、/）。

那么，一元操作符是什么呢？一元操作符 是仅仅操作一个操作数的操作符。

下面列出了正号和负号操作符的具体规则：

负号操作符会生成其操作数的取反值。
正号操作符直接返回其操作数的值。
一元操作符要比二元操作符有更高的优先级。

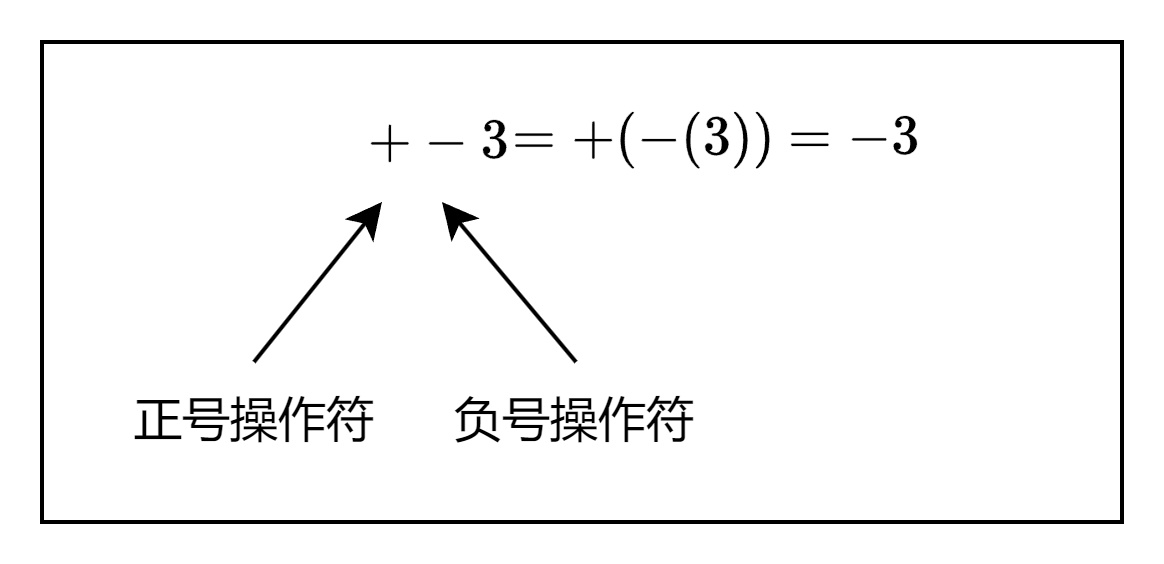
在表达式 " + − 3 " "+-3" "+−3"中，第一个 " + " "+" "+"操作符是正号操作符，第二个 " − " "-" "−"操作符是负号操作符。表达式 " + − 3 " "+-3" "+−3"和 " + ( − 3 ) " "+(-3)" "+(−3)"是等价的，最后的计算结果都是 − 3 -3 −3。你可以认为表达式中的 -3 是一个负的整数值，但是我们将其看作对正整数3的取反：

看看另一个表达式 " 5 − − 2 " "5--2" "5−−2":

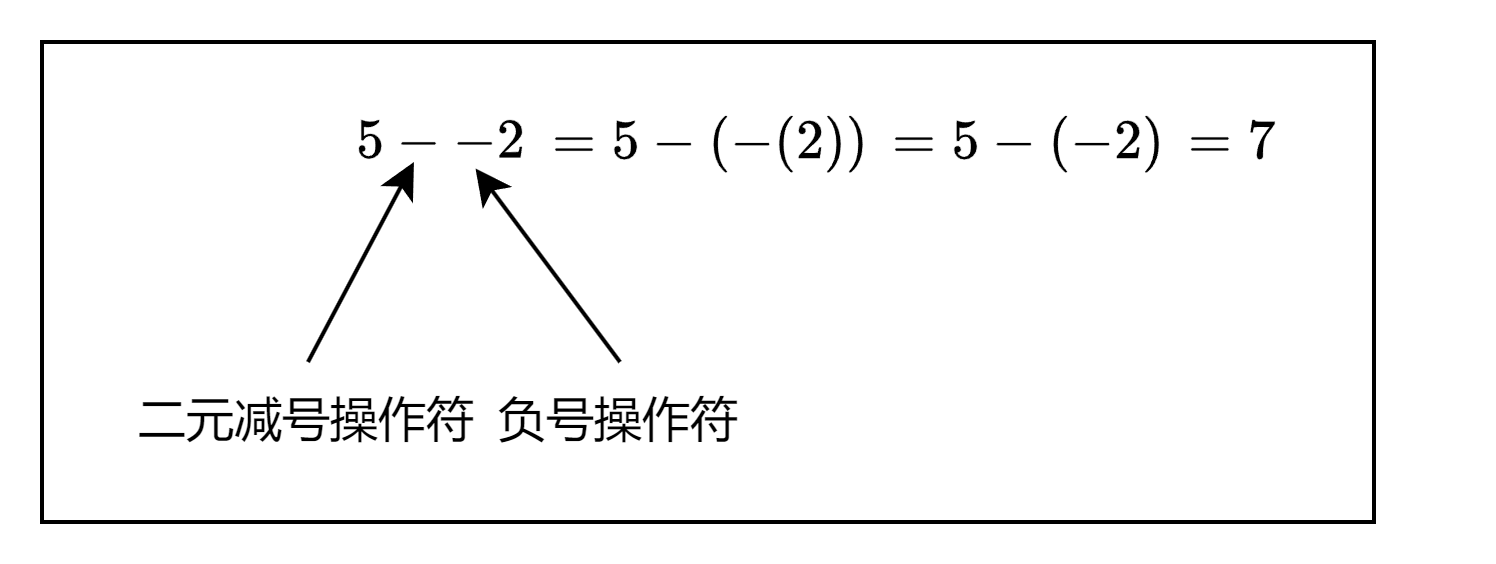
在表达式 " 5 − − 2 " "5--2" "5−−2"中，第一个 " − " "-" "−"代表二元的相减操作，第二个 " − " "-" "−"代表一元的取反操作。

更多的例子如下：

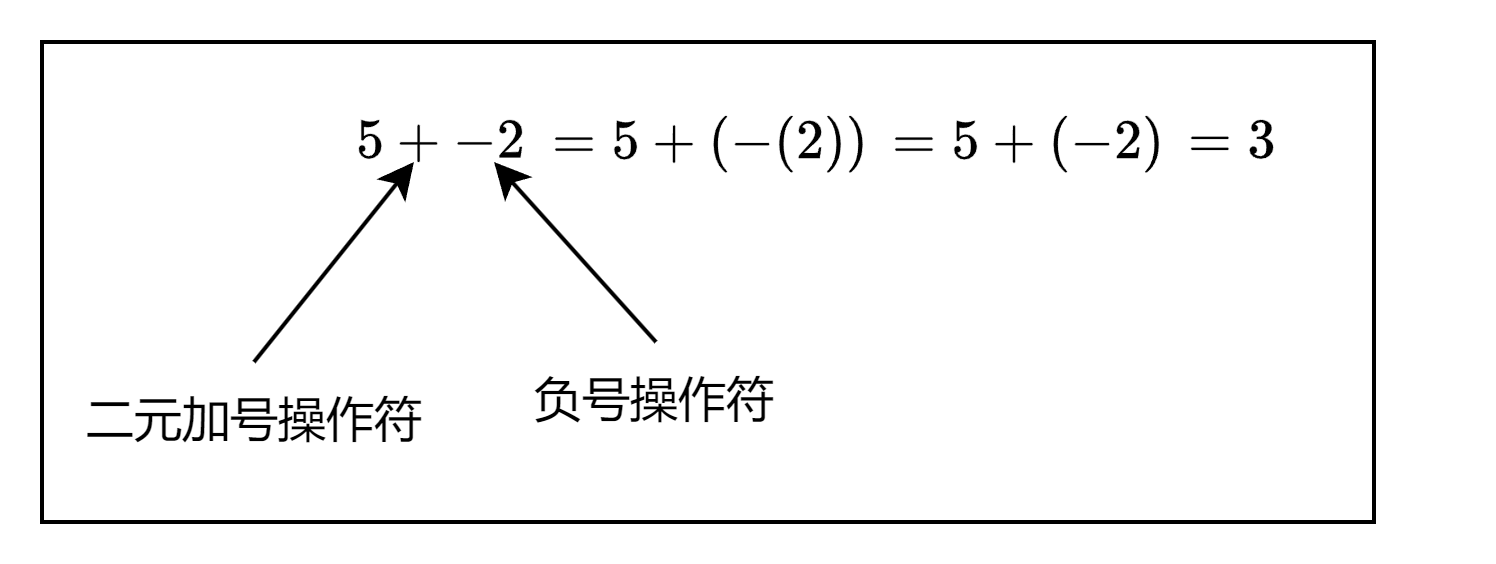
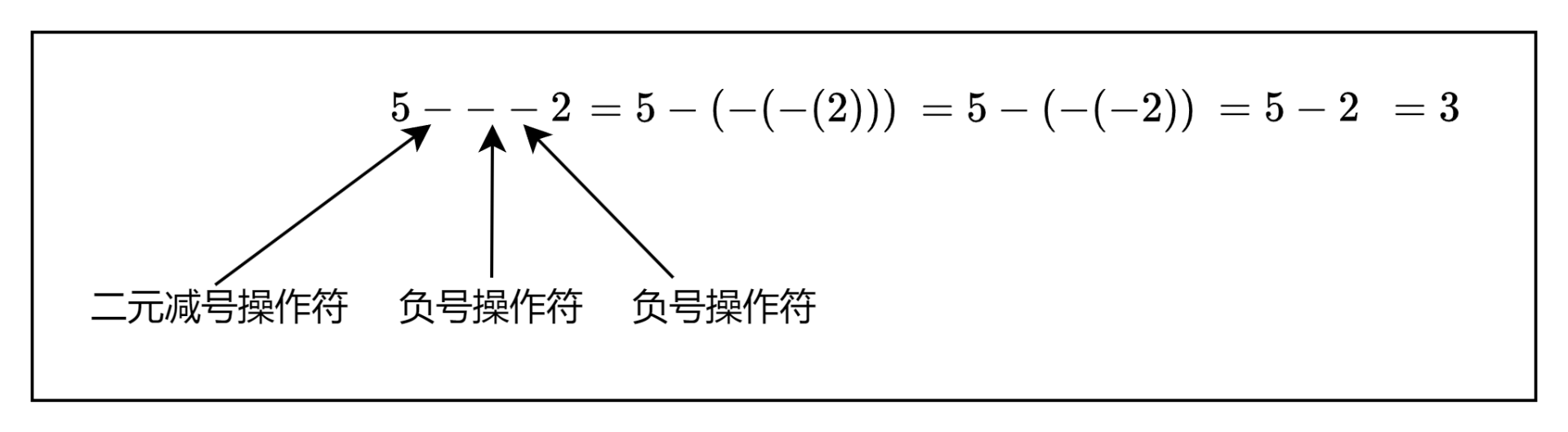
是时候更新我的语法规则了，使其能够支持一元正号操作符和一元负号操作符。我们将会修改factor规则，在其中添加对一元操作符的支持，这是因为一元的操作符的优先级要高于二元操作符。

我们当前的factor 规则是：

修改后的 factor 规则是：

如你所见，我让factor 规则引用了它自己，使得其能够推导含有大量一元操作符的合法表达式，比如： " − − − + − 3 " "- - - + - 3" "−−−+−3"。

下面就是能够支持含有一元正号运算符和一元负号运算符表达式的完整BNF:

下一步，就是添加一个用于表示一元操作符的AST节点类：

python 复制代码

class UnaryOp(AST):

    def __init__(
            self,
            op: Token,
            operand: AST
    ):
        super().__init__(op)
        self.op = op
        self.operand = operand

构造方法接受两个参数：op 代表一元操作符的符号实例对象（正号或者负号）；operand代表一个AST节点。

我们更新后的语法规则中，变化的内容在factor 规则中，因此我们将会修改语法解析器中的factor 方法。我们将在方法中添加一些代码，使其能够处理 (PLUS|MINUS)factor 规则：

python 复制代码

def factor(self) -> AST:
    """
    factor: (PLUS|MINUS)factor | INTEGER | LPAREN expr RPAREN
    :return 算数表达式的计算值
    """
    token: Token = self.current_token

    if token.type == INTEGER:
        self.eat(INTEGER)
        return Num(token)
    elif token.type == LPAREN:
        self.eat(LPAREN)
        node: AST = self.expr()
        self.eat(RPAREN)
        return node
    elif token.type == PLUS:
        self.eat(PLUS)
        return UnaryOp(token, self.factor())
    else:
        self.eat(MINUS)
        return UnaryOp(token, self.factor())

现在，我们就该去修改解释器 的代码了。我们要添加一个visit_UnaryOp方法，使其能够解释一元操作符节点：

python 复制代码

def visit_UnaryOp(self, node: UnaryOp) -> int:
    if node.token.type == PLUS:
        return self.visit(node.operand)
    else:
        return -self.visit(node.operand)

继续！

让我们来手动构建表达式 " 5 − − − 2 " "5---2" "5−−−2"的AST，并且将其传入到我们的解释器中去验证新添加的visit_UnaryOp方法可以正常工作。下面是我的验证结果：

python 复制代码

five_tok = Token(INTEGER, 5)
two_tok = Token(INTEGER, 2)
minus_tok = Token(MINUS, '-')
expr_node = BinOp(
	Num(five_tok),
	minus_tok,
	UnaryOp(minus_token, UnaryOp(minus_token, Num(two_tok)))
)
inter = Interpreter(None)
inter.visit(expr_node)
3

完整代码为：

python 复制代码

import abc
from typing import Callable

###############################################################################
#                                                                             #
#  词法解析器                                                                   #
#                                                                             #
###############################################################################

"""
    符号类型
    EOF(end-of-file)符号用于表示在词法分析中没有更多的输入
"""
INTEGER, PLUS, MINUS, MUL, DIV, LPAREN, RPAREN, EOF = (
    'INTEGER',
    'PLUS',
    'MINUS',
    'MUL',
    'DIV',
    'LPAREN',
    'RPAREN',
    'EOF'
)

class Token:

    def __init__(
            self,
            type: str,
            value: int | str | None
    ):
        """
        :param type: 符号类型：INTEGER（整数）、PLUS（加号）、MINUS（减号）、MUL（乘号）、DIV(除号)、LPAREN（左括号）、RPAREN（右括号）、EOF
        :param value: 0-9 | '+' | '-' | '*' | '/' | '(' | ')' | None
        """
        self.type = type
        self.value = value

    def __str__(self) -> str:
        """
        Token实例的字符串表示。

        例子：
            Token(INTEGER, 3)
            Token(PLUS, '+')
            Token(MINUS, '-')
            Token(MUL, '*')
            Token(DIV, '/')
            Token(LPAREN, '(')
            Token(RPAREN, ')')
            Token(EOF, None)
        :return:
        """
        return 'Token(type={type}, value={value})'.format(
            type=self.type,
            value=repr(self.value)
        )

    def __repr__(self) -> str: return self.__str__()

class Lexer:

    def __init__(
            self,
            text: str
    ):
        # 客户端的字符串输入："3 * 5"、"12 / 3 * 4"等等
        self.text = text
        # self.pos是self.text中字符的索引
        self.current_pos: int = 0
        self.current_char: str | None = self.text[self.current_pos]

    def error(self) -> None: raise Exception('非法字符')

    def advance(self) -> None:
        """
        自增self.pos使其指向下一个字符的索引以及设置self.current_char的值
        :return: None
        """
        self.current_pos += 1
        if self.current_pos > len(self.text) - 1:
            self.current_char = None  # 表示已经没有更多的输入字符用于解析符号实例
        else:
            self.current_char = self.text[self.current_pos]

    def skip_whitespace(self) -> None:
        while self.current_char is not None and self.current_char.isspace():
            self.advance()

    def integer(self) -> int:
        """
        返回text中连续多数位组成的整数值
        :return: 多数位整数值
        """
        result: str = '0'
        while self.current_char is not None and self.current_char.isdigit():
            result = f'{result}{self.current_char}'
            self.advance()
        return int(result)

    def get_next_token(self) -> Token:
        """
        词法解析器（也被称作扫描器或者符号序列化器）
        这个方法负责将输入的文本解析为一个个符号实例。每调用一次，解析一个符号实例。
        :return 符号实例
        """

        while self.current_char is not None:

            if self.current_char.isspace():
                self.skip_whitespace()

            if self.current_char.isdigit():
                return Token(INTEGER, self.integer())

            if self.current_char == '+':
                self.advance()
                return Token(PLUS, '+')

            if self.current_char == '-':
                self.advance()
                return Token(MINUS, '-')

            if self.current_char == '*':
                self.advance()
                return Token(MUL, '*')

            if self.current_char == '/':
                self.advance()
                return Token(DIV, '/')

            if self.current_char == '(':
                self.advance()
                return Token(LPAREN, '(')

            if self.current_char == ')':
                self.advance()
                return Token(RPAREN, ')')

            self.error()

        return Token(EOF, None)

###############################################################################
#                                                                             #
#  语法解析器                                                                   #
#                                                                             #
###############################################################################
class AST(abc.ABC):

    def __init__(self, token: Token):
        self.token = token


class BinOp(AST):

    def __init__(
            self,
            left: AST,
            op: Token,
            right: AST
    ):
        super().__init__(op)
        self.left = left
        self.op = op
        self.right = right

class UnaryOp(AST):

    def __init__(
            self,
            op: Token,
            operand: AST
    ):
        super().__init__(op)
        self.op = op
        self.operand = operand

class Num(AST):

    def __init__(self, value: Token):
        super().__init__(value)
        self.value: int = value.value

class Parser:

    def __init__(self, lexer: Lexer):
        self.lexer = lexer
        # 设置current_token的值为输入中的第一个符号
        self.current_token = lexer.get_next_token()

    def error(self) -> None: raise Exception('不合法的语法结构')

    def eat(self, token_type: str) -> None:
        """
        比较当前符号实例的符号类型和传入的符号类型是否一致：
            1. 一致："吃掉"当前符号实例，并且将下一个符号实例赋值给self.current_token；
            2. 不一致：抛出异常；
        :param token_type: 传入的符号类型
        """
        if self.current_token.type == token_type:
            self.current_token = self.lexer.get_next_token()
        else:
            self.error()

    def factor(self) -> AST:
        """
        factor: (PLUS|MINUS)factor | INTEGER | LPAREN expr RPAREN
        :return 算数表达式的计算值
        """
        token: Token = self.current_token

        if token.type == INTEGER:
            self.eat(INTEGER)
            return Num(token)
        elif token.type == LPAREN:
            self.eat(LPAREN)
            node: AST = self.expr()
            self.eat(RPAREN)
            return node
        elif token.type == PLUS:
            self.eat(PLUS)
            return UnaryOp(token, self.factor())
        else:
            self.eat(MINUS)
            return UnaryOp(token, self.factor())


    def term(self) -> AST:
        """
        term: factor((MUL|DIV)factor)*
        :return: 算数表达式的计算值
        """
        node: AST = self.factor()

        while self.current_token.type in (MUL, DIV):
            token: Token = self.current_token

            if token.type == MUL:
                self.eat(MUL)
            elif token.type == DIV:
                self.eat(DIV)

            node = BinOp(
                left=node,
                op=token,
                right=self.factor()
            )

        return node


    def expr(self) -> AST:
        """
        算数表达式的语法解析器/解释器

        calc> 7 + 3 * (10 / (12 / (3 + 1) - 1))
        22

        expr: term((PLUS|MINUS)term)*
        term: factor((MUL|DIV)factor)*
        factor: INTEGER | LPAREN expr RPAREN
        :return: 算数表达式的计算值
        """
        node: AST = self.term()

        while self.current_token.type in (PLUS, MINUS):
            token: Token = self.current_token

            if token.type == PLUS:
                self.eat(PLUS)
            elif token.type == MINUS:
                self.eat(MINUS)

            node = BinOp(
                left=node,
                op=token,
                right=self.factor()
            )

        return node

    def parse(self) -> AST: return self.expr()

###############################################################################
#                                                                             #
#  解释器                                                                      #
#                                                                             #
###############################################################################
class NodeVisitor(abc.ABC):

    def visit(self, node: AST) -> int | None:
        visitor: Callable[[AST], int | None] = getattr(self, f'visit_{type(node).__name__}', self.visit_generic)
        return visitor(node)

    def visit_generic(self, node: AST) -> None:
        raise Exception('未找到方法: visit_{name}'.format(name=type(node).__name__))

class Interpreter(NodeVisitor):

    def __init__(self, parser: Parser):
        self.parser = parser

    def visit_BinOp(self, node: BinOp) -> int:
        if node.token.type == PLUS:
            return self.visit(node.left) + self.visit(node.right)
        elif node.token.type == MINUS:
            return self.visit(node.left) - self.visit(node.right)
        elif node.token.type == MUL:
            return self.visit(node.left) * self.visit(node.right)
        else:
            return self.visit(node.left) // self.visit(node.right)

    def visit_Num(self, node: Num) -> int:
        return node.value

    def visit_UnaryOp(self, node: UnaryOp) -> int:
        if node.token.type == PLUS:
            return self.visit(node.operand)
        else:
            return -self.visit(node.operand)

    def interpret(self) -> int:
        tree: AST = self.parser.parse()
        return self.visit(tree)

def main():
    while True:
        try:
            try:
                text = input('calc> ')
            except NameError:  # Python3
                text = input('calc> ')
        except EOFError:
            break
        if not text:
            continue

        lexer = Lexer(text)
        parser = Parser(lexer)
        interpreter = Interpreter(parser)
        result = interpreter.interpret()
        print(result)


if __name__ == '__main__':
    main()

保存上面的代码，运行它。看看基于AST的解释器能否正确的计算含有一元操作符的算术表达式。

下面是在我的笔记本上运行的例子：

bash 复制代码

calc> - 3
-3
calc>  + 3
3
calc> 5 - - - + - 3
8
calc> 5 - - - + - (3 + 4) - +2
10
calc>

二元操作符：操作两个操作数的操作符。 ↩︎