源码:https://github.com/Illusionna/tiny-stats/blob/main/auto_ttest.c
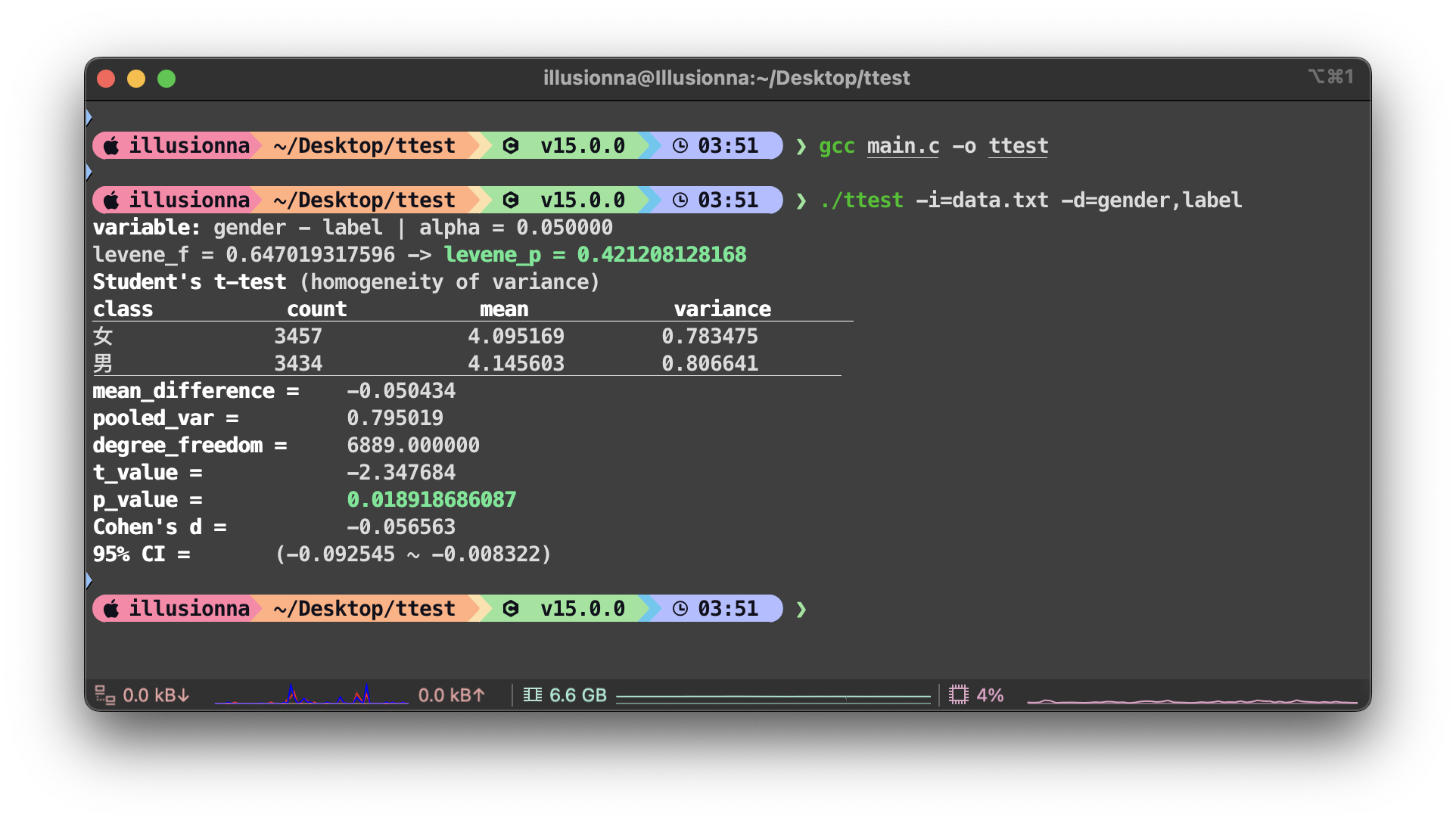
data.txt 数据集样例,检验维度是 gender 和 label 两个变量,首先进行 Levene 方差齐性检验,然后再决定是 Student T 检验(样本量需要足够大,否则要满足正态性)还是 Welch T 检验:
cpp
gender b01 b11 label
女 是 有 5
男 是 有 5
男 不是 有 4
女 是 有 3
女 是 有 5
cpp
/*
gcc -O2 auto_ttest.c -o ttest -lm
./ttest -i=data.txt -d=gender,label
*/
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct {
double *samples;
int n;
double mean;
double var;
} Group;
typedef struct {
double f;
double f_p_value;
int equal_var;
double t;
double df;
double p;
double diff;
double cohen;
double pooled_var;
double ci_upper;
double ci_lower;
} Indicator;
double random_normal(double mu, double sigma) {
static double U;
static double V;
static int phase = 0;
double Z;
if (phase == 0) {
U = (rand() + 1.0) / (RAND_MAX + 1.0);
V = (rand() + 1.0) / (RAND_MAX + 1.0);
Z = sqrt(-2.0 * log(U)) * sin(2.0 * M_PI * V);
} else {
Z = sqrt(-2.0 * log(U)) * cos(2.0 * M_PI * V);
}
phase = 1 - phase;
return Z * sigma + mu;
}
int compare_number(const void *a, const void *b) {
double diff = *(double *)a - *(double *)b;
return (diff > 0) - (diff < 0);
}
double median(double *data, int n) {
double *cache = (double *)malloc(n * sizeof(double));
for (int i = 0; i < n; i++) cache[i] = data[i];
qsort(cache, n, sizeof(double), compare_number);
double result;
if (n % 2 == 0) result = (cache[n / 2 - 1] + cache[n / 2]) / 2.0;
else result = cache[n / 2];
free(cache);
return result;
}
double levene_f(double *group1, double *group2, int n1, int n2) {
int N = n1 + n2;
double **Z = (double **)malloc(2 * sizeof(double *));
double *group_means_Z = (double *)malloc(2 * sizeof(double));
double grand_mean_Z = 0;
double mid;
mid = median(group1, n1);
Z[0] = (double *)malloc(n1 * sizeof(double));
double sum_Z0 = 0.0;
for (int i = 0; i < n1; i++) {
Z[0][i] = fabs(group1[i] - mid);
sum_Z0 = sum_Z0 + Z[0][i];
}
group_means_Z[0] = sum_Z0 / n1;
grand_mean_Z = grand_mean_Z + sum_Z0;
mid = median(group2, n2);
Z[1] = (double *)malloc(n2 * sizeof(double));
double sum_Z1 = 0.0;
for (int i = 0; i < n2; i++) {
Z[1][i] = fabs(group2[i] - mid);
sum_Z1 = sum_Z1 + Z[1][i];
}
group_means_Z[1] = sum_Z1 / n2;
grand_mean_Z = grand_mean_Z + sum_Z1;
grand_mean_Z = grand_mean_Z / N;
double ssb = 0.0;
double ssw = 0.0;
ssb = ssb + n1 * pow(group_means_Z[0] - grand_mean_Z, 2);
for (int i = 0; i < n1; i++) ssw = ssw + pow(Z[0][i] - group_means_Z[0], 2);
ssb = ssb + n2 * pow(group_means_Z[1] - grand_mean_Z, 2);
for (int i = 0; i < n2; i++) ssw = ssw + pow(Z[1][i] - group_means_Z[1], 2);
double msb = ssb / (2 - 1);
double msw = ssw / (N - 2);
double f = msb / msw;
for (int i = 0; i < 2; i++) free(Z[i]);
free(Z);
free(group_means_Z);
return f;
}
double incbeta(double a, double b, double x) {
static const double epsilon = 1.0e-30;
static const double condition = 1.0e-12;
if (x < 0.0 || x > 1.0) return INFINITY;
if (x > (a + 1.0) / (a + b + 2.0)) return 1.0 - incbeta(b, a, 1.0 - x);
double f = 1.0;
double c = 1.0;
double d = 0.0;
const double lbeta_ab = lgamma(a) + lgamma(b) - lgamma(a + b);
const double front = exp(a * log(x) + b * log(1.0 - x) - lbeta_ab) / a;
for (int i = 0; i <= 200; ++i) {
int m = i / 2;
double numerator;
if (i == 0) numerator = 1.0;
else if (i % 2 == 0) numerator = (m * (b - m) * x) / ((a + 2.0 * m - 1.0) * (a + 2.0 * m));
else numerator = - ((a + m) * (a + b + m) * x) / ((a + 2.0 * m) * (a + 2.0 * m + 1));
d = 1.0 + numerator * d;
if (fabs(d) < epsilon) d = epsilon;
d = 1.0 / d;
c = 1.0 + numerator / c;
if (fabs(c) < epsilon) c = epsilon;
double cd = c * d;
f = f * cd;
if (fabs(1.0 - cd) < condition) return front * (f - 1.0);
}
return INFINITY;
}
double ppf_normal_approx(double p) {
if (p < 0.5) return -ppf_normal_approx(1.0 - p);
double c0 = 2.515517;
double c1 = 0.802853;
double c2 = 0.010328;
double d1 = 1.432788;
double d2 = 0.189269;
double d3 = 0.001308;
double t = sqrt(-2.0 * log(1.0 - p));
return t - ((c2 * t + c1) * t + c0) / (((d3 * t + d2) * t + d1) * t + 1.0);
}
double cornish_fisher(double p, double df) {
double z = ppf_normal_approx(p);
if (isinf(df)) return z;
double t = z + (pow(z, 3) + z) / (4.0 * df);
if (df < 32) t = t + (5.0 * pow(z, 5) + 16.0 * pow(z, 3) + 3.0 * z) / (96.0 * df * df);
return t;
}
double cdf_student_t(double t, double df) {
if (df <= 0.0) return NAN;
if (t == 0.0) return 0.5;
double cache = sqrt(t * t + df);
return incbeta(df / 2.0, df / 2.0, (t + cache) / (2.0 * cache));
}
double pdf_student_t(double t, double df) {
double lbeta_half = lgamma(df / 2.0) + lgamma(0.5) - lgamma((df + 1.0) / 2.0);
return exp(-lbeta_half) * pow(1.0 + (t * t) / df, -(df + 1.0) / 2.0) / sqrt(df);
}
double ppf_student_t(double p, double df) {
if (p <= 0.0) return -INFINITY;
if (p >= 1.0) return INFINITY;
if (p == 0.5) return 0.0;
if (df < 1.0) return NAN;
double epsilon = 1e-12;
int epochs = 100;
/*
double t = (p > 0.5) ? 1.0 : -1.0;
*/
double t = cornish_fisher(p, df);
for (int i = 0; i < epochs; i++) {
double cdf = cdf_student_t(t, df);
double pdf = pdf_student_t(t, df);
if (pdf < 1e-100) break;
// Newton-Raphson.
double delta = (cdf - p) / pdf;
t = t - delta;
if (fabs(delta) < epsilon) return t;
}
return t;
}
void ttest_levene(Indicator *indicator, double *g1, double *g2, int n1, int n2) {
double f = levene_f(g1, g2, n1, n2);
indicator->f = f;
if (f <= 0) {
indicator->f_p_value = 1.0;
} else {
double df1 = 2.0 - 1.0;
double df2 = (double)n1 + (double)n2 -2.0;
double x = df2 / (df2 + df1 * f);
indicator->f_p_value = incbeta(df2 / 2.0, df1 / 2.0, x);
}
}
void ttest_independent(Indicator *indicator, Group *group1, Group *group2, double alpha) {
ttest_levene(indicator, group1->samples, group2->samples, group1->n, group2->n);
if (indicator->f_p_value > alpha) indicator->equal_var = 1;
else indicator->equal_var = 0;
double t;
double df;
if (indicator->equal_var) {
df = group1->n + group2->n - 2.0;
double pooled_var = ((group1->n - 1.0) * group1->var + (group2->n - 1.0) * group2->var) / df;
t = (group1->mean - group2->mean) / sqrt(pooled_var * (1.0 / group1->n + 1.0 / group2->n));
} else {
double satterthwaite1 = group1->var / group1->n;
double satterthwaite2 = group2->var / group2->n;
t = (group1->mean - group2->mean) / sqrt(satterthwaite1 + satterthwaite2);
double numerator = (satterthwaite1 + satterthwaite2) * (satterthwaite1 + satterthwaite2);
double denominator = (satterthwaite1 * satterthwaite1) / (group1->n - 1.0) + (satterthwaite2 * satterthwaite2) / (group2->n - 1.0);
df = numerator / denominator;
}
double cdf = cdf_student_t(t, df);
double p = 2.0 * (cdf > 0.5 ? 1.0 - cdf : cdf);
double pooled_std = sqrt(((group1->n - 1) * group1->var + (group2->n - 1) * group2->var) / df);
double pooled_var = pooled_std * pooled_std;
double cohen = (group1->mean - group2->mean) / pooled_std;
double diff = group1->mean - group2->mean;
double se_diff = pooled_std * sqrt(1.0 / group1->n + 1.0 / group2->n);
double t_critical = ppf_student_t(1.0 - alpha / 2.0, df);
indicator->df = df;
indicator->t = t;
indicator->p = p;
indicator->diff = diff;
indicator->pooled_var = pooled_var;
indicator->cohen = cohen;
indicator->ci_lower = diff - t_critical * se_diff;
indicator->ci_upper = diff + t_critical * se_diff;
}
double ttest_paired(double *state1, double *state2, int n) {
if (n < 2) return NAN;
double sum_diff = 0.0;
double sum_square_diff = 0.0;
for (int i = 0; i < n; ++i) {
double diff = state1[i] - state2[i];
sum_diff = sum_diff + diff;
sum_square_diff = sum_square_diff + diff * diff;
}
double mean_diff = sum_diff / n;
double var_diff = (sum_square_diff - (sum_diff * sum_diff / n)) / (n - 1);
double std_error = sqrt(var_diff / n);
double t = mean_diff / std_error;
double cdf = cdf_student_t(t, n - 1.0);
double p = 2.0 * (cdf > 0.5 ? 1.0 - cdf : cdf);
return p;
}
void statistics(Group *group) {
double sum = 0.0;
double var = 0.0;
for (int i = 0; i < group->n; ++i) sum = sum + group->samples[i];
double mean = sum / group->n;
for (int i = 0; i < group->n; ++i) var = var + (group->samples[i] - mean) * (group->samples[i] - mean);
group->var = var / (group->n - 1);
group->mean = mean;
}
int read_file(char *path, char *X, char *Y, Group *group1, Group *group2, char **categories) {
FILE *f = fopen(path, "r");
if (!f) return 1;
char buffer[1024];
int count;
int idx = -1;
int idy = -1;
const char *delimiters = " \t\r\n";
if (fgets(buffer, sizeof(buffer), f)) {
char *token = strtok(buffer, delimiters);
int n;
for (n = 0; token != NULL; n++, token = strtok(NULL, delimiters)) {
if (strcmp(token, X) == 0) idx = n;
if (strcmp(token, Y) == 0) idy = n;
}
count = n;
}
if (idx == -1 || idy == -1) return 2;
int capacity1 = 64;
int capacity2 = 64;
group1->samples = (double *)malloc(capacity1 * sizeof(double));
group2->samples = (double *)malloc(capacity2 * sizeof(double));
group1->n = 0;
group2->n = 0;
int classification = 0;
while (fgets(buffer, sizeof(buffer), f)) {
int n;
char *x = NULL;
char *y = NULL;
char *token = strtok(buffer, delimiters);
for (n = 0; token != NULL; n++, token = strtok(NULL, delimiters)) {
if (n == idx) x = token;
if (n == idy) y = token;
}
if (count != n) return 3;
int group_id = -1;
for (int i = 0; i < classification; i++) {
if (strcmp(x , categories[i]) == 0) group_id = i;
}
if (group_id == -1) {
if (classification >= 2) {
fclose(f);
return 4;
}
categories[classification] = strdup(x);
group_id = classification++;
}
if (group_id == 0) {
if (group1->n >= capacity1) {
capacity1 = capacity1 * 2;
group1->samples = (double *)realloc(group1->samples, capacity1 * sizeof(double));
}
group1->samples[group1->n++] = atof(y);
}
if (group_id == 1) {
if (group2->n >= capacity2) {
capacity2 = capacity2 * 2;
group2->samples = (double *)realloc(group2->samples, capacity2 * sizeof(double));
}
group2->samples[group2->n++] = atof(y);
}
}
fclose(f);
return 0;
}
void print_ttest(char *X, char *Y, char **categories, Group *group1, Group *group2) {
double alpha = 0.05;
Indicator indicator;
statistics(group1);
statistics(group2);
ttest_independent(&indicator, group1, group2, alpha);
printf("\x1b[1mvariable:\x1b[0m %s - %s | alpha = %lf\n", X, Y, alpha);
printf("levene_f = %.12lf -> \x1b[1m\x1b[32mlevene_p = %.12lf\x1b[0m\n", indicator.f, indicator.f_p_value);
if (indicator.equal_var == 1) printf("\x1b[1mStudent's t-test\x1b[0m (homogeneity of variance)\n");
else printf("\x1b[1mWelch's t-test\x1b[0m (heterogeneity of variance)\n");
printf("\x1b[1m\x1b[4m%-15s %-15s %-15s %-15s\x1b[0m\n", "class", "count", "mean", "variance");
printf("%-15s %-15d %-15lf %-15lf\n", categories[0], group1->n, group1->mean, group1->var);
printf("\x1b[4m%-15s %-15d %-15lf %-15lf\x1b[0m\n", categories[1], group2->n, group2->mean, group2->var);
printf("\x1b[1mmean_difference =\x1b[0m %lf\n", indicator.diff);
printf("\x1b[1mpooled_var =\x1b[0m\t %lf\n", indicator.pooled_var);
printf("\x1b[1mdegree_freedom =\x1b[0m %lf\n", indicator.df);
printf("\x1b[1mt_value =\x1b[0m\t %lf\n", indicator.t);
printf("\x1b[1mp_value =\x1b[0m\t \x1b[1m\x1b[32m%.12lf\x1b[0m\n", indicator.p);
printf("\x1b[1mCohen's d =\x1b[0m\t %lf\n", indicator.cohen);
printf("\x1b[1m95%% CI =\x1b[0m (%lf ~ %lf)\n", indicator.ci_lower, indicator.ci_upper);
}
int main(int argc, char *argv[], char *envs[]) {
char path[256];
char X[64] = {0};
char Y[64] = {0};
if (argc == 1) {
fprintf(stderr, "\x1b[32m(Usage) >>>\x1b[0m %s -i=<filepath> -d=<dim1>,<dim2>\n", argv[0]);
return 1;
}
for (int i = 1; i < argc; i++) {
if (strncmp(argv[i], "-i=", 3) == 0) strcpy(path, argv[i] + 3);
else if (strncmp(argv[i], "-d=", 3) == 0) {
char buffer[256];
strncpy(buffer, argv[i] + 3, sizeof(buffer));
char *token = strtok(buffer, ",");
if (token != NULL) strcpy(X, token);
token = strtok(NULL, ",");
if (token != NULL) strcpy(Y, token);
}
else {
fprintf(stderr, "\x1b[31m[Error]\x1b[0m invalid parameter \"%s\"\n", argv[i]);
fprintf(stderr, "\x1b[32m(Usage) >>>\x1b[0m %s -i=<filepath> -d=<dim1>,<dim2>\n", argv[0]);
return 1;
}
}
char *categories[2] = {NULL, NULL};
Group *group1 = (Group *)malloc(sizeof(Group));
Group *group2 = (Group *)malloc(sizeof(Group));
int status = read_file(path, X, Y, group1, group2, categories);
switch (status) {
case 1:
printf("\x1b[31m[Error]\x1b[0m can not find the dataset file.\n");
goto release;
case 2:
printf("\x1b[31m[Error]\x1b[0m \"%s\" or \"%s\" is not in the table header.\n", X, Y);
goto release;
case 3:
printf("\x1b[31m[Error]\x1b[0m data is not aligned.\n");
goto release;
case 4:
printf("\x1b[31m[Error]\x1b[0m independent variable \"%s\" is not binary (more than 2 categories).\n", X);
goto release;
default:
break;
}
print_ttest(X, Y, categories, group1, group2);
release:
free(group1->samples);
free(group2->samples);
free(group1);
free(group2);
free(categories[0]);
free(categories[1]);
return 0;
}