学习初衷
最近萌生了自学AI 的念头,一个原因是确实对于AI 的原理及运行机制比较感兴趣,二是随着AI 发展,越来越多的行业开始拥抱AI,也希望通过学习AI 来进一步将其应用到自己的日常工作中。
学习计划
在初步阶段,打算跟随吴恩达老师的课程来复习一下所需的基本数学知识,并了解机器学习中一些基本概念和基本算法,课程和资料均可以通过blibli 进行搜索。
机器学习中的基本概念知识
机器学习,顾名思义为机器自我学习。在传统的软件中一般都需要coder 编写固定的代码,当程序运行时会根据固定的代码逻辑来执行,程序本身不会根据运行结果来改进。但是在机器学习领域,程序可以根据训练集和代价函数来自我调整,最终可以得到契合训练集的模型,目前在机器学习中主要有两个比较重要的概念:监督学习(supervisied learning)和无监督学习(unsupervisied learning)
监督学习
监督学习就是训练集中既有输入也有输出:
比如说一个地区的房价和房子大小的数据集,对于 80 平的房子价格为100 万,对于 120 平的房子价格为 140 万,对于 150 平的房子价格为 200 万,也就是说对于数据集中的任何输入都有一个明确的输出可以参考。
再比如医院中恶性肿瘤发生的概率,该问题的输入可能不止一个,比如病人的年龄、肿瘤大小均为输入。输出也不和上一个问题一样为一个数值,而是一个bool值(是恶性肿瘤/不是恶性肿瘤)。
无监督学习
无监督学习的数据集中不存在输入和输出的关系:
比如对于很多新闻软件的归类功能,输入为很多新闻信息,使用无监督学习可以将数以千万条的新闻进行聚类,将某些比较相似的新闻归类到一起,这样我们在浏览新闻时只需要浏览我们感兴趣的那一类。
一个简单的例子(预测某地区房价)
使用"预测一个地区的房价问题"为例,进一步理解机器学习的运行机制。
模型
目标:使用数据集训练一个一次函数为模型来预测某地区房价
模型:
根据模型的方程可以看到其中存在两个参数和
,在开始阶段我们先简化模型令
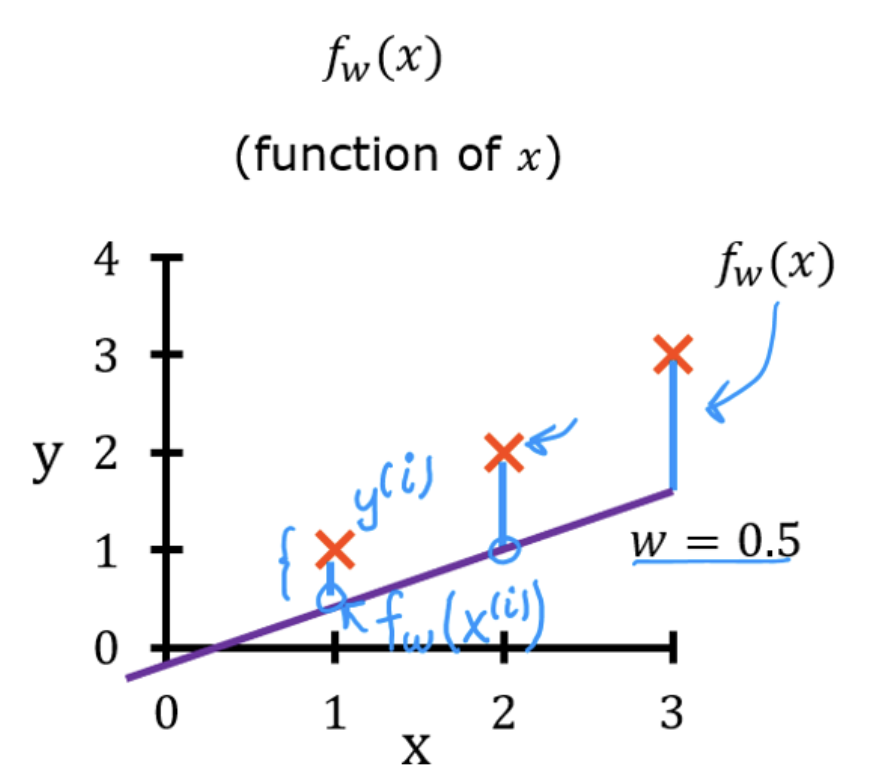
在机器学习中,需要一个代价函数来衡量当前模型的好坏,对于该问题来说,一个好的模型输入数据集中的输入值后应尽可能贴近数据集中的输出值。下图中❌为数据集中的数据,紫色直线为的图像,那在
时模型预测值和真实值的差值为|❌ -
|。一般数据集中不会只有一个数据,为了使代价函数更准确,我们一般使用方差来描述,即
其中为数据集的数量,
为使用模型预测的值,
为数据集中的真实值
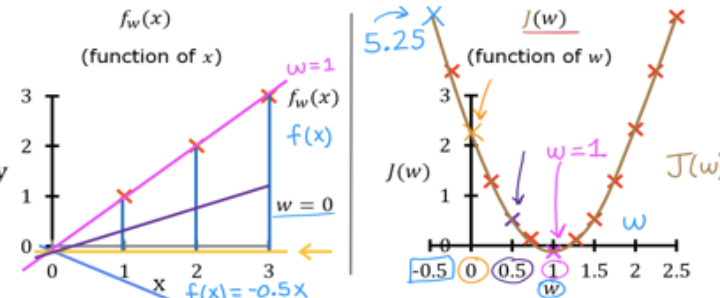
确定代价函数以后,需求就转变为通过数据集训练来实现代价函数最小,也就是使得我们的模型与数据集最贴合。我们可以先选择几个不同的取值,观察
在
取不同值时的变化趋势(这里我就直接给出了,运算也比较简单)。由图可见
为一个开口朝上的二次函数,其中在
时取得小值(同时也是最小值)。
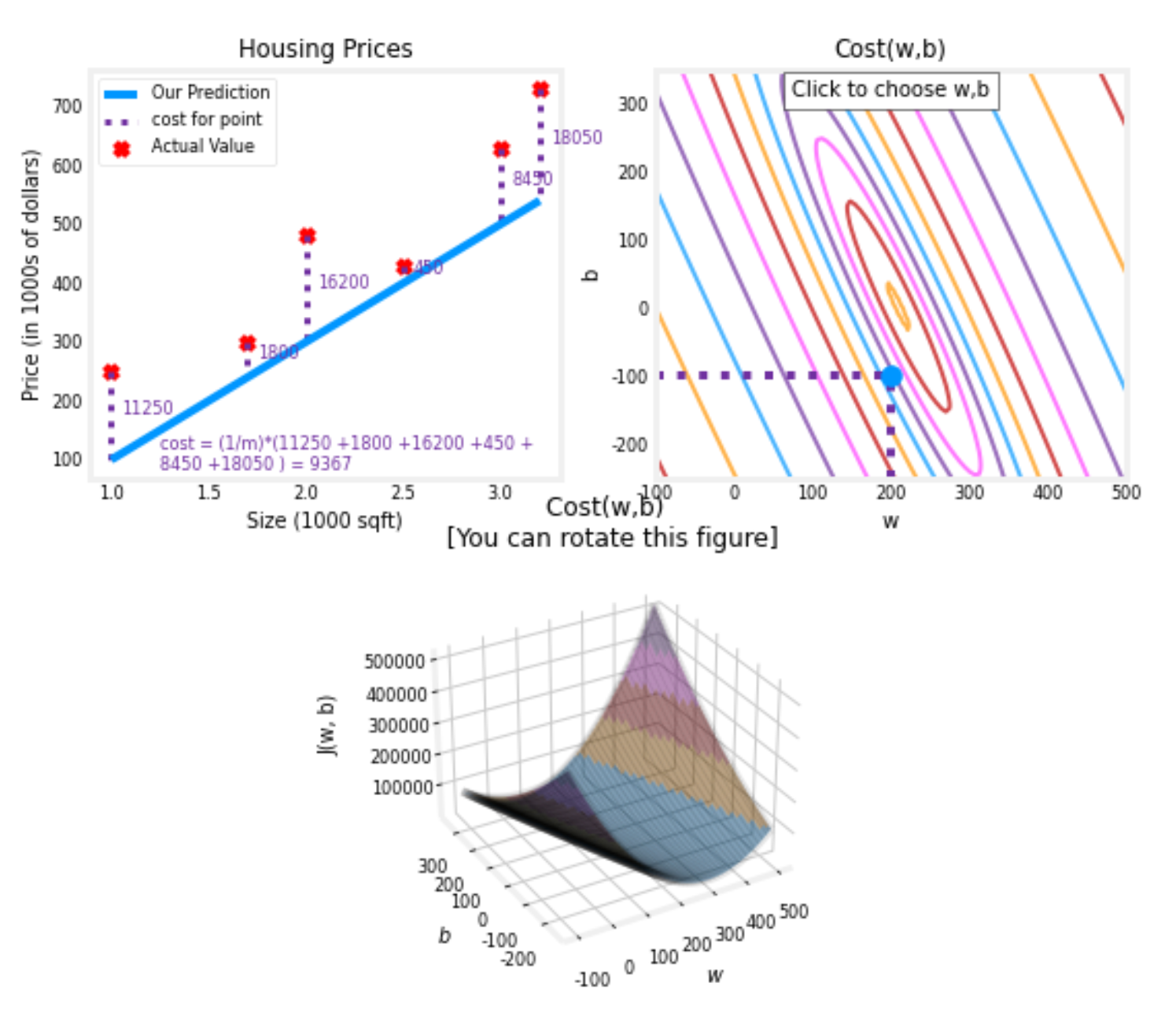
现在我们已经了解了在简化模型时代价随
的变化趋势,那我们需要在此基础上去掉
的假设,此时模型为
,该模型中不仅
会影响预测值,同样
的取值也会影响预测值。还是基于上述简化模型的做法,我们可以计算达到不同
和
的取值条件下代价函数得到的数值,不过不同于简化模型只有
一个参数,现在有
两个参数,所以新的代价函数
的图形如下所示,该函数图像为三维图像,可以描述在某个
取值情况下所对应的代价值。
梯度下降
在上面的讨论中我们已经得到了使用一次函数拟合某地区房价的模型,只是该模型的参数没有确定。在接触机器学习之前,我可能就会直接利用以前上学学的数值分析中的方法进行解决,使用已有的曲线拟合算法(最小二乘法、牛顿迭代法等)来直接得到最终函数,但这种方法属于coder在代码中直接告诉程序怎么做,无法通过训练集来进一步提升模型准确度,让我们看一下在机器学习中这类问题怎么解决。
简化模型
在简化代价函数中只有一个变量
,在训练过程中更新
的函数为:
其中为学习率,取值为0-1的小数,若
取值越小,则更新
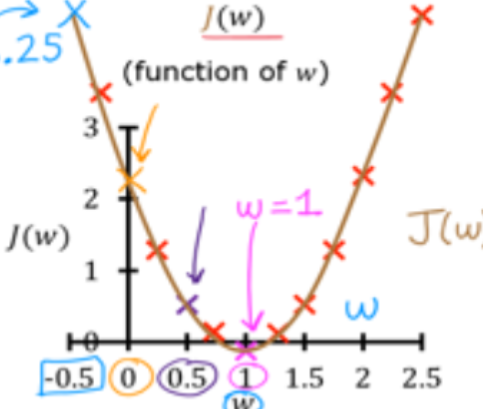
策略的步长越小。让我们看一下为什么这样做可以使得代价变小,再次拿出
函数图像,当
时导数为负数,使用
得到的
大于原始
,表示在图像中也就是向右移动,该移动会使
取值减小,满足我们预期。再比如当
时,此时导数为正数,新的
小于原始
,表现在图像中为向左移,同样会使得
减小。若
时,此时导数为0,
不再更新。但是需要注意的是学习率
也是一个重要参数,若取值过小,会使得程序性能降低,若取值过大,则不收敛。
最终模型
基于简化模型基本可以理解梯度下降算法的工作机制,但在最终模型中我们需要考虑两个变量,普通的函数导数已经不满足我们的需要,我们需要使用偏导数来执行梯度下降
偏导数
在单变量函数中"导数"描述了在某点处函数值
随自变量
的变化趋势,但是对于
这种存在不止一个变量的函数,我们就需要知道变量
在某点处分别对于函数值
变化趋势的影响。而偏导数就是可以用于描述该问题,对于函数
共有两个偏导,分别为
和
,对于偏导的求解属于基础知识就不展开了。
模型训练
在理解偏导数的概念以后,我们可以仿照简化模型的流程,根据当前处偏导数的正负来决定下一步
的取值,先写出我们代价函数的定义:
对于公式中为什么为,则是为了后续导数计算化简更为简洁,使用
也是没问题的
梯度的定义:
得到两个变量的偏导以后,则可以使用梯度下降来得到新一组的,总而实现模型的训练。下面贴图核心代码模块
python
def gradient_descent(x, y, w_init, b_init, alpha, iters, cost_func, grad_func):
"""
梯度下降优化算法
参数:
x (array): 输入特征
y (array): 目标值
w_init, b_init (float): 参数初始值
alpha (float): 学习率
iters (int): 迭代次数
cost_func: 代价函数
grad_func: 梯度计算函数
返回:
w, b (float): 优化后的参数
"""
w = w_init
b = b_init
for i in range(iters):
# 计算梯度
dw, db = grad_func(x, y, w, b)
# 更新参数
w -= alpha * dw
b -= alpha * db
return w, b