GDPO:英伟达提出多奖励强化学习的"解耦归一化"策略,解决GRPO的优势崩溃问题
一句话总结:NVIDIA 提出 GDPO(Group reward-Decoupled Normalization Policy Optimization),通过对每个奖励信号单独进行组内归一化后再聚合,解决了 GRPO 在多奖励场景下的"优势崩溃"问题,在工具调用、数学推理、代码推理三大任务上全面超越 GRPO。
📖 目录
- 引言:为什么多奖励强化学习会"翻车"?
- [问题剖析:GRPO 的优势崩溃现象](#问题剖析:GRPO 的优势崩溃现象)
- [GDPO 方法详解:解耦归一化的三步走策略](#GDPO 方法详解:解耦归一化的三步走策略)
- 奖励优先级优化:条件奖励设计
- [实验验证:三大任务全面超越 GRPO](#实验验证:三大任务全面超越 GRPO)
- [代码实现:从 GRPO 到 GDPO 的简单改造](#代码实现:从 GRPO 到 GDPO 的简单改造)
- 深度思考与启示
- 总结与展望
1. 引言:为什么多奖励强化学习会"翻车"?
1.1 从单一奖励到多奖励的演进
随着大语言模型(LLM)能力的不断提升,用户对模型的期望也越来越高。我们不仅希望模型能给出正确的答案,还希望它能:
- 📝 遵守特定格式(如 JSON、Markdown、特定标签)
- 📏 控制输出长度(不要太长也不要太短)
- 🐛 避免运行时错误(代码能正常执行)
- 🎯 满足多种偏好(安全、有帮助、诚实等)
这就引出了**多奖励强化学习(Multi-reward RL)**的需求------用多个奖励信号同时引导模型学习。
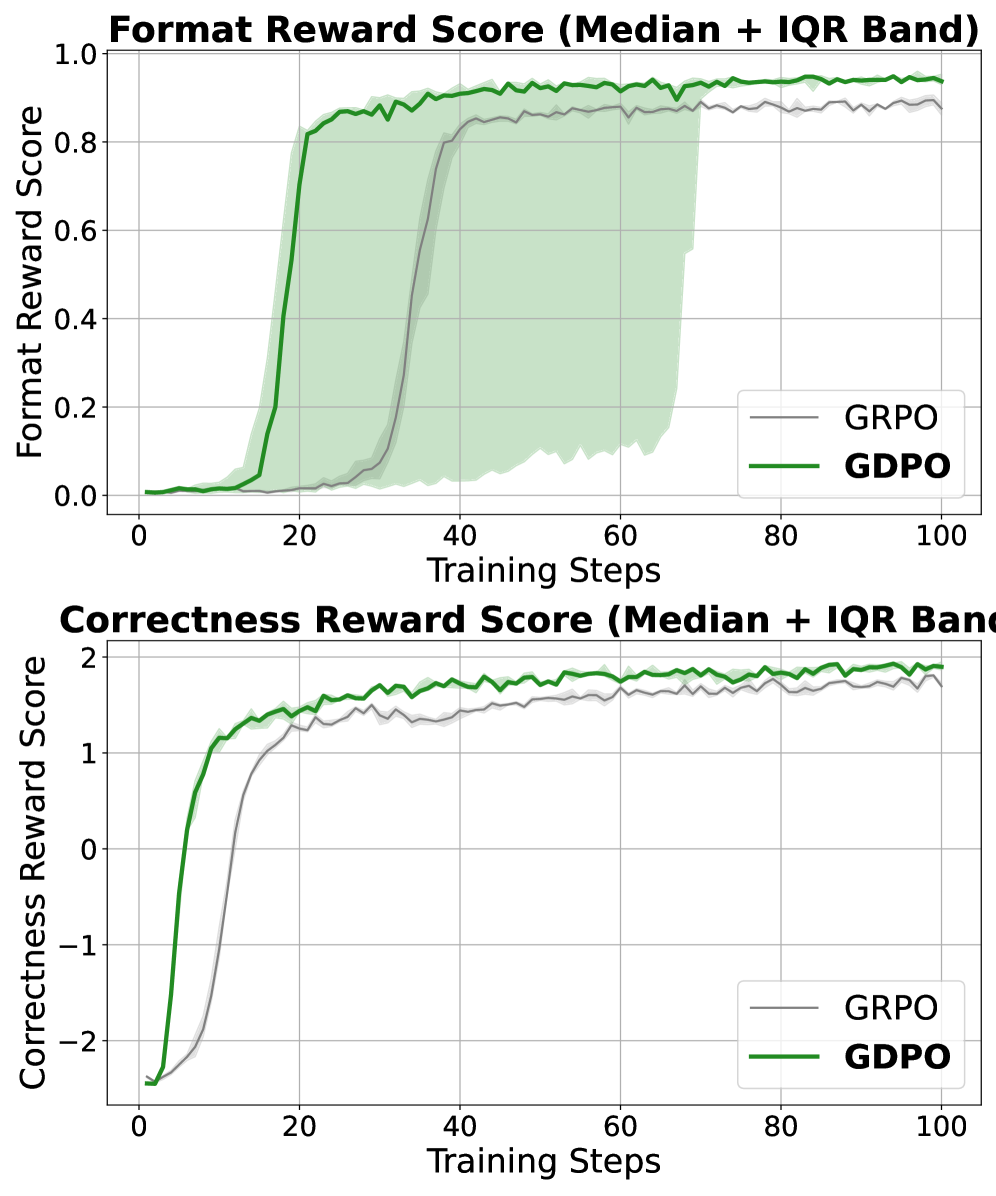
图1:(a) GDPO 方法概览------对每个奖励分别进行组内归一化,然后聚合并进行批次级归一化以保持数值稳定;(b) Qwen2.5-Instruct-1.5B 工具调用任务的奖励曲线对比,GDPO 在正确性和格式奖励上均收敛到更高分数。
1.2 当前主流做法的问题
目前最流行的做法是使用 GRPO(Group Relative Policy Optimization) 算法。GRPO 是 DeepSeek 团队在 2024 年提出的高效强化学习算法,核心思想是:
- 对同一个问题生成多个候选答案(rollout)
- 通过组内奖励的相对比较来计算优势值
- 无需训练额外的价值网络(Critic),大幅降低计算成本
但问题来了 :当我们有多个奖励信号时,通常的做法是直接把它们加起来,然后用 GRPO 处理。这看起来很自然,但 NVIDIA 的研究团队发现,这种做法会导致一个严重的问题------优势崩溃(Advantage Collapse)。
2. 问题剖析:GRPO 的优势崩溃现象
2.1 什么是优势崩溃?
让我们用一个生活化的比喻来理解这个问题。
想象你是一位老师,需要同时评价学生的数学成绩 和语文成绩。现在有两个学生:
- 小明:数学 90 分,语文 60 分,总分 150 分
- 小红:数学 60 分,语文 90 分,总分 150 分
如果你只看总分,这两个学生是"一样好"的。但实际上,他们的能力结构完全不同!如果你想培养数学人才,应该更看重小明;如果你想培养文科人才,应该更看重小红。
这就是 GRPO 在多奖励场景下的问题:它把不同的奖励组合"压扁"成了相同的优势值,丢失了关键的区分信息。
2.2 数学上的问题分析
让我们看看具体的数学公式。假设我们有两个奖励 r 1 r_1 r1 和 r 2 r_2 r2,GRPO 的做法是:
第一步:求和
r sum ( i , j ) = r 1 ( i , j ) + r 2 ( i , j ) r_{\text{sum}}^{(i,j)} = r_1^{(i,j)} + r_2^{(i,j)} rsum(i,j)=r1(i,j)+r2(i,j)
第二步:组内归一化
A sum ( i , j ) = r sum ( i , j ) − mean { r sum } std { r sum } A_{\text{sum}}^{(i,j)} = \frac{r_{\text{sum}}^{(i,j)} - \text{mean}\{r_{\text{sum}}\}}{\text{std}\{r_{\text{sum}}\}} Asum(i,j)=std{rsum}rsum(i,j)−mean{rsum}
问题在于,当我们先求和再归一化时,不同的奖励组合可能会得到相同的优势值。
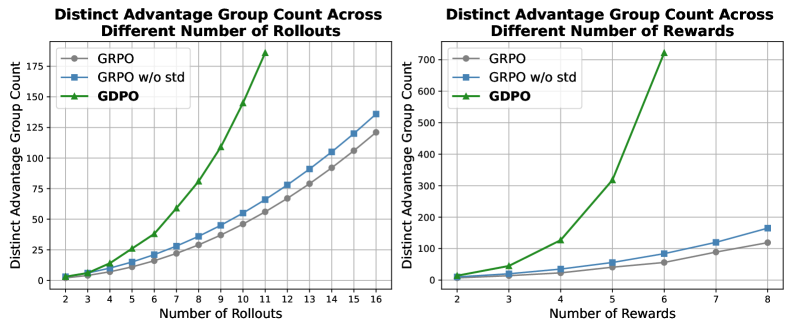
图2:二进制奖励场景下 GRPO 和 GDPO 的优势计算对比。GRPO 将不同奖励组合映射到仅两个优势组,而 GDPO 对每个奖励独立归一化后保留了三个不同的优势组。
2.3 一个具体的例子
假设我们有 4 个 rollout,每个都有两个二进制奖励(0 或 1):
| Rollout | r 1 r_1 r1 | r 2 r_2 r2 | r sum r_{\text{sum}} rsum |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 |
| 4 | 1 | 1 | 2 |
用 GRPO 的方法:
- 均值 = (0+1+1+2)/4 = 1
- 标准差 = 0.816
- Rollout 2 和 Rollout 3 的优势值 = (1-1)/0.816 = 0
问题 :Rollout 2(只满足 r 2 r_2 r2)和 Rollout 3(只满足 r 1 r_1 r1)被认为是"一样好"的,但如果 r 1 r_1 r1 是正确性奖励、 r 2 r_2 r2 是格式奖励,这两者的重要性可能完全不同!
2.4 优势组数量的可视化分析
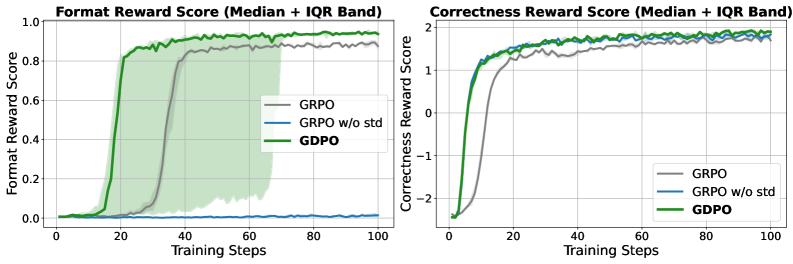
图3:GRPO、GRPO w/o std 和 GDPO 产生的不同优势组数量对比。随着 rollout 数量(左)或奖励数量(右)增加,GDPO 始终保留更多的优势组,提供更具表达力的训练信号。
从图3可以清楚地看到:
- GRPO(蓝色):产生的不同优势组数量最少,区分度最低
- GRPO w/o std(橙色):去掉标准差归一化后稍有改善
- GDPO(绿色):产生的不同优势组数量最多,区分度最高
3. GDPO 方法详解:解耦归一化的三步走策略
3.1 核心思想:先分别归一化,再聚合
GDPO 的核心创新非常简洁:不要先求和再归一化,而是先对每个奖励单独归一化,再求和。
这就像评价学生时,先把数学成绩和语文成绩各自转换成班级排名(归一化),再综合考虑,而不是直接看总分。
3.2 三步走策略
步骤1:单奖励组内归一化(解耦)
对每个奖励 r k r_k rk( k = 1 , . . . , n k=1,...,n k=1,...,n)单独进行组内归一化:
A k ( i , j ) = r k ( i , j ) − mean { r k ( i , 1 ) , . . . , r k ( i , G ) } std { r k ( i , 1 ) , . . . , r k ( i , G ) } A_k^{(i,j)} = \frac{r_k^{(i,j)} - \text{mean}\{r_k^{(i,1)}, ..., r_k^{(i,G)}\}}{\text{std}\{r_k^{(i,1)}, ..., r_k^{(i,G)}\}} Ak(i,j)=std{rk(i,1),...,rk(i,G)}rk(i,j)−mean{rk(i,1),...,rk(i,G)}
其中:
- ( i , j ) (i,j) (i,j) 表示第 i i i 个问题的第 j j j 个 rollout
- G G G 是每个问题的 rollout 数量
作用:
- 消除不同奖励的量纲差异(比如一个奖励范围是 0-1,另一个是 0-100)
- 保留每个奖励内部的相对优劣
- 避免某一个奖励主导整个优化过程
步骤2:多奖励优势求和
将所有归一化后的单奖励优势加权求和:
A sum ( i , j ) = w 1 ⋅ A 1 ( i , j ) + . . . + w n ⋅ A n ( i , j ) A_{\text{sum}}^{(i,j)} = w_1 \cdot A_1^{(i,j)} + ... + w_n \cdot A_n^{(i,j)} Asum(i,j)=w1⋅A1(i,j)+...+wn⋅An(i,j)
其中 w k w_k wk 是每个奖励的权重。
作用:融合多个目标的优化信号,此时每个目标的贡献已经通过步骤1进行了归一化处理。
步骤3:批次级优势归一化(稳定性保障)
对整个批次的优势值进行再次归一化:
A ^ sum ( i , j ) = A sum ( i , j ) − mean { A sum } std { A sum } + ϵ \hat{A}{\text{sum}}^{(i,j)} = \frac{A{\text{sum}}^{(i,j)} - \text{mean}\{A_{\text{sum}}\}}{\text{std}\{A_{\text{sum}}\} + \epsilon} A^sum(i,j)=std{Asum}+ϵAsum(i,j)−mean{Asum}
作用:
- 确保数值范围稳定,防止优势值随奖励数量增加而膨胀
- 实验表明,去掉这一步会导致偶尔的收敛失败
3.3 直观理解
让我们用一个更生活化的比喻来理解 GDPO:
想象你在招聘员工,需要同时考虑技术能力 和沟通能力:
GRPO 的做法(先求和再归一化):
- 给每个候选人的技术和沟通打分
- 直接把两个分数加起来
- 在所有候选人中比较总分
问题:如果技术分数范围是 0-100,沟通分数范围是 0-10,那技术分数会主导最终结果。
GDPO 的做法(先分别归一化再求和):
- 给每个候选人的技术和沟通打分
- 分别计算技术排名和沟通排名(归一化)
- 综合两个排名来评估
优势:每个维度的贡献是均衡的,不会因为分数范围不同而产生偏差。
4. 奖励优先级优化:条件奖励设计
4.1 问题:不同奖励的优化难度差异
在实际应用中,不同的奖励可能有不同的优化难度:
- 长度约束:相对容易满足(模型很快就能学会控制输出长度)
- 正确性:相对困难(需要真正理解问题才能给出正确答案)
如果简单地将两者相加,模型可能会"偷懒"------只优化容易的长度约束,而忽视困难的正确性。
4.2 解决方案:条件奖励
GDPO 提出了一种巧妙的解决方案------条件奖励(Conditioned Reward):
R ~ length = { R length if R correct ≥ t 0 otherwise \tilde{\mathcal{R}}{\text{length}} = \begin{cases} \mathcal{R}{\text{length}} & \text{if } \mathcal{R}_{\text{correct}} \geq t \\ 0 & \text{otherwise} \end{cases} R~length={Rlength0if Rcorrect≥totherwise
含义 :只有当正确性奖励达到阈值 t t t 时,才给予长度奖励。
效果:强制模型优先保证正确性,在正确的基础上再优化长度。
4.3 条件奖励的直观理解
这就像考试时的评分规则:
- 普通规则:答案正确得 60 分,书写工整得 40 分
- 条件规则:答案正确得 60 分;只有答案正确时,书写工整才额外得 40 分
第二种规则会促使学生优先保证答案正确,而不是花大量时间在书写上。
5. 实验验证:三大任务全面超越 GRPO
NVIDIA 团队在三个典型任务上验证了 GDPO 的效果:工具调用、数学推理、代码推理。
5.1 工具调用任务
任务描述 :训练模型学习如何调用外部工具,需要满足特定的输出格式(如 <tool_call> 和 <response> 标签)。
奖励设置:
- 格式奖励:检查输出结构是否正确
- 正确性奖励:评估工具调用的名称、参数是否匹配
实验结果:
| 方法 | 模型 | Live Acc | Multi-Turn Acc | Non-Live Acc | Avg Acc | Format |
|---|---|---|---|---|---|---|
| GRPO | Qwen2.5-1.5B | 59.73 | 56.43 | 72.04 | 62.73 | 98.25 |
| GDPO | Qwen2.5-1.5B | 62.50 | 59.01 | 73.85 | 65.12 | 99.38 |
| GRPO | Qwen2.5-3B | 65.27 | 59.50 | 80.14 | 68.30 | 99.00 |
| GDPO | Qwen2.5-3B | 67.12 | 61.39 | 80.95 | 69.82 | 99.63 |
表1:工具调用任务上 GDPO vs GRPO 的对比。GDPO 在所有指标上均优于 GRPO。
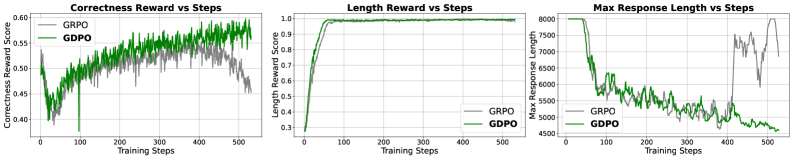
图4:Qwen2.5-1.5B 在工具调用任务上的训练曲线。GDPO 在正确性和格式奖励上均收敛到更高分数,而 GRPO w/o std 虽然正确性接近 GDPO,但格式奖励几乎没有提升。
关键发现:
- GDPO 在准确率上平均提升 2-3%
- 格式正确率接近 100%
- 训练过程更加稳定
5.2 数学推理任务
任务描述:解决高难度数学问题(AIME、AMC、MATH 等),同时遵守长度约束(响应长度 ≤ 4000 tokens)。
奖励设置:
- 长度奖励:检查响应长度是否合规
- 正确性奖励:检查最终答案是否正确
实验结果:
| 方法 | 模型 | AIME Acc | AMC Acc | MATH Acc | Exceed Rate |
|---|---|---|---|---|---|
| GRPO | DeepSeek-R1-1.5B | 35.0 | 62.5 | 85.7 | 11.3% |
| GDPO | DeepSeek-R1-1.5B | 39.2 | 67.5 | 87.2 | 4.8% |
| GRPO | DeepSeek-R1-7B | 51.7 | 75.0 | 91.2 | 8.7% |
| GDPO | DeepSeek-R1-7B | 55.0 | 77.5 | 92.1 | 3.2% |
表2:数学推理任务上 GDPO vs GRPO 的对比。GDPO 准确率更高,长度超出比例显著更低。
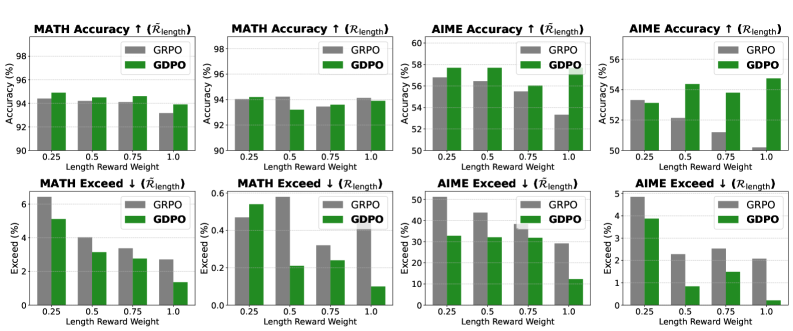
图5:DeepSeek-R1-1.5B 在数学推理任务上的训练行为。两者都快速最大化长度奖励,但 GDPO 随后恢复并超越 GRPO 的正确性。约 400 步后,GRPO 正确性下降且长度违规增加,而 GDPO 持续改善。
关键发现:
- GDPO 解决了 GRPO 在训练后期的正确性下降问题
- 长度超出比例降低了 50% 以上
- 在高难度问题(AIME)上提升最为明显
5.3 代码推理任务
任务描述:生成代码,需通过测试用例,遵守长度约束,且无运行时错误。
奖励设置:
- 通过率奖励:通过测试用例的比例
- 条件长度奖励:仅当代码正确且长度合规时给予奖励
- Bug 奖励:代码是否无编译或运行时错误
实验结果:
| 方法 | 奖励设置 | Apps | CodeContests | Codeforces | Taco | Exceed | Bug |
|---|---|---|---|---|---|---|---|
| GRPO | 2 rewards | 26.8 | 12.5 | 8.3 | 18.7 | 15.2% | 28.3% |
| GDPO | 2 rewards | 27.5 | 13.2 | 9.1 | 19.4 | 8.7% | 25.1% |
| GRPO | 3 rewards | 25.9 | 11.8 | 7.9 | 17.9 | 12.8% | 22.5% |
| GDPO | 3 rewards | 27.1 | 12.9 | 8.7 | 19.1 | 7.3% | 18.7% |
表3:代码推理任务上 GDPO vs GRPO 的对比。GDPO 在多目标平衡上表现更好。
关键发现:
- 在三奖励设置下,GDPO 表现出更好的多目标平衡能力
- Bug 比率降低了 15-20%
- 长度超出比例降低了 40% 以上
5.4 权重敏感性分析
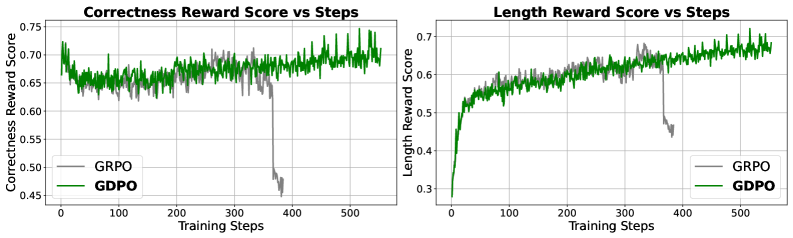
图6:DeepSeek-R1-7B 在不同长度奖励权重 {1.0, 0.75, 0.5, 0.25} 下的准确率和超长比例,对比了普通长度奖励与条件长度奖励的效果。
从图6可以看到:
- GRPO 对奖励权重非常敏感,权重选择不当会导致性能大幅下降
- GDPO 对权重变化更加鲁棒,在不同权重设置下都能保持较好的性能
5.5 条件奖励的效果
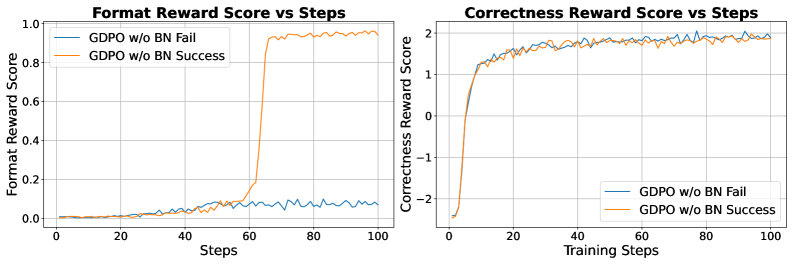
图7:DeepSeek-R1-7B 使用条件长度奖励时 GRPO 和 GDPO 的训练曲线。使用条件奖励后,训练初期没有剧烈的正确性下降,GDPO 在正确性恢复和提升上优于 GRPO。
使用条件奖励后:
- GDPO 能更有效地利用放松的长度约束来提升准确率
- GRPO 在条件奖励下仍然存在训练不稳定的问题
6. 代码实现:从 GRPO 到 GDPO 的简单改造
GDPO 的一大优势是实现简单,只需要对现有 GRPO 代码做少量修改。
6.1 GRPO 原始实现(TRL 框架)
python
# GRPO: 先聚合所有奖励
rewards = (rewards_per_func * self.reward_weights.to(device).unsqueeze(0)).nansum(dim=1)
# 计算组内均值和标准差
mean_grouped_rewards = rewards.view(-1, self.num_generations).mean(dim=1)
std_grouped_rewards = rewards.view(-1, self.num_generations).std(dim=1)
# 扩展到每个 rollout
mean_grouped_rewards = mean_grouped_rewards.repeat_interleave(self.num_generations, dim=0)
std_grouped_rewards = std_grouped_rewards.repeat_interleave(self.num_generations, dim=0)
# 归一化计算优势值
advantages = rewards - mean_grouped_rewards
if self.scale_rewards:
advantages = advantages / (std_grouped_rewards + 1e-4)6.2 GDPO 改进实现(TRL 框架)
python
# GDPO: 先对每个奖励单独归一化
rewards_per_func_filter = torch.nan_to_num(rewards_per_func)
all_reward_advantage = []
# 循环对每个奖励单独进行组内归一化
for i in range(len(self.reward_weights)):
reward_i = rewards_per_func_filter[:, i]
# 计算组内均值和标准差
each_reward_mean_grouped = reward_i.view(-1, self.num_generations).mean(dim=1)
each_reward_std_grouped = reward_i.view(-1, self.num_generations).std(dim=1)
# 扩展到每个 rollout
each_reward_mean_grouped = each_reward_mean_grouped.repeat_interleave(self.num_generations, dim=0)
each_reward_std_grouped = each_reward_std_grouped.repeat_interleave(self.num_generations, dim=0)
# 计算单个奖励的归一化优势
each_reward_advantage = reward_i - each_reward_mean_grouped
each_reward_advantage = each_reward_advantage / (each_reward_std_grouped + 1e-4)
all_reward_advantage.append(each_reward_advantage)
# 聚合所有归一化后的奖励
combined_reward_advantage = torch.stack(all_reward_advantage, dim=1)
pre_bn_advantages = (combined_reward_advantage * self.reward_weights.to(device).unsqueeze(0)).nansum(dim=1)
# 批次级归一化(稳定性保障)
bn_advantages_mean = pre_bn_advantages.mean()
bn_advantages_std = pre_bn_advantages.std()
advantages = (pre_bn_advantages - bn_advantages_mean) / (bn_advantages_std + 1e-4)6.3 Verl 框架实现
python
# GDPO 在 Verl 框架中的实现
# 分别处理正确性和格式奖励
correctness_normalized_score, _ = core_algos.compute_grpo_outcome_advantage(
token_level_rewards=token_level_scores_correctness,
...
)
format_normalized_score, _ = core_algos.compute_grpo_outcome_advantage(
token_level_rewards=token_level_scores_format,
...
)
# 相加后再进行掩码白化处理
new_advantage = correctness_normalized_score + format_normalized_score
advantages = masked_whiten(new_advantage, response_mask) * response_mask6.4 代码改动量分析
从上面的代码可以看出,GDPO 相对于 GRPO 的改动非常小:
- 把单次归一化改为循环对每个奖励归一化
- 增加一步批次级归一化
- 总代码改动量约 20 行
这使得 GDPO 可以作为 GRPO 的即插即用替代品。
7. 深度思考与启示
7.1 为什么归一化顺序如此重要?
这个问题的本质是信息保留。
当我们先求和再归一化时,不同奖励组合之间的差异被"压缩"了。这就像把不同颜色的颜料混合后再调色------你已经无法恢复原来的颜色了。
而先分别归一化再求和,相当于先把每种颜色调到相同的亮度,再混合。这样每种颜色的贡献是均衡的,最终的混合色能更好地反映各种颜色的特点。
7.2 批次级归一化的必要性
为什么需要第三步的批次级归一化?
这是因为当奖励数量增加时,求和后的优势值范围也会增加。如果不进行归一化,可能会导致:
- 梯度过大,训练不稳定
- 不同批次之间的优势值范围差异过大
批次级归一化确保了优势值始终在一个合理的范围内,保证了训练的稳定性。
7.3 条件奖励的设计哲学
条件奖励的设计体现了一个重要的思想:优先级约束。
在多目标优化中,不同目标的重要性可能不同。简单的加权求和无法很好地处理这种情况,因为:
- 权重需要精心调整
- 难度差异可能需要极大的权重才能抵消
条件奖励提供了一种更优雅的解决方案:通过依赖关系来强制优先级。这类似于约束优化中的"主约束"和"次约束"的概念。
7.4 对未来研究的启示
-
多奖励 RL 的设计原则:在设计多奖励系统时,需要仔细考虑奖励之间的相互作用,避免信息丢失。
-
归一化策略的重要性:归一化不仅仅是一个技术细节,它可能对最终性能有重大影响。
-
简单方法的力量:GDPO 的改动非常简单,但效果显著。这提醒我们,有时候最有效的改进来自于对问题本质的深入理解。
-
条件奖励的潜力:条件奖励为处理多目标优先级提供了一种新思路,值得在更多场景中探索。
7.5 复现建议
如果你想在自己的项目中使用 GDPO,以下是一些建议:
- 从 GRPO 基线开始:先确保你的 GRPO 实现是正确的
- 逐步添加 GDPO 的改动 :
- 首先添加单奖励归一化
- 然后添加批次级归一化
- 最后考虑条件奖励
- 监控训练指标:特别关注不同奖励的收敛情况,确保没有某个奖励主导优化
- 调整超参数:虽然 GDPO 对超参数更鲁棒,但仍需要根据具体任务进行调整
8. 总结与展望
8.1 核心贡献
GDPO 的核心贡献可以总结为:
- 发现问题:揭示了 GRPO 在多奖励场景下的"优势崩溃"问题
- 提出方案:通过解耦归一化策略解决了这个问题
- 验证有效性:在三大任务上全面超越 GRPO
- 开源实现:提供了 TRL、Verl、Nemo-RL 三个框架的实现
8.2 主要优势
- 简单有效:代码改动量小,效果提升显著
- 通用性强:适用于各种多奖励场景
- 稳定性好:避免了训练过程中的优势崩溃问题
- 即插即用:可以直接替换现有的 GRPO 实现
8.3 局限性
- 当奖励数量非常多时,计算开销会增加
- 条件奖励的阈值需要根据具体任务调整
- 对于某些特殊的奖励结构,可能需要进一步优化
8.4 未来方向
- 自适应权重:自动学习不同奖励的权重
- 层次化奖励:支持更复杂的奖励依赖结构
- 理论分析:从理论上分析 GDPO 的收敛性质
- 更多应用:在更多任务上验证 GDPO 的效果
📚 参考资料
- 论文链接 :arXiv:2601.05242
- 项目主页 :https://nvlabs.github.io/GDPO/
- GitHub 代码 :