6.吴恩达机器学习——TensorFlow与激活函数

TensorFlow训练细节

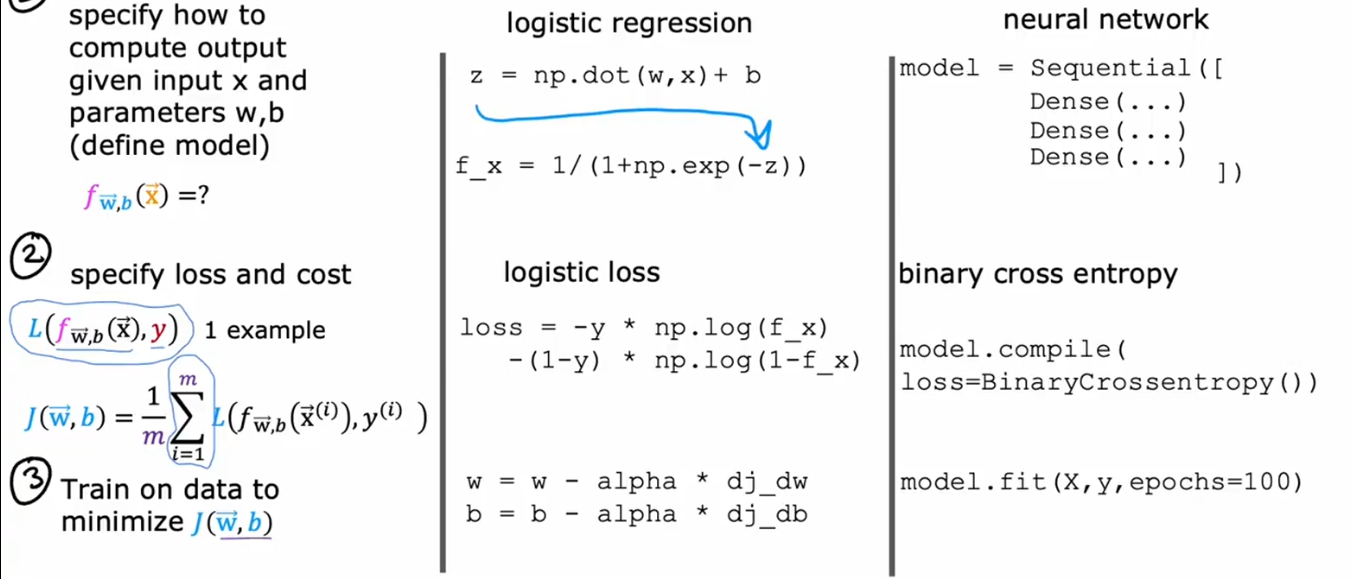
对比逻辑回归步骤，在TensorFlow中训练一个神经网络也有三步：网络层定义，损失函数定义，模型拟合；现在的深度学习大部分都是进行的调库使用，理解库中的实现细节有助于我们产生不同想法，要知其然，还要知其所以然。

1.网络层定义

通过Dense（）来定义密集层结构，对应于逻辑回归中的第一步

2.损失函数定义

在逻辑回归中，我们通过计算损失函数以及对应的成本函数来实现，而在model.compile(loss=...)中，可以直接使用model.compile(loss=...)来实现

3.数据拟合归一化

在逻辑回归中，计算了成本函数之后，要通过迭代更新，不断更新w和b的值，从而降低成本函数的值，在TensorFlow中使用model.fit()即可实现

激活函数的选择和重要性

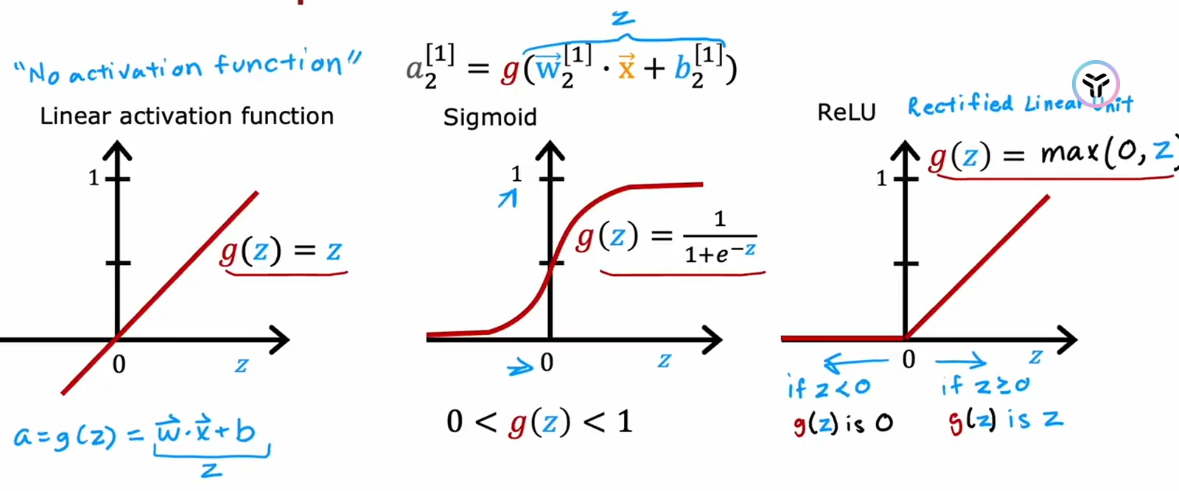
1.输出层激活函数选择

在为输出层选择激活函数时候，你通常根据你要预测的Y，会有一个相当自然的选择

如果你正在实现二分类任务，使用sigmoid是最好的选择
如果你正在实现回归任务,Y可正可负，使用linear线性激活函数
如果回归问题中，最终结果非负，使用ReLU激活函数

2.隐藏层激活函数选择

ReLU激活函数是最佳的选择，相比与sigmoid激活函数，ReLU计算速度更快，且只有在图像的左侧才会有平坦的值，这样在计算成本函数时候得到的成本函数的图像会有更好的梯度下降趋势

下图展示的是使用sigmoid造成的成本函数有多个平坦的地方，这就导致梯度下降缓慢

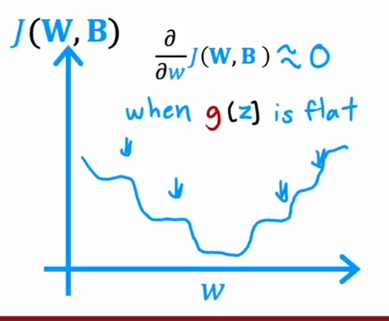
综合选择：隐藏层使用ReLU激活函数，输出层使用sigmoid激活函数

除此之外还有其他更多的激活函数，读者可以自行网上搜索学习

多分类问题激活函数选择

1.什么是多分类

多分类问题本质上是二分类问题的扩展，输出的Y不仅仅是0或者1，可能还有其他更多的值

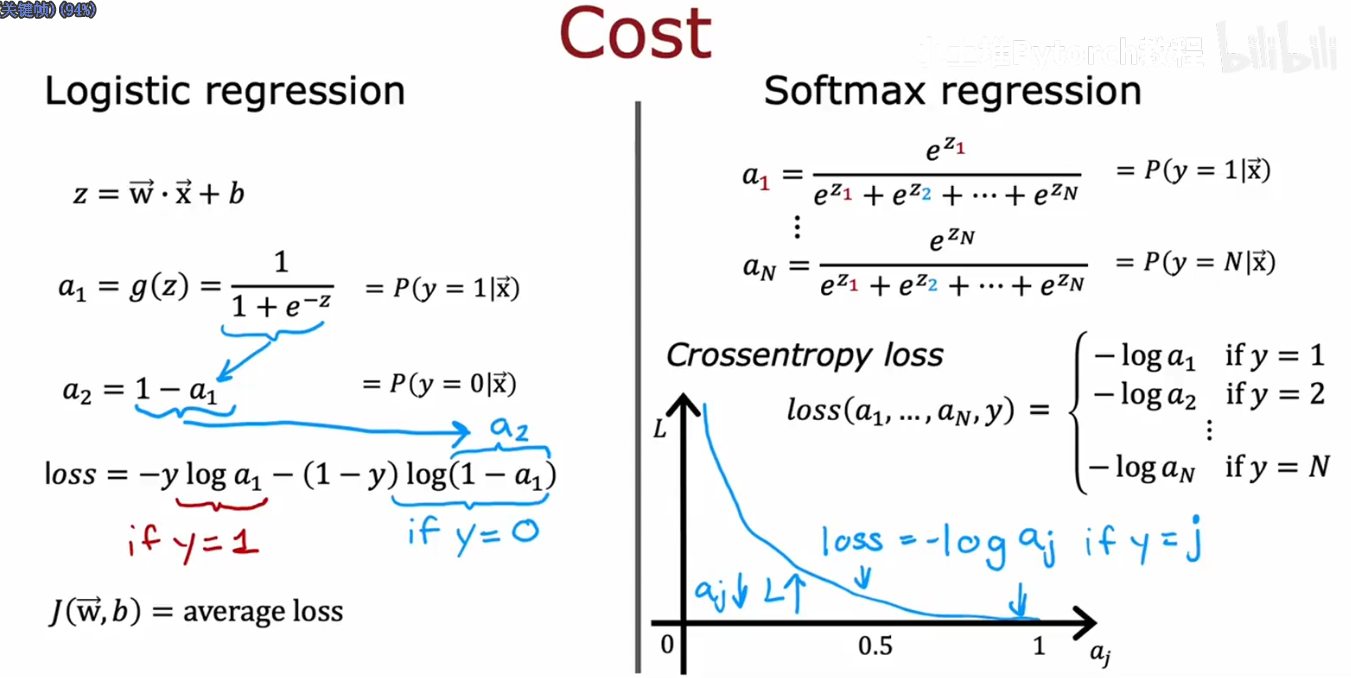
2.Softmax回归算法

Softmax回归是逻辑回归的泛化，适用于多分类任务

公式实现

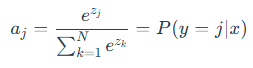
且a1+a2+a3+...+an=1;下图详细展示了softmax函数的使用

损失函数实现

以下是逻辑回归和softmax回归损失函数的定义

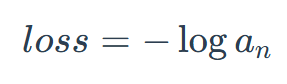
3.softmax的神经网络实现

但在实际应用中一般不使用这段代码，因为在使用过程中可能会产生数值舍入误差，

复制代码

import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
model = Sequential([
    Dense(units=25, activation='relu'),
    Dense(units=15, activation='relu'),
    Dense(units=10, activation='linear')])
from tensorflow.keras.losses import
SparseCategoricalCrossentropy
model.compile(...,loss=SparseCategoricalCrossentropy(from_logits=True))
# (from_logits=True) 是关键
model.fit(X,Y,epochs=100)
predict	logits = model(X)
f_x = tf.nn.softmax(logits)


model = Sequential([
    Dense(units=25, activation='sigmoid'),
    Dense(units=15, activation='sigmoid'),
    Dense(units=1, activation='linear')
])
from tensorflow.keras.losses import BinaryCrossentropy
model.compile(..., BinaryCrossentropy(from_logits=True))
model.fit(X,Y,epochs=100)
logit = model(X)
f_x = tf.nn.sigmoid(logit)

由于我们将最后的输出层都转为了linear作为激活函数，在最后为了得到使用sigmoid或者softmax函数实现的预测，我们就需要在最后对数据使用tf.nn.softmax(logits)或者tf.nn.sigmoid(logit)来实现逻辑函数的映射，从而得到正确的概率值

梯度下降优化Adam优化器

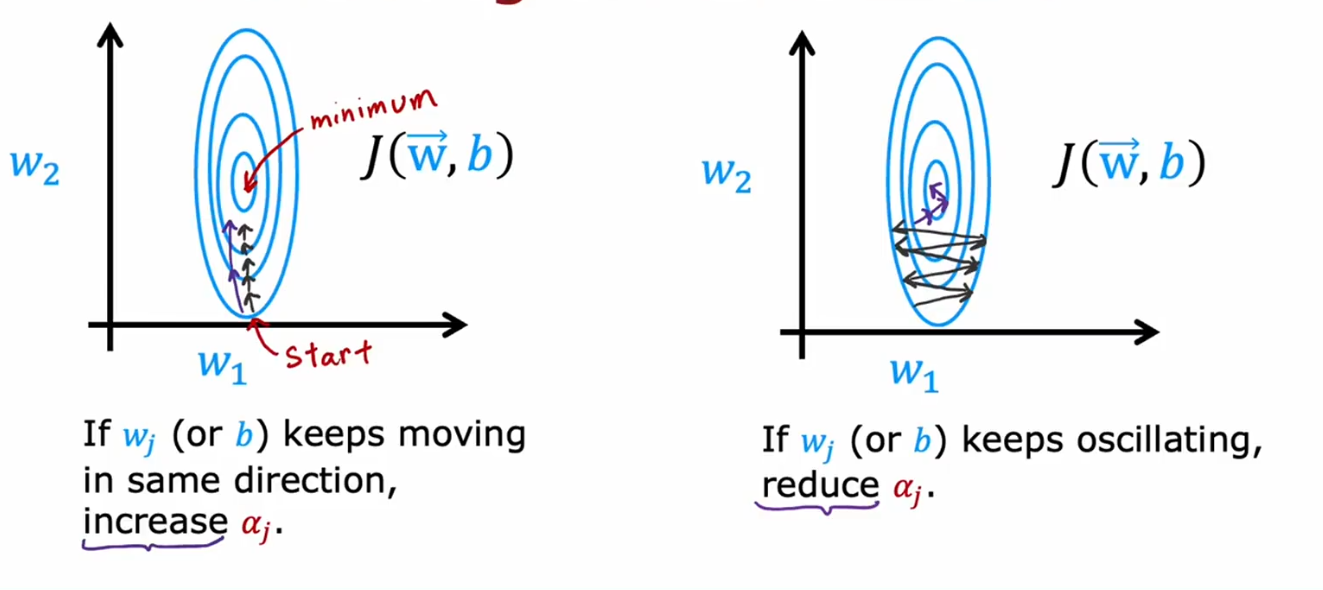
1.作用

动态的调整学习率的大小

当我们梯度下降方向基本不变时候我们需要较大的学习率，以减少迭代次数
当我们梯度下降方向会来回抖动啥时候，我们就需要较小的学习率，来使得下降方向变得平缓

Adam不会使用固定的学习率，而是为每个参数使用不同的学习率

2.代码实现

卷积层(convolutional layer)

前面课程中，我们一直学习的是全连接层，每一层隐藏层的神经元都由上一层的全部神经元计算得来，而卷积层中的每一个神经元只看前一层的部分内容，这会提高计算效率，降低过拟合风险

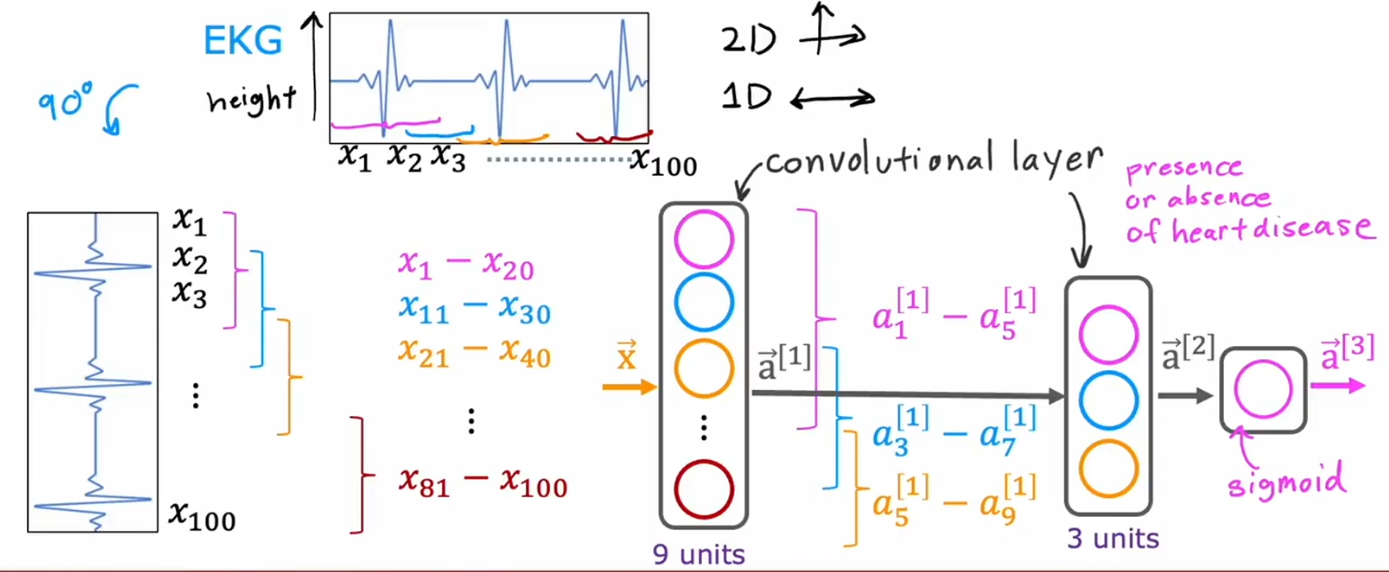
以上例子是吴恩达老师所举心电图例子，卷积层中单个神经元只看部分数据