强化学习导论与多臂老虎机（MAB）核心内容。
导论部分梳理了价值学习、策略学习及 actor-critic 三种架构，阐述深度强化学习的参数化 优势与前沿研究方向；
MAB 部分聚焦探索与利用 平衡问题，通过伯努利老虎机仿真 ，详细介绍 ε-greedy（含衰减型）、
积极初始化 、上置信界 （UCB）及汤普森采样四种经典算法的原理、实现与实验验证，为强化学习入门奠定基础。
目录
[1. Introduction](#1. Introduction)
[2. 探索与利用 -- MAB 为例](#2. 探索与利用 -- MAB 为例)
[2.1 问题建模](#2.1 问题建模)
[2.2 代码仿真](#2.2 代码仿真)
[2.3 方法](#2.3 方法)
[1. 添加策略噪声 ε-greedy](#1. 添加策略噪声 ε-greedy)
[2. 积极初始化 (Optimistic Initialization)](#2. 积极初始化 (Optimistic Initialization))
[3. 上置信界（upper confidence bound，UCB）](#3. 上置信界（upper confidence bound，UCB）)
[4. 汤普森采样算法 Thompson sampling](#4. 汤普森采样算法 Thompson sampling)
1. Introduction
将期望奖励的第一个量提取出来，后面的项为 Q(s',a') 得到 Bellman 方程。
1.1 关于 actor 策略学习 or critic 价值学习的三种架构：
1. 价值学习 只用 critic：我得到精准的 Q(s,a) 然后我每次选 argmax a。
局限性：**Q不准？**得到的 a 可能反而很差；存在偏差。
2. 策略学习 只用 actor：直接优化 J(π)，policy 本身。
3. actor-critic：critic 告诉在 actor 本身的基础上 怎么做更好。不止是 actor 自己和环境交互。
不会游泳的游泳教练；或者像人机交互，人类可能自己不完全清楚怎么写，但可以指导 LLM 一步一步写。
1.2 深度强化学习与参数化
下面这种表格 在状态动作很多的情况下，需要用神经网络近似 -> 深度强化学习：
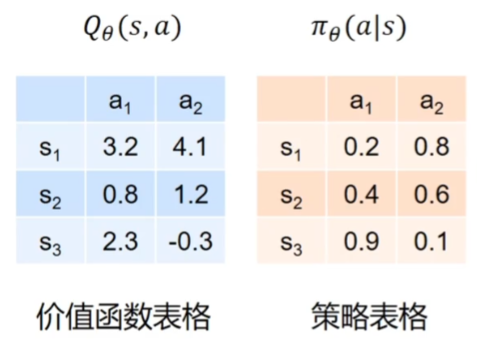
Playing Atari with Deep Reinforcement Learning 第一篇 DRL 论文
参数化的好处：不受数据集或者 |S| |A| 大小的复杂度影响。确定需要多少显存等等。
并且深度学习端到端 可以不用以前研究 Atari 游戏 一帧一帧抽取特征。更容易在实际问题 work。
data resembling + regulization 等方法，使得学习过程数据变化稳定，policy 不在局部过拟合。
CPU（收集经验数据）和GPU（训练神经网络）之间的平衡；两方算力平衡。
1.3 前沿研究方向：
-
需要收集大量数据 ，不从物理世界来的话 需要 buildsimulator；to real transfer 从模拟到现实。
-
很长的任务（几十万帧）需要任务分解分层 + 上下层模块传递结合；
-
imitation learning 模仿学习 （没有reward）先学习人类范例 得到一个好的初始化。
-
分散式 去中心化的个体；不太好用一个中心 system 统一控制 -> 多智能体强化学习 Multi-agent RL
好的性质，去掉 or 增加 几个智能体整体变化不大，对数量不敏感。
-
data privacy 或者算力限制 -> 离线强化学习 ；先在一个确定数据集初始训练，再上线测试
-
大模型agent：目前能做到自己调用工具 + 规划，但没有持续自我优化的过程。
2. 探索与利用 -- MAB 为例
去一家以前去过 的很好吃的餐馆 or 探索（收集数据）一家没吃过的餐馆
美团 or 淘宝推荐系统：用户买什么 就推什么(不最优 但调整算法反而结果更差)只利用不探索不行
新闻 / 社交软件推送：帮助用户不陷在信息茧房中
2.1 问题建模
多臂老虎机（multi-armed bandit，MAB）：
K个杆子，每个杆子的奖励概率固定但是未知 ；在指定拉动次数下 最大化奖励。
与环境交互学习 但是没有实质的状态 ；不会被 state transition 带来的噪音左右。
每个 arm 可以一边玩，一边增量式 O(1) 更新平均值。
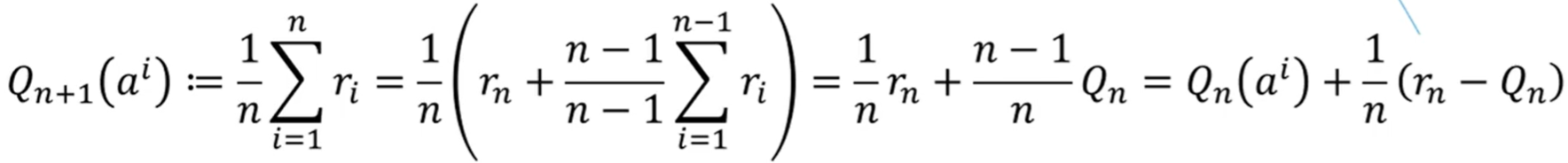
伪代码流程为：
这个问题的 **Q(a)**就是每个杆子弹出奖励的概率（做这个工作的期望回报）
定义 regret 后悔值为 当前决策与最优决策Q* （那个实际上奖励概率最大的杆子）的差异。
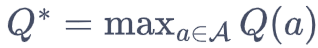
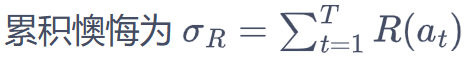因为 Q* 是确定的，max {Q(a)} 等价于 min{σ}
纯探索（比如 p的概率探索新的）：那这个探索 一定会出现选的不是最优的情况，误差无法收敛。
纯利用：根据前面的探索，确定了一个杆子（后来只拉它），这个杆子有概率不是实际最优的 R>0；那么随着 T 趋于无穷，总误差值也跟着趋于无穷。
前期信息比较少，对哪个杆子好的把握比较低，需要探索去收集更多的信息 区分杆子。
2.2 代码仿真
一个 MAB 类模拟，每个杆子的概率 ；step 为选中一个杆子，随机数 是否得到奖励。
python
import numpy as np
class BernoulliBandit:
""" 伯努利多臂老虎机,输入K表示拉杆个数 """
def __init__(self, K):
self.K = K
self.probs = np.random.uniform(size=K) # 随机生成K个0～1的数,作为拉动每根拉杆的获奖
self.best_idx = np.argmax(self.probs) # 获奖概率最大的拉杆
self.best_prob = self.probs[self.best_idx] # 最大的获奖概率
def step(self, k):
# 当玩家选择了k号拉杆后,根据拉动该老虎机的k号拉杆获得奖励的概率返回1（获奖）或0（未获奖）
if np.random.rand() < self.probs[k]:
return 1
else:
return 0
np.random.seed(42) # 设定随机种子,使实验具有可重复性
K = 10
bandit_10_arm = BernoulliBandit(K)求解器类：记录每轮的行动和累积后悔值；每个杆子被拉次数。
run(步数)；每个循环 run_one_step（选中第 k 个杆子，不同方法仅这里不同） 一下。
python
class Solver:
""" 多臂老虎机算法基本框架 """
def __init__(self, bandit):
self.bandit = bandit
self.counts = np.zeros(self.bandit.K) # 每根拉杆的尝试次数
self.regret = 0. # 当前步的累积懊悔
self.actions = [] # 维护一个列表,记录每一步的动作
def run_one_step(self):
# TODO 选哪个
raise NotImplementedError
def run(self, num_steps):
# 运行一定次数,num_steps为总运行次数
for _ in range(num_steps):
k = self.run_one_step()
self.counts[k] += 1
self.actions.append(k)
self.regret += self.bandit.best_prob - self.bandit.probs[k]
self.regrets.append(self.regret)画图 横坐标为时间步，纵坐标为后悔值。
python
import matplotlib.pyplot as plt
def plot_results(solvers, solver_names):
"""生成累积懊悔随时间变化的图像。输入solvers是一个列表,列表中的每个元素是一种特定的策略。
而solver_names也是一个列表,存储每个策略的名称"""
for idx, solver in enumerate(solvers):
time_list = range(len(solver.regrets))
plt.plot(time_list, solver.regrets, label=solver_names[idx])
plt.xlabel('Time steps')
plt.ylabel('Cumulative regrets')
plt.title('%d-armed bandit' % solvers[0].bandit.K)
plt.legend()
plt.show()2.3 方法
1. 添加策略噪声 ε-greedy
estimates 为更新的平均值；每次 < epsilon 就随机；否则选 argmax
python
class EpsilonGreedy(Solver):
""" epsilon贪婪算法,继承Solver类 """
def __init__(self, bandit, epsilon=0.01, init_prob=1.0):
super(EpsilonGreedy, self).__init__(bandit)
self.epsilon = epsilon
#初始化拉动所有拉杆的期望奖励估值
self.estimates = np.array([init_prob] * self.bandit.K)
def run_one_step(self):
if np.random.random() < self.epsilon:
k = np.random.randint(0, self.bandit.K) # 随机选择一根拉杆
else:
k = np.argmax(self.estimates) # 选择期望奖励估值最大的拉杆
r = self.bandit.step(k) # 得到本次动作的奖励
self.estimates[k] += 1. / (self.counts[k] + 1) * (r - self.estimates[k])
return k不同 epsilon 的表现。建立 solver_list 然后都跑 5000 步。
python
np.random.seed(42)
epsilons = [0, 1e-4, 0.01, 0.1, 0.25, 0.5]
K = 200
epsilon_greedy_solver_list = [
EpsilonGreedy(BernoulliBandit(K), epsilon=e) for e in epsilons
]
epsilon_greedy_solver_names = ["epsilon={}".format(e) for e in epsilons]
for solver in epsilon_greedy_solver_list:
solver.run(5000)
plot_results(epsilon_greedy_solver_list, epsilon_greedy_solver_names)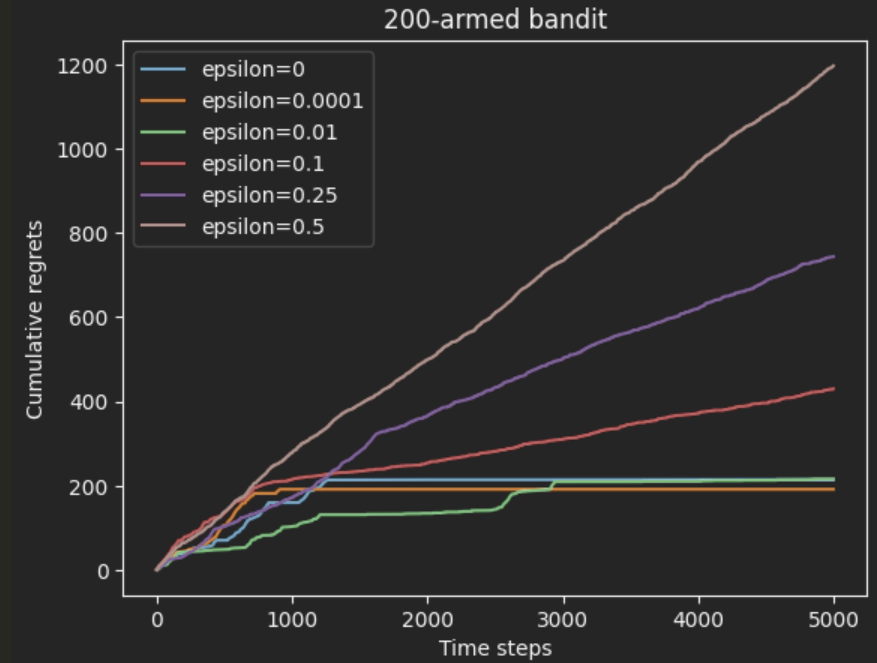
衰减的epsilon ，区别在于 把固定的 epsilon 改成步数的倒数。
python
class DecayingEpsilonGreedy(Solver):
""" epsilon值随时间衰减的epsilon-贪婪算法,继承Solver类 """
def __init__(self, bandit, init_prob=1.0):
super(DecayingEpsilonGreedy, self).__init__(bandit)
self.estimates = np.array([init_prob] * self.bandit.K)
self.total_count = 0
def run_one_step(self):
self.total_count += 1
if np.random.random() < 1 / self.total_count: # epsilon值随时间衰减
k = np.random.randint(0, self.bandit.K)
else:
k = np.argmax(self.estimates)
r = self.bandit.step(k)
self.estimates[k] += 1. / (self.counts[k] + 1) * (r - self.estimates[k])
return k2. 积极初始化 (Optimistic Initialization)
reward 最大是 1，我把所有的 Q(a) 都初始化比较高，更新会让 Q 掉下来。
被更新次数少的，Q还比较大，相当于鼓励多去探索探索次数少的（一种启发式）
坑点：实现的时候 概率初始化需要是浮点数；如果是整数的话 后面的加除运算 保留了整数。
python
np.random.seed(42)
initial = [1.0, 2.0, 3.0, 4.0, 5.0] # 不同的初始期望奖励估值 坑点要设置浮点数而不是整数
K = 200
epsilon_greedy_solver_list = [
EpsilonGreedy(BernoulliBandit(K), epsilon=0.01, init_prob=a) for a in initial
]
epsilon_greedy_solver_names = ["init_prob={}".format(a) for a in initial]
for solver in epsilon_greedy_solver_list:
solver.run(5000)
plot_results(epsilon_greedy_solver_list, epsilon_greedy_solver_names)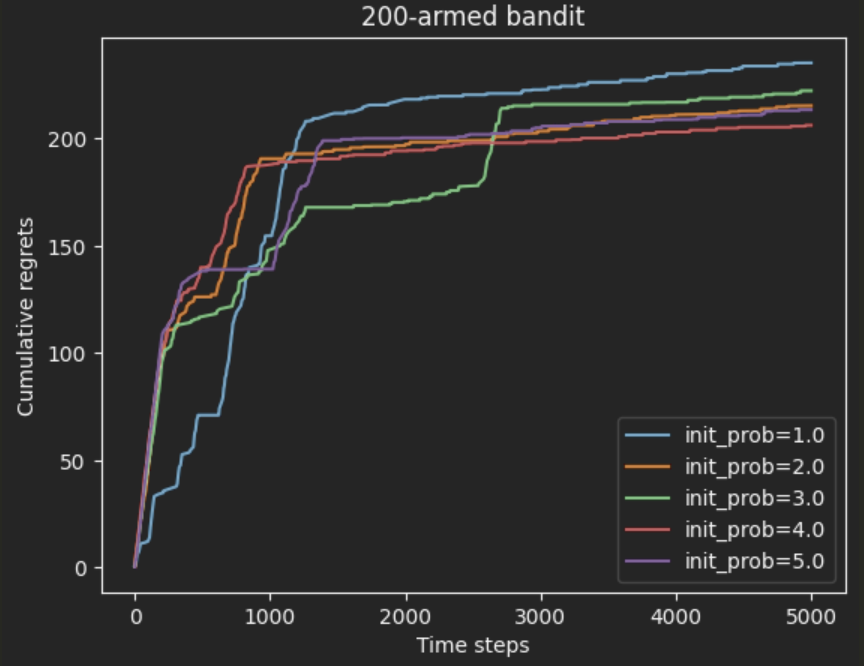
3. 上置信界（upper confidence bound，UCB）
探索次数越少，不确定性越大，方差越大，探索的价值越大。
霍夫丁不等式，期望高于某范围的概率 不超过 ***；令等式右侧为一个 很小的常数阈值概率 p。
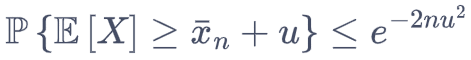则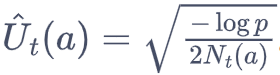 
概率阈值 p 固定时，U 和探索次数 N 负相关。探索次数越少 补偿 U 越多。
从选平均收益最大的动作 -> 加上U选上限（分位数）最大的动作，Q(a) -> Q(a) + U(a)
还可以在 U 前乘以一个权重 coef 作为一个超参数。
实现的时候 可以把 p 设置为 步数的倒数 1/N ；防止分母为 0，进行分母 +1，最终 U 为：
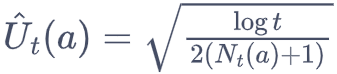
python
class UCB(Solver):
""" UCB算法,继承Solver类 """
def __init__(self, bandit, coef, init_prob=1.0):
super(UCB, self).__init__(bandit)
self.total_count = 0
self.estimates = np.array([init_prob] * self.bandit.K)
self.coef = coef
def run_one_step(self):
self.total_count += 1
ucb = self.estimates + self.coef * np.sqrt(
np.log(self.total_count) / (2 * (self.counts + 1))) # 计算上置信界
k = np.argmax(ucb) # 选出上置信界最大的拉杆
r = self.bandit.step(k)
self.estimates[k] += 1. / (self.counts[k] + 1) * (r - self.estimates[k])
return k4. 汤普森采样算法 Thompson sampling
假设拉动每根拉杆的奖励服从一个特定的概率分布，每次根据分布 为每个杆子采样。
采样结果最高的杆子 被选中，得到 reward，并更新这个杆子的分布。
Beta 分布如下，正比于 α-1 次得到奖励，β-1次未得到奖励。
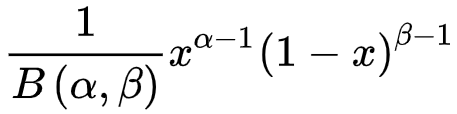每个杆子只需要记录，几次获得奖励，几次无奖励。
python
class ThompsonSampling(Solver):
""" 汤普森采样算法,继承Solver类 """
def __init__(self, bandit):
super(ThompsonSampling, self).__init__(bandit)
self._a = np.ones(self.bandit.K) # 全1列表,表示每根拉杆奖励为1的次数
self._b = np.ones(self.bandit.K) # 全1列表,表示每根拉杆奖励为0的次数
def run_one_step(self):
samples = np.random.beta(self._a, self._b) # 按照Beta分布采样一组奖励样本
k = np.argmax(samples) # 选出采样奖励最大的拉杆
if self.bandit.step(k) == 1:
self._a[k] += 1 # 获得奖励 a++
else:
self._b[k] += 1 # 未获得奖励 b++
return k