首先通过基于Terzaghi和Meyerhof经典理论的模拟数据生成模块,创建了大量符合工程实际的训练样本,这些样本不仅包含基本的土体参数(粘聚力、内摩擦角、重度)和基础几何参数(宽度、长度、埋深),还添加了荷载条件(倾角、偏心距)以及根据工程经验修正的多种衍生特征(上覆压力、长宽比、刚度指标等)。然后,系统构建了一个物理信息约束的深度神经网络模型,该模型在传统神经网络的基础上,通过自动微分技术计算梯度,强制模型满足承载力随关键土体参数单调递增、预测值为正且在合理范围内的物理规律,同时采用混合损失函数(MSE、MAE、Huber)平衡训练稳定性与对异常值的鲁棒性。在训练过程中,系统采用自适应学习率调度和早停策略,防止过拟合,并实时监控物理约束损失与数据损失的平衡。训练完成后,系统进行全面的性能评估,不仅计算常规回归指标(RMSE、MAE、R²),还提供误差分布、相对误差分析、预测准确度分级等工程实用指标,并与传统经典公式进行对比验证。最终,系统提供了完整的模型部署功能,包括预测接口、安全系数建议和工程设计值范围推荐,形成了一个从数据生成、模型训练、性能评估到工程应用的完整闭环系统。

第一步:数据模拟与生成
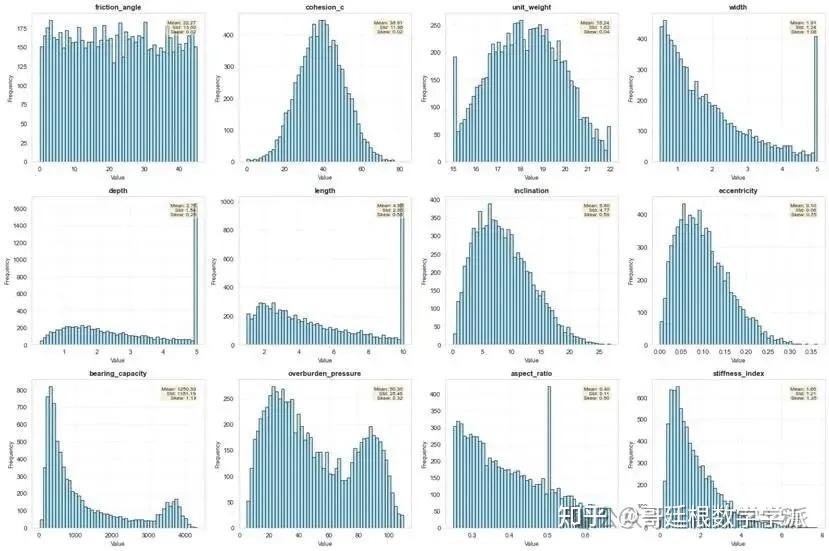
基于经典土力学理论(Terzaghi和Meyerhof公式),模拟生成符合工程实际的训练数据集。首先随机生成具有相关性的土体参数(内摩擦角与粘聚力负相关)、基础几何参数(宽度与埋深相关)、荷载条件(倾角和偏心距)。然后应用经典承载力公式计算理论值,接着根据工程经验添加修正因子(埋深修正、倾角修正、形状修正、偏心修正)和安全系数,最后添加有偏噪声模拟实测误差,并计算多种衍生特征增强模型学习能力。
第二步:数据预处理与划分
将生成的数据集按比例划分为训练集、验证集和测试集。对输入特征使用鲁棒标准化方法进行归一化处理,减少异常值影响。对承载力目标变量进行对数变换,改善其偏态分布,使模型训练更稳定。
第三步:物理信息神经网络构建
设计深度神经网络架构,包含多个全连接层,每层后接批量归一化和ReLU激活函数,使用Dropout防止过拟合。特别地,在模型初始化时考虑物理先验知识,并设计物理约束损失函数,通过自动微分计算承载力对各输入参数的梯度,强制模型满足单调性关系(承载力随粘聚力、内摩擦角、埋深增加而增加),同时确保预测值为正且在合理范围内。
第四步:混合损失函数设计
结合均方误差、平均绝对误差和Huber损失构建混合损失函数,平衡不同误差度量的优势:均方误差强调大误差惩罚,平均绝对误差对异常值更鲁棒,Huber损失结合了两者优点。将数据损失与物理约束损失加权求和作为总损失函数。
第五步:模型训练与优化
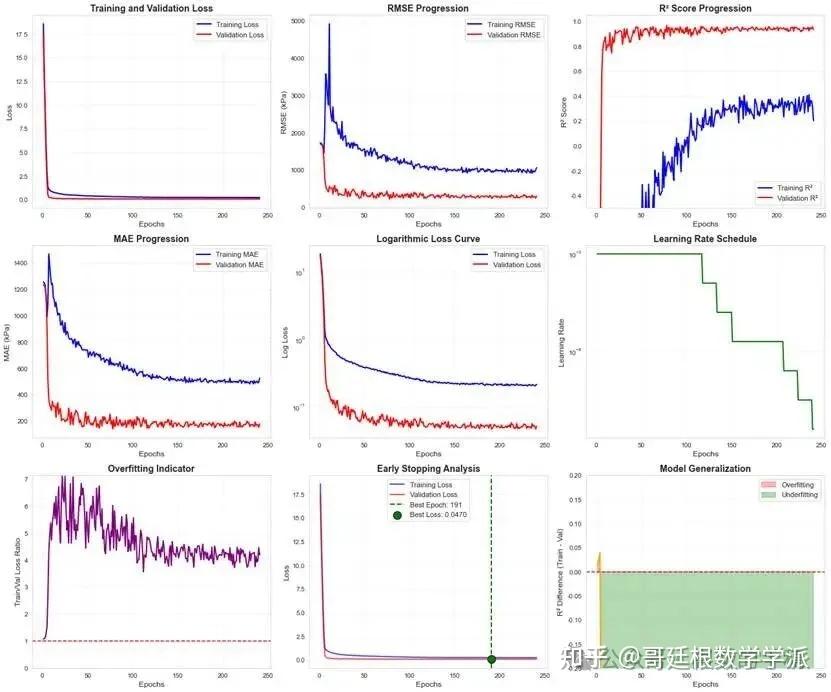
使用AdamW优化器进行参数更新,结合权重衰减提高泛化能力。采用动态学习率调度策略,根据验证集损失自动降低学习率。实施早停机制,当验证集损失连续多轮不再改善时停止训练,保存验证性能最佳模型。训练过程中实施梯度裁剪,防止梯度爆炸。
第六步:综合性能评估
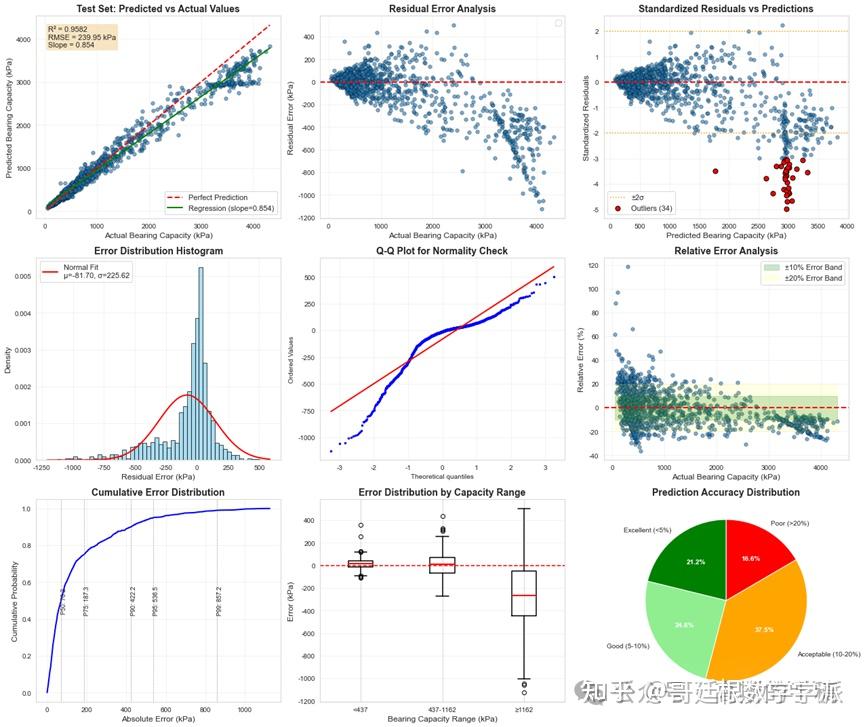
在独立测试集上全面评估模型性能,不仅计算常规回归指标,还分析误差分布特征、计算百分比误差、进行预测准确度分级统计。特别地,将模型预测结果与传统经典公式计算结果进行对比,量化模型相对于经验公式的改进程度。
第七步:结果可视化与分析
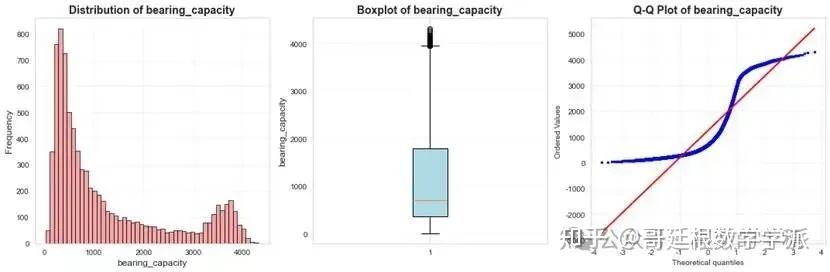
绘制训练过程曲线(损失变化、指标演变、学习率调整),可视化预测值与真实值对比、残差分析、误差分布、分位数图等多种图表,全面诊断模型表现。同时绘制预测准确度分布饼图,直观展示模型在工程应用中的可靠性。
"""
土木工程承载力预测深度学习模型
嵌入领域知识的神经网络实现
"""
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
import matplotlib.pyplot as plt
from matplotlib import rcParams
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, RobustScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
from scipy import stats
import warnings
import pickle
import os
warnings.filterwarnings('ignore')
# 设置中文字体(用于注释)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 设置图表样式
sns.set_style("whitegrid")
rcParams['figure.figsize'] = 10, 6
# ==================== 1. 改进的数据生成模块 ====================
class ImprovedBearingCapacityDataGenerator:
"""
改进的土体承载力数据生成器
基于Terzaghi, Meyerhof等经典承载力理论,添加工程合理性检查
"""
def __init__(self, n_samples=5000, noise_level=0.05, seed=42):
self.n_samples = n_samples
self.noise_level = noise_level
self.seed = seed
np.random.seed(seed)
def generate_parameters(self):
"""生成符合工程实际的输入参数,添加参数相关性"""
# 设置随机种子确保可重复性
np.random.seed(self.seed)
# 基础参数生成
data = {}
# 1. 土体参数(添加参数间的相关性)
# 内摩擦角与粘聚力负相关(通常砂土摩擦角大但粘聚力小,粘土反之)
base_phi = np.random.uniform(0, 45, self.n_samples)
# 粘聚力与内摩擦角负相关
data['friction_angle'] = base_phi
data['cohesion_c'] = 50 - 0.5 * base_phi + np.random.normal(0, 10, self.n_samples)
data['cohesion_c'] = np.clip(data['cohesion_c'], 0, 100)
# 重度:砂土重度大,粘土重度小
data['unit_weight'] = 16 + 0.1 * data['friction_angle'] + np.random.normal(0, 1, self.n_samples)
data['unit_weight'] = np.clip(data['unit_weight'], 15, 22)
# 2. 基础参数(添加工程合理性)
# 基础宽度
data['width'] = np.random.exponential(1.5, self.n_samples) + 0.5
data['width'] = np.clip(data['width'], 0.5, 5)
# 埋深:通常与基础宽度相关
data['depth'] = np.minimum(data['width'] * np.random.uniform(0.5, 3, self.n_samples), 5)
data['depth'] = np.clip(data['depth'], 0, 5)
# 基础长度:通常大于宽度
data['length'] = data['width'] * np.random.uniform(1.5, 4, self.n_samples)
data['length'] = np.clip(data['length'], 1, 10)
# 3. 荷载参数
data['inclination'] = np.random.beta(2, 5, self.n_samples) * 30 # 大多数接近0度
data['eccentricity'] = np.random.beta(2, 8, self.n_samples) * 0.5 # 大多数接近0
return pd.DataFrame(data)
def terzaghi_formula(self, df):
"""Terzaghi承载力公式 - 用于生成基准标签"""
# 提取所需特征,确保存在
required_cols = ['cohesion_c', 'friction_angle', 'unit_weight', 'width', 'depth']
for col in required_cols:
if col not in df.columns:
raise ValueError(f"DataFrame必须包含'{col}'列")
c = df['cohesion_c']
phi = np.radians(df['friction_angle']) # 转换为弧度
gamma = df['unit_weight']
B = df['width']
D = df['depth']
# 处理phi=0的情况
phi_safe = phi.copy()
phi_safe[phi == 0] = 1e-6 # 避免除以0
# 承载力系数(Terzaghi公式)
Nq = np.exp(np.pi * np.tan(phi_safe)) * (np.tan(np.pi/4 + phi_safe/2))**2
Nc = (Nq - 1) / np.tan(phi_safe)
Nc[phi == 0] = 5.7 # 纯粘土的情况
Ngamma = 2 * (Nq + 1) * np.tan(phi_safe)
# Terzaghi承载力公式
q_ult = c * Nc + gamma * D * Nq + 0.5 * gamma * B * Ngamma
return q_ult
def meyerhof_formula(self, df):
"""Meyerhof承载力公式 - 作为对比"""
# 提取所需特征,确保存在
required_cols = ['cohesion_c', 'friction_angle', 'unit_weight', 'width', 'depth', 'length']
for col in required_cols:
if col not in df.columns:
raise ValueError(f"DataFrame必须包含'{col}'列")
c = df['cohesion_c']
phi = np.radians(df['friction_angle'])
gamma = df['unit_weight']
B = df['width']
D = df['depth']
L = df['length']
# Meyerhof承载力系数
Nq = np.exp(np.pi * np.tan(phi)) * (np.tan(np.pi/4 + phi/2))**2
Nc = (Nq - 1) * (1 / np.tan(phi))
Nc[phi == 0] = 5.14
Ngamma = (Nq - 1) * np.tan(1.4 * phi)
# 形状系数
sq = 1 + 0.1 * (B/L) * np.tan(np.pi/4 + phi/2)
sc = 1 + 0.2 * (B/L)
sgamma = 1 + 0.1 * (B/L) * np.tan(phi)
# 深度系数
dq = 1 + 0.1 * (D/B) * np.tan(np.pi/4 + phi/2)
dc = 1 + 0.2 * (D/B)
dgamma = 1
q_ult = c * Nc * sc * dc + gamma * D * Nq * sq * dq + 0.5 * gamma * B * Ngamma * sgamma * dgamma
return q_ult参考文章:
基于物理约束与多源知识融合的浅基础极限承载力智能预测与工程决策优化(以模拟信号为例,Pytorch) - 哥廷根数学学派的文章
https://zhuanlan.zhihu.com/p/1993601797730894324