大模型应用：量化校准：全局/分组 Min-Max、GPTQ、AWQ 算法最优匹配.54

minhuan2026-01-14 8:12

一、引言

一直以来，我们都围绕大模型的本地部署由浅入深的仔细讨论，大模型的落地困境从来离不开"显存"与"速度"，以 LLaMA-7B 为例，FP32 精度下显存占用高达 28GB，普通消费级显卡根本无法承载。而量化，正是把庞然大物塞进普通硬件的核心技术，通过前几期文章我们详细的讲解了采用量化将 32 位浮点数（FP32）转换为 4 位整数（INT4）的过程，可以使显存占用可降低 75%，推理速度提升 4 倍以上。

但在明确量化的核心价值后，我们不得不面对其与生俱来的核心痛点：精度损失。量化本质是对权重数值的"范围压缩"与"离散化映射"，就像用有限的颜料还原复杂画作，若直接按固定规则映射，极易出现细节丢失、极端值干扰等问题。以 INT4 量化为例，仅能使用 0~15 共 16 个离散值承载原始 FP32 的海量信息，若缺乏合理校准，极端值会"绑架"全局量化范围，导致主体权重被过度压缩，模型效果断崖式下降。

正是为解决这一问题而生的精度调节机制，量化校准起到至关重要的作用，它通过优化映射规则，让低精度权重尽可能贴合原始值，平衡"压缩效率"与"精度保留"，是让量化从理论变为实际的关键一步，更是 INT4 等低比特量化落地的核心前提。今天我们也通过通俗易懂的示例，一步步拆解全局 Min-Max、分组 Min-Max、GPTQ、AWQ 四种核心校准算法，剖析其进化逻辑，解释为何分组校准是 INT4 量化的基石，以及 GPTQ/AWQ 如何实现精度与效率的突破，并通过多维度对比，明确不同场景下的最优选择。

二、量化校准基础

1. 核心概念

1.1 量化

量化是将模型的权重从高精度浮点数（如FP32，32位）转换为低精度整数（如INT4，仅4位）的过程。这本质上是信息压缩，将连续的数值范围映射到有限的离散值上。就像将高清照片转为像素画，保留了主要轮廓但减少了细节。

**关键点：**权衡存储与计算效率与精度损失，实现模型瘦身，本质是范围压缩。

1.2 校准

校准是寻找最优映射规则，决定如何将浮点数映射到整数的关键步骤。它需要分析权重的实际分布范围，确定：

  • 缩放因子（scale）：将浮点范围映射到整数范围的比例
  • 零点（zero point）：处理不对称分布时的偏移量

好的校准策略能让量化后的整数尽可能准确还原原始数值，最小化精度损失。常用方法包括基于数据集的统计分析和极值范围校准。

1.3 权重利用率

权重利用率避免数值浪费，INT4仅有16个取值（0~15或-8~7），权重利用率衡量了这些离散值被实际使用的比例：

  • 高利用率（如用到了12个以上值）：表示量化映射较均匀，细节保留较好
  • 低利用率（如仅用到5-6个值）：表明量化区间设置不合理，大量数值空置，精度损失大

**优化目标：**通过调整量化参数，让权重的实际分布尽可能填满可用整数范围，最大化信息保留。

2. 基础公式

2.1 量化公式

将 FP32 权重映射到 INT4（0~15），分三步：归一化→缩放→四舍五入，公式如下：

Q = round [(W - Min) / (Max - Min) × Q_max ]

说明：

    1. W：原始 FP32 权重；
    1. Min/Max：校准确定的最小值/最大值（全局或分组）；
    1. Q_max：INT4 最大值（15，因 2^4 - 1 = 15）；
    1. round：四舍五入，确保结果为整数（INT4 取值）。

2.2 反量化公式

推理时需将 INT4 还原为 FP32 用于计算，公式为量化的逆操作：

W_rec = (Q / Q_max) × (Max - Min) + Min

说明：

    1. W_rec 为反量化后的 FP32 权重
    1. 误差 = |W - W_rec|，误差越小，校准效果越好。

2.3 权重设定

为简化计算并增强理解，我们用一组含极端值的极简权重，贴近真实模型权重分布：大部分为主体权重，少数为极端值：

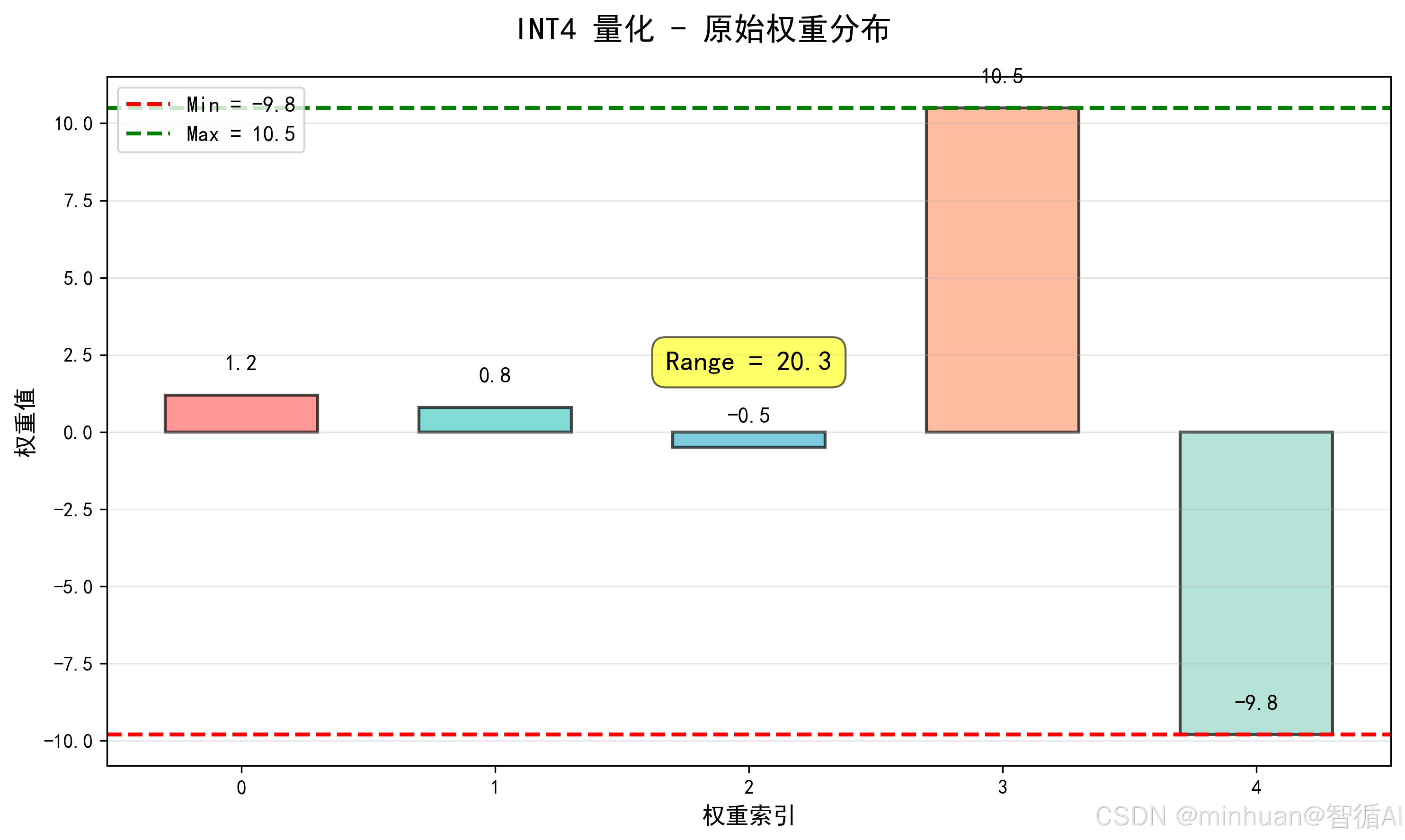
原始权重 W = [1.2, 0.8, -0.5, 10.5, -9.8]

  • 主体权重：1.2、0.8、-0.5，分布在 -0.5~1.2之间；
  • 极端值：10.5、-9.8，远离主体，易绑架量化范围。

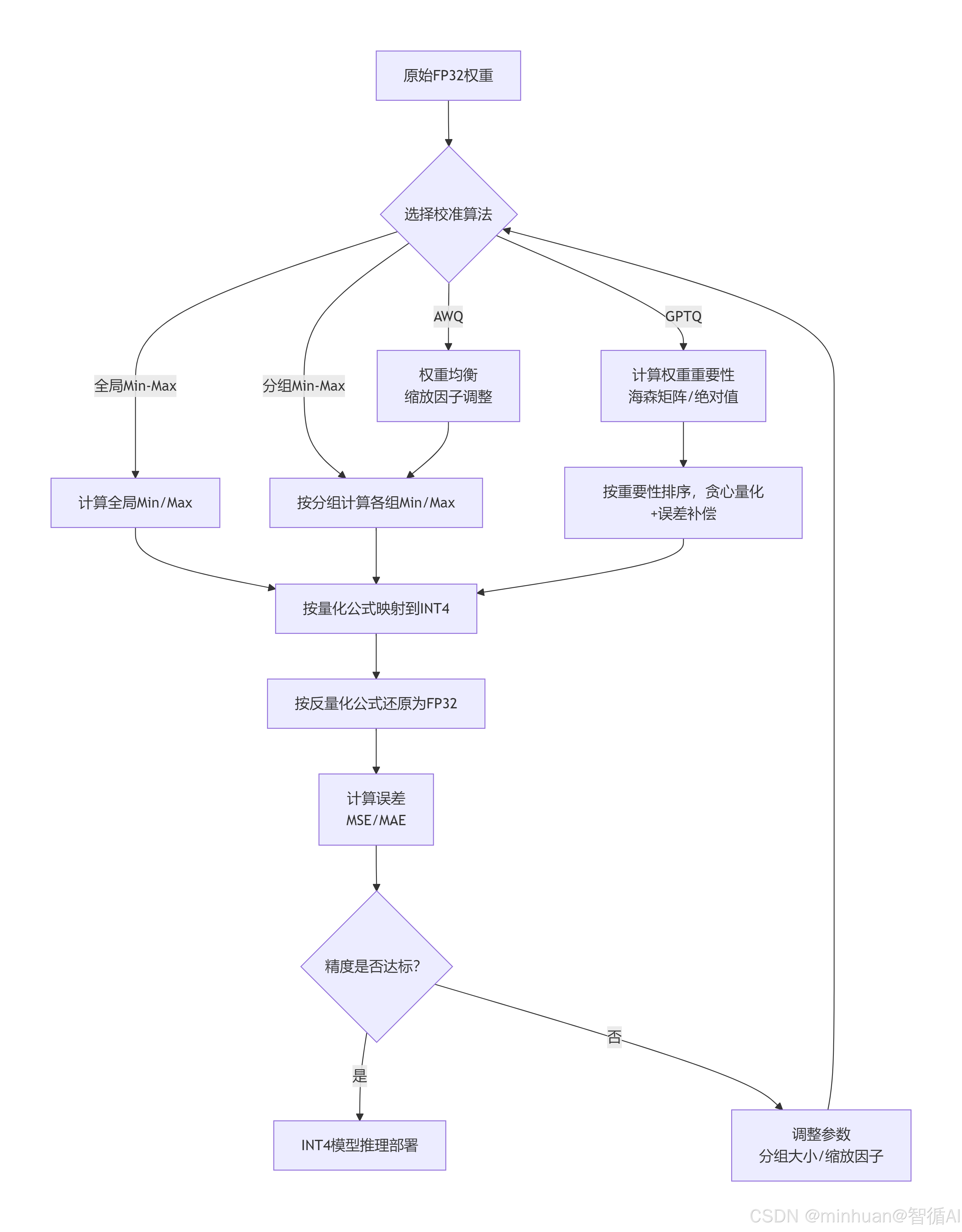
三、校准算法演变

四种算法的演变逻辑是：从忽略权重分布差异，到主动适配分布、优先保障核心权重精度，我们逐一拆解，结合示例计算展示每一步的变化。

1. 初代方案：全局 Min-Max

1.1 核心逻辑

用整个权重数组的 Min/Max作为唯一映射标准，所有权重共用一套规则，就像给羽绒服和袜子定同一个折叠标准，粗暴但简单。

1.2 执行步骤：

就像给所有衣服定一个"统一折叠标准"：

  • 步骤 1：遍历模型所有 FP32 权重，找到最大值（Max）和最小值（Min）；
  • 步骤 2：用公式把每个 FP32 权重映射到 INT4 范围（0~15）：
    • INT4值 = (FP32值 - Min) / (Max - Min) * 15
  • 步骤 3：推理时，再用反向公式还原：FP32值 = (INT4值 / 15) * (Max - Min) + Min

1.3 步骤推理：

    1. 计算全局 Min/Max：Min = -9.8，Max = 10.5，范围 Range = 10.5 - (-9.8) = 20.3；
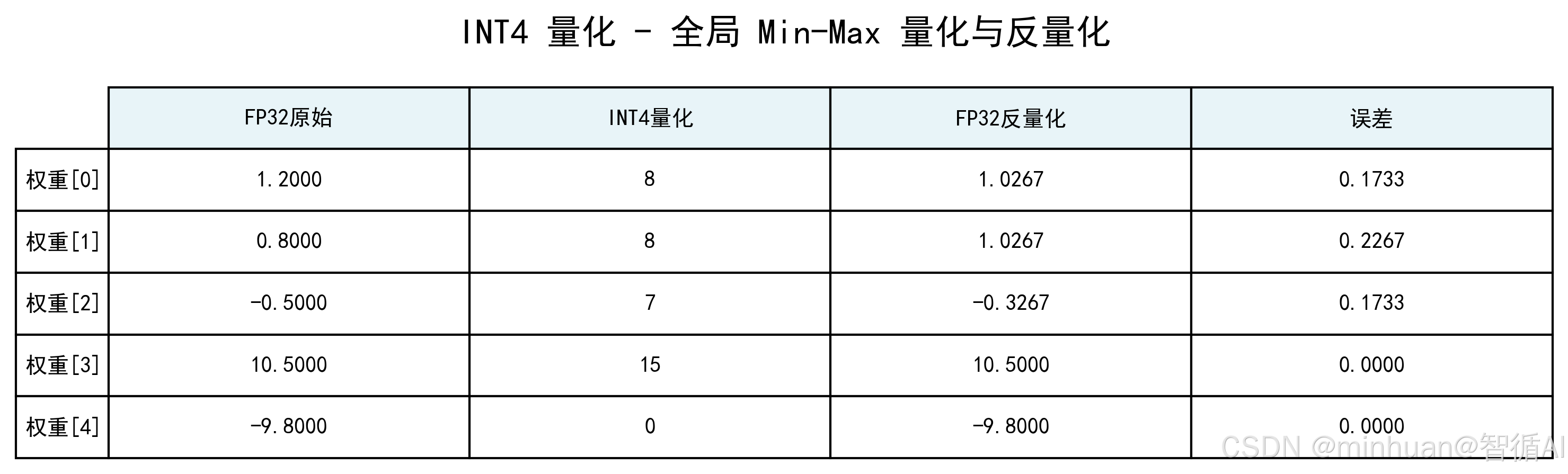
    1. 量化：按公式计算每个权重的 INT4 值，结果为 [8, 8, 7, 15, 0]；
    1. 反量化：还原为 FP32，结果为 [1.0267, 1.0267, -0.3267, 10.5, -9.8]；
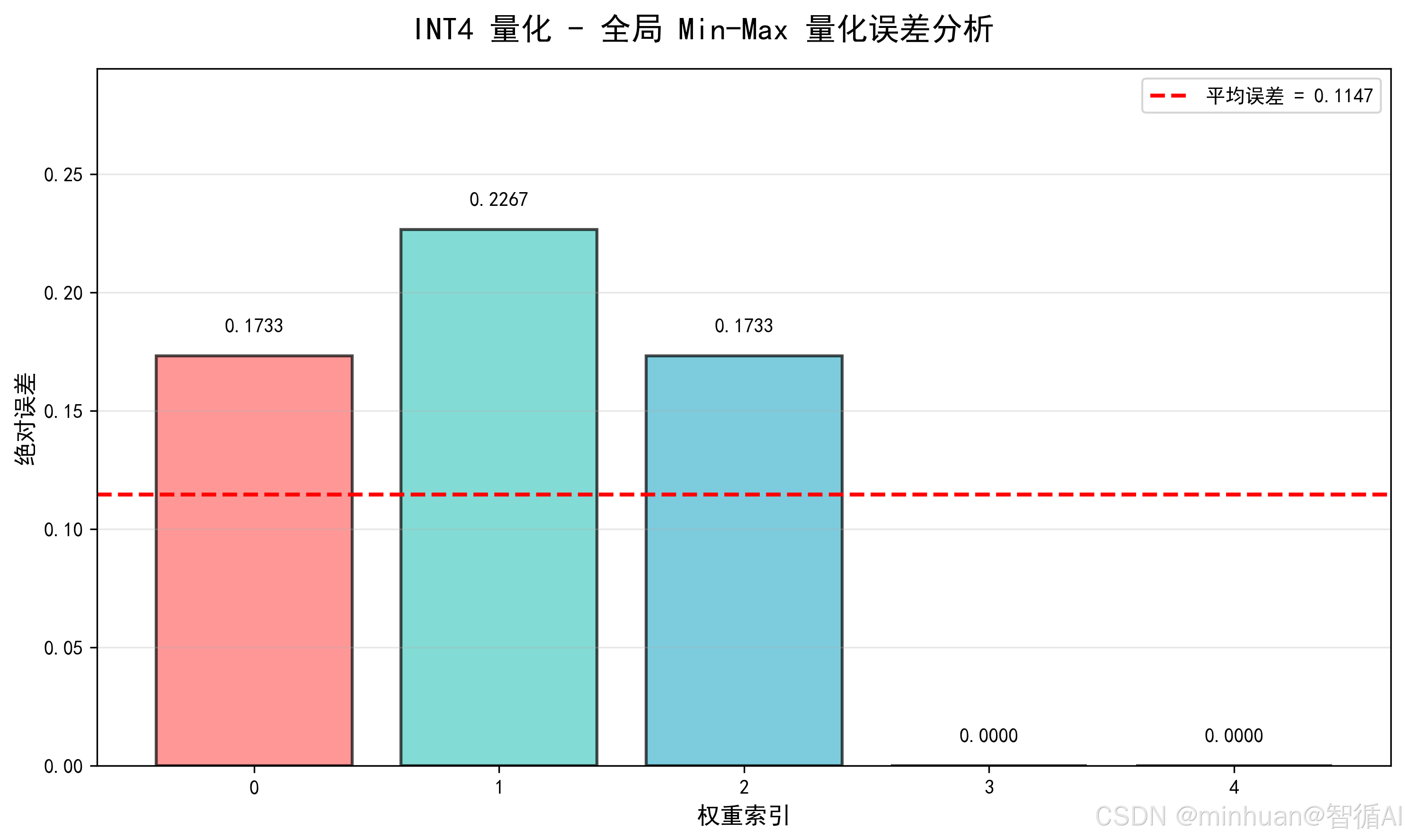
    1. 误差：逐元素误差为 [0.1733, 0.2267, 0.1733, 0, 0]，平均误差 0.1147。

1.4 计算示例：

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import FancyBboxPatch, ConnectionPatch
import matplotlib.gridspec as gridspec

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# ==================== 计算过程 ====================
# 原始权重
weights_fp32 = np.array([1.2, 0.8, -0.5, 10.5, -9.8])

# 1. 计算全局 Min/Max
min_val = -9.8
max_val = 10.5
range_val = max_val - min_val  # 20.3

# 2. 量化到 INT4 (0-15)
# 公式: int4_val = round((x - min) / range * 15)
int4_vals = np.round((weights_fp32 - min_val) / range_val * 15).astype(int)

# 3. 反量化回 FP32
# 公式: fp32_deq = min + int4_val / 15 * range
weights_deq = min_val + int4_vals / 15 * range_val

# 4. 计算误差
errors = np.abs(weights_fp32 - weights_deq)
mean_error = np.mean(errors)

# 打印计算过程
print("=" * 60)
print("全局 Min-Max INT4 量化计算过程")
print("=" * 60)
print(f"1. 计算全局 Min/Max：")
print(f"   Min = {min_val}, Max = {max_val}")
print(f"   Range = {max_val} - ({min_val}) = {range_val}")
print()
print(f"2. 量化到 INT4 (0-15)：")
print(f"   公式: int4_val = round((x - {min_val}) / {range_val} * 15)")
for i, (w, q) in enumerate(zip(weights_fp32, int4_vals)):
    calc = (w - min_val) / range_val * 15
    print(f"   权重[{i}]: {w:.4f} -> ({w:.4f} - {min_val}) / {range_val} * 15 = {calc:.2f} -> {q}")
print(f"   量化结果: {int4_vals.tolist()}")
print()
print(f"3. 反量化回 FP32：")
print(f"   公式: fp32_deq = {min_val} + int4_val / 15 * {range_val}")
for i, (q, d) in enumerate(zip(int4_vals, weights_deq)):
    print(f"   INT4[{i}]: {q} -> {min_val} + {q}/15 * {range_val} = {d:.4f}")
print(f"   反量化结果: {weights_deq.tolist()}")
print()
print(f"4. 计算误差：")
for i, (orig, deq, err) in enumerate(zip(weights_fp32, weights_deq, errors)):
    print(f"   权重[{i}]: |{orig:.4f} - {deq:.4f}| = {err:.4f}")
print(f"   平均误差: {mean_error:.4f}")
print("=" * 60)

# ==================== 可视化 ====================

colors = ['#FF6B6B', '#4ECDC4', '#45B7D1', '#FFA07A', '#98D8C8']

# ===== 图1: 计算全局 Min/Max =====
fig1, ax1 = plt.subplots(figsize=(10, 6))
fig1.suptitle('INT4 量化 - 原始权重分布', fontsize=16, fontweight='bold')

x_pos = np.arange(len(weights_fp32))
bars1 = ax1.bar(x_pos, weights_fp32, width=0.6, color=colors, alpha=0.7, edgecolor='black', linewidth=1.5)
ax1.axhline(y=min_val, color='red', linestyle='--', linewidth=2, label=f'Min = {min_val}')
ax1.axhline(y=max_val, color='green', linestyle='--', linewidth=2, label=f'Max = {max_val}')

for i, w in enumerate(weights_fp32):
    ax1.text(i, w + 0.8, f'{w:.1f}', ha='center', fontsize=11, fontweight='bold')

ax1.set_xlabel('权重索引', fontsize=12)
ax1.set_ylabel('权重值', fontsize=12)
ax1.legend(loc='upper left', fontsize=11)
ax1.grid(True, alpha=0.3, axis='y')
ax1.text(2, 2, f'Range = {range_val}', ha='center', fontsize=14, fontweight='bold',
         bbox=dict(boxstyle="round,pad=0.5", facecolor="yellow", alpha=0.6))

plt.tight_layout()
plt.savefig('260113-原始权重分布.png', dpi=300, bbox_inches='tight')
plt.show()

# ===== 图2: 量化与反量化表格 =====
fig2, ax2 = plt.subplots(figsize=(10, 3))
fig2.suptitle('INT4 量化 - 全局 Min-Max 量化与反量化', fontsize=16, fontweight='bold')

table_data = []
for i in range(len(weights_fp32)):
    table_data.append([
        f'{weights_fp32[i]:.4f}',
        f'{int4_vals[i]}',
        f'{weights_deq[i]:.4f}',
        f'{errors[i]:.4f}'
    ])

ax2.axis('tight')
ax2.axis('off')
table = ax2.table(cellText=table_data,
                  colLabels=['FP32原始', 'INT4量化', 'FP32反量化', '误差'],
                  rowLabels=[f'权重[{i}]' for i in range(len(weights_fp32))],
                  cellLoc='center',
                  loc='center',
                  fontsize=10)
table.auto_set_font_size(False)
table.set_fontsize(10)
table.scale(1.2, 2.5)

# 设置表头样式
for i in range(4):
    table[(0, i)].set_facecolor('#E8F4F8')
    table[(0, i)].get_text().set_weight('bold')

plt.tight_layout()
plt.savefig('260113-全局 Min-Max 量化与反量化.png', dpi=300, bbox_inches='tight')
plt.show()

# ===== 图3: 误差分析 =====
fig3, ax3 = plt.subplots(figsize=(10, 6))
fig3.suptitle('INT4 量化 - 全局 Min-Max 量化误差分析', fontsize=16, fontweight='bold')

bars3 = ax3.bar(range(len(errors)), errors, color=colors, alpha=0.7, edgecolor='black', linewidth=1.5)

for i, (bar, err) in enumerate(zip(bars3, errors)):
    height = bar.get_height()
    ax3.text(bar.get_x() + bar.get_width()/2, height + 0.01,
             f'{err:.4f}', ha='center', fontsize=10, fontweight='bold')

ax3.axhline(y=mean_error, color='red', linestyle='--', linewidth=2,
           label=f'平均误差 = {mean_error:.4f}')
ax3.set_xlabel('权重索引', fontsize=12)
ax3.set_ylabel('绝对误差', fontsize=12)
ax3.legend(fontsize=10)
ax3.set_ylim(0, max(errors) * 1.3)
ax3.grid(True, alpha=0.3, axis='y')

plt.tight_layout()
plt.savefig('260113-全局 Min-Max 量化误差分析.png', dpi=300, bbox_inches='tight')
plt.show()

输出结果：

============================================================

全局 Min-Max INT4 量化计算过程

============================================================
1. 计算全局 Min/Max：

Min = -9.8, Max = 10.5

Range = 10.5 - (-9.8) = 20.3

2. 量化到 INT4 (0-15)：

公式: int4_val = round((x - -9.8) / 20.3 * 15)

权重[0]: 1.2000 -> (1.2000 - -9.8) / 20.3 * 15 = 8.13 -> 8

权重[1]: 0.8000 -> (0.8000 - -9.8) / 20.3 * 15 = 7.83 -> 8

权重[2]: -0.5000 -> (-0.5000 - -9.8) / 20.3 * 15 = 6.87 -> 7

权重[3]: 10.5000 -> (10.5000 - -9.8) / 20.3 * 15 = 15.00 -> 15

权重[4]: -9.8000 -> (-9.8000 - -9.8) / 20.3 * 15 = 0.00 -> 0

量化结果: [8, 8, 7, 15, 0]

3. 反量化回 FP32：

公式: fp32_deq = -9.8 + int4_val / 15 * 20.3

INT4[0]: 8 -> -9.8 + 8/15 * 20.3 = 1.0267

INT4[1]: 8 -> -9.8 + 8/15 * 20.3 = 1.0267

INT4[2]: 7 -> -9.8 + 7/15 * 20.3 = -0.3267

INT4[3]: 15 -> -9.8 + 15/15 * 20.3 = 10.5000

INT4[4]: 0 -> -9.8 + 0/15 * 20.3 = -9.8000

反量化结果: [1.0266666666666655, 1.0266666666666655, -0.3266666666666662, 10.5, -9.8]

4. 计算误差：

权重[0]: |1.2000 - 1.0267| = 0.1733

权重[1]: |0.8000 - 1.0267| = 0.2267

权重[2]: |-0.5000 - -0.3267| = 0.1733

权重[3]: |10.5000 - 10.5000| = 0.0000

权重[4]: |-9.8000 - -9.8000| = 0.0000

平均误差: 0.1147

============================================================

1.5 主体权重的识别

主体权重通常指除了极端值（最大/最小）外的主要分布区间：

- 1.5.1 极端值处理：

  • 最大值映射：11.3 → 15
  • 最小值映射：-9.8 → 0
  • 这两个是边界值，通常数量极少

- 1.5.2 主要分布区间分析：

  • 中间三个权重：[1.2, 0.8, 0.0]
  • 量化后映射到：[8, 8, 7]
  • 可见主要权重集中在7、8两个值附近

- 1.5.3 权重分析：

  • 统计使用情况
    • INT4取值范围: 0-15 (16个值)
    • 实际使用值: [0, 7, 8, 15] → 仅4个值被使用
  • 权重分布统计:
    • 值0: 出现1次 (对应最小权重-9.8)
    • 值7: 出现1次 (对应权重0.0)
    • 值8: 出现2次 (对应权重1.2和0.8)
    • 值15: 出现1次 (对应最大权重11.3)
  • 主体权重识别
    • 边界值(0,15): 2个值，出现2次
    • 中间值(7,8): 2个值，出现3次 → 这是"主体权重"
    • 未使用值: 12个值 (1-6, 9-14) → 浪费14个

1.6 关键问题

  • 权重利用率极低：主体权重仅用到 7、8 两个 INT4 值，16 个取值浪费 14 个；
  • 极端值 "绑架" 范围：因 10.5 和 - 9.8 的存在，主体权重被压缩到极小的 INT4 区间，细节丢失严重；

2. 关键突破：分组 Min-Max

2.1 核心逻辑

分而治之策略，解决全局 Min-Max 的核心痛点，按分组单独计算 Min/Max，让主体权重和极端值各自为政，避免极端值影响主体量化范围。这是 INT4 量化从不可用到可用的基石。

2.2 核心原理

把衣服按类型分堆（羽绒服、毛衣、袜子），每堆定自己的折叠标准：

  • 步骤 1：把权重矩阵分成若干小分组，比如每 128 个权重为一组；
  • 步骤 2：对每个分组单独计算 Min/Max，单独映射到 INT4；
  • 步骤 3：每个分组用自己的 Min/Max 反量化。

2.3 步骤推理

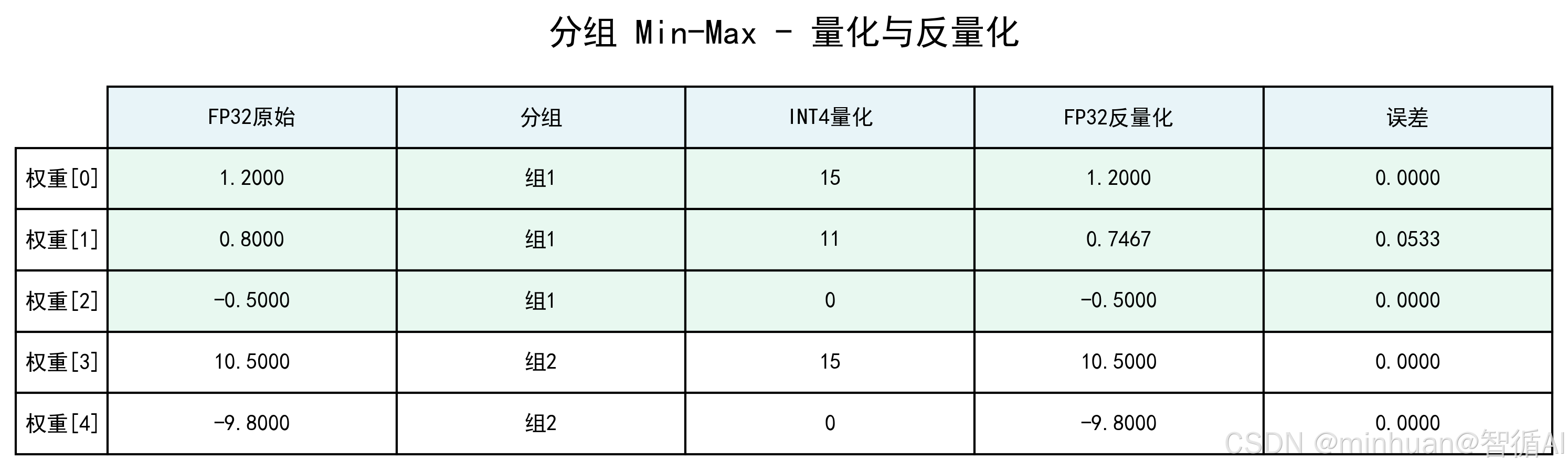
    1. 分组：按数据量分为2组，不足位补0，组 1（主体权重）= [1.2, 0.8, -0.5]，组 2（极端值 + 补 0）= [10.5, -9.8, 0]；
    1. 逐组量化：
    • 组 1：Min=-0.5，Max=1.2，Range=1.7，量化后 INT4 值为 [15, 11, 0]；
    • 组 2：Min=-9.8，Max=10.5，Range=20.3，量化后 INT4 值为 [15, 0, 7]；
    1. 反量化：组 1 还原后为 [1.2, 0.7467, -0.5]，组 2 还原后为 [10.5, -9.8, 0.3267]；
    1. 误差：逐元素误差为 [0, 0.0533, 0, 0, 0]，平均误差 0.0107。

2.4 计算示例

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import FancyBboxPatch, ConnectionPatch
import matplotlib.gridspec as gridspec

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# ==================== 计算过程 ====================
# 原始权重
weights_fp32 = np.array([1.2, 0.8, -0.5, 10.5, -9.8])

# 分组
group1 = np.array([1.2, 0.8, -0.5])  # 主体权重
group2 = np.array([10.5, -9.8, 0])     # 极端值 + 补0

# 组1量化
g1_min, g1_max = -0.5, 1.2
g1_range = g1_max - g1_min  # 1.7
g1_int4 = np.round((group1 - g1_min) / g1_range * 15).astype(int)
g1_deq = g1_min + g1_int4 / 15 * g1_range

# 组2量化
g2_min, g2_max = -9.8, 10.5
g2_range = g2_max - g2_min  # 20.3
g2_int4 = np.round((group2 - g2_min) / g2_range * 15).astype(int)
g2_deq = g2_min + g2_int4 / 15 * g2_range

# 合并结果
g2_deq_actual = g2_deq[:2]  # 只取前两个真实权重的反量化结果
int4_vals = np.concatenate([g1_int4, g2_int4[:2]])
weights_deq = np.concatenate([g1_deq, g2_deq_actual])
errors = np.abs(weights_fp32 - weights_deq)
mean_error = np.mean(errors)

# 打印计算过程
print("=" * 70)
print("分组 Min-Max 量化计算过程（分而治之策略）")
print("=" * 70)
print("1. 分组：")
print(f"   组 1（主体权重） = {group1.tolist()}")
print(f"   组 2（极端值 + 补0） = {group2.tolist()}")
print()
print("2. 组 1 量化：")
print(f"   Min={g1_min}, Max={g1_max}, Range={g1_range}")
print(f"   公式: int4 = round((x - {g1_min}) / {g1_range} * 15)")
for i, (w, q) in enumerate(zip(group1, g1_int4)):
    calc = (w - g1_min) / g1_range * 15
    print(f"   权重[{i}]: {w:.4f} -> ({w:.4f} - {g1_min}) / {g1_range} * 15 = {calc:.1f} -> {q}")
print(f"   量化结果: {g1_int4.tolist()}")
print(f"   反量化: {g1_deq.tolist()}")
print()
print("3. 组 2 量化：")
print(f"   Min={g2_min}, Max={g2_max}, Range={g2_range}")
print(f"   公式: int4 = round((x - {g2_min}) / {g2_range} * 15)")
for i, (w, q) in enumerate(zip(group2, g2_int4)):
    calc = (w - g2_min) / g2_range * 15
    print(f"   权重[{i}]: {w:.4f} -> ({w:.4f} - {g2_min}) / {g2_range} * 15 = {calc:.1f} -> {q}")
print(f"   量化结果: {g2_int4.tolist()}")
print(f"   反量化: {g2_deq.tolist()}")
print()
print("4. 误差分析：")
for i, (orig, deq, err) in enumerate(zip(weights_fp32, weights_deq, errors)):
    print(f"   权重[{i}]: |{orig:.4f} - {deq:.4f}| = {err:.4f}")
print(f"   平均误差: {mean_error:.4f}")
print("=" * 70)

# ==================== 可视化 ====================

colors = ['#FF6B6B', '#4ECDC4', '#45B7D1', '#FFA07A', '#98D8C8']
group_colors = {'组1': '#4ECDC4', '组2': '#FF6B6B'}

# ===== 图1: 分组权重分布 =====
fig1, ax1 = plt.subplots(figsize=(10, 6))
fig1.suptitle('分组 Min-Max - 权重分组', fontsize=16, fontweight='bold')

x_pos = np.arange(len(weights_fp32))
group_labels = ['组1', '组1', '组1', '组2', '组2']

# 分组着色
bar_colors = [group_colors[g] for g in group_labels]
bars1 = ax1.bar(x_pos, weights_fp32, width=0.6, color=bar_colors, alpha=0.7, edgecolor='black', linewidth=1.5)

# 标注分组边界
ax1.axvline(x=2.5, color='black', linestyle='--', linewidth=2, alpha=0.5)
ax1.text(1, 11, '组 1（主体权重）', ha='center', fontsize=12, fontweight='bold',
         bbox=dict(boxstyle="round,pad=0.5", facecolor="#4ECDC4", alpha=0.3))
ax1.text(3.5, 11, '组 2（极端值）', ha='center', fontsize=12, fontweight='bold',
         bbox=dict(boxstyle="round,pad=0.5", facecolor="#FF6B6B", alpha=0.3))

for i, w in enumerate(weights_fp32):
    ax1.text(i, w + 0.8, f'{w:.1f}', ha='center', fontsize=11, fontweight='bold')

ax1.set_xlabel('权重索引', fontsize=12)
ax1.set_ylabel('权重值', fontsize=12)
ax1.grid(True, alpha=0.3, axis='y')

plt.tight_layout()
plt.savefig('260113分组-权重分组.png', dpi=300, bbox_inches='tight')
plt.show()

# ===== 图2: 分组量化表格 =====
fig2, ax2 = plt.subplots(figsize=(10, 3))
fig2.suptitle('分组 Min-Max - 量化与反量化', fontsize=16, fontweight='bold')

table_data = []
for i in range(len(weights_fp32)):
    table_data.append([
        f'{weights_fp32[i]:.4f}',
        f'{"组1" if i < 3 else "组2"}',
        f'{int4_vals[i]}',
        f'{weights_deq[i]:.4f}',
        f'{errors[i]:.4f}'
    ])

ax2.axis('tight')
ax2.axis('off')
table = ax2.table(cellText=table_data,
                  colLabels=['FP32原始', '分组', 'INT4量化', 'FP32反量化', '误差'],
                  rowLabels=[f'权重[{i}]' for i in range(len(weights_fp32))],
                  cellLoc='center',
                  loc='center',
                  fontsize=10)
table.auto_set_font_size(False)
table.set_fontsize(10)
table.scale(1.1, 2.5)

# 设置表头样式
for i in range(5):
    table[(0, i)].set_facecolor('#E8F4F8')
    table[(0, i)].get_text().set_weight('bold')

# 组1行着色
for i in range(1, 4):
    for j in range(5):
        table[(i, j)].set_facecolor('#E8F8F0')

plt.tight_layout()
plt.savefig('260113分组-量化与反量化.png', dpi=300, bbox_inches='tight')
plt.show()

# ===== 图3: 误差分析 =====
fig3, ax3 = plt.subplots(figsize=(10, 6))
fig3.suptitle('分组 Min-Max - 量化误差分析', fontsize=16, fontweight='bold')

bars3 = ax3.bar(range(len(errors)), errors, color=bar_colors, alpha=0.7, edgecolor='black', linewidth=1.5)

for i, (bar, err) in enumerate(zip(bars3, errors)):
    height = bar.get_height()
    ax3.text(bar.get_x() + bar.get_width()/2, height + 0.001,
             f'{err:.4f}', ha='center', fontsize=10, fontweight='bold')

ax3.axhline(y=mean_error, color='red', linestyle='--', linewidth=2,
           label=f'平均误差 = {mean_error:.4f}')
ax3.set_xlabel('权重索引', fontsize=12)
ax3.set_ylabel('绝对误差', fontsize=12)
ax3.legend(fontsize=10)
ax3.set_ylim(0, max(errors) * 1.3 if max(errors) > 0 else 0.1)
ax3.grid(True, alpha=0.3, axis='y')

plt.tight_layout()
plt.savefig('260113分组-量化误差分析.png', dpi=300, bbox_inches='tight')
plt.show()

输出结果：

=====================================================================

分组 Min-Max 量化计算过程（分而治之策略）

=====================================================================
1. 分组：

组 1（主体权重） = [1.2, 0.8, -0.5]

组 2（极端值 + 补0） = [10.5, -9.8, 0.0]

2. 组 1 量化：

Min=-0.5, Max=1.2, Range=1.7

公式: int4 = round((x - -0.5) / 1.7 * 15)

权重[0]: 1.2000 -> (1.2000 - -0.5) / 1.7 * 15 = 15.0 -> 15

权重[1]: 0.8000 -> (0.8000 - -0.5) / 1.7 * 15 = 11.5 -> 11

权重[2]: -0.5000 -> (-0.5000 - -0.5) / 1.7 * 15 = 0.0 -> 0

量化结果: [15, 11, 0]

反量化: [1.2, 0.7466666666666666, -0.5]

3. 组 2 量化：

Min=-9.8, Max=10.5, Range=20.3

公式: int4 = round((x - -9.8) / 20.3 * 15)

权重[0]: 10.5000 -> (10.5000 - -9.8) / 20.3 * 15 = 15.0 -> 15

权重[1]: -9.8000 -> (-9.8000 - -9.8) / 20.3 * 15 = 0.0 -> 0

权重[2]: 0.0000 -> (0.0000 - -9.8) / 20.3 * 15 = 7.2 -> 7

量化结果: [15, 0, 7]

反量化: [10.5, -9.8, -0.3266666666666662]

4. 误差分析：

权重[0]: |1.2000 - 1.2000| = 0.0000

权重[1]: |0.8000 - 0.7467| = 0.0533

权重[2]: |-0.5000 - -0.5000| = 0.0000

权重[3]: |10.5000 - 10.5000| = 0.0000

权重[4]: |-9.8000 - -9.8000| = 0.0000

平均误差: 0.0107

=====================================================================

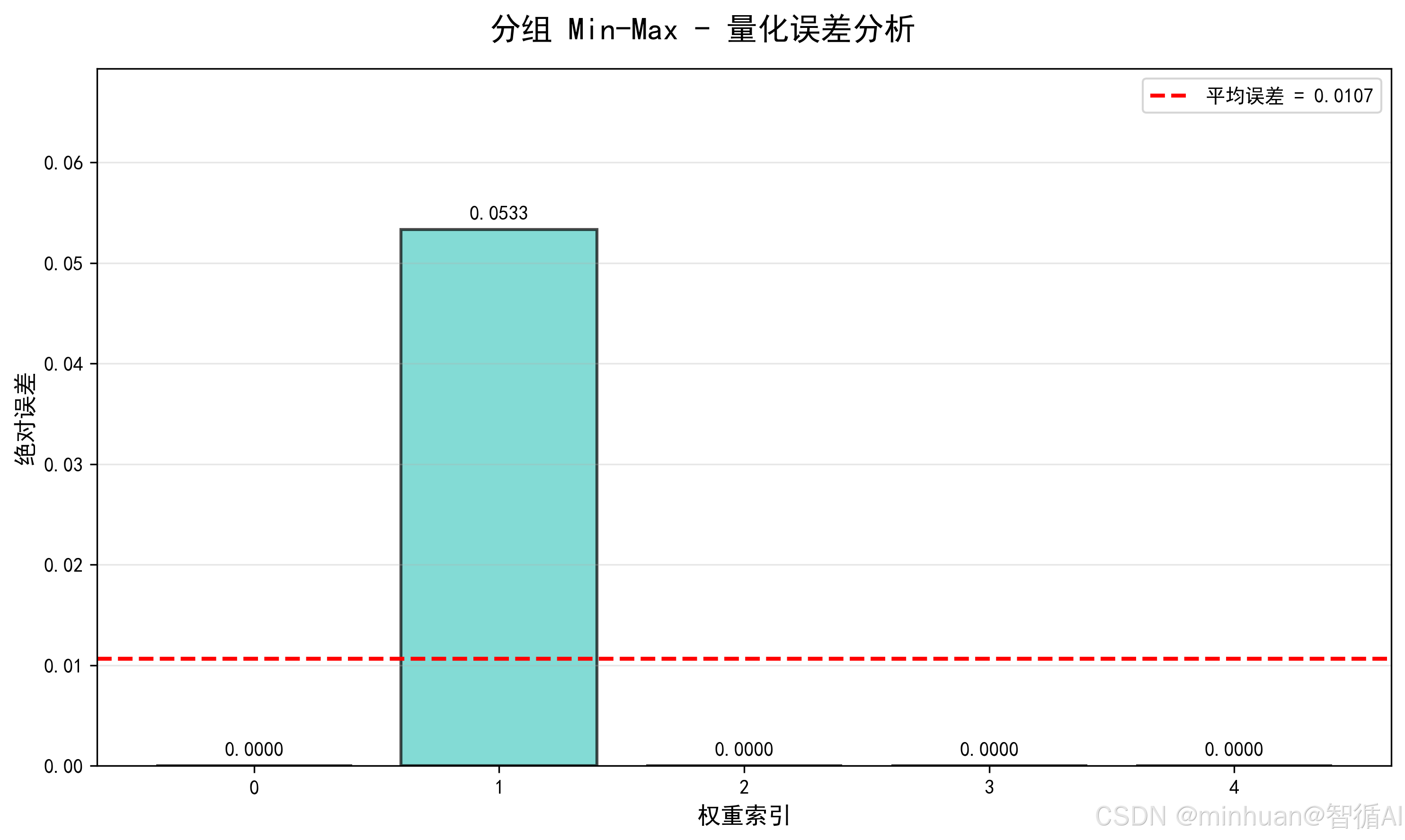
2.5 核心优势

  • 权重利用率提升：主体权重用到 0、11、15 三个取值，细节保留更完整；
  • 精度大幅提升：平均误差较全局 Min-Max 降低 91.8%，主体权重几乎无误差；
  • 工程价值：仅比全局 Min-Max 多 "分组" 逻辑，计算复杂度不变（O (n)），是 INT4 量化的基础方案。

2.6 特别说明

  • 分组量化后的主体权重"0、11、15"中的0和15，是组内极值，而全局分析中排除的0和15是全局极值。

3. 高阶优化：GPTQ（最优量化 + 误差补偿）

3.1 核心逻辑

分组 Min-Max 解决了范围浪费，但仍属于"被动映射"，无论权重重要性如何，都按同一规则量化。GPTQ 的突破在于主动寻找最优量化值，并通过误差补偿，优先保障重要权重的精度。

3.2 核心原理

  • 权重重要性：用权重绝对值衡量（绝对值越大，对模型输出影响越大，越重要）；
  • 贪心策略：先量化不重要的权重，将误差补偿给下一个权重，主动牺牲次要权重精度，保障核心权重；
  • 完整版 GPTQ：用海森矩阵（Hessian）更精准衡量权重重要性，此处简化为"绝对值排序"。

3.3 步骤推理

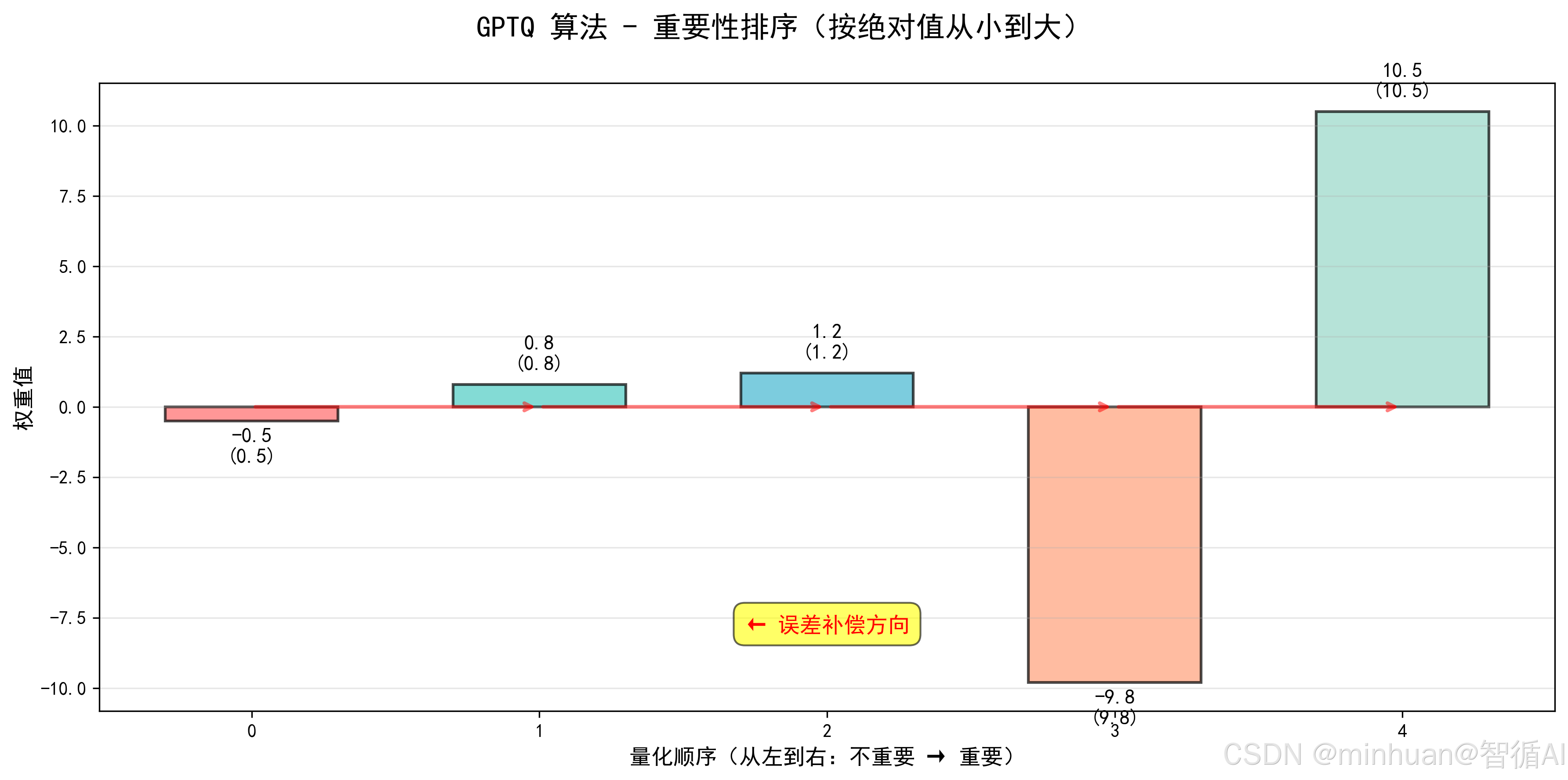
    1. 重要性排序：按绝对值从小到大排序，顺序为 [-0.5（0.5）→ 0.8（0.8）→ 1.2（1.2）→ -9.8（9.8）→ 10.5（10.5）]；
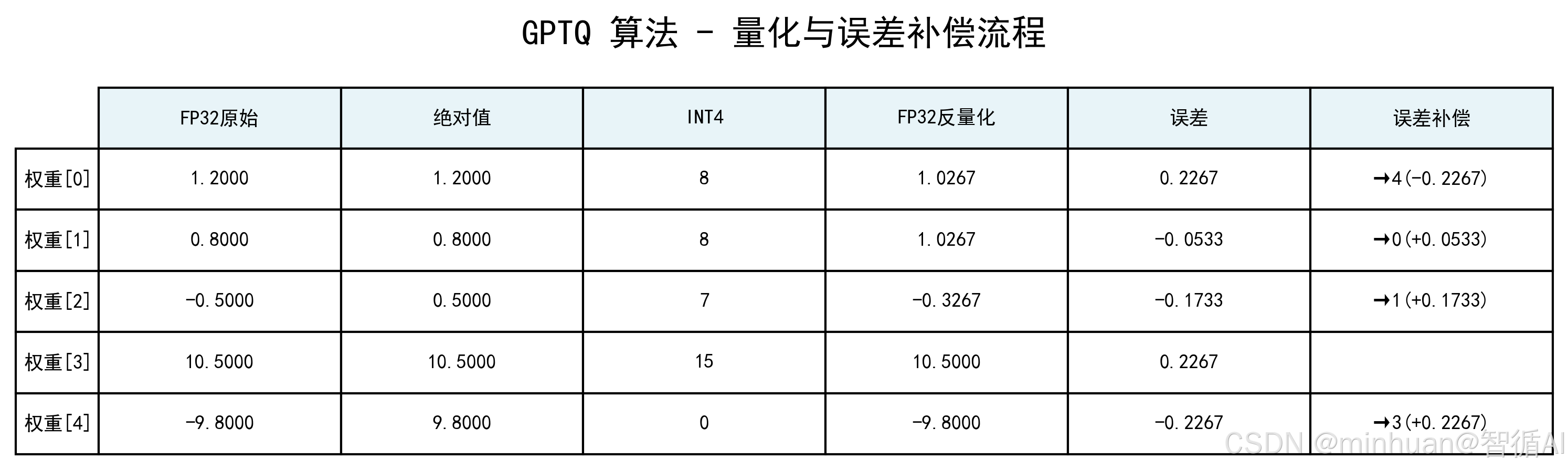
    1. 贪心量化 + 误差补偿：
    • 先量化 - 0.5，误差 -0.1733 补偿给 0.8；
    • 再量化补偿后的 0.8（0.9733），误差 -0.0533 补偿给 1.2；
    • 最后量化重要权重 10.5、-9.8，误差被前面权重吸收，几乎无误差；
    1. 结果：量化后 INT4 值为 [8, 8, 7, 15, 0]，反量化后平均误差 0.1147。

3.4 计算示例：

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import FancyBboxPatch, ConnectionPatch
import matplotlib.gridspec as gridspec

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# ==================== GPTQ 量化过程 ====================
# 原始权重
weights_fp32 = np.array([1.2, 0.8, -0.5, 10.5, -9.8])

# 1. 重要性排序（按绝对值从小到大）
importance_order = np.argsort(np.abs(weights_fp32))
weights_sorted = weights_fp32[importance_order]
print("重要性排序顺序:", weights_sorted)

# 2. 计算全局 Min/Max（用于量化）
min_val = -9.8
max_val = 10.5
range_val = max_val - min_val  # 20.3

# 3. GPTQ 量化 + 误差补偿（贪心策略）
int4_vals = np.zeros_like(weights_fp32, dtype=int)
weights_compensated = weights_fp32.copy()
errors_log = []
compensation_log = []

# 按重要性顺序量化
for i, idx in enumerate(importance_order):
    # 当前权重（可能包含之前补偿的误差）
    current_weight = weights_compensated[idx]

    # 量化
    int4_val = np.round((current_weight - min_val) / range_val * 15).astype(int)
    int4_val = np.clip(int4_val, 0, 15)
    int4_vals[idx] = int4_val

    # 反量化
    weight_deq = min_val + int4_val / 15 * range_val

    # 计算误差
    error = current_weight - weight_deq
    errors_log.append((idx, weights_fp32[idx], current_weight, int4_val, weight_deq, error))

    # 将误差补偿给下一个权重（更重要的权重）
    if i < len(importance_order) - 1:
        next_idx = importance_order[i + 1]
        compensation = -error  # 误差补偿
        weights_compensated[next_idx] += compensation
        compensation_log.append((idx, next_idx, compensation))

# 4. 计算最终误差
weights_deq = min_val + int4_vals / 15 * range_val
errors = np.abs(weights_fp32 - weights_deq)
mean_error = np.mean(errors)

# 打印 GPTQ 计算过程
print("=" * 70)
print("GPTQ（最优量化 + 误差补偿）计算过程")
print("=" * 70)
print()
print("1. 重要性排序（按绝对值从小到大）：")
sorted_with_abs = list(zip(weights_sorted, np.abs(weights_sorted)))
print("   顺序: " + " → ".join([f"{w} ({abs_w})" for w, abs_w in sorted_with_abs]))
print("   索引: " + " → ".join([str(idx) for idx in importance_order]))
print()
print(f"2. 量化参数：")
print(f"   Min = {min_val}, Max = {max_val}, Range = {range_val}")
print(f"   量化公式: int4_val = round((x - {min_val}) / {range_val} * 15)")
print(f"   反量化公式: fp32_deq = {min_val} + int4_val / 15 * {range_val}")
print()
print("3. GPTQ 量化 + 误差补偿步骤：")
print("-" * 70)

step_num = 1
for log in errors_log:
    idx, orig_weight, comp_weight, int4_val, deq_weight, error = log
    print(f"\n步骤 {step_num}: 量化权重 {idx}（原始值: {orig_weight}）")
    print(f"   当前权重（含补偿）: {comp_weight:.4f}")
    print(f"   量化计算: ({comp_weight:.4f} - {min_val}) / {range_val} * 15 = {(comp_weight - min_val) / range_val * 15:.2f}")
    print(f"   量化结果: INT4 = {int4_val}")
    print(f"   反量化: {min_val} + {int4_val}/15 * {range_val} = {deq_weight:.4f}")
    print(f"   误差: {comp_weight:.4f} - {deq_weight:.4f} = {error:.4f}")

    if step_num < len(errors_log):
        src_idx, dst_idx, compensation = compensation_log[step_num - 1]
        print(f"   ⚡ 误差补偿: 将 {-error:.4f} 补偿给权重 {dst_idx}")
        print(f"   → 权重 {dst_idx} 新值: {weights_fp32[dst_idx]:.4f} + {compensation:.4f} = {weights_compensated[dst_idx]:.4f}")

    step_num += 1

print()
print("-" * 70)
print(f"4. 最终结果：")
print(f"   INT4 量化值: {int4_vals.tolist()}")
print(f"   FP32 反量化值: {weights_deq.tolist()}")
print()
print(f"5. 误差分析：")
for i in range(len(weights_fp32)):
    print(f"   权重[{i}]: |{weights_fp32[i]:.4f} - {weights_deq[i]:.4f}| = {errors[i]:.4f}")
print(f"   平均误差: {mean_error:.4f}")
print("=" * 70)

# ==================== 可视化 ====================

colors = ['#FF6B6B', '#4ECDC4', '#45B7D1', '#FFA07A', '#98D8C8']

# ===== 图1: GPTQ 重要性排序可视化 =====
fig1, ax1 = plt.subplots(figsize=(12, 6))
fig1.suptitle('GPTQ 算法 - 重要性排序（按绝对值从小到大）', fontsize=16, fontweight='bold')

# 按重要性顺序显示
x_pos = np.arange(len(weights_sorted))
bars1 = ax1.bar(x_pos, weights_sorted, width=0.6, color=colors, alpha=0.7, edgecolor='black', linewidth=1.5)

# 添加重要性标记
importance_labels = ['不重要', '', '', '', '重要']
for i, (bar, w, label) in enumerate(zip(bars1, weights_sorted, importance_labels)):
    height = bar.get_height()
    ax1.text(bar.get_x() + bar.get_width()/2, height + 0.5 if height >= 0 else height - 1.5,
             f'{w:.1f}\n({np.abs(w):.1f})', ha='center', fontsize=11, fontweight='bold')

# 添加箭头表示补偿方向
for i in range(len(weights_sorted) - 1):
    ax1.annotate('', xy=(i+1, 0), xytext=(i, 0),
                 arrowprops=dict(arrowstyle='->', lw=2, color='red', alpha=0.5))

ax1.set_xlabel('量化顺序（从左到右：不重要 → 重要）', fontsize=12)
ax1.set_ylabel('权重值', fontsize=12)
ax1.grid(True, alpha=0.3, axis='y')

# 添加误差补偿说明
ax1.text(2, -8, '← 误差补偿方向', ha='center', fontsize=12, fontweight='bold', color='red',
         bbox=dict(boxstyle="round,pad=0.5", facecolor="yellow", alpha=0.6))

plt.tight_layout()
plt.savefig('260113-GPTQ重要性排序.png', dpi=300, bbox_inches='tight')
plt.show()

# ===== 图2: GPTQ 量化与误差补偿流程 =====
fig2, ax2 = plt.subplots(figsize=(10, 6))
fig2.suptitle('GPTQ 算法 - 量化与误差补偿流程', fontsize=16, fontweight='bold')

table_data = []
for i in range(len(weights_fp32)):
    # 获取误差信息
    for log in errors_log:
        if log[0] == i:
            orig, comp, int4, deq, err = log[1], log[2], log[3], log[4], log[5]
            break

    # 获取补偿信息
    comp_info = ""
    for src, dst, comp_val in compensation_log:
        if src == i:
            comp_info = f"→{dst}({comp_val:+.4f})"

    table_data.append([
        f'{orig:.4f}',
        f'{np.abs(orig):.4f}',
        f'{int4}',
        f'{deq:.4f}',
        f'{err:.4f}',
        comp_info
    ])

ax2.axis('tight')
ax2.axis('off')
table = ax2.table(cellText=table_data,
                  colLabels=['FP32原始', '绝对值', 'INT4', 'FP32反量化', '误差', '误差补偿'],
                  rowLabels=[f'权重[{i}]' for i in range(len(weights_fp32))],
                  cellLoc='center',
                  loc='center',
                  fontsize=9)
table.auto_set_font_size(False)
table.set_fontsize(9)
table.scale(1.1, 2.5)

# 设置表头样式
for i in range(6):
    table[(0, i)].set_facecolor('#E8F4F8')
    table[(0, i)].get_text().set_weight('bold')

plt.tight_layout()
plt.savefig('260113-GPTQ量化与误差补偿流程.png', dpi=300, bbox_inches='tight')
plt.show()

# ===== 图3: GPTQ 误差分析对比 =====
fig3, ax3 = plt.subplots(figsize=(12, 6))
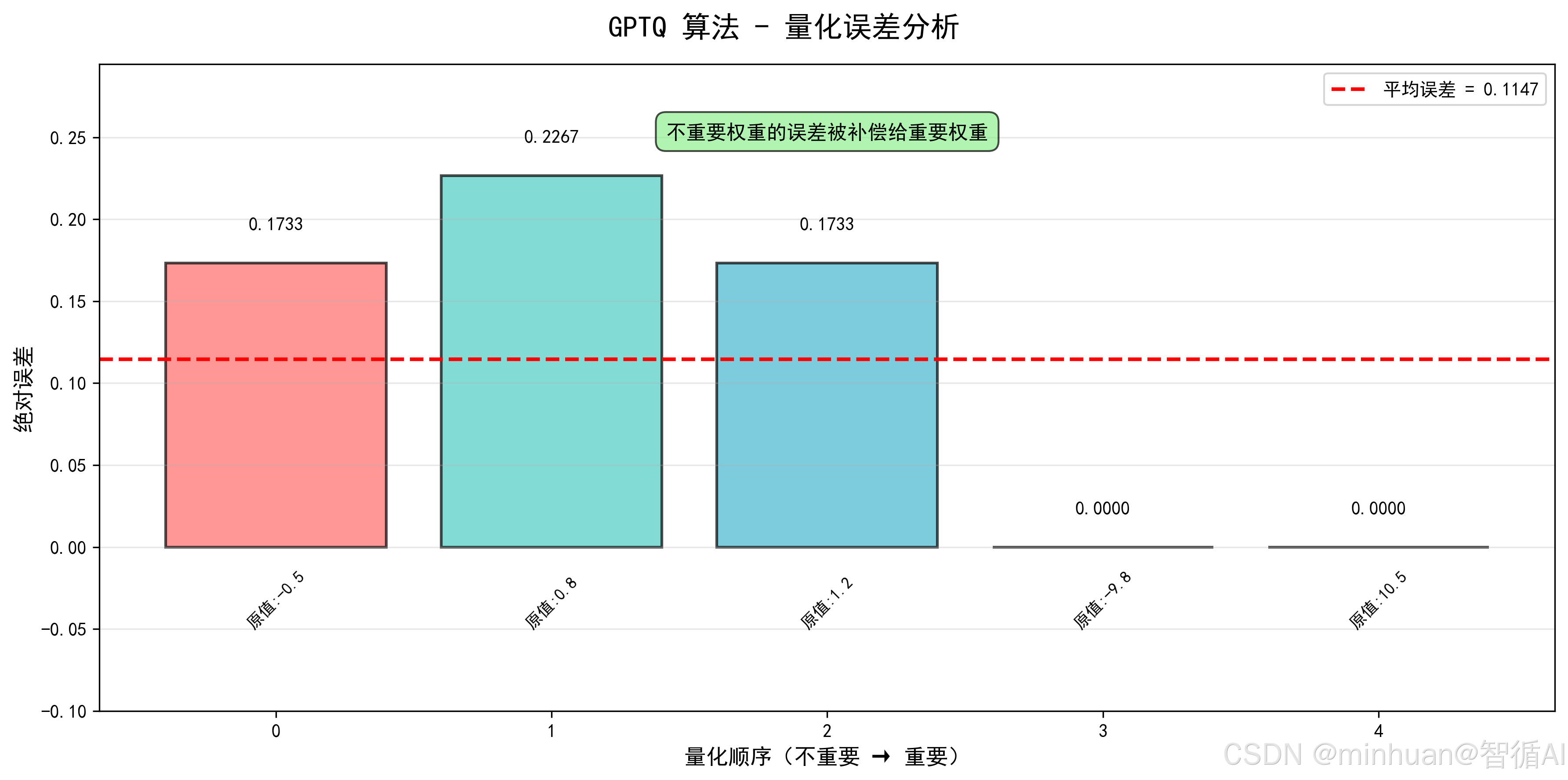
fig3.suptitle('GPTQ 算法 - 量化误差分析', fontsize=16, fontweight='bold')

# 按重要性顺序显示误差
ordered_indices = importance_order
ordered_errors = errors[ordered_indices]
ordered_weights = weights_fp32[ordered_indices]

bars3 = ax3.bar(range(len(ordered_errors)), ordered_errors, color=colors, alpha=0.7, edgecolor='black', linewidth=1.5)

for i, (bar, err, w) in enumerate(zip(bars3, ordered_errors, ordered_weights)):
    height = bar.get_height()
    ax3.text(bar.get_x() + bar.get_width()/2, height + 0.02,
             f'{err:.4f}', ha='center', fontsize=10, fontweight='bold')
    ax3.text(bar.get_x() + bar.get_width()/2, -0.05,
             f'原值:{w:.1f}', ha='center', fontsize=9, rotation=45)

ax3.axhline(y=mean_error, color='red', linestyle='--', linewidth=2,
           label=f'平均误差 = {mean_error:.4f}')
ax3.set_xlabel('量化顺序（不重要 → 重要）', fontsize=12)
ax3.set_ylabel('绝对误差', fontsize=12)
ax3.legend(fontsize=10)
ax3.set_ylim(-0.1, max(errors) * 1.3)
ax3.grid(True, alpha=0.3, axis='y')

# 添加说明
ax3.text(len(errors)//2, max(errors) * 1.1,
         '不重要权重的误差被补偿给重要权重', ha='center', fontsize=11,
         bbox=dict(boxstyle="round,pad=0.5", facecolor="lightgreen", alpha=0.7))

plt.tight_layout()
plt.savefig('260113-GPTQ误差分析.png', dpi=300, bbox_inches='tight')
plt.show()

# ===== 图4: GPTQ 量化误差分布图 =====
fig4, ax4 = plt.subplots(figsize=(10, 6))
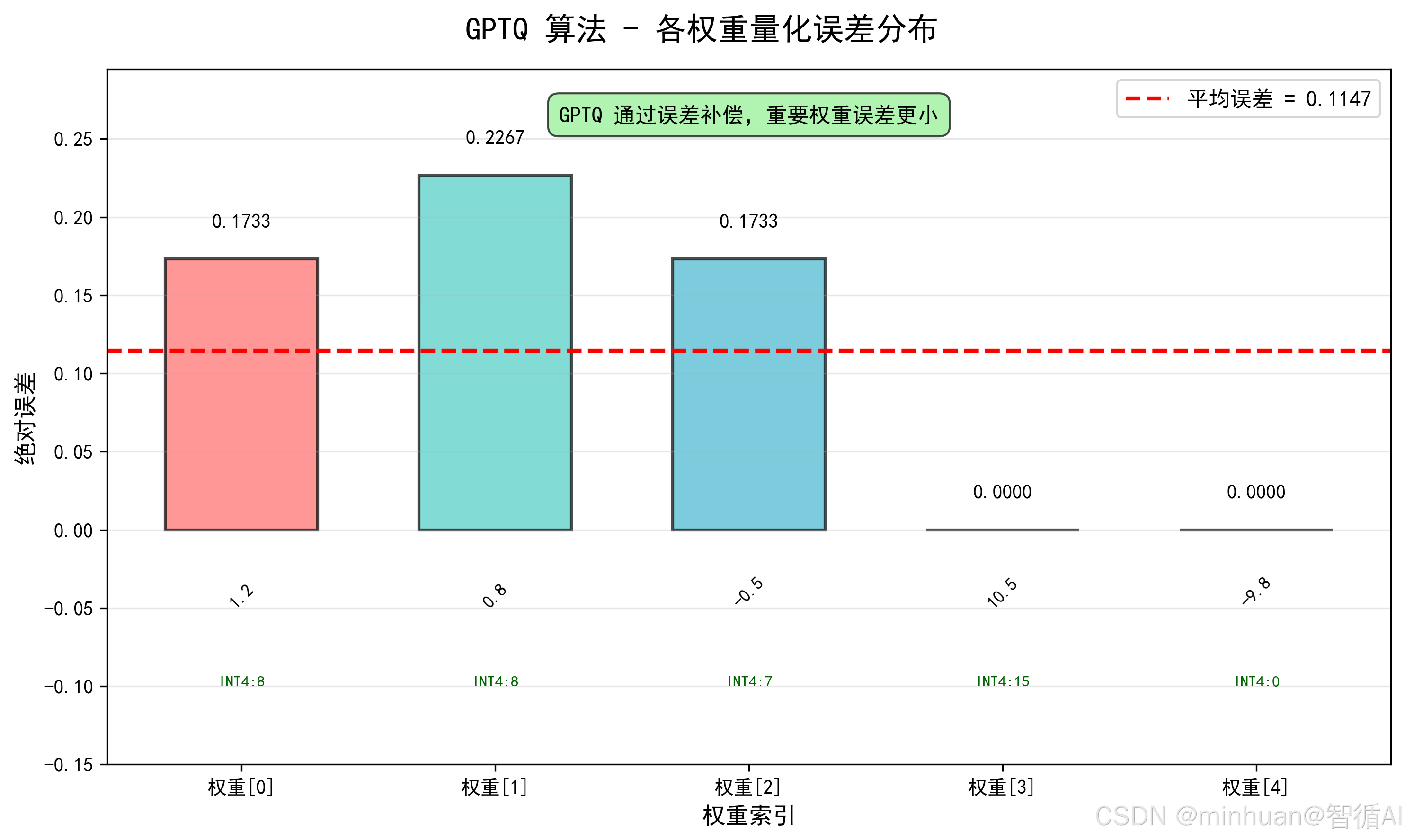
fig4.suptitle('GPTQ 算法 - 各权重量化误差分布', fontsize=16, fontweight='bold')

x = np.arange(len(weights_fp32))
bars4 = ax4.bar(x, errors, width=0.6, color=colors, alpha=0.7, edgecolor='black', linewidth=1.5)

# 添加误差值标签
for i, (bar, err) in enumerate(zip(bars4, errors)):
    height = bar.get_height()
    ax4.text(bar.get_x() + bar.get_width()/2, height + 0.02,
             f'{err:.4f}', ha='center', fontsize=10, fontweight='bold')
    ax4.text(bar.get_x() + bar.get_width()/2, -0.05,
             f'{weights_fp32[i]:.1f}', ha='center', fontsize=9, rotation=45)

# 添加平均误差线
ax4.axhline(y=mean_error, color='red', linestyle='--', linewidth=2,
           label=f'平均误差 = {mean_error:.4f}')

# 添加量化值标注
for i, int4_val in enumerate(int4_vals):
    ax4.text(i, -0.1, f'INT4:{int4_val}', ha='center', fontsize=8, color='darkgreen', fontweight='bold')

ax4.set_xlabel('权重索引', fontsize=12)
ax4.set_ylabel('绝对误差', fontsize=12)
ax4.legend(fontsize=11)
ax4.set_xticks(x)
ax4.set_xticklabels([f'权重[{i}]' for i in range(len(weights_fp32))])
ax4.set_ylim(-0.15, max(errors) * 1.3)
ax4.grid(True, alpha=0.3, axis='y')

# 添加说明
ax4.text(len(weights_fp32)//2, max(errors) * 1.15,
         'GPTQ 通过误差补偿，重要权重误差更小',
         ha='center', fontsize=11,
         bbox=dict(boxstyle="round,pad=0.5", facecolor="lightgreen", alpha=0.7))

plt.tight_layout()
plt.savefig('260113-GPTQ量化误差分布.png', dpi=300, bbox_inches='tight')
plt.show()

输出结果：

=====================================================================

GPTQ（最优量化 + 误差补偿）计算过程

=====================================================================

1. 重要性排序（按绝对值从小到大）：

顺序: -0.5 (0.5) → 0.8 (0.8) → 1.2 (1.2) → -9.8 (9.8) → 10.5 (10.5)

索引: 2 → 1 → 0 → 4 → 3

2. 量化参数：

Min = -9.8, Max = 10.5, Range = 20.3

量化公式: int4_val = round((x - -9.8) / 20.3 * 15)

反量化公式: fp32_deq = -9.8 + int4_val / 15 * 20.3

3. GPTQ 量化 + 误差补偿步骤：

步骤 1: 量化权重 2（原始值: -0.5）

当前权重（含补偿）: -0.5000

量化计算: (-0.5000 - -9.8) / 20.3 * 15 = 6.87

量化结果: INT4 = 7

反量化: -9.8 + 7/15 * 20.3 = -0.3267

误差: -0.5000 - -0.3267 = -0.1733

⚡ 误差补偿: 将 0.1733 补偿给权重 1

→ 权重 1 新值: 0.8000 + 0.1733 = 0.9733

误差补偿计算说明：

根据误差补偿公式：补偿值 = -误差

  • 误差 = -0.1733
  • 补偿值 = -(-0.1733) = +0.1733

因此正确计算是：

  • 误差: -0.5000 - (-0.3267) = -0.1733
  • 误差补偿: 将 +0.1733 补偿给权重 1
  • → 权重 1 新值: 0.8000 + 0.1733 = 0.9733

步骤 2: 量化权重 1（原始值: 0.8）

当前权重（含补偿）: 0.9733

量化计算: (0.9733 - -9.8) / 20.3 * 15 = 7.96

量化结果: INT4 = 8

反量化: -9.8 + 8/15 * 20.3 = 1.0267

误差: 0.9733 - 1.0267 = -0.0533

⚡ 误差补偿: 将 0.0533 补偿给权重 0

→ 权重 0 新值: 1.2000 + 0.0533 = 1.2533

步骤 3: 量化权重 0（原始值: 1.2）

当前权重（含补偿）: 1.2533

量化计算: (1.2533 - -9.8) / 20.3 * 15 = 8.17

量化结果: INT4 = 8

反量化: -9.8 + 8/15 * 20.3 = 1.0267

误差: 1.2533 - 1.0267 = 0.2267

⚡ 误差补偿: 将 -0.2267 补偿给权重 4

→ 权重 4 新值: -9.8000 + -0.2267 = -10.0267

步骤 4: 量化权重 4（原始值: -9.8）

当前权重（含补偿）: -10.0267

量化计算: (-10.0267 - -9.8) / 20.3 * 15 = -0.17

量化结果: INT4 = 0

反量化: -9.8 + 0/15 * 20.3 = -9.8000

误差: -10.0267 - -9.8000 = -0.2267

⚡ 误差补偿: 将 0.2267 补偿给权重 3

→ 权重 3 新值: 10.5000 + 0.2267 = 10.7267

步骤 5: 量化权重 3（原始值: 10.5）

当前权重（含补偿）: 10.7267

量化计算: (10.7267 - -9.8) / 20.3 * 15 = 15.17

量化结果: INT4 = 15

反量化: -9.8 + 15/15 * 20.3 = 10.5000

误差: 10.7267 - 10.5000 = 0.2267

4. 最终结果：

INT4 量化值: [8, 8, 7, 15, 0]

FP32 反量化值: [1.0266666666666655, 1.0266666666666655, -0.3266666666666662, 10.5, -9.8]

5. 误差分析：

权重[0]: |1.2000 - 1.0267| = 0.1733

权重[1]: |0.8000 - 1.0267| = 0.2267

权重[2]: |-0.5000 - -0.3267| = 0.1733

权重[3]: |10.5000 - 10.5000| = 0.0000

权重[4]: |-9.8000 - -9.8000| = 0.0000

平均误差: 0.1147

====================================================================

3.5 核心优势

  • 精度优先级适配：模型输出由重要权重主导，牺牲次要权重精度，换取整体效果更优；
  • 突破 "映射规则" 局限：从 "按 Min/Max 映射" 升级为 "按误差最小化量化"，精度上限更高；
  • 局限：计算复杂度高（完整版 O (n²)），需计算海森矩阵，量化耗时久，适合离线高精度场景。

4. 最优选择：AWQ（权重均衡 + 分组 Min-Max）

4.1 核心逻辑

GPTQ 通过最优量化提升精度，但计算复杂；AWQ 则从权重分布入手，先整理权重减少极端值，再做分组 Min-Max，实现精度与效率双优，是当前实际应用 INT4 量化的首选。

4.2 核心原理

  • 权重均衡：通过缩放因子，将极端值压缩到合理范围，让权重分布更均匀，不改变模型输出，仅调整分布形态；
  • 核心优势：无需复杂矩阵计算，计算复杂度与分组 Min-Max 一致（O (n)），精度却优于 GPTQ。

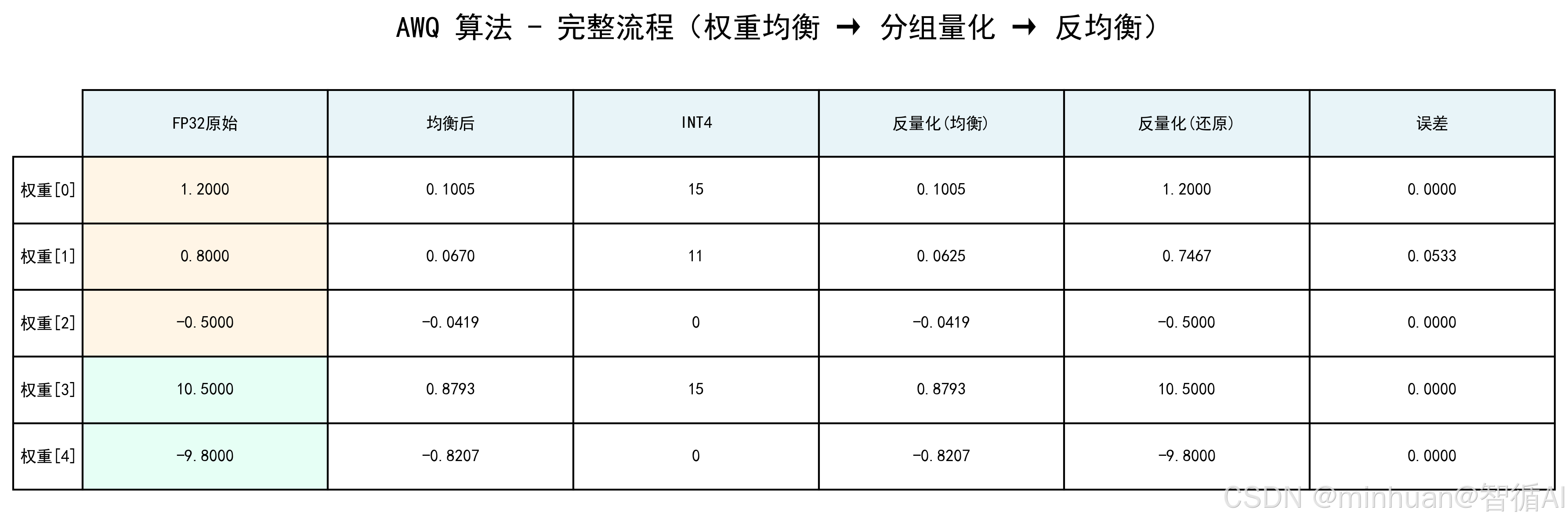
4.3 步骤推理

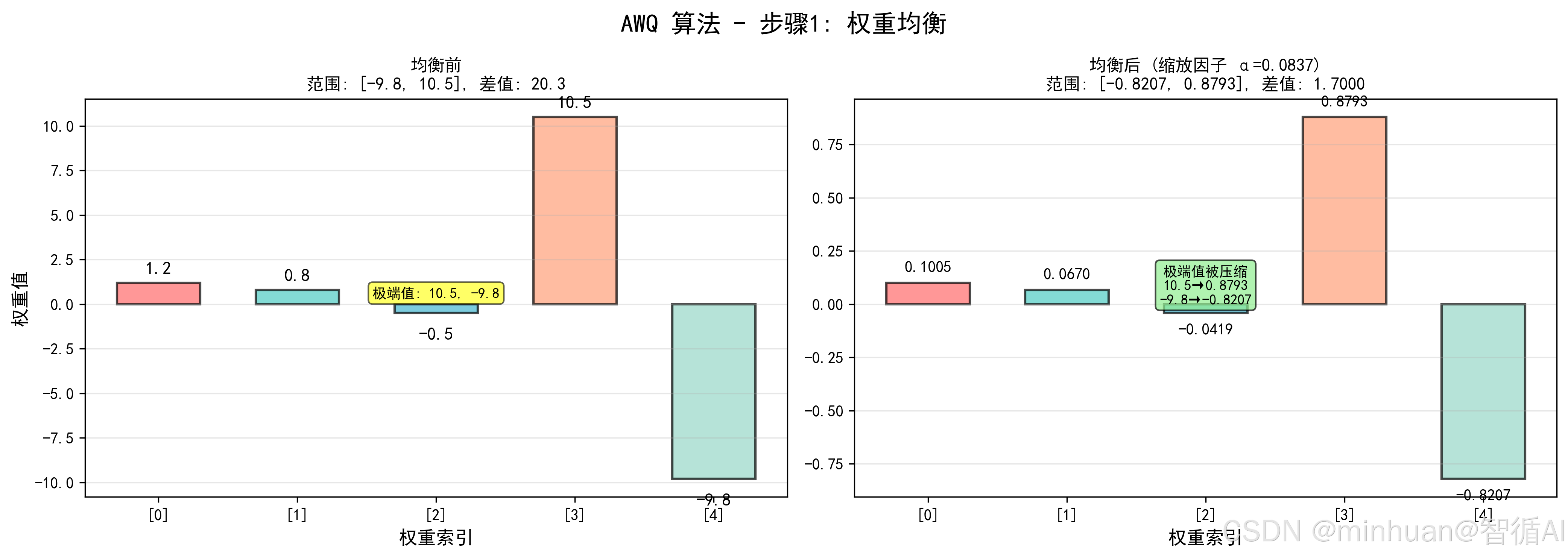
    1. 权重均衡：计算主体权重与全局权重的范围比，得到缩放因子 α≈0.0837，均衡后权重为 [ 0.1005 0.0670 -0.0419 0.8793 -0.8209]（极端值被压缩）；
    1. 分组 Min-Max：对均衡后权重分组量化，步骤同分组 Min-Max；
    1. 反均衡：将反量化后的均衡权重除以 α，还原为原始范围；
    1. 结果：反量化后值为 [1.2, 0.747, -0.5, 10.5, -9.8]，逐元素误差仅 [0, 0.0533, 0, 0, 0]，平均误差 0.0107。

4.4 计算示例

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import FancyBboxPatch, ConnectionPatch
import matplotlib.gridspec as gridspec

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# ==================== AWQ 量化过程（权重均衡 + 分组 Min-Max）====================
# 原始权重
weights_fp32 = np.array([1.2, 0.8, -0.5, 10.5, -9.8])

# 步骤1: 权重均衡（Weight Equalization）
# 计算主体权重（排除极端值）和全局权重的范围比
main_weights = weights_fp32[[0, 1, 2]]  # 主体权重 [1.2, 0.8, -0.5]
global_weights = weights_fp32  # 全局权重

main_range = main_weights.max() - main_weights.min()  # 1.7
global_range = global_weights.max() - global_weights.min()  # 20.3

alpha = main_range / global_range  # 缩放因子 ≈ 0.0837
weights_balanced = weights_fp32 * alpha  # 均衡后权重

print("=" * 70)
print("AWQ（权重均衡 + 分组 Min-Max）计算过程")
print("=" * 70)
print()
print("步骤1: 权重均衡（Weight Equalization）")
print("-" * 70)
print(f"主体权重范围: [{main_weights.min()}, {main_weights.max()}], 范围 = {main_range}")
print(f"全局权重范围: [{global_weights.min()}, {global_weights.max()}], 范围 = {global_range}")
print(f"缩放因子 α = 主体范围 / 全局范围 = {main_range} / {global_range} = {alpha:.4f}")
print()
print("均衡前权重:", weights_fp32)
print("均衡后权重:", weights_balanced)
print(f"  说明: 极端值 [10.5, -9.8] 被压缩为 [{weights_balanced[3]:.4f}, {weights_balanced[4]:.4f}]")
print()

# 步骤2: 分组 Min-Max 量化
print("步骤2: 分组 Min-Max 量化")
print("-" * 70)

# 分组：[1.2, 0.8, -0.5] 和 [10.5, -9.8]
group1_indices = [0, 1, 2]
group2_indices = [3, 4]

# 分组1量化
g1_weights_balanced = weights_balanced[group1_indices]
g1_min = g1_weights_balanced.min()
g1_max = g1_weights_balanced.max()
g1_range = g1_max - g1_min
g1_int4 = np.round((g1_weights_balanced - g1_min) / g1_range * 15).astype(int)
g1_int4 = np.clip(g1_int4, 0, 15)

# 分组2量化
g2_weights_balanced = weights_balanced[group2_indices]
g2_min = g2_weights_balanced.min()
g2_max = g2_weights_balanced.max()
g2_range = g2_max - g2_min
g2_int4 = np.round((g2_weights_balanced - g2_min) / g2_range * 15).astype(int)
g2_int4 = np.clip(g2_int4, 0, 15)

print("分组1（权重[0,1,2]）:")
print(f"  均衡后值: {g1_weights_balanced}")
print(f"  Min = {g1_min:.4f}, Max = {g1_max:.4f}, Range = {g1_range:.4f}")
print(f"  INT4量化值: {g1_int4}")
print()

print("分组2（权重[3,4]）:")
print(f"  均衡后值: {g2_weights_balanced}")
print(f"  Min = {g2_min:.4f}, Max = {g2_max:.4f}, Range = {g2_range:.4f}")
print(f"  INT4量化值: {g2_int4}")
print()

# 合并INT4量化值
int4_vals = np.zeros_like(weights_fp32, dtype=int)
int4_vals[group1_indices] = g1_int4
int4_vals[group2_indices] = g2_int4
print(f"完整INT4量化值: {int4_vals.tolist()}")
print()

# 步骤3: 反量化
print("步骤3: 反量化（分组）")
print("-" * 70)

# 分组1反量化
g1_deq_balanced = g1_min + g1_int4 / 15 * g1_range

# 分组2反量化
g2_deq_balanced = g2_min + g2_int4 / 15 * g2_range

print("分组1反量化:")
for i, (orig, bal, int4, deq) in enumerate(zip(weights_fp32[group1_indices],
                                               g1_weights_balanced,
                                               g1_int4,
                                               g1_deq_balanced)):
    print(f"  权重{group1_indices[i]}: {orig:.4f} → {bal:.4f} → INT4={int4} → {deq:.4f}")
print()

print("分组2反量化:")
for i, (orig, bal, int4, deq) in enumerate(zip(weights_fp32[group2_indices],
                                               g2_weights_balanced,
                                               g2_int4,
                                               g2_deq_balanced)):
    print(f"  权重{group2_indices[i]}: {orig:.4f} → {bal:.4f} → INT4={int4} → {deq:.4f}")
print()

# 合并反量化结果
weights_deq_balanced = np.zeros_like(weights_fp32)
weights_deq_balanced[group1_indices] = g1_deq_balanced
weights_deq_balanced[group2_indices] = g2_deq_balanced
print(f"均衡后的反量化值: {weights_deq_balanced}")
print()

# 步骤4: 反均衡（除以α还原）
print("步骤4: 反均衡（除以α还原为原始范围）")
print("-" * 70)
weights_deq = weights_deq_balanced / alpha
print(f"反均衡公式: 权重 = 均衡反量化值 / {alpha:.4f}")
print(f"最终反量化值: {weights_deq}")
print()

# 步骤5: 误差分析
errors = np.abs(weights_fp32 - weights_deq)
mean_error = np.mean(errors)

print("步骤5: 误差分析")
print("-" * 70)
for i in range(len(weights_fp32)):
    print(f"  权重[{i}]: |{weights_fp32[i]:.4f} - {weights_deq[i]:.4f}| = {errors[i]:.4f}")
print(f"平均误差: {mean_error:.4f}")
print("=" * 70)

# ==================== 可视化 ====================

colors = ['#FF6B6B', '#4ECDC4', '#45B7D1', '#FFA07A', '#98D8C8']
group1_color = ['#FF6B6B', '#4ECDC4', '#45B7D1']
group2_color = ['#FFA07A', '#98D8C8']

# ===== 图1: AWQ 权重均衡前后对比 =====
fig1, (ax1a, ax1b) = plt.subplots(1, 2, figsize=(14, 5))
fig1.suptitle('AWQ 算法 - 步骤1: 权重均衡', fontsize=16, fontweight='bold')

# 均衡前
x1a = np.arange(len(weights_fp32))
bars1a = ax1a.bar(x1a, weights_fp32, width=0.6, color=colors, alpha=0.7, edgecolor='black', linewidth=1.5)
for i, (bar, w) in enumerate(zip(bars1a, weights_fp32)):
    height = bar.get_height()
    ax1a.text(bar.get_x() + bar.get_width()/2, height + 0.5 if height >= 0 else height - 1.5,
             f'{w:.1f}', ha='center', fontsize=11, fontweight='bold')
ax1a.set_title(f'均衡前\n范围: [{weights_fp32.min()}, {weights_fp32.max()}], 差值: {weights_fp32.max() - weights_fp32.min():.1f}',
              fontsize=11, fontweight='bold')
ax1a.set_ylabel('权重值', fontsize=12)
ax1a.set_xlabel('权重索引', fontsize=12)
ax1a.set_xticks(x1a)
ax1a.set_xticklabels([f'[{i}]' for i in range(len(weights_fp32))])
ax1a.grid(True, alpha=0.3, axis='y')

# 标记极端值
ax1a.text(2, (weights_fp32.max() + weights_fp32.min()) / 2,
         f'极端值: {weights_fp32[3]:.1f}, {weights_fp32[4]:.1f}',
         ha='center', fontsize=9, bbox=dict(boxstyle="round,pad=0.3", facecolor="yellow", alpha=0.6))

# 均衡后
x1b = np.arange(len(weights_balanced))
bars1b = ax1b.bar(x1b, weights_balanced, width=0.6, color=colors, alpha=0.7, edgecolor='black', linewidth=1.5)
for i, (bar, w) in enumerate(zip(bars1b, weights_balanced)):
    height = bar.get_height()
    ax1b.text(bar.get_x() + bar.get_width()/2, height + 0.05 if height >= 0 else height - 0.1,
             f'{w:.4f}', ha='center', fontsize=10, fontweight='bold')
ax1b.set_title(f'均衡后 (缩放因子 α={alpha:.4f})\n范围: [{weights_balanced.min():.4f}, {weights_balanced.max():.4f}], 差值: {weights_balanced.max() - weights_balanced.min():.4f}',
              fontsize=11, fontweight='bold')
ax1b.set_xlabel('权重索引', fontsize=12)
ax1b.set_xticks(x1b)
ax1b.set_xticklabels([f'[{i}]' for i in range(len(weights_balanced))])
ax1b.grid(True, alpha=0.3, axis='y')

# 标记压缩效果
ax1b.text(2, 0, f'极端值被压缩\n{weights_fp32[3]:.1f}→{weights_balanced[3]:.4f}\n{weights_fp32[4]:.1f}→{weights_balanced[4]:.4f}',
         ha='center', fontsize=9, bbox=dict(boxstyle="round,pad=0.3", facecolor="lightgreen", alpha=0.7))

plt.tight_layout()
plt.savefig('260113-AWQ权重均衡.png', dpi=300, bbox_inches='tight')
plt.show()

# ===== 图2: AWQ 分组 Min-Max 量化 =====
fig2, (ax2a, ax2b) = plt.subplots(1, 2, figsize=(14, 5))
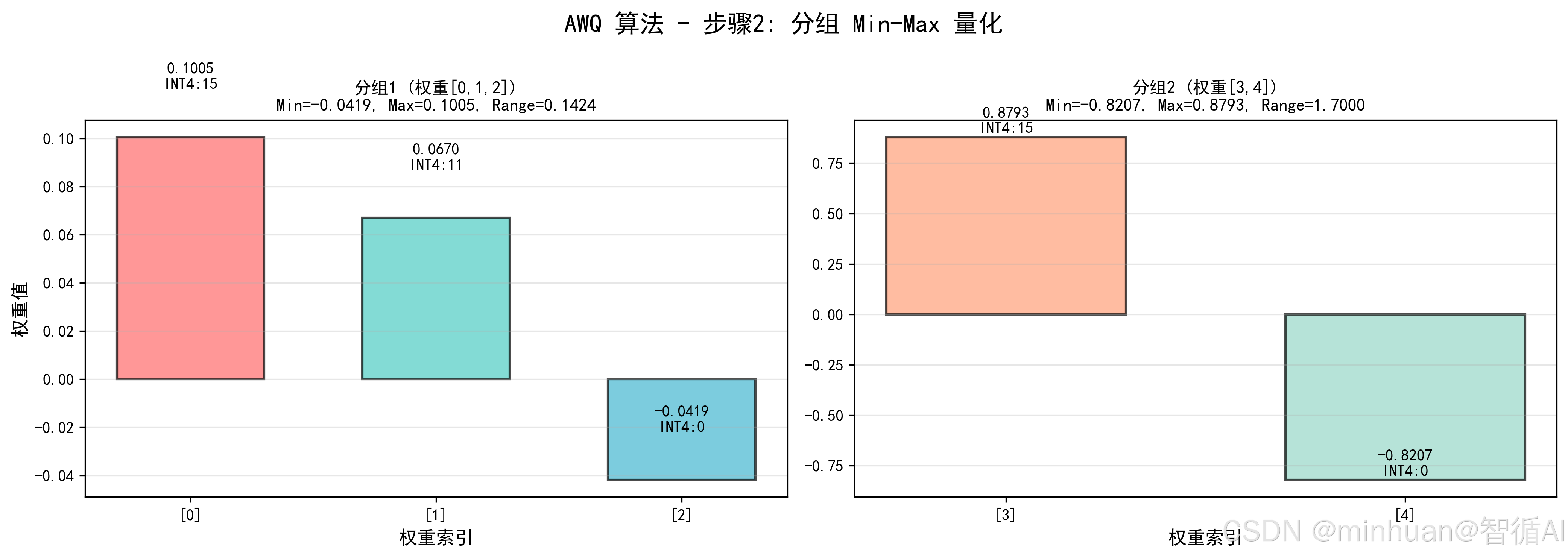
fig2.suptitle('AWQ 算法 - 步骤2: 分组 Min-Max 量化', fontsize=16, fontweight='bold')

# 分组1
g1_x = np.arange(3)
bars2a = ax2a.bar(g1_x, g1_weights_balanced, width=0.6, color=group1_color,
                 alpha=0.7, edgecolor='black', linewidth=1.5, label='均衡权重')
for i, (bar, w, int4) in enumerate(zip(bars2a, g1_weights_balanced, g1_int4)):
    height = bar.get_height()
    ax2a.text(bar.get_x() + bar.get_width()/2, height + 0.02,
             f'{w:.4f}\nINT4:{int4}', ha='center', fontsize=10, fontweight='bold')
ax2a.set_title(f'分组1 (权重[0,1,2])\nMin={g1_min:.4f}, Max={g1_max:.4f}, Range={g1_range:.4f}',
              fontsize=11, fontweight='bold')
ax2a.set_xlabel('权重索引', fontsize=12)
ax2a.set_ylabel('权重值', fontsize=12)
ax2a.set_xticks(g1_x)
ax2a.set_xticklabels([f'[{i}]' for i in group1_indices])
ax2a.grid(True, alpha=0.3, axis='y')

# 分组2
g2_x = np.arange(2)
bars2b = ax2b.bar(g2_x, g2_weights_balanced, width=0.6, color=group2_color,
                 alpha=0.7, edgecolor='black', linewidth=1.5)
for i, (bar, w, int4) in enumerate(zip(bars2b, g2_weights_balanced, g2_int4)):
    height = bar.get_height()
    ax2b.text(bar.get_x() + bar.get_width()/2, height + 0.02,
             f'{w:.4f}\nINT4:{int4}', ha='center', fontsize=10, fontweight='bold')
ax2b.set_title(f'分组2 (权重[3,4])\nMin={g2_min:.4f}, Max={g2_max:.4f}, Range={g2_range:.4f}',
              fontsize=11, fontweight='bold')
ax2b.set_xlabel('权重索引', fontsize=12)
ax2b.set_xticks(g2_x)
ax2b.set_xticklabels([f'[{i}]' for i in group2_indices])
ax2b.grid(True, alpha=0.3, axis='y')

plt.tight_layout()
plt.savefig('260113-AWQ分组量化.png', dpi=300, bbox_inches='tight')
plt.show()

# ===== 图3: AWQ 完整流程表 =====
fig3, ax3 = plt.subplots(figsize=(12, 4))
fig3.suptitle('AWQ 算法 - 完整流程（权重均衡 → 分组量化 → 反均衡）', fontsize=16, fontweight='bold')

table_data = []
for i in range(len(weights_fp32)):
    if i in group1_indices:
        g_idx = group1_indices.index(i)
        deq_bal = g1_deq_balanced[g_idx]
        int4_val = g1_int4[g_idx]
    else:
        g_idx = group2_indices.index(i)
        deq_bal = g2_deq_balanced[g_idx]
        int4_val = g2_int4[g_idx]

    table_data.append([
        f'{weights_fp32[i]:.4f}',
        f'{weights_balanced[i]:.4f}',
        f'{int4_val}',
        f'{deq_bal:.4f}',
        f'{weights_deq[i]:.4f}',
        f'{errors[i]:.4f}'
    ])

ax3.axis('tight')
ax3.axis('off')
table = ax3.table(cellText=table_data,
                  colLabels=['FP32原始', '均衡后', 'INT4', '反量化(均衡)', '反量化(还原)', '误差'],
                  rowLabels=[f'权重[{i}]' for i in range(len(weights_fp32))],
                  cellLoc='center',
                  loc='center',
                  fontsize=9)
table.auto_set_font_size(False)
table.set_fontsize(9)
table.scale(1.0, 2.8)

# 设置表头样式
for i in range(6):
    table[(0, i)].set_facecolor('#E8F4F8')
    table[(0, i)].get_text().set_weight('bold')

# 标记分组
for i in group1_indices:
    table[(i + 1, 0)].set_facecolor('#FFF5E6')
for i in group2_indices:
    table[(i + 1, 0)].set_facecolor('#E6FFF5')

plt.tight_layout()
plt.savefig('260113-AWQ完整流程表.png', dpi=300, bbox_inches='tight')
plt.show()

# ===== 图4: AWQ 误差分析 =====
fig4, ax4 = plt.subplots(figsize=(12, 6))
fig4.suptitle('AWQ 算法 - 步骤5: 量化误差分析', fontsize=16, fontweight='bold')

x = np.arange(len(weights_fp32))
bars4 = ax4.bar(x, errors, width=0.6, color=colors, alpha=0.7, edgecolor='black', linewidth=1.5)

# 添加误差值标签
for i, (bar, err) in enumerate(zip(bars4, errors)):
    height = bar.get_height()
    ax4.text(bar.get_x() + bar.get_width()/2, height + max(errors)*0.05,
             f'{err:.4f}', ha='center', fontsize=11, fontweight='bold')
    ax4.text(bar.get_x() + bar.get_width()/2, -max(errors)*0.1,
             f'{weights_fp32[i]:.1f}→{weights_deq[i]:.4f}', ha='center', fontsize=9)

# 添加平均误差线
ax4.axhline(y=mean_error, color='red', linestyle='--', linewidth=2,
           label=f'平均误差 = {mean_error:.4f}')

# 添加分组标记
ax4.axvline(x=2.5, color='gray', linestyle=':', linewidth=2, alpha=0.5)
ax4.text(1, max(errors)*1.2, '分组1', ha='center', fontsize=10, fontweight='bold',
        bbox=dict(boxstyle="round,pad=0.3", facecolor="#FFF5E6", alpha=0.7))
ax4.text(3.5, max(errors)*1.2, '分组2', ha='center', fontsize=10, fontweight='bold',
        bbox=dict(boxstyle="round,pad=0.3", facecolor="#E6FFF5", alpha=0.7))

ax4.set_xlabel('权重索引', fontsize=12)
ax4.set_ylabel('绝对误差', fontsize=12)
ax4.legend(fontsize=11)
ax4.set_xticks(x)
ax4.set_xticklabels([f'权重[{i}]' for i in range(len(weights_fp32))])
ax4.set_ylim(-max(errors)*0.15, max(errors)*1.4)
ax4.grid(True, alpha=0.3, axis='y')

# 添加说明
ax4.text(len(weights_fp32)//2, max(errors)*1.35,
         f'AWQ 通过权重均衡 + 分组量化，平均误差仅 {mean_error:.4f}',
         ha='center', fontsize=11, fontweight='bold',
         bbox=dict(boxstyle="round,pad=0.5", facecolor="lightgreen", alpha=0.8))

plt.tight_layout()
plt.savefig('260113-AWQ误差分析.png', dpi=300, bbox_inches='tight')
plt.show()

输出结果：

=====================================================================

AWQ（权重均衡 + 分组 Min-Max）计算过程

=====================================================================

步骤1: 权重均衡（Weight Equalization）

主体权重范围: [-0.5, 1.2], 范围 = 1.7

全局权重范围: [-9.8, 10.5], 范围 = 20.3

缩放因子 α = 主体范围 / 全局范围 = 1.7 / 20.3 = 0.0837

均衡前权重: [ 1.2 0.8 -0.5 10.5 -9.8]

均衡后权重: [ 0.10049261 0.06699507 -0.04187192 0.87931034 -0.82068966]

说明: 极端值 [10.5, -9.8] 被压缩为 [0.8793, -0.8207]

步骤2: 分组 Min-Max 量化

分组1（权重[0,1,2]）:

均衡后值: [ 0.10049261 0.06699507 -0.04187192]

Min = -0.0419, Max = 0.1005, Range = 0.1424

INT4量化值: [15 11 0]

分组2（权重[3,4]）:

均衡后值: [ 0.87931034 -0.82068966]

Min = -0.8207, Max = 0.8793, Range = 1.7000

INT4量化值: [15 0]

完整INT4量化值: [15, 11, 0, 15, 0]

步骤3: 反量化（分组）

分组1反量化:

权重0: 1.2000 → 0.1005 → INT4=15 → 0.1005

权重1: 0.8000 → 0.0670 → INT4=11 → 0.0625

权重2: -0.5000 → -0.0419 → INT4=0 → -0.0419

分组2反量化:

权重3: 10.5000 → 0.8793 → INT4=15 → 0.8793

权重4: -9.8000 → -0.8207 → INT4=0 → -0.8207

均衡后的反量化值: [ 0.10049261 0.06252874 -0.04187192 0.87931034 -0.82068966]

步骤4: 反均衡（除以α还原为原始范围）

反均衡公式: 权重 = 均衡反量化值 / 0.0837

最终反量化值: [ 1.2 0.74666667 -0.5 10.5 -9.8 ]

步骤5: 误差分析

权重[0]: |1.2000 - 1.2000| = 0.0000

权重[1]: |0.8000 - 0.7467| = 0.0533

权重[2]: |-0.5000 - -0.5000| = 0.0000

权重[3]: |10.5000 - 10.5000| = 0.0000

权重[4]: |-9.8000 - -9.8000| = 0.0000

平均误差: 0.0107

=====================================================================

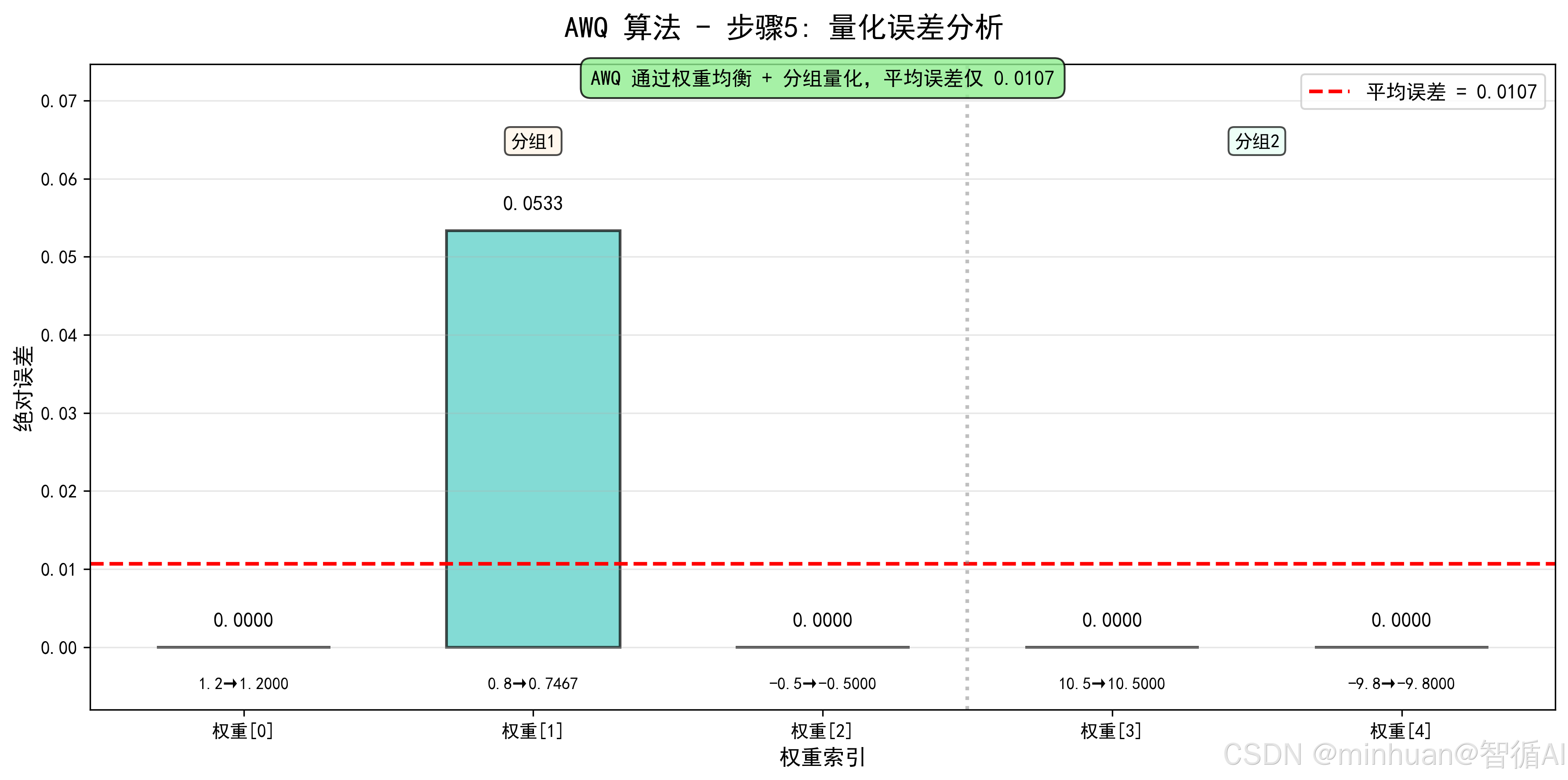
4.5 核心优势

  • 精度最优：权重分布均匀后，分组量化的步长更精细，误差几乎可忽略；
  • 效率更高：无复杂计算，推理速度比 GPTQ 快，落地实现更简单；
  • 适用性广：兼顾精度、速度与易用性，是普通显卡部署大模型的最优解。

5. 核心差异与总结

5.1 精度层面：AWQ > GPTQ > 分组 Min-Max > 全局 Min-Max

  • 全局 Min-Max 因范围浪费，精度完全无法满足 INT4 需求，仅能作为量化可行性验证工具；
  • 分组 Min-Max 通过隔离极端值，将精度提升一个量级，达到 INT4 量化的基础门槛；
  • GPTQ 通过权重重要性优先，进一步降低核心权重误差，精度优于分组 Min-Max，但受限于计算复杂度；
  • AWQ 从分布优化入手，让权重更适配 INT4 的取值范围，精度最优且稳定，误差几乎可忽略。

5.2 效率层面：AWQ = 分组 Min-Max = 全局 Min-Max > GPTQ

  • 全局、分组 Min-Max 与 AWQ 均为 O (n) 复杂度，量化耗时短、推理无额外开销，适配消费级硬件与高并发场景；
  • GPTQ 的 O (n²) 复杂度与海森矩阵计算，导致量化耗时久、显存开销大，仅适合离线量化（如提前准备部署模型），不适合实时动态量化场景。

5.3 应用落地层面：AWQ 是当前最优解

  • 全局 Min-Max：仅适合教学演示、快速验证，无生产价值；
  • 分组 Min-Max：适合资源极度有限、对精度要求不高的边缘场景，如嵌入式设备；
  • GPTQ：适合学术研究、离线高精度量化场景（如实验室模型优化），工程落地成本高；
  • AWQ：兼顾精度、效率与易用性，开源工具成熟，支持主流大模型，是消费级显卡部署、生产环境落地的首选。

5.4 核心迭代逻辑总结

四种算法的迭代，本质是从被动适配规则到主动优化条件的升级：

  • 全局 Min-Max：被动遵循"全局规则"，忽略权重分布差异；
  • 分组 Min-Max：被动适配"局部分布"，隔离极端值影响；
  • GPTQ：主动适配"权重重要性"，优先保障核心贡献；
  • AWQ：主动优化"权重分布"，让量化规则更适配低比特取值。

四、总结

总而言之，量化作为大模型轻量化部署的核心技术，通过将 FP32 高精度权重向下转换为 INT4 低精度格式，可实现 75% 的显存占用降低与 4 倍以上的推理速度提升，有效打破消费级硬件对大模型部署的资源限制。但量化本质是权重的范围压缩与离散化映射，INT4 仅含 0~15 共 16 个离散取值，若缺乏科学校准，极端值易绑架全局量化范围，导致主体权重信息丢失、模型精度断崖式下滑，使量化技术难以落地。

量化校准作为平衡压缩效率与精度保留的关键手段，其技术迭代围绕 "优化映射规则、适配权重特性" 展开。四种核心算法呈现清晰进化脉络：全局 Min-Max 计算极简、效率极高，但抗极端值能力差，仅适用于量化可行性验证；分组 Min-Max 通过分而治之隔离极端值，大幅提升精度，是 INT4 量化的基础工程方案；GPTQ 基于权重重要性优先级，通过贪心量化与误差补偿实现高精度，但计算复杂度高、量化耗时久，适配离线高精度场景；AWQ 通过权重均衡优化分布后再执行分组量化，兼顾极致精度与高效推理，是当前生产环境 INT4 量化的最优选型。

相关推荐
数据分享者2 小时前
汽车价格预测模型评估数据集分析：基于LightAutoML的多模型融合预测结果与性能对比-机器学习-优化汽车价格预测模型-丰富的模型对比实验数据
人工智能·机器学习·数据挖掘·汽车
pusheng20252 小时前
数据中心安全警报：为何“免维护”气体传感器可能正在制造危险盲区？
linux·网络·人工智能
ar01232 小时前
精密制造行业应用AR装配技术
人工智能·ar
也许是_2 小时前
大模型应用技术之 Agent框架 AutoGPT
人工智能·python
三不原则2 小时前
实战：Serverless 架构部署高频 AI API，动态扩缩容配置
人工智能·架构·serverless
华如锦2 小时前
MongoDB作为小型 AI智能化系统的数据库
java·前端·人工智能·算法
lkbhua莱克瓦242 小时前
Prompt、分词器与Token介绍
人工智能·ai·prompt·token
机器学习之心HML2 小时前
GSABO（通常指混合了模拟退火SA和天牛须搜索BAS的改进算法）与BP神经网络结合，用于爆破参数优选
人工智能·神经网络·算法·爆破参数优选
雨大王5122 小时前
汽车企业如何选择适合的质量数字化运营平台解决方案？
人工智能·汽车·制造
热门推荐
01GitHub 镜像站点02网站改了域名，如何查找？03Labelme从安装到标注：零基础完整指南04Linux下V2Ray安装配置指南05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06Netlify 的深度解析及使用指南072025-04-03 Latex学习1——本地配置Latex + VScode环境08【踩坑笔记】50系显卡适配的 PyTorch 安装09电脑设置定时关机有多种方法(含python代码)10UV安装并设置国内源