动态规划分类及算法实现

一、动态规划核心思想

动态规划（Dynamic Programming，DP）通过将复杂问题分解为重叠子问题，并存储子问题的解以避免重复计算，从而提高效率。其核心特点包括：

最优子结构：指的是一个问题的最优解包含其子问题的最优解
重叠子问题性质：指的是在求解子问题的过程中，有大量的子问题是重复的，一个子问题在下一阶段的决策中可能会被多次用到。如果有大量重复的子问题，那么只需要对其求解一次，然后用表格将结果存储下来，以后使用时可以直接查询，不需要再次求解。
状态转移方程：定义如何从子问题的解推导出原问题的解
无后效性： 指的是子问题的解（状态值）只与之前阶段有关，而与后面阶段无关。当前阶段的若干状态值一旦确定，就不再改变，不会再受到后续阶段决策的影响。

动态规划的核心思想：

把「原问题」分解为「若干个重叠的子问题」，每个子问题的求解过程都构成一个「阶段」。在完成一个阶段的计算之后，动态规划方法才会执行下一个阶段的计算。

在求解子问题的过程中，按照「自顶向下的记忆化搜索方法」或者「自底向上的递推方法」求解出「子问题的解」，把结果存储在表格中，当需要再次求解此子问题时，直接从表格中查询该子问题的解，从而避免了大量的重复计算。

这看起来很像是分治算法，但动态规划与分治算法的不同点在于：

适用于动态规划求解的问题，在分解之后得到的子问题往往是相互联系的，会出现若干个重叠子问题。

使用动态规划方法会将这些重叠子问题的解保存到表格里，供随后的计算查询使用，从而避免大量的重复计算。

二、动态规划分类体系

1. 按状态转移方式分类

类型	特点	典型问题
线性DP	状态沿线性顺序转移	最长递增子序列、最大子数组和
区间DP	状态定义在区间上	矩阵连乘、石子合并、回文划分
树形DP	在树结构上进行状态转移	树的最大独立集、二叉树盗贼
状态压缩DP	用二进制表示状态集合	旅行商问题、棋盘覆盖
数位DP	处理数字位上的计数问题	数字范围统计、含有特定数字的数
概率/期望DP	处理概率和期望值	游戏胜率、期望步数

2. 按问题类型分类

类型	特点	典型问题
背包问题	资源分配优化	0-1背包、完全背包、多重背包
序列问题	处理序列关系	LCS、编辑距离、最长回文子序列
路径问题	网格路径计数/优化	最小路径和、不同路径、地下城游戏
分割问题	将问题分割求解	钢条切割、单词拆分、完全平方数

2.动态规划的基本思路

如下图所示，我们在使用动态规划方法解决某些最优化问题时，可以将解决问题的过程按照一定顺序（时间顺序、空间顺序或其他顺序）分解为若干个相互联系的「阶段」。然后按照顺序对每一个阶段做出「决策」，这个决策既决定了本阶段的效益，也决定了下一阶段的初始状态。依次做完每个阶段的决策之后，就得到了一个整个问题的决策序列。

这样就将一个原问题分解为了一系列的子问题，再通过逐步求解从而获得最终结果。

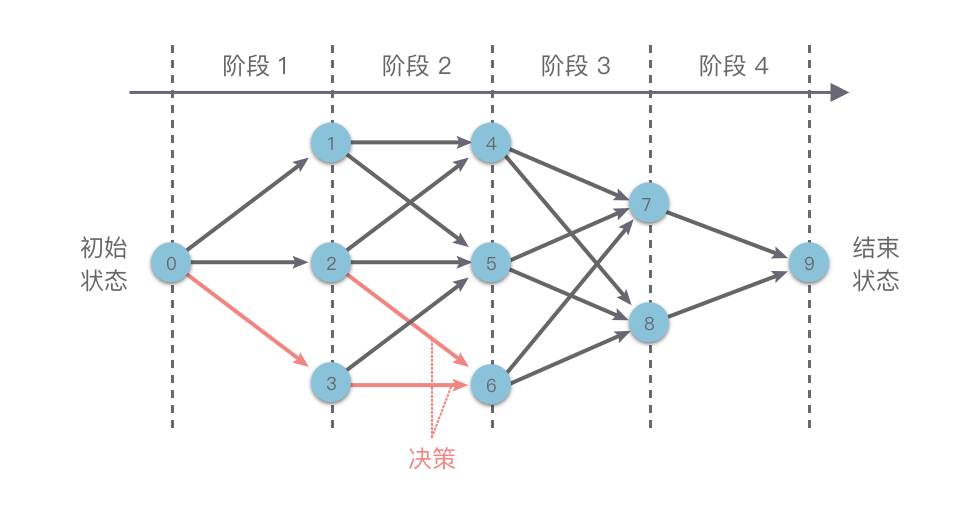
这种前后关联、具有链状结构的多阶段进行决策的问题也叫做「多阶段决策问题」。

通常我们使用动态规划方法来解决问题的基本思路如下：

阶段划分： 将原问题按顺序（时间顺序、空间顺序或其他顺序）分解为若干个相互联系的「阶段」。划分后的阶段⼀定是有序或可排序的，否则问题⽆法求解。

这里的「阶段」指的是⼦问题的求解过程。每个⼦问题的求解过程都构成⼀个「阶段」，在完成前⼀阶段的求解后才会进⾏后⼀阶段的求解。

定义状态：将和子问题相关的某些变量（位置、数量、体积、空间等等）作为一个「状态」表示出来。状态的选择要满⾜⽆后效性。

一个「状态」对应一个或多个子问题，所谓某个「状态」下的值，指的就是这个「状态」所对应的子问题的解。

状态转移：根据「上一阶段的状态」和「该状态下所能做出的决策」，推导出「下一阶段的状态」。或者说根据相邻两个阶段各个状态之间的关系，确定决策，然后推导出状态间的相互转移方式（即「状态转移方程」）。

初始条件和边界条件：根据问题描述、状态定义和状态转移方程，确定初始条件和边界条件。

最终结果：确定问题的求解目标，然后按照一定顺序求解每一个阶段的问题。最后根据状态转移方程的递推结果，确定最终结果。

三、经典算法实现

1. 最长递增子序列 (Longest Increasing Subsequence, LIS)

问题描述：

给定一个整数数组 nums，找到其中最长严格递增子序列的长度。子序列不要求连续，但必须保持原数组中的相对顺序。

示例：

复制代码

输入: [10, 9, 2, 5, 3, 7, 101, 18]
输出: 4
解释: 最长递增子序列是 [2, 3, 7, 101] 或 [2, 3, 7, 18]，长度都是 4

算法实现：

python 复制代码

def lengthOfLIS(nums):
    """
    动态规划解法
    时间复杂度: O(n²)
    空间复杂度: O(n)
    
    状态定义: dp[i] 表示以 nums[i] 结尾的最长递增子序列长度
    状态转移: dp[i] = max(dp[j] + 1)，其中 0 ≤ j < i 且 nums[j] < nums[i]
    """
    if not nums:
        return 0
    
    n = len(nums)
    dp = [1] * n  # 每个元素自身构成长度为1的子序列
    
    for i in range(n):
        # 检查所有比nums[i]小的元素
        for j in range(i):
            if nums[i] > nums[j]:
                dp[i] = max(dp[i], dp[j] + 1)
    
    return max(dp)

# 测试
print(lengthOfLIS([10, 9, 2, 5, 3, 7, 101, 18]))  # 输出: 4

2. 矩阵连乘问题 (Matrix Chain Multiplication)

问题描述：

给定一系列矩阵 A₁, A₂, ..., Aₙ，其中矩阵 Aᵢ 的维度为 pᵢ₋₁ × pᵢ。找到计算矩阵连乘 A₁ × A₂ × ... × Aₙ 的最优计算顺序，使得总的标量乘法次数最少。

矩阵乘法的代价：两个维度为 m×n 和 n×p 的矩阵相乘需要 m×n×p 次标量乘法。

示例：

复制代码

输入: p = [10, 30, 5, 60]  # 表示3个矩阵：10×30, 30×5, 5×60
输出: 4500
解释: 最优计算顺序是 (A₁ × A₂) × A₃，代价为 10×30×5 + 10×5×60 = 1500 + 3000 = 4500

算法实现：

python 复制代码

def matrixChainOrder(p):
    """
    动态规划解法
    时间复杂度: O(n³)
    空间复杂度: O(n²)
    
    状态定义: dp[i][j] 表示计算矩阵 A[i]...A[j] 所需的最小乘法次数
    状态转移: dp[i][j] = min(dp[i][k] + dp[k+1][j] + p[i]*p[k+1]*p[j+1])，i ≤ k < j
    """
    n = len(p) - 1  # 矩阵个数
    dp = [[0] * n for _ in range(n)]
    
    # 初始化对角线（单个矩阵乘法次数为0）
    for i in range(n):
        dp[i][i] = 0
    
    # 按区间长度递增计算
    for length in range(2, n + 1):
        for i in range(n - length + 1):
            j = i + length - 1
            dp[i][j] = float('inf')
            
            # 尝试所有可能的分割点
            for k in range(i, j):
                cost = dp[i][k] + dp[k+1][j] + p[i] * p[k+1] * p[j+1]
                dp[i][j] = min(dp[i][j], cost)
    
    return dp[0][n-1]

# 测试
print(matrixChainOrder([10, 30, 5, 60]))  # 输出: 4500

3. 0-1背包问题 (0-1 Knapsack Problem)

问题描述：

给定 n 个物品和一个容量为 capacity 的背包。第 i 个物品的重量为 weights[i]，价值为 values[i]。每个物品只能选择一次 （要么放入背包，要么不放）。目标是选择一些物品放入背包，使得背包中物品的总价值最大，且总重量不超过背包容量。

示例：

复制代码

输入:
  weights = [2, 3, 4, 5]
  values = [3, 4, 5, 6]
  capacity = 8
  
输出: 10
解释: 选择物品1(重量2,价值3)和物品4(重量5,价值6)，总重量7，总价值9；
      或者选择物品2(重量3,价值4)和物品3(重量4,价值5)，总重量7，总价值9；
      最优解是选择物品1和物品3，总重量6，总价值10

算法实现：

python 复制代码

def knapsack_01(weights, values, capacity):
    """
    0-1背包问题动态规划解法
    时间复杂度: O(n×capacity)
    空间复杂度: O(capacity)
    
    状态定义: dp[w] 表示容量为 w 的背包能装的最大价值
    状态转移: dp[w] = max(dp[w], dp[w-weights[i]] + values[i]) 对于每个物品
    """
    n = len(weights)
    dp = [0] * (capacity + 1)
    
    # 遍历每个物品
    for i in range(n):
        # 逆序遍历容量，保证每个物品只被选一次
        for w in range(capacity, weights[i] - 1, -1):
            dp[w] = max(dp[w], dp[w - weights[i]] + values[i])
    
    return dp[capacity]

# 完全背包问题（物品可以无限次选择）
def knapsack_complete(weights, values, capacity):
    """
    完全背包问题
    与0-1背包的唯一区别：遍历容量时是正序而不是逆序
    """
    dp = [0] * (capacity + 1)
    
    for i in range(len(weights)):
        # 正序遍历容量，允许物品被多次选择
        for w in range(weights[i], capacity + 1):
            dp[w] = max(dp[w], dp[w - weights[i]] + values[i])
    
    return dp[capacity]

# 测试
weights = [2, 3, 4, 5]
values = [3, 4, 5, 6]
capacity = 8
print(knapsack_01(weights, values, capacity))  # 输出: 10

4. 二叉树盗贼问题 (House Robber III)

问题描述：

一个小偷发现了一个新的盗窃区域。这个区域只有一个入口，所有房屋排列成一棵二叉树。小偷不能盗窃两个直接相连的房屋（即父子节点不能同时被盗窃）。给定二叉树的根节点，计算小偷能偷到的最大金额。

示例：

复制代码

输入二叉树:
     3
    / \
   2   3
    \   \ 
     3   1
     
输出: 7
解释: 盗窃房屋 3 (根节点) + 3 + 1 = 7
      或者盗窃房屋 2 + 3 (右子节点) = 5
      最大为7

算法实现：

python 复制代码

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def rob(root):
    """
    树形动态规划解法
    时间复杂度: O(n)，n为节点数
    空间复杂度: O(h)，h为树高
    
    状态定义: 返回一个元组 (rob_current, not_rob_current)
            rob_current: 偷当前节点的最大收益
            not_rob_current: 不偷当前节点的最大收益
    """
    def dfs(node):
        if not node:
            return (0, 0)  # (偷当前节点的最大值，不偷当前节点的最大值)
        
        # 后序遍历：先处理子节点
        left = dfs(node.left)
        right = dfs(node.right)
        
        # 偷当前节点，则不能偷子节点
        rob_current = node.val + left[1] + right[1]
        
        # 不偷当前节点，子节点可偷可不偷（取最大值）
        not_rob_current = max(left[0], left[1]) + max(right[0], right[1])
        
        return (rob_current, not_rob_current)
    
    result = dfs(root)
    return max(result[0], result[1])

# 测试
root = TreeNode(3)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.right = TreeNode(3)
root.right.right = TreeNode(1)
print(rob(root))  # 输出: 7

5. 旅行商问题 (Traveling Salesman Problem, TSP)

问题描述：

一个旅行商人需要访问 n 个城市，每个城市恰好访问一次，最后回到起点。已知每两个城市之间的距离，求最短的旅行路线。这是一个经典的NP-hard问题。

示例：

复制代码

4个城市，距离矩阵:
[
  [0, 10, 15, 20],
  [10, 0, 35, 25],
  [15, 35, 0, 30],
  [20, 25, 30, 0]
]

最短路径: 0 -> 1 -> 3 -> 2 -> 0
路径长度: 10 + 25 + 30 + 15 = 80

算法实现：

python 复制代码

def tsp(dist):
    """
    旅行商问题 - 状态压缩动态规划解法
    时间复杂度: O(n² * 2^n)，适合小规模问题（n ≤ 20）
    空间复杂度: O(n * 2^n)
    
    状态定义: dp[mask][i] 表示从城市0出发，经过mask中的城市集合，最后到达城市i的最短路径
            mask: 用二进制表示已访问的城市集合（1表示已访问，0表示未访问）
    """
    n = len(dist)
    
    # dp[mask][i]: 从起点0出发，经过mask中的城市，最后到达i的最小距离
    dp = [[float('inf')] * n for _ in range(1 << n)]
    dp[1][0] = 0  # 初始状态：只访问了城市0，当前位置在城市0
    
    # 遍历所有状态
    for mask in range(1 << n):
        for i in range(n):
            # 如果当前状态不可达，跳过
            if dp[mask][i] == float('inf'):
                continue
            
            # 尝试访问下一个未访问的城市j
            for j in range(n):
                if not (mask >> j) & 1:  # 如果城市j未访问
                    new_mask = mask | (1 << j)
                    dp[new_mask][j] = min(dp[new_mask][j], 
                                         dp[mask][i] + dist[i][j])
    
    # 找到回到起点的最短路径
    result = float('inf')
    final_mask = (1 << n) - 1  # 所有城市都已访问
    
    for i in range(1, n):  # 从任意非起点城市回到起点
        if dp[final_mask][i] + dist[i][0] < result:
            result = dp[final_mask][i] + dist[i][0]
    
    return result

# 测试
dist = [
    [0, 10, 15, 20],
    [10, 0, 35, 25],
    [15, 35, 0, 30],
    [20, 25, 30, 0]
]
print(tsp(dist))  # 输出: 80

6. 编辑距离 (Edit Distance) - LeetCode 72

问题描述：

给定两个单词 word1 和 word2，计算将 word1 转换成 word2 所需的最少操作次数。允许的操作有三种：

插入一个字符
删除一个字符
替换一个字符

示例：

复制代码

输入: word1 = "horse", word2 = "ros"
输出: 3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

算法实现：

python 复制代码

def minDistance(word1, word2):
    """
    编辑距离动态规划解法
    时间复杂度: O(m×n)
    空间复杂度: O(m×n)，可优化到O(min(m, n))
    
    状态定义: dp[i][j] 表示 word1[0:i] 转换为 word2[0:j] 的最小编辑距离
    状态转移:
        1. 如果 word1[i-1] == word2[j-1]: dp[i][j] = dp[i-1][j-1]
        2. 否则: dp[i][j] = min(
                dp[i-1][j] + 1,      # 删除 word1[i-1]
                dp[i][j-1] + 1,      # 插入 word2[j-1]
                dp[i-1][j-1] + 1     # 替换 word1[i-1] 为 word2[j-1]
            )
    """
    m, n = len(word1), len(word2)
    
    # 初始化dp数组
    dp = [[0] * (n + 1) for _ in range(m + 1)]
    
    # 边界条件初始化
    for i in range(m + 1):
        dp[i][0] = i  # 将word1[0:i]转换为空字符串需要i次删除
    for j in range(n + 1):
        dp[0][j] = j  # 将空字符串转换为word2[0:j]需要j次插入
    
    # 填充dp表
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if word1[i-1] == word2[j-1]:
                dp[i][j] = dp[i-1][j-1]
            else:
                dp[i][j] = min(
                    dp[i-1][j] + 1,      # 删除
                    dp[i][j-1] + 1,      # 插入
                    dp[i-1][j-1] + 1     # 替换
                )
    
    return dp[m][n]

# 测试
print(minDistance("horse", "ros"))  # 输出: 3
print(minDistance("intention", "execution"))  # 输出: 5

四、动态规划解题模板

通用解题步骤：

定义状态：dp数组的含义要明确
确定转移方程：状态之间的关系
初始化：边界条件的处理
确定遍历顺序：保证计算当前状态时子状态已计算
输出结果：最终答案在dp数组中的位置

记忆化搜索模板：

python 复制代码

def memoization_template(n):
    memo = {}  # 存储已计算的结果
    
    def dfs(state):
        # 1. 边界条件
        if state in memo:
            return memo[state]
        
        # 2. 递归终止条件
        if is_base_case(state):
            return base_value
        
        # 3. 状态转移
        result = some_operation(dfs(next_state1), dfs(next_state2), ...)
        
        # 4. 记忆化
        memo[state] = result
        return result
    
    return dfs(initial_state)