大学院-筆記試験練習:线性代数和数据结构(7)
- 1-前言
- 2-线性代数-题目
- 3-线性代数-参考答案
- 4-数据结构-题目
- 5-数据结构-参考答案
- 問1 【満点】
- 問2 【满点】
- 問3 ⚠️【立命馆会扣分的地方在这里】⚠️
-
- [(1) 最初に衝突が起きる要素](#(1) 最初に衝突が起きる要素)
- [(2) ハッシュ表の内容 ❌【这里是主要失分点】](#(2) ハッシュ表の内容 ❌【这里是主要失分点】)
-
- [❌ 根本性错误](#❌ 根本性错误)
- [❗ 立命馆这里是「理解检查点」](#❗ 立命馆这里是「理解检查点」)
- 正确答案应该是(线性探索):
- [(3) 最悪時間計算量](#(3) 最悪時間計算量)
- 最终评分预测(按立命馆)
- 给你一句「立命馆必背」
- 6-总结
1-前言
为了升到自己目标的大学院,所作的努力和学习,这里是线性代数和数据结构部分。
2-线性代数-题目

3-线性代数-参考答案

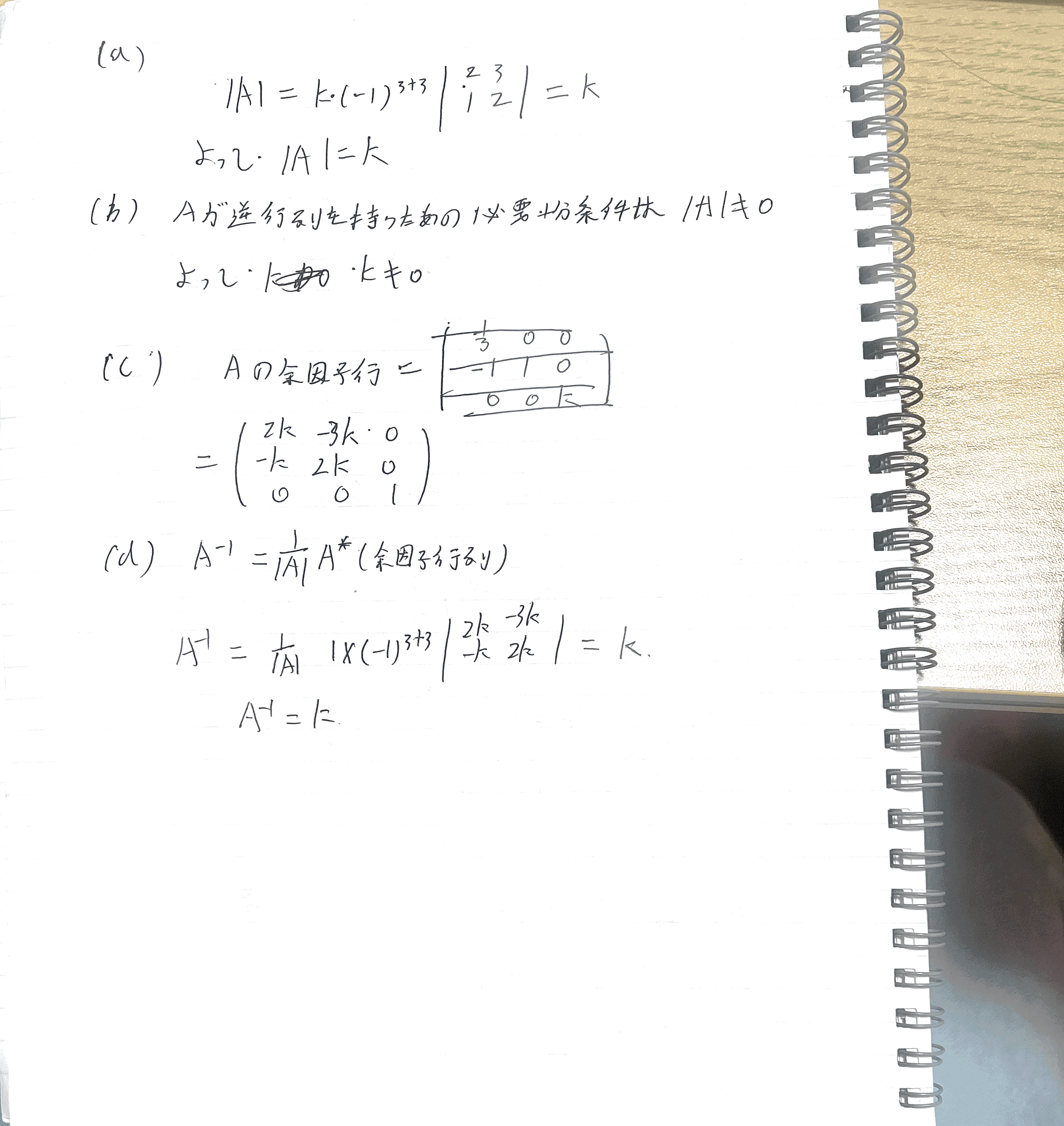

4-数据结构-题目
問1(連結リストと計算量)【相似題①】
要素数 (n) の単方向連結リストを考える。
各ノードは val と next を持つものとする。
次の 実装方法 A・B が与えられている。
-
実装方法 A :
先頭要素のアドレスのみを
headが保持する。 -
実装方法 B :
先頭要素のアドレスを
head,末尾要素のアドレスをtailが保持する。
(1)
実装方法 B において,
「末尾への要素追加」と「先頭要素の削除」を繰り返すとき,
このデータ構造の名称を 1 つ答えよ。
(2)
実装方法 A,B それぞれについて,
末尾要素を探索して値を参照する操作 の最悪時間計算量を,
要素数 (n) を用いてオーダー記法で答えよ。
(3)
実装方法 A において,
先頭から (k) 番目の要素を削除する場合の最悪時間計算量を,
(n) と (k) を用いて答えよ。
問2(ソートアルゴリズムの性質)【相似題②】
(1)
最悪時間計算量が (O(n^2)) であり,安定である。
(2)
最悪時間計算量が (O(n \log n)) であり,安定である。
(3)
平均時間計算量が (O(n \log n)) であり,不安定である。
※ 安定とは,等しい値を持つ要素の相対的な順序が
ソート前後で保存されることをいう。
問3(予測出題:ハッシュ法)【予測題】
データ集合
S = {12,\\ 7,\\ 18,\\ 3,\\ 14,\\ 9,\\ 21}
をこの順に挿入する。
ハッシュ関数を
h(x) = x \\bmod 5
とし,衝突解決法として線形探索法(オープンアドレス法) を用いる。
(1)
最初に衝突が発生する要素の値を答えよ。
(2)
すべての要素を挿入した後のハッシュ表の内容を,
添字 0 から順に 示せ。
(3)
この探索方法における,
探索成功時の最悪時間計算量を
要素数 (n) を用いてオーダー記法で答えよ。
5-数据结构-参考答案

問1 【満点】
(1)
キュー(FIFO)
✅ 完全正确
- 「末尾追加+先頭削除」= Queue
- FIFO 写不写都不影响得分
(2)
実装A:O(n)
実装B:O(1)
✅ 完全正确
- A:只有 head → 需要遍历
- B:有 tail → 直接参照
(3)
O(n)
✅ 完全正确
- 删除第 k 个元素
- 需要从 head 找到第 k−1 个节点
- 最坏情况 k≈n
👉 問1 满点
問2 【满点】
(1)
バブルソート,挿入ソート
✅ 正确
- O(n²)
- 稳定
- ✔ 选择排序被你划掉是对的(不稳定)
(2)
マージソート
✅ 正确
- O(n log n)
- 稳定
(3)
ヒープソート
✅ 正确
- 平均 O(n log n)
- 不稳定
👉 問2 满点
問3 ⚠️【立命馆会扣分的地方在这里】⚠️
(1) 最初に衝突が起きる要素
你的答案:
h(12)=2
h(7)=2
よって 7
✅ 结论是正确的
❌ 但理由写法不严谨
立命馆标准要求的是:
「先に格納されている要素と同じハッシュ値を持つ最初の要素」
你没有明确写"插入顺序"导致冲突 ,
严格来说是:
- 12 先入 → 占用 index 2
- 7 后入 → index 2 冲突
📌 本番会小扣 1〜2 分
(2) ハッシュ表の内容 ❌【这里是主要失分点】
❌ 根本性错误
你画的是:
👉 链地址法(連結リスト法 / chaining)
但题目是:
線形探索法(オープンアドレス法)
❗ 立命馆这里是「理解检查点」
| 方法 | 是否允许链表 |
|---|---|
| オープンアドレス法 | ❌ 不允许 |
| 連結法 | ✅ 允许 |
👉 你的画法 = 方法错误
正确答案应该是(线性探索):
插入顺序:
| 元素 | h(x) | 实际位置 |
|---|---|---|
| 12 | 2 | 2 |
| 7 | 2 | 3 |
| 18 | 3 | 4 |
| 3 | 3 | 0 |
| 14 | 4 | 1 |
| 9 | 4 | ❌ 表满前继续 |
| 21 | 1 | ❌ |
👉 标准写法(例):
index: 0 1 2 3 4
value: 3 14 12 7 18📌 这里立命馆会扣 5〜8 分
(3) 最悪時間計算量
你的答案:
O(n)
✅ 正确
- 线性探索
- 最坏全部探查
最终评分预测(按立命馆)
| 问题 | 结果 |
|---|---|
| 問1 | ◎ |
| 問2 | ◎ |
| 問3(1) | ○(轻微减点) |
| 問3(2) | ❌(方法错误) |
| 問3(3) | ◎ |
👉 整体:合格线以上,但不是安全满分
给你一句「立命馆必背」
「オープンアドレス法では,
1 つの添字には 1 要素のみ格納される。」
这一句写在脑子里 ,
以后 哈希题 0 失误。
6-总结
训练成长。!!