冗余连接II - 技术栈

本文参考代码随想录

在本问题中，有根树指满足以下条件的有向图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。

输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组 edges 。每个元素是一对 $ui, vi$ ，用以表示有向图中连接顶点 ui 和顶点 vi 的边，其中 ui 是 vi 的一个父节点。

返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

思路

有如下三种情况，前两种情况是出现入度为2的点，

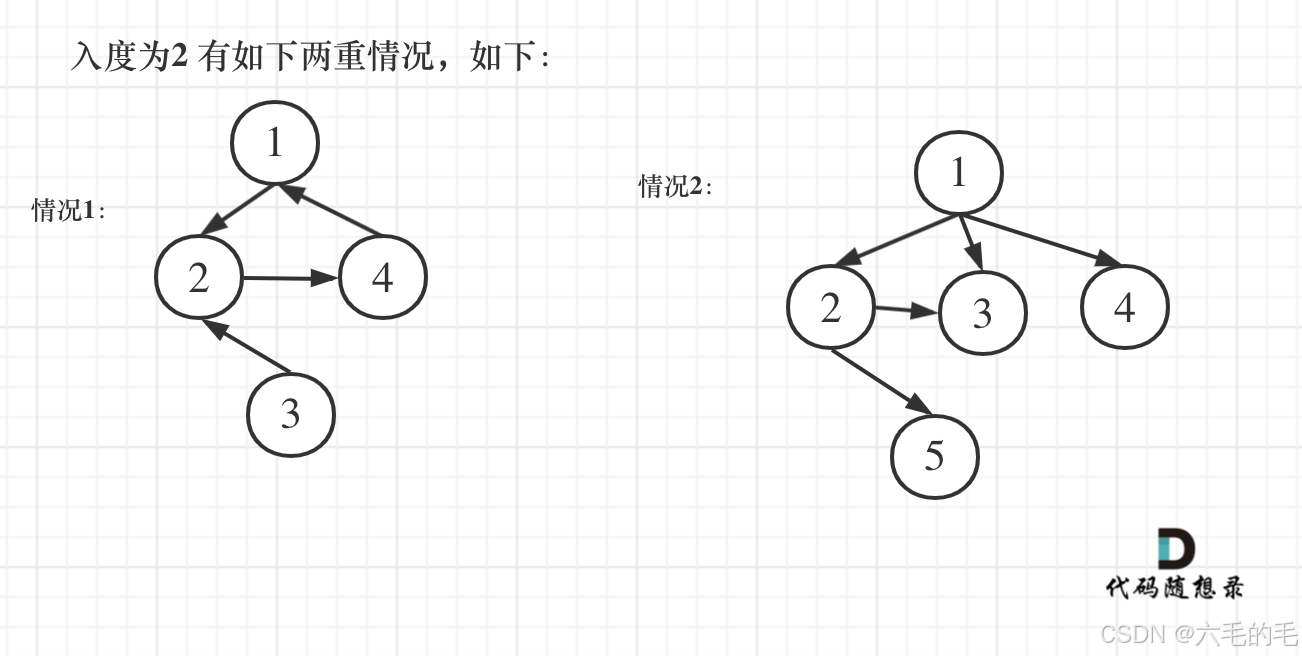
第三种情况是没有入度为2的点，那么图中一定出现了有向环

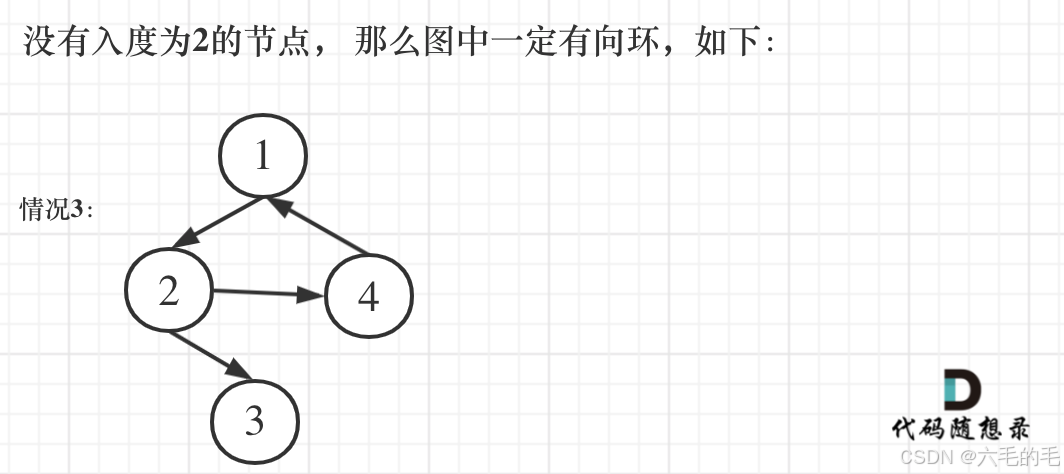
python 复制代码

class Solution:
    def init(self, n):
        self.fathers = [i for i in range(n + 1)]
    def find(self, u):
        if self.fathers[u] == u:
            return u
        self.fathers[u] = self.find(self.fathers[u])
        return self.fathers[u]
    def isSame(self, u, v):
        return self.find(u) == self.find(v)

    def join(self, u, v):
        # u -> v
        u = self.find(u)
        v = self.find(v)
        if u == v:
            return
        self.fathers[v] = u

    def isTreeAfterRemove(self, edge, edges):
        self.init(len(edges) + 1)
        for e in edges:
            if e == edge:
                continue
            if self.isSame(e[0], e[1]):
                return False
            self.join(e[0], e[1])
        return True
    
    def removeCircleEdge(self, edges):
        self.init(len(edges) + 1)
        for e in edges:
            if self.isSame(e[0], e[1]):
                return e
            self.join(e[0], e[1])

    def findRedundantDirectedConnection(self, edges: List[List[int]]) -> List[int]:
        inDegrees = [0] * (len(edges) + 1)
        twoDegreeVecs = []
        for e in edges:
            inDegrees[e[1]] += 1
        for e in edges:
            if inDegrees[e[1]] == 2:
                twoDegreeVecs.append(e)
        if len(twoDegreeVecs) > 0:
            for e in twoDegreeVecs[::-1]:
                if self.isTreeAfterRemove(e, edges):
                    return e
        return self.removeCircleEdge(edges)