2026.1.11力扣刷题笔记

题目：

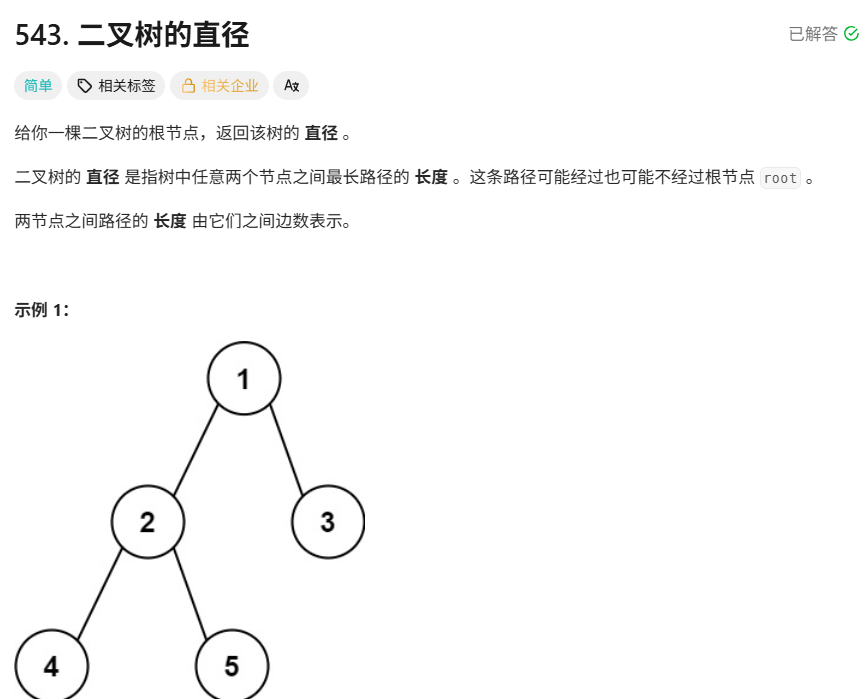
解答：

cpp 复制代码

int deep(struct TreeNode* root,int* dist){
    if(root==NULL)
        return 0;
    int left_level=deep(root->left,dist);
    int right_level=deep(root->right,dist);
    if(left_level+right_level>*dist)//key步骤
        *dist=left_level+right_level;     
    if (left_level >= right_level)
        left_level++;
    else
        right_level++;
    int max;
    max=(left_level>=right_level)?left_level:right_level;
    return max;
}
int diameterOfBinaryTree(struct TreeNode* root) {
    int dist=0;
    deep(root,&dist);
    return dist;
}

心得：原思路想的是直接root节点的左子树深度加上右子树深度就能得到最大深度，但是测试样例有五个过不了。后面看大佬的想到可能出现子树中出现最大dist，就定义一个参数记录每个结点的最大深度，最后返回全树的最大深度。

题目：

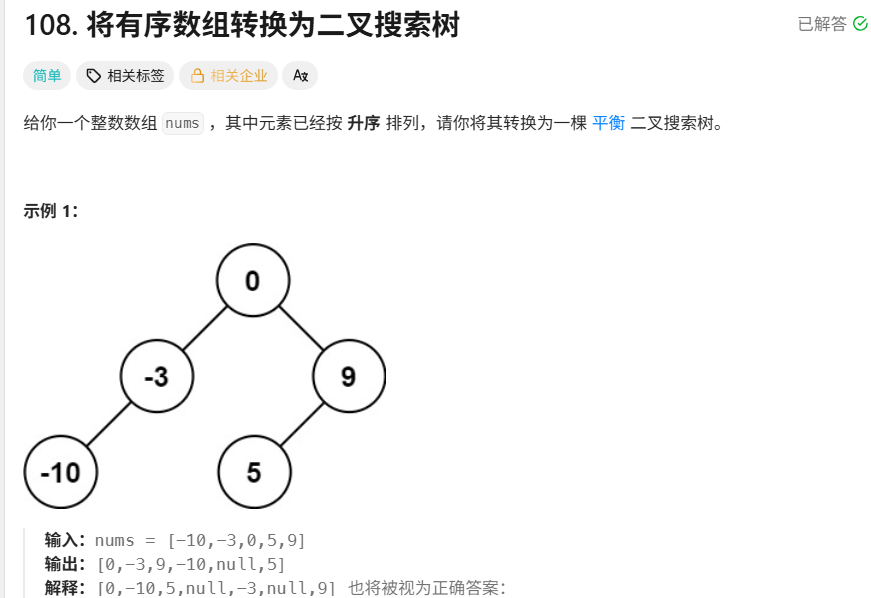
解答：

cpp 复制代码

struct TreeNode* buildtree(int* nums,int left,int right){
    if (left > right) {
        return NULL;
    }
    int mid=(left+right)/2;
    struct TreeNode* root=(struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->val=nums[mid];
    root->left=buildtree(nums,left,mid-1);
    root->right=buildtree(nums,mid+1,right);
    return root;
}
struct TreeNode* sortedArrayToBST(int* nums, int numsSize) {
        return buildtree(nums,0,numsSize-1);
}

心得：题目要求就是将数组转化为构建一颗平衡树，所以很容易想到使用折半的方法，每次使用mid作为根节点进行递归，但需要注意递归的结束条件设定以及创建根节点等细节处理。

题目：

解答：

cpp 复制代码

int searchInsert(int* nums, int numsSize, int target) {
    if(target<nums[0])
        return 0;
    if(target>nums[numsSize-1])
        return numsSize;
    int left=0,right=numsSize-1;
    int mid;
    while(left<=right){
        mid=(right+left)/2;
        if(nums[mid]==target)
            return mid;
        else if(nums[mid]<target)
            left=mid+1;
        else
            right=mid-1;
    }
    return left;
}

心得：折半查找，找到之后返回mid的下标；没找到时，总是返回left指针指向的值，该值始终大于当前mid值。