【题目描述】
Alice和Bob玩了一个古老的游戏:首先画一个n × n的点阵(下图n = 3)
接着,他们两个轮流在相邻的点之间画上红边和蓝边:
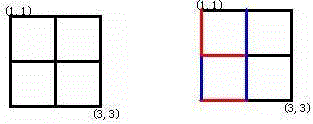
直到围成一个封闭的圈(面积不必为1)为止,"封圈"的那个人就是赢家。因为棋盘实在是太大了(n ≤ 200),他们的游戏实在是太长了!他们甚至在游戏中都不知道谁赢得了游戏。于是请你写一个程序,帮助他们计算他们是否结束了游戏?
【输入】
输入数据第一行为两个整数n和m。m表示一共画了m条线。以后m行,每行首先有两个数字(x, y),代表了画线的起点坐标,接着用空格隔开一个字符,假如字符是"D ",则是向下连一条边,如果是"R "就是向右连一条边。输入数据不会有重复的边且保证正确。
【输出】
输出一行:在第几步的时候结束。假如m步之后也没有结束,则输出一行"draw"。
【输入样例】
3 5
1 1 D
1 1 R
1 2 D
2 1 R
2 2 D【输出样例】
41. 题目背景与算法模型
核心问题:在一个N*N的网格图中,判断哪一步连边操作后首次形成环。
算法模型:连通性维护与判环,首选并查集。
2. 解法一:基于 STL 的直接存储法 (Map + Pair)
此方法无需推导坐标映射公式,适合处理稀疏图或非标准网格
完整代码
cpp
//这道题首先应想到当画一条边前如果find(u)==find(v)了,那么这条边一画
//就成环了,就结束游戏了,然后就是想着如何存坐标 两种方式
//第一种直接用pair或者结构体struct自己写一个pair然后存入map,但是map是会对键自动排序的
//所以如果用pair就不用管,因为pair会按照字典序自动排序,但如果自己写结构体 就要重载一下运算符
//第二种直接把二维坐标转换成一维数字,把每一个坐标都用一个数字替换
//pair写法
#include <bits/stdc++.h>
#include <algorithm>
#include <map>
using namespace std;
int n,m;
//定义类型别名,避免后续反复书写pair<int,int>
typedef pair<int,int> pii;
pii p1;
pii p2;
map<pii,pii> fa;//fa存每个坐标的父/祖先节点
pii find(pii x){
if(fa[x]==x) return x;//如果已经是祖先/根结点 返回
//否则就递归找祖先 并进行路径压缩
return fa[x]=find(fa[x]);
}
void uni(pii x,pii y){
pii fax=find(x);//x的祖先节点
pii fay=find(y);//y的祖先节点
//如果相等说明在一个集合 无事发生,不相等就让fax成为fay的老大的老大
if(fax!=fay){
fa[fay]=fax;
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int x,y;
char c;
cin>>x>>y>>c;
p1={x,y};
if(c=='D')//向下
p2={x+1,y};
else//向右
p2={x,y+1};
//如果p1 p2还没有父节点,就初始化父节点为自己
if(!fa.count(p1)) fa[p1]=p1;
if(!fa.count(p2)) fa[p2]=p2;
//当画一条边前如果find(u)已经==find(v)了,那么这条边一画 就成环了
if(find(p1)==find(p2)){
cout<<i;
return 0;
}
uni(p1,p2);
}
cout<<"draw";
return 0;
}3. 解法二:二维坐标转化为一位标记的数组法
这是竞赛中的标准解法,通过ID = (x-1)*N+y将二维坐标映射为一维,效率最高。
cpp
//第二种方法二维坐标用一维数字代替,节省大量代码
#include <bits/stdc++.h>
using namespace std;
int n,m;
int fa[40010];
//二维坐标压缩成一维标记
int getid(int x,int y){
return (x-1)*n+y;
}
int find(int x){
if(fa[x]==x) return x;//如果已经是祖先/根结点 返回
//否则就递归找祖先 并进行路径压缩
return fa[x]=find(fa[x]);
}
void uni(int x,int y){
int fax=find(x);//x的祖先节点
int fay=find(y);//y的祖先节点
//如果相等说明在一个集合 无事发生,不相等就让fax成为fay的老大的老大
if(fax!=fay){
fa[fay]=fax;
}
}
int main(){
cin>>n>>m;
//初始化自己的祖先为自己
for(int i=1;i<=n*n;i++) fa[i]=i;
for(int i=1;i<=m;i++){
int x,y;
char c;
cin>>x>>y>>c;
int p1=getid(x,y);
int p2=-1;
if(c=='D')//向下
p2=getid(x+1,y);
else//向右
p2=getid(x,y+1);
//如果p1 p2还没有父节点,就初始化父节点为自己
//当画一条边前如果find(u)已经==find(v)了,那么这条边一画 就成环了
if(find(p1)==find(p2)){
cout<<i;
return 0;
}
uni(p1,p2);
}
cout<<"draw";
return 0;
}4. 关键复盘:STL 写法中的严重易错点
在使用第一种方法(Map + Pair)时,许多同学会因为不熟悉 C++ 强类型机制而遭遇编译错误或逻辑异常。以下是必须规避的三个核心错误:
易错点 1:错误使用 Pair 作为类型名会导致信息学奥赛一本通system error
这是新手最容易犯的语法错误。
-
错误写法:
pair p1; // ❌ 错误:缺少模板参数 pair find(pair x) { // ❌ 错误:编译器无法推断 pair 内部存什么 ... } -
错误原因 :
std::pair本质上是一个类模板 ,而非具体的类型 (Type) 。它就像一个模具,必须明确告诉编译器里面装的是int、double还是string,编译器才能生成具体的代码。 -
正确写法:必须显式指定模板参数。
cpppair<int,int> p1; // ✅ 正确 pair<int,int> find(pair<int,int> x) { ... } // ✅ 正确 -
优化建议 :使用
typedef或using简化代码。cpptypedef pair<int,int> pii; pii find(pii x) { ... }
易错点 2:Map 的自动构造陷阱
-
错误现象 :没有对 map 进行初始化,直接在
find函数中访问fa[x]。 -
后果 :当访问不存在的键时,
std::map会自动插入该键,并将其值初始化为默认值({0,0})。这会导致所有未手动初始化的节点,其父节点都被错误地指向{0,0},破坏并查集的树形结构。 -
修正方案 :在调用
find前,必须使用if(!fa.count(p))检查并手动初始化fa[p] = p;。
易错点 3:并查集路径压缩的浅拷贝问题
-
错误写法 :
void uni(pii x,pii y) {fa[y]=fa[x];} -
分析 :这行代码并没有去寻找
x和y的根节点(祖宗),仅仅是将y的父节点修改了。这在路径压缩未完成时是错误的,会导致集合无法正确合并。 -
正确写法 :必须调用
find函数获取根节点。cpppii fax=find(x); pii fay=find(y); if(fax!=fay) fa[fay]=fax;
5. 总结
本题通过两种解法展示了数据结构选择的权衡:
-
数组法 :利用数学映射实现O(1)访问,是处理标准网格图的最优解。
-
STL 法 :代码逻辑直观,但要求对C++ 模板语法 和容器机制有一定理解,否则极易出现编译错误或隐蔽的运行时错误。